README.md

An expedition ☛『Discrete Mathematics』in『Geometric Optics』

About

• This dive 👉 『Geometric optics』in『Discrete mathematics』
  1. Described by .ppt ⊊ 👉「1.『Multiple Euclidean algorithm』runs automatically in『Dewar bottle』=『pure-reflection non-absorbing notched blackbody』.pptx」
  2. Utilizes simulator ⊷ 👉 2D ray-optics simulation
     • Utilized by .ppt ⊶ 👉「A_guided_tour_to_Ray_&_Wave_Optics_Simulation.pptx」
       • Links to model ✉ 👉 NLAST-vector model (Private)
         • Contains paper ⊋ 👉 Berry-Mcleod paper (Private)
         • 『Wave Optics』in『Partial Differential Equations (PDEs)』
  3. Involved in book ⊊ 👉 Illusions_of_Illustrations_·_Zodiac
     • Contained by books ⊂ 👉 three e-books
  4. Belongs to Career ⊊ 👉 PhD activities
  5. Linked to ✉ 👉「Penrose's room」that「cannot be illuminated by a single point」
• 中文「自述文档」㊥ 👉 几何光学 in 离散数学

Description

• 『This exploration process』is one of『the examples of the second book』
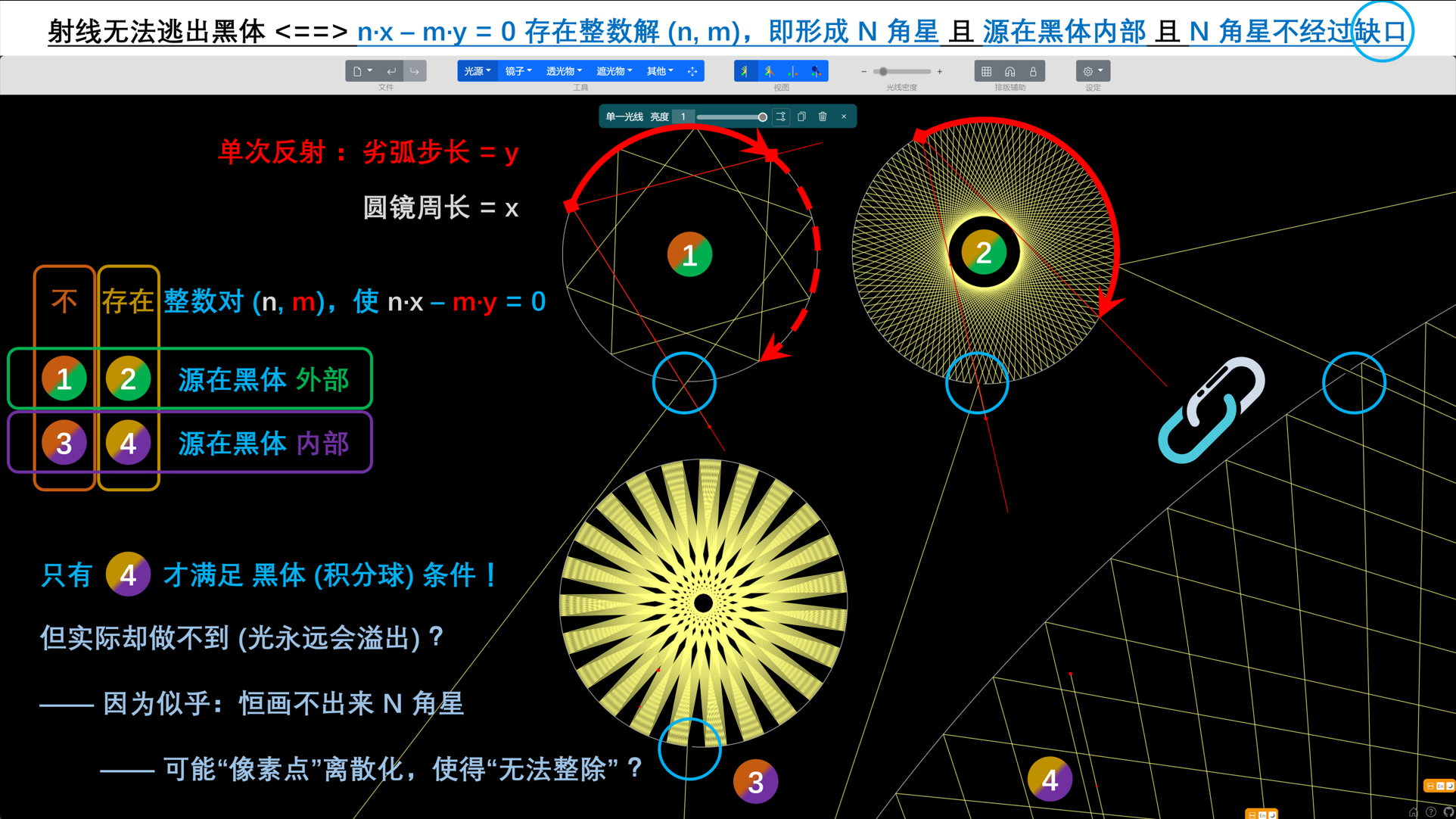
  • Using『Euclidean algorithm』to understand the『Multiple reflections』of light from the『Inner wall of the silver mirror』in the unsealed『Dewar bottle』
• Discussed the application of algebra (mathematics) in geometry (optics)
  • External light source: when it enters the『pure reflection blackbody』from the outside, the light will eventually come out from the gap. Why?
  • Internal light source: when the source is inside the『pure reflection blackbody』,light may not necessarily come out from the gap. What are the corresponding conditions?

Inplementation

1. Ideological perspective: Abstract the『optical process』in『concave mirror』into『mathematical process』
   • See the animation in file「Multiple Euclidean algorithm runs automatically in『Dewar bottle』=『pure-reflection non-absorbing notched blackbody』.pptx」
   • See the content『The origin of the circular vector』on page 8 of「2.『Illusions_of_Illustrations_·_Zodiac』.pdf」
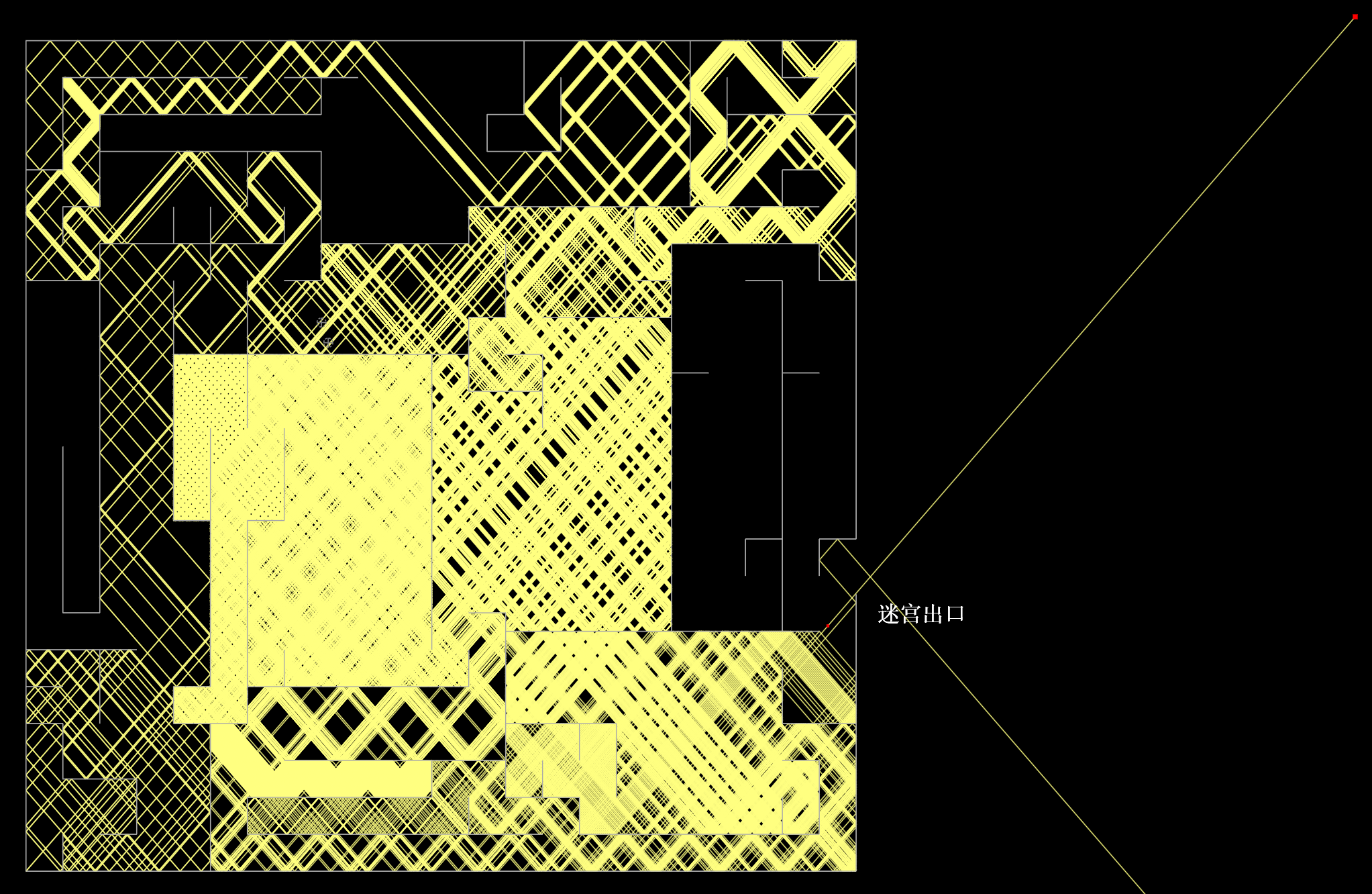
2. Optical Expansion:『Integral Sphere with Notches』➞『Maze with Exits』
   • The same conclusion applies to『any other shape』, such as a『labyrinth-shaped cavity』
   • That is to say, the shape of a blackbody may not necessarily be spherical
     • If the light source is『inside the maze』, the light『may not be able to solve/escape the maze』
     • See the case『Maze solution』
     • If the light source is『outside the maze』, then the light『can definitely come out of the maze again』
     • 
     • 
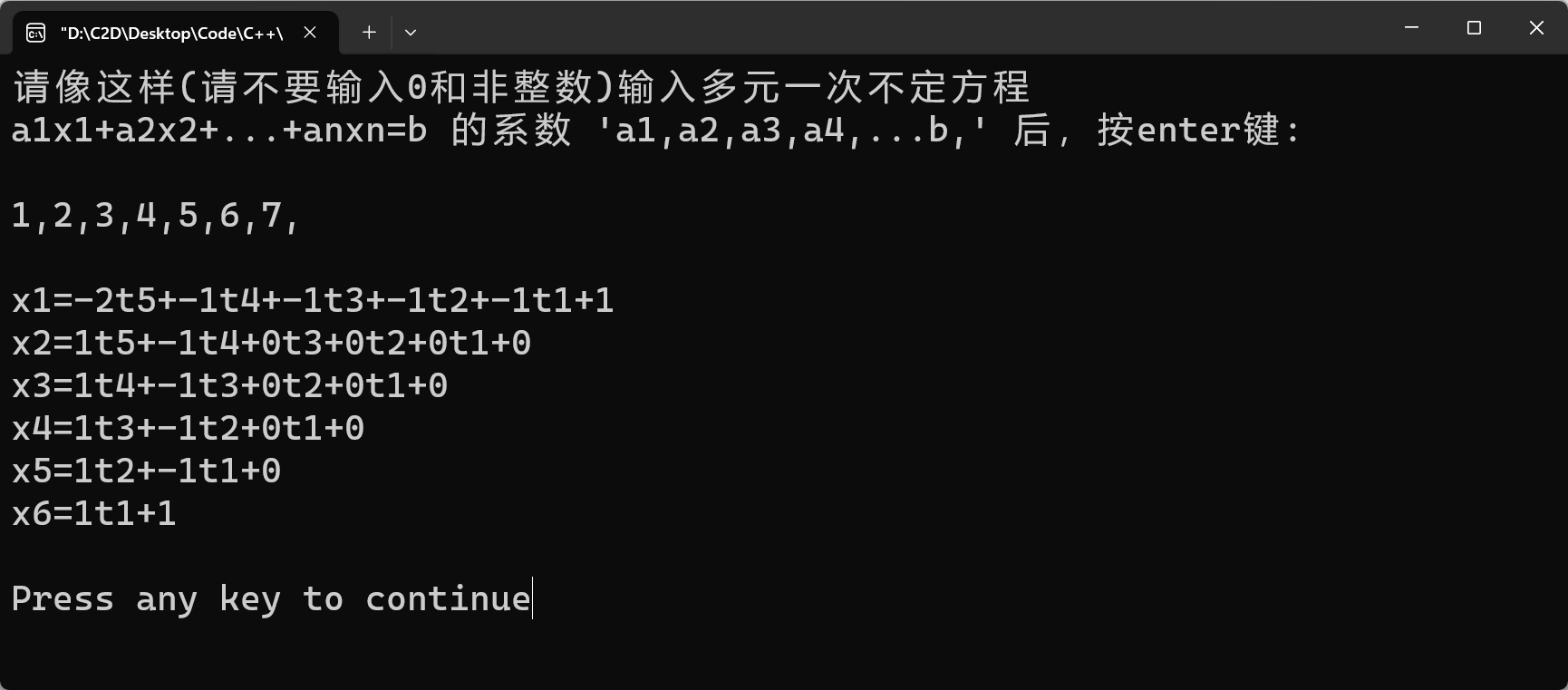
3. Mathematical Expansion:『Bivariate』to『Multivariate』linear indeterminate equation ('s Special/General solution)
   • Open the folder "cpp_codes_for_book2『Illusions_of_Illustrations_·_Zodiac』".
   • Run「12.第10个程序的改良版(2+5+8b).cpp」inside using Visual C++ 6.0, or rather,
     • using Microsoft Visual Studio C++ 6.0\Common\MSDev98\Bin\MSDEV.EXE.
     • VC6.0 Download & Setup ; Higher version of C++ is recommended, but may not be able to run this project?
   • 
   • See page 10 of「2.『Illusions_of_Illustrations_·_Zodiac』.pdf」

History

• This dive 👉 『Geometric optics』in『Discrete mathematics』
  • (Personal time) 25-year_10-month-old
  • (Personal stage) Ph.D. 2nd Grade Winter Vacation (1.5 / 3.0)
  • (World time) 2024.02