二进制 & 位运算.md

# 二进制 / 位运算

----

![二进制位运算](https://img-blog.csdnimg.cn/20191021201855750.png)

```css
优点：

特定情况下，计算方便，速度快，被支持面广
如果用算数方法，速度慢，逻辑复杂
位运算不限于一种语言，它是计算机的基本运算方法
```

<br>

## 知识点预热

----

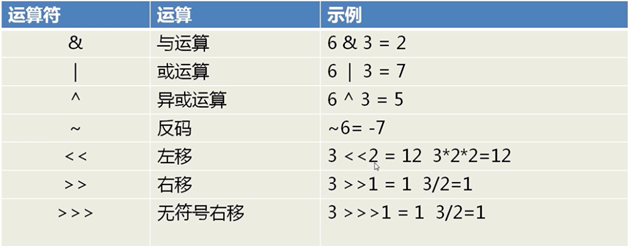
#### （一）按位与&
两位`全为1`，结果才为1

0&0=0；0&1=0；1&0=0；1&1=1

`例如`：51&5 即 `0011 0011` & `0000 0101` =`0000 0001` 因此51&5=1.

特殊用法

（1）`清零`。如果想将一个单元清零，即使其全部二进制位为0，只要与一个各位都是零的数值相与，结果为零。

（2）取一个数中`指定位`。

例如：设 X=10101110，取X的`低四位`，用`X`&`0000 1111`=`0000 1110`即可得到。

`方法`：找一个数，对应x要取的位，该数的对应位为1，其余位为零，此数与x进行“与运算”可以得到x中的指定位。

#### （二）按位或 |
`只要有一个`为1，结果就为1。

0|0=0； 0|1=1；`1|0=1`；1|1=1；

例如：51|5 即`0011 0011` | `0000 0101` =`0011 0111` 因此51|5=55

 特殊用法

常用来对一个数据的某些位置1。

`方法`：找到一个数，对应x要置1的位，该数的对应位为1，其余位为零。此数与x相或可使x中的某些位置1。

#### （三）异或 ^
两个相应位`为“异”（值不同）`，则该位结果为1，否则为0

0^0=0;  `0^1=1`; 1^0=1; 1^1=0;

`例如`：51^5 即`0011 0011` ^ `0000 0101` =`0011 0110` 因此51^5=54

特殊用法

（1）  `与1`相异或，使特定位`翻转`

方法：找一个数，对应X要翻转的位，该数的对应为1，其余位为零，此数与X对应位异或即可。

例如：X=1010 1110，使X低四位翻转，用X^0000 1111=1010 0001即可得到。

（2）  `与0`相异或，保留`原值`

例如：X^0000 0000 =1010 1110

（3）两个变量`交换值`

1.借助第三个变量来实现

C=A;A=B;B=C;

2.利用加减法实现两个变量的交换

 A=A+B;B=A-B;A=A-B;

3.用位异或运算来实现，也是效率最高的

原理：一个数异或本身等于0 ；异或运算符合交换律

`A=A^B`;`B=A^B`;`A=A^B`

#### （四）取反与运算~
对一个二进制数按位取反，即将0变为1，1变0

```css
~1=0 ；~0=1
```

#### （五）左移<<
将一个运算对象的各二进制位全部`左移若干位`（左边的二进制位丢弃，右边补0）

`例如`： 2<<1 =4    10<<1=100

若左移时舍弃的高位`不包含1`，则每`左移`一位，相当于该数`乘以2`。

例如：

       11(1011)<<2= 0010 1100=22

       11(00000000 00000000 00000000 1011)整形32bit

#### （六）右移>>
将一个数的各二进制位全部`右移`若干位，`正数`左补0，`负数`左补1，`右边丢弃`。若右移时舍`高位不是1`（即不是负数），操作数每`右移`一位，相当于该数`除以2`。

左补0还是补1得看被移数是正还是负。

例如：`4>>2=4/2/2=1`

        -14（即1111 0010）>>2 =1111 1100=-4

#### （七）无符号右移运算>>>
各个位向`右移指定的位数`，右移后左边`空出的位用零`来填充，移除`右边的位被丢弃`。

`例如`：-14>>>2

（即`11111111 11111111 11111111 11110010`）>>>2

=(`00111111 11111111 11111111 11111100`)=1073741820



![在这里插入图片描述](https://img-blog.csdnimg.cn/20191021202057416.png)

<br>
<br>

## 只出现一次的数字

----

给出 `2 * n + 1`个数字，除其中一个数字之外其他每个数字均出现两次，找到这个数字。

异或运算具有很好的性质，相同数字异或运算后为0，并且具有交换律和结合律，故将所有数字异或运算后即可得到只出现一次的数字。

示例 :

```css
输入: [4,1,2,1,2]
输出: 4
```

#### 解题思路

如果我们对 0 和二进制位做 XOR 运算，得到的仍然是这个二进制位

$a \oplus 0 = a$ $a⊕0=a$

如果我们对相同的二进制位做 XOR 运算，返回的结果是 0

$a \oplus a = 0$ $a⊕a=0$

XOR 满足交换律和结合律

$a \oplus b \oplus a = (a \oplus a) \oplus b = 0 \oplus b = ba⊕b⊕a=(a⊕a)⊕b=0⊕b=b$

所以我们只需要将`所有`的数进行 XOR 操作，得到那个唯一的数字。

```java
public int singleNumber(int[] A) {
    if(A == null || A.length == 0) {
        return -1;
    }
    int rst = 0;
    for (int i = 0; i < A.length; i++) {
        rst ^= A[i];
    }
    return rst;
}
```

#### 复杂度分析

时间复杂度： `O(n)` 。我们只需要将 $\text{nums}$ 中的元素遍历一遍，所以时间复杂度就是 $\text{nums}$ 中的元素个数。
空间复杂度：`O(1)` 。


<br>
<br>

## 格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个二进制的差异。给定一个`非负整数 n` ，表示该代码中所有二进制的总数，请找出其格雷编码顺序。一个格雷编码顺序必须以 `0` 开始，并覆盖所有的 `2n` 个整数。例子——输入：`2`；输出：[0, 1, 3, 2]；解释: `0 - 00`，`1 - 01`，`3 - 11`，`2 - 10`

#### 解题思路

格雷码生成公式：`G(i) = i ^ (i >> 2)`

```css
public ArrayList<Integer> grayCode(int n) {
    ArrayList<Integer> result = new ArrayList<Integer>();
    for (int i = 0; i < (1 << n); i++) {
        result.add(i ^ (i >> 1));
    }
    return result;
}
```

<br>
<br>