Skip to content

Latest commit

 

History

History
117 lines (92 loc) · 6.31 KB

README.md

File metadata and controls

117 lines (92 loc) · 6.31 KB
Raw

Go-L

Game of Life simulation

I originally wrote a Game of Life model in C, GOL. But I wanted to convert it into Golang for a few reasons:

  • Learn Go
  • Consider more novel topologies based on border rules (see #border-topologies).
  • Extend GOL simulation for generic update rules.
  • Extend GOL lattice for integer values (i.e. not just 1/0)
  • Run physical system simulations based on applications of cellular automaton:
    • Computational fluid dynamics
    • Population dynamics
    • Ising Models
    • Other interesting cellular automaton: Rule 90, Langton's ant
    • Boolean binary logic rules (i.e. consider the 1 cell + 4 neighbours as a 5 bit input - 1 bit output to a logic circuit)
    • Discretise and extend to 2D my previous research in rho signalling in cell-cell junctions during collective cell migration

Usage

Current usage simply displays the simulation onto the terminal. Usage:

> Go-L --help
Usage of Go-L:
  -aliveratio float
    	The fraction of squares that start as alive, assigned at random. Domain: [0.0, 1.0]. (default 0.8)
  -gridsize uint
    	Length of square grid to define game on. (default 20)
  -iterations uint
    	Max number of iterations to simulate game of life. If stable solution, will exit early. (default 100)
  -topology string
    	Specify the topology of the grid (as a fundamental topology from a parallelograms). Valid parameters: BORDERED, TORUS, KLEIN_BOTTLE, PROJECTIVE_PLANE, SPHERE. (default "BORDERED")
  -updatedelay uint
    	Additional period delay between updating rounds of the game, in milliseconds. Does not take into account processing time. (default 200)
  -updaterule uint
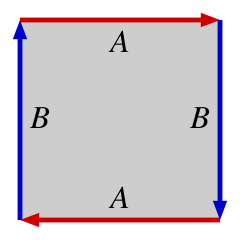
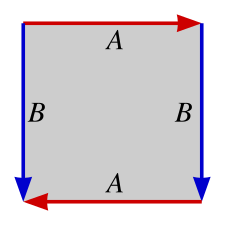
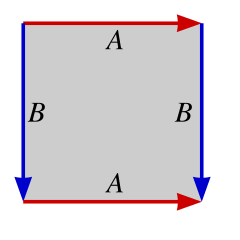
    	Specify the number associated with the update rule to use. Default to Conway's Game of Life. (default 1994975360)

Border Topologies

In redefining how the border conditions work, we can simulate GOL as if it was played on a variety of manifolds. This is most clearly seen when looking at the fundamental polygons derived from a square (or parallelogram). When considering the neighbours of a cell on the border of the lattice, a fundamental polygon helps show where the neighbouring values should be.

Sphere Real Projective Plane Klein Bottle Torus
Sphere Real Projective Plane Klein Bottle Torus

Consider a square lattice of size 5, coordinates indexed in $[0,4] \times [0,4]$. For a standard coordinate, say $(2,2)$, its neighbours are: ${(1,2),(3,2),(2,1),(2,3)}$. These are all within standard bounds. Now consider the point $(4,2)$ with neighbours: ${(3,2),(5,2),(4,1),(4,3)}$. What value should we use for $(5,2)$? The topology dictates how lattice-border neighbours get selected. For a bordered topology, there is nothing outside of lattice, therefore index it the null value (or 0 in GOL rules). For a sphere, the $(5,2)$ becomes $(2,0)$ given its equivalence relation (on an $n$ square lattice):

$$ \displaylines{ (x, 0) \backsim (n, n-x), \quad x\in [0, n] \\ (x, n) \backsim (0, n-x), \quad x\in [0, n] } $$

Or for a torus

$$ \displaylines{ (x, 0) \backsim (x, n), \quad x\in [0, n] \\ (0, y) \backsim (n, y), \quad y\in [0, n] } $$

or a real projective plane

$$ \displaylines{ (0, y) \backsim (n, n-y), \quad y\in [0, n] \\ (x, 0) \backsim (n-x, n), \quad x\in [0, n] } $$

and lastly a klein bottle

$$ \displaylines{ (0, y) \backsim (n, y), \quad y\in [0, n] \\ (x, 0) \backsim (n-x, n), \quad x\in [0, n] } $$

For update rules that consider 2nd degree neighbours (i.e. $(6,2)$ ), the mapping gets a bit more complicated.

More on Game of Life

A cellular automaton designed by mathematician John Conway showing how complex emergent behaviour can arise from simple rules. In his case, at each future timestamp, a cell will be updated, based on its four neighbouring cells:

  1. A live cell will survive if only 2 or 3 of its neighbours are alive
  2. A dead cell with 3 alive neighbours will become alive
  3. All other cells die.

Update Rules

Conway's Game of Life is but one 2D cellular automata that depends only on its 4 direct neighbours. One can conceive of other update rules. If one considers the five relevant cells: left, cell, right, up & down, there are then $2^5=32$ possible states to consider. An update rule can be defined as follows.

  1. Define an ordered set on the 32 possible states $ { s_i }_{i=0}^{32} $
  2. Create a 32 digit binary number, $B$, where $B_i = 1$ iff the update rule maps the cell with state $S_i$ to 1.
  3. All update rules can be then indexed from this, $U_B : {0,1}^5 \to { 0, 1}$

Update Rules: 1D example

Consider a simple 1D case of: left, cell, right. There are 8 states with a natural indexing: $111, 110, 101, 100, 011, 010, 001, 000$. An example update rule $U_{177}$ updates the cell to 1 in the following cases: 111, 101, 100, 000 (all other cases to 0). With the binary expansion $177 = 10110001b$, this can be expressed simply below:

111 110 101 100 011 010 001 000
1 0 1 1 0 0 0 1

2D Implementation

In this repo, we consider a similar binary representation for cells: left, cell, right, up, down and a natural indexing $11111, 11110, 11101, ..., 00001, 00000$. This creates $2^5=32$ possible states and therefore $2^{32} = 4294967296$ possible update rules (conveniently fitting in a 32-bit integer).

We can now consider the update rule in Conway's Game of Life:

  1. Alive and 3 neighbours: 01111, 10111, 11101, 11110 ([15, 23, 29, 30])
  2. Alive and 2 neighbours: 00111, 01101, 01110, 10101, 10110, 11100 ([7, 13, 14, 21, 22, 28])
  3. Dead and 3 neighbours: 01011, 10011, 11001, 11010 ([11, 19, 25, 26])

Which gives a binary number with 1's at positions: [7, 11, 13, 14, 15, 19, 21, 22, 23, 25, 26, 28, 29, 30] or in binary: 01110110111010001110100010000000 or in base 10: 1994975360