Kar Ng 2021
- 1 R PACKAGES
- 2 INTRODUCTION
- 3 DATA PREPARATION
- 4 DATA CLEANING
- 5 EXPLORATORY DATA ANALYSIS (EDA)
- 5 Model Building
- 6 Model for Production
- 7 Conclusion
- 8 LEGALITY
- 9 REFERENCE
# R Libraries
library(tidyverse)
library(skimr)
library(caret)
library(MASS)
library(kableExtra)
library(qqplotr)
library(glmnet)
library(car)
library(corrplot)
library(mgcv)
library(randomForest)
library(doParallel)
library(pls)
library(tidytext)
# R setting
options(scipen = 0)This project uses a public dataset named “Boston” from a R package - “MASS”. It is a famous dataset for machine learning practitioners. However, I have made some adjustments to this dataset to make overall analysis more interesting and unique.
This Boston dataset studies the effects of a range of variables on median house prices in Boston in late 70s, United States.
I will statistically analyse the dataset and make predictions with machine learning algorithms. Then, I will study the effects of each variables on the median house prices, pick a model that has the highest predictive power, and build an online interactive application by using RShiny in section 6 - Model for Production.
Highlights of some upcoming graphs
This section imports the edited version of the dataset. Following is 10 rows of data randomly selected from the dataset.
boston <- read.csv("boston.csv")
sample_n(boston, 10)## X crime.rate resid.zone indus.biz charles.river nitrogen.oxide room age
## 1 452 5.44114 0.0 18.10 0 0.713 6.655 98.2
## 2 127 0.38735 0.0 25.65 0 0.581 5.613 95.6
## 3 173 0.13914 0.0 4.05 0 0.510 5.572 88.5
## 4 311 2.63548 0.0 9.90 0 0.544 4.973 37.8
## 5 289 0.04590 52.5 5.32 0 0.405 6.315 45.6
## 6 79 0.05646 0.0 12.83 0 0.437 6.232 53.7
## 7 150 2.73397 0.0 19.58 0 0.871 5.597 94.9
## 8 208 0.25199 0.0 10.59 0 0.489 5.783 72.7
## 9 167 2.01019 0.0 19.58 0 0.605 7.929 96.2
## 10 72 0.15876 0.0 10.81 0 0.413 5.961 17.5
## dist.to.work highway.index property.tax pt.ratio black lstat house.value
## 1 2.3552 24 666 20.2 355.29 NA 15.2
## 2 1.7572 2 188 19.1 359.29 27.26 15.7
## 3 2.5961 5 296 16.6 396.90 14.69 23.1
## 4 2.5194 4 304 18.4 350.45 12.64 16.1
## 5 7.3172 6 293 16.6 396.90 7.60 22.3
## 6 5.0141 5 398 18.7 386.40 12.34 21.2
## 7 1.5257 5 403 14.7 351.85 21.45 15.4
## 8 4.3549 4 277 18.6 389.43 18.06 22.5
## 9 2.0459 5 403 14.7 369.30 3.70 50.0
## 10 5.2873 4 305 19.2 376.94 9.88 21.7
The dataset has important information regarding factors that may affect the price of a house in Boston in late 70s. For examples, crime rate, number of rooms in the house, nitrogen oxides concentration, its proximity to industrial area, employment centers, highways and etc.
The unit of the house value is “median house price”. Believing this median values is extracted from multiple houses in the respective regions in the city.
Following is the data description adapted from the relevant R package.
Variables <- names(boston[2:15])
Description <- c("Per capita crime rate by town.",
"Proportion of residential land zoned for lots over 25,000 sq.ft.",
"Proportion of non-retail business acres per town.",
"Charles River dummy variable (= 1 if tract bounds river; 0 otherwise).",
"Nitrogen oxides concentration (parts per 10 million).",
"Average number of rooms per dwelling.",
"Proportion of owner-occupied units built prior to 1940.",
"Weighted mean of distances to five Boston employment centres.",
"Index of accessibility to radial highways.",
"Full-value property-tax rate per per $10,000.",
"Pupil-teacher ratio by town.",
"1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town.",
"lower status of the population (percent).",
"Median value of owner-occupied homes in per $1000s.")
data.frame(Variables, Description) %>%
kbl() %>%
kable_styling(bootstrap_options = c("hover", "bordered", "stripped"))| Variables | Description |
|---|---|
| crime.rate | Per capita crime rate by town. |
| resid.zone | Proportion of residential land zoned for lots over 25,000 sq.ft. |
| indus.biz | Proportion of non-retail business acres per town. |
| charles.river | Charles River dummy variable (= 1 if tract bounds river; 0 otherwise). |
| nitrogen.oxide | Nitrogen oxides concentration (parts per 10 million). |
| room | Average number of rooms per dwelling. |
| age | Proportion of owner-occupied units built prior to 1940. |
| dist.to.work | Weighted mean of distances to five Boston employment centres. |
| highway.index | Index of accessibility to radial highways. |
| property.tax | Full-value property-tax rate per per $10,000. |
| pt.ratio | Pupil-teacher ratio by town. |
| black | 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town. |
| lstat | lower status of the population (percent). |
| house.value | Median value of owner-occupied homes in per $1000s. |
The dataset has 506 rows of observations and 14 columns of variables. All variables are in numerical form.
glimpse(boston) ## Rows: 506
## Columns: 15
## $ X <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, ~
## $ crime.rate <dbl> 0.00632, 0.02731, 0.02729, 0.03237, 0.06905, 0.02985, 0~
## $ resid.zone <dbl> 18.0, 0.0, 0.0, 0.0, 0.0, 0.0, 12.5, 12.5, 12.5, 12.5, ~
## $ indus.biz <dbl> 2.31, 7.07, 7.07, 2.18, 2.18, 2.18, 7.87, 7.87, 7.87, 7~
## $ charles.river <int> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
## $ nitrogen.oxide <dbl> 0.538, 0.469, 0.469, 0.458, 0.458, 0.458, 0.524, 0.524,~
## $ room <dbl> 6.575, 6.421, 7.185, 6.998, 7.147, 6.430, 6.012, 6.172,~
## $ age <dbl> 65.2, 78.9, 61.1, 45.8, 54.2, 58.7, 66.6, 96.1, 100.0, ~
## $ dist.to.work <dbl> 4.0900, 4.9671, 4.9671, 6.0622, 6.0622, 6.0622, 5.5605,~
## $ highway.index <int> 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4~
## $ property.tax <int> 296, 242, 242, 222, 222, 222, 311, 311, 311, 311, 311, ~
## $ pt.ratio <dbl> 15.3, 17.8, 17.8, 18.7, 18.7, 18.7, 15.2, 15.2, 15.2, 1~
## $ black <dbl> 396.90, 396.90, 392.83, 394.63, 396.90, NA, 395.60, 396~
## $ lstat <dbl> 4.98, 9.14, 4.03, 2.94, 5.33, 5.21, 12.43, 19.15, 29.93~
## $ house.value <dbl> 24.0, 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 1~
From observation, “charles.river” is either 0 or 1, and therefore it should be a categorical variable and it should be assigned with factor type. The first variable, “x”, has to be removed because it is just row number and irrelevant.
There are 12 and 17 missing data in the “black” and “lstat” column. Fortunately, the completeness of these two variables are 97.6% and 96.6%. It is a matter of choice whether one wants to remove these values or apply imputation techniques. I will go with the later as it is my purpose to induce these missing values using imputation model using R.
skim_without_charts(boston)| Name | boston |
| Number of rows | 506 |
| Number of columns | 15 |
| \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ | |
| Column type frequency: | |
| numeric | 15 |
| \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ | |
| Group variables | None |
Variable type: numeric
| skim\_variable | n\_missing | complete\_rate | mean | sd | p0 | p25 | p50 | p75 | p100 |
|---|---|---|---|---|---|---|---|---|---|
| X | 0 | 1.00 | 253.50 | 146.21 | 1.00 | 127.25 | 253.50 | 379.75 | 506.00 |
| crime.rate | 0 | 1.00 | 3.61 | 8.60 | 0.01 | 0.08 | 0.26 | 3.68 | 88.98 |
| resid.zone | 0 | 1.00 | 11.36 | 23.32 | 0.00 | 0.00 | 0.00 | 12.50 | 100.00 |
| indus.biz | 0 | 1.00 | 11.14 | 6.86 | 0.46 | 5.19 | 9.69 | 18.10 | 27.74 |
| charles.river | 0 | 1.00 | 0.07 | 0.25 | 0.00 | 0.00 | 0.00 | 0.00 | 1.00 |
| nitrogen.oxide | 0 | 1.00 | 0.55 | 0.12 | 0.38 | 0.45 | 0.54 | 0.62 | 0.87 |
| room | 0 | 1.00 | 6.28 | 0.70 | 3.56 | 5.89 | 6.21 | 6.62 | 8.78 |
| age | 0 | 1.00 | 68.57 | 28.15 | 2.90 | 45.02 | 77.50 | 94.07 | 100.00 |
| dist.to.work | 0 | 1.00 | 3.80 | 2.11 | 1.13 | 2.10 | 3.21 | 5.19 | 12.13 |
| highway.index | 0 | 1.00 | 9.55 | 8.71 | 1.00 | 4.00 | 5.00 | 24.00 | 24.00 |
| property.tax | 0 | 1.00 | 408.24 | 168.54 | 187.00 | 279.00 | 330.00 | 666.00 | 711.00 |
| pt.ratio | 0 | 1.00 | 18.46 | 2.16 | 12.60 | 17.40 | 19.05 | 20.20 | 22.00 |
| black | 12 | 0.98 | 355.85 | 92.24 | 0.32 | 374.71 | 391.38 | 396.12 | 396.90 |
| lstat | 17 | 0.97 | 12.59 | 7.16 | 1.73 | 6.86 | 11.32 | 16.94 | 37.97 |
| house.value | 0 | 1.00 | 22.53 | 9.20 | 5.00 | 17.02 | 21.20 | 25.00 | 50.00 |
Alternatively, I can examine missing data in the dataset by following code. There are 12 missing data in the column “black”, and 17 from the column “lstat”.
colSums(is.na(boston))## X crime.rate resid.zone indus.biz charles.river
## 0 0 0 0 0
## nitrogen.oxide room age dist.to.work highway.index
## 0 0 0 0 0
## property.tax pt.ratio black lstat house.value
## 0 0 12 17 0
Following is a summary summarises some basic descriptive statistics of the dataset.
summary(boston)## X crime.rate resid.zone indus.biz
## Min. : 1.0 Min. : 0.00632 Min. : 0.00 Min. : 0.46
## 1st Qu.:127.2 1st Qu.: 0.08205 1st Qu.: 0.00 1st Qu.: 5.19
## Median :253.5 Median : 0.25651 Median : 0.00 Median : 9.69
## Mean :253.5 Mean : 3.61352 Mean : 11.36 Mean :11.14
## 3rd Qu.:379.8 3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10
## Max. :506.0 Max. :88.97620 Max. :100.00 Max. :27.74
##
## charles.river nitrogen.oxide room age
## Min. :0.00000 Min. :0.3850 Min. :3.561 Min. : 2.90
## 1st Qu.:0.00000 1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02
## Median :0.00000 Median :0.5380 Median :6.208 Median : 77.50
## Mean :0.06917 Mean :0.5547 Mean :6.285 Mean : 68.57
## 3rd Qu.:0.00000 3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08
## Max. :1.00000 Max. :0.8710 Max. :8.780 Max. :100.00
##
## dist.to.work highway.index property.tax pt.ratio
## Min. : 1.130 Min. : 1.000 Min. :187.0 Min. :12.60
## 1st Qu.: 2.100 1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40
## Median : 3.207 Median : 5.000 Median :330.0 Median :19.05
## Mean : 3.795 Mean : 9.549 Mean :408.2 Mean :18.46
## 3rd Qu.: 5.188 3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20
## Max. :12.127 Max. :24.000 Max. :711.0 Max. :22.00
##
## black lstat house.value
## Min. : 0.32 Min. : 1.73 Min. : 5.00
## 1st Qu.:374.71 1st Qu.: 6.86 1st Qu.:17.02
## Median :391.38 Median :11.32 Median :21.20
## Mean :355.85 Mean :12.59 Mean :22.53
## 3rd Qu.:396.12 3rd Qu.:16.94 3rd Qu.:25.00
## Max. :396.90 Max. :37.97 Max. :50.00
## NA's :12 NA's :17
Insights
-
I can see that there are missing values in the “black” and “lstat” as represented by “NA”.
-
The feature “charles.river” is a binary type with either 0 or 1.
This part converts the dataset into a format that is appropriate for analysis or storage.
Depending on context, my usual cleaning techniques include but not limited to the following:
- Renaming of columns and levels if required.
- Long-wide structure transformation if required.
- Replacing NA by any appropriate imputation means.
- Removing variables that do not contribute or irrelevant to the prediction of the responding variable.
- Removing variables that have too many missing values (generally said a 60% missing values).
- Removing rows that have many missing values.
- Factorise variables (or known as features).
- Feature engineering if required.
Several specific cleaning tasks identified from the previous section:
- Remove the first column “x”.
- Convert “charles.river” from integer into factor.
- Imputation and create new associated features.
Following code remove first column “X” which is the row number, and factorise the binary column, “charles.river” to convert it into factor.
boston <- boston %>%
dplyr::select(-1) %>%
mutate(charles.river = as.factor(charles.river))I am applying caret function for this imputation. I will first convert the factor variable “charles river” in the dataset into dummy data as it is required by the package caret imputation to work.
# Dummy transformation of factorised Charles river because caret function only work with dummy data.
dummy.variable <- dummyVars(~., data = boston[, -14])
boston.dummy <- dummy.variable %>% predict(boston[, -14])Assessing again the number of missing values in this transformed dataset.
colSums(is.na(boston.dummy)) ## crime.rate resid.zone indus.biz charles.river.0 charles.river.1
## 0 0 0 0 0
## nitrogen.oxide room age dist.to.work highway.index
## 0 0 0 0 0
## property.tax pt.ratio black lstat
## 0 0 12 17
Now, I am building an imputation model that uses all columns in the dataset to predict these missing values, by the method of “Bagged Decision Trees”.
# Imputation
imputation.model <- preProcess(boston.dummy, method = "bagImpute")
imputed.boston <- imputation.model %>% predict(boston.dummy)And the missing values have now been filled up by imputation.
colSums(is.na(imputed.boston))## crime.rate resid.zone indus.biz charles.river.0 charles.river.1
## 0 0 0 0 0
## nitrogen.oxide room age dist.to.work highway.index
## 0 0 0 0 0
## property.tax pt.ratio black lstat
## 0 0 0 0
Over-writing the original “black” and “lstat” with the newly imputed “black” and “lstat” columns.
boston$black <- imputed.boston[, 13]
boston$lstat <- imputed.boston[, 14]Now, there are no more missing values in the dataset.
colSums(is.na(boston))## crime.rate resid.zone indus.biz charles.river nitrogen.oxide
## 0 0 0 0 0
## room age dist.to.work highway.index property.tax
## 0 0 0 0 0
## pt.ratio black lstat house.value
## 0 0 0 0
Since the purpose of this project is to assess the effects of each of these variables in predicting the median house prices. I will keep all variables at this point. I will make variable selection again in later analysis.
Let’s have a final glimpse of the data again.
# Convert 2 integers variable "highway.index" and "property.tax " to double type.
boston <- boston %>%
mutate_if(is.integer, as.double)
glimpse(boston)## Rows: 506
## Columns: 14
## $ crime.rate <dbl> 0.00632, 0.02731, 0.02729, 0.03237, 0.06905, 0.02985, 0~
## $ resid.zone <dbl> 18.0, 0.0, 0.0, 0.0, 0.0, 0.0, 12.5, 12.5, 12.5, 12.5, ~
## $ indus.biz <dbl> 2.31, 7.07, 7.07, 2.18, 2.18, 2.18, 7.87, 7.87, 7.87, 7~
## $ charles.river <fct> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0~
## $ nitrogen.oxide <dbl> 0.538, 0.469, 0.469, 0.458, 0.458, 0.458, 0.524, 0.524,~
## $ room <dbl> 6.575, 6.421, 7.185, 6.998, 7.147, 6.430, 6.012, 6.172,~
## $ age <dbl> 65.2, 78.9, 61.1, 45.8, 54.2, 58.7, 66.6, 96.1, 100.0, ~
## $ dist.to.work <dbl> 4.0900, 4.9671, 4.9671, 6.0622, 6.0622, 6.0622, 5.5605,~
## $ highway.index <dbl> 1, 2, 2, 3, 3, 3, 5, 5, 5, 5, 5, 5, 5, 4, 4, 4, 4, 4, 4~
## $ property.tax <dbl> 296, 242, 242, 222, 222, 222, 311, 311, 311, 311, 311, ~
## $ pt.ratio <dbl> 15.3, 17.8, 17.8, 18.7, 18.7, 18.7, 15.2, 15.2, 15.2, 1~
## $ black <dbl> 396.9000, 396.9000, 392.8300, 394.6300, 396.9000, 386.9~
## $ lstat <dbl> 4.98000, 9.14000, 4.03000, 2.94000, 5.33000, 5.21000, 1~
## $ house.value <dbl> 24.0, 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 1~
Perfection.
Transforming the data frame for effective EDA.
bos <- boston %>%
gather(key = "key", value = "value") %>%
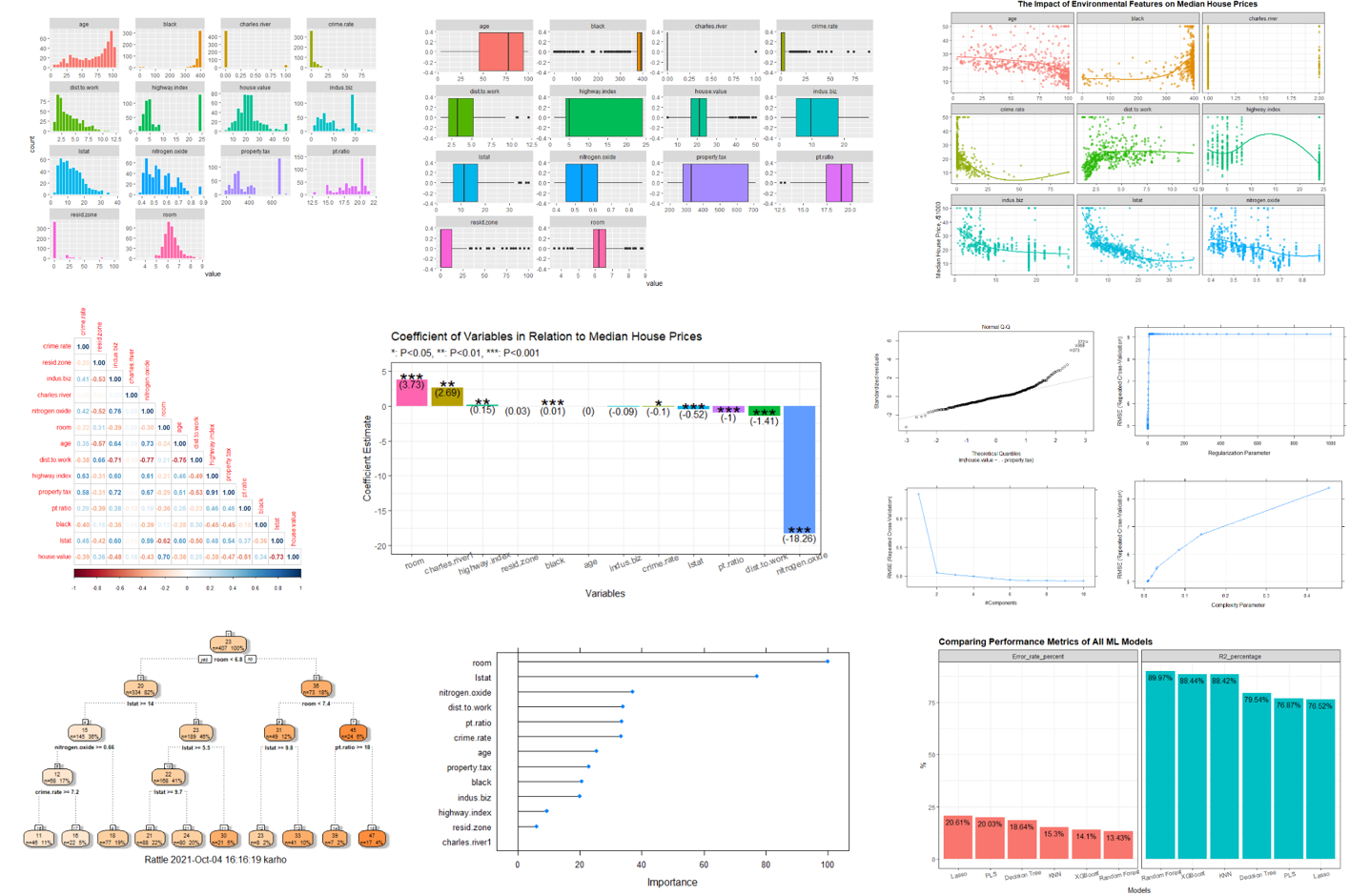
mutate(value = as.numeric(value))This section studies data distribution of each variables. In general, any non-skewed distribution that closes to a Gaussian distribution would be more useful for the prediction of the house value. They would have good relation with the responding variable - “house.value”.
ggplot(bos, aes(x = value, fill = key)) +
geom_histogram(colour = "white", bins = 20) +
facet_wrap(~ key, scale = "free") +
theme(legend.position = "none")Insight:
- The charles.river has a binary distribution with value in either 1 or 0.
- The room has a distribution that closes to Gaussian distribution.
- The y variable house.value has a nearly Gaussian distributed distribution which is a good sign.
- Many variables except charles.river and room seems to have skewed to both directions.
This part would help in manual selection of features when trying to make the prediction based on traditional linear regression that sensitive to outliers. Outliers are probably the reasons causing these skews. However, choosing a type of machine learning model that robust to outliers, such as decision tree, will be an alternative powerful option.
This section uses boxplot as an alternative visualization of outliers.
ggplot(bos, aes(x = value, fill = key)) +
geom_boxplot() +
facet_wrap(~ key, scale = "free") +
theme(legend.position = "none")Outliers exists in many variables include black, crime.rate, dist.to.work, lstat, house.value, ptratio, resid.zone, and even in the Gaussian distributed room。
The distribution plots and box plots show that the assumptions of linear regression have been violated and therefore a non-linear regression would perform better than linear regression algorithm, such as KNN and tree-base algorithms.
In relation to median house prices, visualisation shows that:
bos2 <- boston %>%
mutate(charles.river = as.numeric(charles.river)) %>%
pivot_longer(c(1:13), names_to = "variable", values_to = "result") %>%
arrange(variable)
# plot
ggplot(bos2, aes(x = result, y = house.value, colour = variable)) +
geom_point(alpha = 0.5) +
facet_wrap(~variable, scales = "free_x", ncol = 3) +
theme_bw() +
theme(legend.position = "none",
plot.title = element_text(face = "bold", size = 14, hjust = 0.5, vjust = 2),
strip.text = element_text(size = 10)) +
geom_smooth(se = F) +
labs(x = "Variables",
y = "Median House Price, /$1000",
title = "The Impact of Environmental Features on Median House Prices")Insights:
-
The variables that related (either positive or negative) the most with the median house prices are “room”, “lstat”, “pt.ratio”, and probably “resid.zone”.
-
The relationships of other variables with the median house price are not as much.
-
The relationships between the median house prices and each of the independent variables are not linear.
This section tests for the existence of multicollinearity within the dataset. It is a problem when two or more predictor variables are correlated with each other. One of the assumption of linear regression is to have predictor variables independent from each other. Multicollinearity can violate this assumption.
The existence of multicollinearity will increase the standard errors of coefficients estimates in the linear regression model, eventually alter the 95% Confidence intervals and finally affect the accuracy of P-values of each variables in relation to the median house prices. These P-values are the statistical metrics that we use to evaluate the significance of relationships between predictors with the median house prices.
A correlogram is graphed to study the interaction between each pair of the independent variables.
boston_cor <- boston %>%
mutate(charles.river = as.numeric(charles.river)) %>%
cor()
corrplot::corrplot(boston_cor, method = "number", type = "lower")Generally speaking, an absolute correlation value that is around and higher than 50% indicates a moderate correlation. The closer to 1 in either positive or negative direction, the higher the relationship between the two variables. As a rule thumb, multicollinearity problem is an issue when the correlation between the two independent variables exceed 0.8 or -0.8.
Therefore, multicollinearity issue is likely to happen between “highway index” and “property tax”. They have a correlation degree of 0.91. To avoid multicollinearity problem, one should avoid the coexistence of the two variables in a model. This can be achieved by manual selection or auto-selection by machine learning algorithms. Alternatively, a machine learning algorithm that immune to multicollinearity should be selected during model building.
An alternative, popular multicollinearity detection method, called variance inflation factor (VIF) will be performed in next section. This method requires a model to be built prior to evaluation. VIF will further confirm the result of multicollinearity detection by this correlogram.
This section creates data partitions into 80% of train set and 20% test set. The train set will be used to build models and the test set will be used to evaluate the performance of each models.
set.seed(123)
# Create data partition
train.index <- boston$house.value %>% createDataPartition(p = 0.8, list = F)
# Get train and test set
train.data <- boston[train.index, ]
test.data <- boston[-train.index, ]A multiple linear regression is created to study the effect of each variables on the median house prices.
# Using original dataset to include all data into this model
model_mlr <- lm(house.value ~., data = train.data)As mentioned, a variance inflation factor (VIF) evaluation is performed. A VIF that exceeds 5 indicates a problematic amount of collinearity (James et al. 2014). The result matches the outcome from the previous correlogram that “highway.index” and “property.tax” correlated and should not be coexist in a linear regression model to avoid the issue of multicollinearity.
vif(model_mlr)## crime.rate resid.zone indus.biz charles.river nitrogen.oxide
## 1.850426 2.322953 3.954415 1.066675 4.447359
## room age dist.to.work highway.index property.tax
## 1.967852 3.218367 4.062105 8.151202 9.660457
## pt.ratio black lstat
## 1.850979 1.358039 3.183534
Following are two linear models built with the exception of either highway.index or property.tax. Their adjusted R-Squared will be compared and the model with the higher adjusted R-squared will be selected.
set.seed(123)
model2 <- lm(house.value ~. - highway.index , data = train.data)
summary(model2)##
## Call:
## lm(formula = house.value ~ . - highway.index, data = train.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.111 -2.647 -0.544 1.532 30.661
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3.005e+01 5.662e+00 5.308 1.86e-07 ***
## crime.rate -5.673e-02 3.956e-02 -1.434 0.15234
## resid.zone 3.190e-02 1.661e-02 1.921 0.05549 .
## indus.biz -8.867e-02 7.062e-02 -1.256 0.21004
## charles.river1 2.788e+00 9.759e-01 2.857 0.00451 **
## nitrogen.oxide -1.505e+01 4.495e+00 -3.349 0.00089 ***
## room 3.931e+00 4.733e-01 8.306 1.61e-15 ***
## age -8.337e-04 1.616e-02 -0.052 0.95889
## dist.to.work -1.433e+00 2.407e-01 -5.954 5.78e-09 ***
## property.tax 2.306e-03 2.735e-03 0.843 0.39963
## pt.ratio -8.590e-01 1.544e-01 -5.563 4.92e-08 ***
## black 1.003e-02 3.051e-03 3.288 0.00110 **
## lstat -5.065e-01 6.292e-02 -8.050 9.87e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 5.012 on 394 degrees of freedom
## Multiple R-squared: 0.71, Adjusted R-squared: 0.7011
## F-statistic: 80.37 on 12 and 394 DF, p-value: < 2.2e-16
set.seed(123)
model3 <- lm(house.value ~. - property.tax , data = train.data)
summary(model3)##
## Call:
## lm(formula = house.value ~ . - property.tax, data = train.data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.3928 -2.9648 -0.4773 1.6840 29.7623
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 34.865352 5.790622 6.021 3.97e-09 ***
## crime.rate -0.097869 0.040475 -2.418 0.016060 *
## resid.zone 0.028180 0.016060 1.755 0.080094 .
## indus.biz -0.094363 0.066490 -1.419 0.156630
## charles.river1 2.707097 0.961757 2.815 0.005127 **
## nitrogen.oxide -18.526772 4.464029 -4.150 4.07e-05 ***
## room 3.750065 0.471435 7.955 1.93e-14 ***
## age 0.002493 0.016013 0.156 0.876347
## dist.to.work -1.420026 0.237928 -5.968 5.35e-09 ***
## highway.index 0.151057 0.048030 3.145 0.001787 **
## pt.ratio -1.002199 0.154700 -6.478 2.77e-10 ***
## black 0.011176 0.003022 3.698 0.000248 ***
## lstat -0.510478 0.062202 -8.207 3.27e-15 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.955 on 394 degrees of freedom
## Multiple R-squared: 0.7165, Adjusted R-squared: 0.7079
## F-statistic: 83 on 12 and 394 DF, p-value: < 2.2e-16
The model without property.tax (model 3) has higher adjusted R-squared at 0.708 as compared to 0.7012 of the previous model without highway.index. Additionally, the RSE of this model (model 3) is 4.954 which is lower than the previous model (model 2) built with property tax at 5.012. Therefore, property.tax should be dropped to avoid multicollinearity.
Model performance
-
P-value of the F-Statistics of this model is < 0.05, indicating that there is at least of the predictor variable is significantly related to the median house prices.
-
The adjusted R-squared of this model is 0.7091, which is a good value indicating that this multiple linear regression model is able to explain 70.91% of the variation in the median house prices.
-
The Residual standard error (RSE) is 4.954, This corresponds to an error rate of 22%, which is acceptable but high enough to investigate a better model for prediction.
4.954/mean(Boston$medv)## [1] 0.2198572
Insights from coefficient estimates
Following visualisation indicates the strength of coefficients and significance level of each variable in relation to the median house price.
# set up df
coef_plot <- data.frame(summary(model3)$coef) %>%
rownames_to_column(var = "variable") %>%
filter(variable != "(Intercept)") %>%
rename(P_value = "Pr...t..") %>%
mutate(sig = case_when(P_value < 0.05 & P_value > 0.01 ~ "*",
P_value < 0.01 & P_value > 0.001 ~ "**",
P_value < 0.001 ~ "***",
TRUE ~ " "))
# plot
plot_mlr <- ggplot(coef_plot, aes(y = Estimate, x = fct_reorder(variable, -Estimate), fill = variable)) +
geom_bar(stat = "identity") +
theme_bw() +
theme(legend.position = "none",
axis.text.x = element_text(angle = 20, size = 10, hjust = 0.7),
plot.margin = unit(c(1,1,1,1), "cm")) +
geom_text(aes(label = paste0("(", round(Estimate, 2), ")")), vjust = 1) +
geom_text(aes(label = sig), size = 8) +
labs(x = "Variables",
y = "Coefficient Estimate",
subtitle = "*: P<0.05, **: P<0.01, ***: P<0.001",
title = "Coefficient of Variables in Relation to Median House Prices")+
scale_y_continuous(lim = c(-20, 5), breaks = seq(-20, 5, 5))
plot_mlr-
Variables “resid.zone”, “age”, and “indus.biz” do not have significant relationship with the median house prices.
-
Variable “room” has the highest significant positive impact on median house prices.
-
Variable “nitrogen oxide” has the highest significant negative impact on median house prices.
This section describes whether the assumptions of linear regression is fulfilled.
- The relationship between independent variables and the responding variable is non-linear.
plot(model3, 1)-
The second assumption is that independent variables should be independent from each other. It is not the case in this dataset as there is multicollinearity problem between “rad” and “tax”.
-
Following plot the standardised residual against the fitted values shows that the amount of error is not similar at each data point of the linear model and therefore it has a feature of heteroscedasticity.
plot(model3, 3) * There is
also no multivariate normality shown by a standard Q-Q plot below formed
by the multiple linear regression model. An ideal trend would be having
all points falling near the straight line in the middle of the plot and
form a line.
* There is
also no multivariate normality shown by a standard Q-Q plot below formed
by the multiple linear regression model. An ideal trend would be having
all points falling near the straight line in the middle of the plot and
form a line.
plot(model3, 2)This dataset has a non-parametric characteristics and therefore a non-parameter machine learning prediction model should be selected.
This section I will still apply a parametric algorithm, Lasso regression, to check out how would the L1-norm lambda regularisation of this method performs. The performance metrics of this method will be used as a baseline model to compared with non-parametric machine learning algorithms that I am going to apply later.
set.seed(123)
# build the model
model_lasso <- train(house.value ~., data = boston,
method = "glmnet",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
tuneGrid = expand.grid(alpha = 1,
lambda = 10^seq(-3, 3, length = 100)))From above lasso model, I built a grid that contains many lambda value, and it seems like the best one will be closing to 0. A best lambda value is the one that having the lowest RMSE.
plot(model_lasso)R caret package automatically identified the best lambda for me which is 0.0284.
model_lasso$bestTune## alpha lambda
## 25 1 0.02848036
Interesting, many materials state that Lasso regression should be used when there is multicollinearity issue in the dataset because Lasso will select 1 variable from the highly correlated group. However, it is not happening in my case. The “highway.index” and “property.tax” are correlated with a VIF above 5 and therefore they should not coexist in a model as it would affect the accuracy of the coefficients.
coef(model_lasso$finalModel, model_lasso$bestTune$lambda)## 14 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) 33.356306822
## crime.rate -0.098037818
## resid.zone 0.040977343
## indus.biz .
## charles.river1 2.728770377
## nitrogen.oxide -16.819538218
## room 3.983906294
## age -0.001178914
## dist.to.work -1.393107610
## highway.index 0.249337291
## property.tax -0.009863429
## pt.ratio -0.938732462
## black 0.010230970
## lstat -0.486118949
It is likely that a the best lambda is determined based on the lowest point of RMSE. Therefore, I initiate a trade-off here. I manually selected the lambda value that will exclude either one from the high correlated group.
# build the model
model_lasso <- train(house.value ~., data = boston,
method = "glmnet",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
tuneGrid = expand.grid(alpha = 1,
lambda = 0.19)) # I manually found that lambda 0.19 have property.tax removed that is highly correlated with highway.index
coef(model_lasso$finalModel, model_lasso$bestTune$lambda)## 14 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) 22.705984523
## crime.rate -0.042736919
## resid.zone 0.017057697
## indus.biz -0.011979494
## charles.river1 2.506987924
## nitrogen.oxide -10.274618753
## room 4.312002138
## age .
## dist.to.work -0.853110646
## highway.index 0.004299630
## property.tax .
## pt.ratio -0.835671318
## black 0.008703587
## lstat -0.485833341
Following compute the R2 and RMSE of Lasso from predicting the test data. It will be recorded in the last section for a grand model comparison.
# predictions
prediction_lasso <- model_lasso %>% predict(test.data)
# model performance
R2_lasso <- caret::R2(prediction_lasso, test.data$house.value)
RMSE_lasso <- RMSE(prediction_lasso, test.data$house.value)
R2_lasso## [1] 0.7658617
RMSE_lasso## [1] 4.658006
A principle component technique is applied in this section, called Partial Least Squares (PLS). PLS is a method that can avoid multicollinearity between PLS summarises the predictors into a few new variables called principle component. Then, these new variables are fit to linear regression model.
set.seed(123)
model_pls <- train(house.value ~., data = train.data,
method = "pls",
scale = TRUE,
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
tuneLength = 10)This is a plot showing how are the numbers of principal components (PCs) in relation to RMSE. The lower the RMSE, the lower the model. The optimum level of PC should be around 8 to 10.
plot(model_pls)R can help to identify the best number of components (ncomp) to be used in the model, which is 9. This value will be automatically set as the default “ncomp” to be used during prediction.
model_pls$bestTune## ncomp
## 9 9
Internally, this model captures 90.89% of variation in the 9 components and 72.21% of the outcome variation.
summary(model_pls$finalModel)## Data: X dimension: 407 13
## Y dimension: 407 1
## Fit method: oscorespls
## Number of components considered: 9
## TRAINING: % variance explained
## 1 comps 2 comps 3 comps 4 comps 5 comps 6 comps 7 comps
## X 46.89 57.25 64.46 69.91 75.73 79.83 83.17
## .outcome 48.82 69.04 70.50 71.49 71.89 72.03 72.12
## 8 comps 9 comps
## X 85.80 90.89
## .outcome 72.19 72.19
In predicting the test variable, PLS has done a little better job than lasso in terms of R2 and RMSE. These metrics will be recorded for final grand comparison.
# Predictions
predictions_pls <- model_pls %>% predict(test.data)
# Model performance
caret::R2(predictions_pls, test.data$house.value)## [1] 0.7691915
caret::RMSE(predictions_pls, test.data$house.value)## [1] 4.527916
K-Nearest Neighbors (KNN) is the very first non-parametric model to be implemented. It does not need to comply with parametric assumptions as well as the collinearity issue. This method uses the neighboring points to make estimations during prediction.
model_knn <- train(house.value ~., data = boston,
method = "knn",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
preProcess = c("center", "scale"),
tuneLength = 10
)Grabbing the nearest 5 neighboring points during internal estimation and prediction had the lowest RMSE. Therefore, it is the optimum “k” nearest point that this model will be using during prediction on the test dataset.
plot(model_knn)model_knn$bestTune## k
## 1 5
Great, the result has an significant improvement from the parameter options.
# Predictions
predictions_knn <- model_knn %>% predict(test.data)
# Model performance
caret::R2(predictions_knn, test.data$house.value)## [1] 0.8846717
caret::RMSE(predictions_knn, test.data$house.value)## [1] 3.458302
Decision tree, also known as CART (Classification and Regression Tree) is my second non-parametric machine learning algorithm that work should very well in condition when there is highly non-linear relationship between the predictors and the responding variable. Decision tree has a upside-down tree-like structure with decision rules in each of the branch to guide the prediction of new observations.
I am expecting a better result because decision tree tend to prefer a situation that a few of variables in the variables list are more powerful than the others. This house dataset has this characteristic. Few of the powerful features are nitrogen.oxide, room, and charles.river. This method is also immune to multicollinearity.
set.seed(123)
model_DT <- train(house.value ~., data = train.data,
method = "rpart",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
tuneLength = 10) # Specifying the number of possible cp values for pruning, default is 3. Complexity parameter (CP) is the index set to prune the tree to avoid overfitting. The best CP detected is 0.0086 with the lowest RMSE.
plot(model_DT)model_DT$bestTune## cp
## 1 0.008601926
Following decision tree can help to visualise the important decisions to be made during each split.
par(xpd = NA)
plot(model_DT$finalModel, uniform = T, branch = 0.5, compress = T)
text(model_DT$finalModel, col = "darkgreen", fancy = F)Decision tree specifies the variable “room” as the root node (the node at the very top) after trying out all variables. On the root node, it appears that “room” leads to the purest two branches compared to other variables. Formally, It means that the information gain for the variable “room” is the highest. From the root node, we will know more about median house prices after looking at “room” compared to other variables. In regression decision tree, the value of each split cutoff point (for example “room < 6.838”) is selected to result the purest branch, or defined that residual sum of squared error (RSS) is minimized.
This computation is iterated at each resulting branches on sub-samples resulting from individual parent nodes until either maximum depth of the tree or when pure branches are achieved. This process is known as recursive partitioning.
To improve the visual, following is an alternative visual showing the exact same information as above tree however it shows the number of samples and associated proportion during each split.
library(rattle)## Loading required package: bitops
##
## Attaching package: 'bitops'
## The following object is masked from 'package:Matrix':
##
## %&%
## Rattle: A free graphical interface for data science with R.
## Version 5.4.0 Copyright (c) 2006-2020 Togaware Pty Ltd.
## Type 'rattle()' to shake, rattle, and roll your data.
##
## Attaching package: 'rattle'
## The following object is masked from 'package:randomForest':
##
## importance
fancyRpartPlot(model_DT$finalModel, palettes = "Oranges")Following is the decision rules defined in the model.
model_DT$finalModel## n= 407
##
## node), split, n, deviance, yval
## * denotes terminal node
##
## 1) root 407 34125.5800 22.51057
## 2) room< 6.8375 334 12681.2200 19.62695
## 4) lstat>=14.4 145 3819.0870 15.30483
## 8) nitrogen.oxide>=0.657 68 876.7047 12.45882
## 16) crime.rate>=7.16463 46 350.9915 10.85870 *
## 17) crime.rate< 7.16463 22 161.6695 15.80455 *
## 9) nitrogen.oxide< 0.657 77 1905.1950 17.81818 *
## 5) lstat< 14.4 189 4075.3230 22.94286
## 10) lstat>=5.51 168 2309.9490 22.09702
## 20) lstat>=9.705 88 616.5777 20.71591 *
## 21) lstat< 9.705 80 1340.8690 23.61625 *
## 11) lstat< 5.51 21 683.6381 29.70952 *
## 3) room>=6.8375 73 5959.9890 35.70411
## 6) room< 7.443 49 2037.2070 31.28367
## 12) lstat>=9.76 8 440.5750 23.02500 *
## 13) lstat< 9.76 41 944.5190 32.89512 *
## 7) room>=7.443 24 1010.4700 44.72917
## 14) pt.ratio>=17.6 7 465.9686 38.88571 *
## 15) pt.ratio< 17.6 17 207.0588 47.13529 *
# predictions
prediction_DT <- model_DT %>% predict(test.data)
# Model performance
caret::R2(prediction_DT, test.data$house.value)## [1] 0.7958708
caret::RMSE(prediction_DT, test.data$house.value)## [1] 4.211489
Decision tree is a powerful machine learning algorithm. However, it do come with its disadvantages. It is because that only one tree is built and therefore its result is highly relied on the training set that used in the split of the decision tree. Therefore, there might be significant impact on the tree if there is a small change in the dataset. The lower result above (79.58%) might be because that the decision tree was not generalise well and overfit the training data.
To solve this problem, next section I will build and aggregate many trees for do a better prediction, it is known as random forest. I will hope to see a boost in prediction accuracy on the test dataset.
Random forest, is also known as an ensemble learning or method because it aggregates many of decision trees, averaging the internally built models, and creating a final high-performance predictive model compared to decision tree.
This section will grow a high “data-diversity” random forest like many other projects in the world that used Random forest. All trees will not be completely the same. It is because of 2 popular techniques (James et al. 2014, P. Bruce and Bruce 2017):
-
- each of the tree randomly grabs a data subset from the input training dataset and averaging the models’ results, it is known as bagging or bootstrap aggregating) and,
-
- each of the tree will be given randomly a smaller number of variables for them to choose when they do their split in their nodes, it is known as bootstrap sampling.
set.seed(123)
model_rf <- train(house.value ~., data = train.data,
method = "rf",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3),
importance = T)
model_rf$finalModel##
## Call:
## randomForest(x = x, y = y, mtry = min(param$mtry, ncol(x)), importance = ..1)
## Type of random forest: regression
## Number of trees: 500
## No. of variables tried at each split: 7
##
## Mean of squared residuals: 14.1975
## % Var explained: 83.07
By default, 500 trees were grown to build the random forest model with their results averaged. The internal accuracy is 83.29%, which is considered very good. You will see a much better at 89.9% (or 90%) later when I predict on the test dataset.
The optimum number (mtry) of predictor variables randomly selected as variables of choice during each split is 7. Ths value is automatically discovered by the caret package.
model_rf$bestTune## mtry
## 2 7
The prediction result of this random forest model with the test data is:
# Make predictions
predictions <- model_rf %>% predict(test.data)
# Model performance
caret::R2(predictions, test.data$house.value)## [1] 0.9002483
caret::RMSE(predictions, test.data$house.value)## [1] 3.028622
Plotting the variance importance plot of random forest and having following result. This “importance” plot tells you which variables are importance in term of their predictive power in relative to each other. The higher the importance ranking of one variable in the importance plot, the higher its impact on the outcome variables. It is also associated with an increase in significance level (lower P-value).
plot(varImp(model_rf))This importance plot created by the random forest algorithm is useful in telling us how far the important features are away from the unimportant ones. I can see that “lstat” which is the proportion of lower status of the population in the community and the number of room by “room” are the two most important features in predicting the median house prices.
This result is the same as the results from multiple regression regression in previous section 5.2, check out following summary tabels.
options(scipen = 999)
summary(model_mlr)$coef %>%
data.frame() %>%
rename(P_Value = Pr...t..) %>%
arrange(P_Value) %>%
dplyr::select(Estimate, P_Value) %>%
mutate(Significance.ordered = case_when(P_Value < 0.05 & P_Value > 0.01 ~ "* (< 0.05)",
P_Value < 0.01 & P_Value > 0.001 ~ "** (< 0.01)",
P_Value < 0.001 ~ "*** (< 0.001)",
TRUE ~ " ")) %>%
arrange(P_Value) %>%
rownames_to_column(var = "features") %>%
mutate("no." = row_number()) %>%
relocate("no.", .before = features) %>%
filter(features != "(Intercept)",
Estimate > 0) %>%
kbl(caption = "Factors that Negatively Correlated with House Prices") %>%
kable_paper() | no. | features | Estimate | P\_Value | Significance.ordered |
|---|---|---|---|---|
| 2 | room | 3.6544550 | 0.0000000 | \*\*\* (< 0.001) |
| 6 | highway.index | 0.3252202 | 0.0000463 | \*\*\* (< 0.001) |
| 8 | black | 0.0109016 | 0.0003139 | \*\*\* (< 0.001) |
| 11 | charles.river1 | 2.3451853 | 0.0152888 |
|
| 12 | resid.zone | 0.0385636 | 0.0189201 |
|
| 14 | age | 0.0038368 | 0.8092879 |
options(scipen = 1)options(scipen = 999)
summary(model_mlr)$coef %>%
data.frame() %>%
rename(P_Value = Pr...t..) %>%
arrange(P_Value) %>%
dplyr::select(Estimate, P_Value) %>%
mutate(Significance.ordered = case_when(P_Value < 0.05 & P_Value > 0.01 ~ "* (< 0.05)",
P_Value < 0.01 & P_Value > 0.001 ~ "** (< 0.01)",
P_Value < 0.001 ~ "*** (< 0.001)",
TRUE ~ " ")) %>%
arrange(P_Value) %>%
rownames_to_column(var = "features") %>%
mutate("no." = row_number()) %>%
relocate("no.", .before = features) %>%
filter(features != "(Intercept)",
Estimate < 0) %>%
kbl(caption = "Factors that Negatively Correlated with House Prices") %>%
kable_paper() | no. | features | Estimate | P\_Value | Significance.ordered |
|---|---|---|---|---|
| 1 | lstat | -0.5092300 | 0.0000000 | \*\*\* (< 0.001) |
| 4 | pt.ratio | -0.9713006 | 0.0000000 | \*\*\* (< 0.001) |
| 5 | dist.to.work | -1.4195477 | 0.0000000 | \*\*\* (< 0.001) |
| 7 | nitrogen.oxide | -17.4399946 | 0.0001027 | \*\*\* (< 0.001) |
| 9 | property.tax | -0.0122952 | 0.0059351 | \*\* (< 0.01) |
| 10 | crime.rate | -0.0994196 | 0.0136800 |
|
| 13 | indus.biz | -0.0199231 | 0.7798097 |
options(scipen = 1)-
Importance plot shows that “room” is the most important variable, which is supported by multiple linear regression summary with indication that this relationship is negative.
-
Importance plot shows that “lstat” is the second most important variable, which is supported by multiple linear regression summary with indication that this relationship is positive.
The results of these two different algorithms usually are not the same. For example, the relationships between features and the responding variables in this project is non-linear and the result from multiple linear regression may not be so correct as compared to random forest that can digest non-linearity. Results from both algorithm could be similar (not entire the same) only if predictive power among features are really outcompete others in a significant way.
Variables “lstat” and “room” are instead supported by the results of the two different algorithms, and therefore it is robust to say “lstat” and “room” are the two most important features in the prediction of median house prices.
This section builds an alternative forest, known as “XGBoost”. Compared to random forest, many trees will also be grown in XGBoost “forest”. However, trees are now grown sequentially, one by one, by using information from previously grown trees with an aim to minimise the error from the previous models (James et al. 2014). Therefore, trees will become better and better with lesser and lesser error.
In the following, I am applying the caret package to combine with the xgboost package to automatically find the best tuning parameters and fit the final best boosted tree.
set.seed(123)
model_xgb <- train(house.value ~., data = train.data,
method = "xgbTree",
trControl = trainControl(method = "repeatedcv",
number = 10,
repeats = 3)
)This caret codes help to search a numbers of tuning parameters as shown below.
model_xgb## eXtreme Gradient Boosting
##
## 407 samples
## 13 predictor
##
## No pre-processing
## Resampling: Cross-Validated (10 fold, repeated 3 times)
## Summary of sample sizes: 366, 367, 366, 366, 366, 366, ...
## Resampling results across tuning parameters:
##
## eta max_depth colsample_bytree subsample nrounds RMSE Rsquared
## 0.3 1 0.6 0.50 50 4.182853 0.7854594
## 0.3 1 0.6 0.50 100 4.126536 0.7908102
## 0.3 1 0.6 0.50 150 4.161106 0.7861019
## 0.3 1 0.6 0.75 50 4.142924 0.7897273
## 0.3 1 0.6 0.75 100 4.107600 0.7933788
## 0.3 1 0.6 0.75 150 4.120252 0.7913811
## 0.3 1 0.6 1.00 50 4.151153 0.7882856
## 0.3 1 0.6 1.00 100 4.116424 0.7920502
## 0.3 1 0.6 1.00 150 4.124839 0.7913928
## 0.3 1 0.8 0.50 50 4.157485 0.7903991
## 0.3 1 0.8 0.50 100 4.079975 0.7969387
## 0.3 1 0.8 0.50 150 4.048677 0.7988566
## 0.3 1 0.8 0.75 50 4.150224 0.7874679
## 0.3 1 0.8 0.75 100 4.199768 0.7820608
## 0.3 1 0.8 0.75 150 4.195123 0.7827416
## 0.3 1 0.8 1.00 50 4.131791 0.7888757
## 0.3 1 0.8 1.00 100 4.129239 0.7892943
## 0.3 1 0.8 1.00 150 4.128452 0.7898088
## 0.3 2 0.6 0.50 50 3.777177 0.8222663
## 0.3 2 0.6 0.50 100 3.675503 0.8311953
## 0.3 2 0.6 0.50 150 3.667622 0.8318334
## 0.3 2 0.6 0.75 50 3.763559 0.8208369
## 0.3 2 0.6 0.75 100 3.669985 0.8274995
## 0.3 2 0.6 0.75 150 3.608987 0.8333291
## 0.3 2 0.6 1.00 50 3.746535 0.8235279
## 0.3 2 0.6 1.00 100 3.618285 0.8333832
## 0.3 2 0.6 1.00 150 3.586081 0.8353849
## 0.3 2 0.8 0.50 50 3.762808 0.8216546
## 0.3 2 0.8 0.50 100 3.587117 0.8371032
## 0.3 2 0.8 0.50 150 3.556984 0.8390137
## 0.3 2 0.8 0.75 50 3.595348 0.8402412
## 0.3 2 0.8 0.75 100 3.446987 0.8525955
## 0.3 2 0.8 0.75 150 3.432346 0.8537018
## 0.3 2 0.8 1.00 50 3.723154 0.8225154
## 0.3 2 0.8 1.00 100 3.639498 0.8286580
## 0.3 2 0.8 1.00 150 3.593235 0.8325319
## 0.3 3 0.6 0.50 50 3.610050 0.8380176
## 0.3 3 0.6 0.50 100 3.546845 0.8426869
## 0.3 3 0.6 0.50 150 3.553873 0.8426153
## 0.3 3 0.6 0.75 50 3.629149 0.8367095
## 0.3 3 0.6 0.75 100 3.596844 0.8382378
## 0.3 3 0.6 0.75 150 3.589758 0.8382567
## 0.3 3 0.6 1.00 50 3.572412 0.8393511
## 0.3 3 0.6 1.00 100 3.539100 0.8416870
## 0.3 3 0.6 1.00 150 3.540782 0.8413578
## 0.3 3 0.8 0.50 50 3.764554 0.8255141
## 0.3 3 0.8 0.50 100 3.746043 0.8260430
## 0.3 3 0.8 0.50 150 3.733853 0.8267933
## 0.3 3 0.8 0.75 50 3.645393 0.8317390
## 0.3 3 0.8 0.75 100 3.606017 0.8342552
## 0.3 3 0.8 0.75 150 3.612220 0.8336288
## 0.3 3 0.8 1.00 50 3.472483 0.8494223
## 0.3 3 0.8 1.00 100 3.430406 0.8519789
## 0.3 3 0.8 1.00 150 3.423115 0.8525365
## 0.4 1 0.6 0.50 50 4.242024 0.7809725
## 0.4 1 0.6 0.50 100 4.176060 0.7868365
## 0.4 1 0.6 0.50 150 4.151872 0.7873821
## 0.4 1 0.6 0.75 50 4.228494 0.7852974
## 0.4 1 0.6 0.75 100 4.205671 0.7837945
## 0.4 1 0.6 0.75 150 4.231413 0.7795390
## 0.4 1 0.6 1.00 50 4.189509 0.7830316
## 0.4 1 0.6 1.00 100 4.131326 0.7880123
## 0.4 1 0.6 1.00 150 4.140639 0.7873879
## 0.4 1 0.8 0.50 50 4.233230 0.7819111
## 0.4 1 0.8 0.50 100 4.155860 0.7884511
## 0.4 1 0.8 0.50 150 4.195970 0.7866299
## 0.4 1 0.8 0.75 50 4.162934 0.7889422
## 0.4 1 0.8 0.75 100 4.151237 0.7888796
## 0.4 1 0.8 0.75 150 4.165509 0.7865194
## 0.4 1 0.8 1.00 50 4.147841 0.7866652
## 0.4 1 0.8 1.00 100 4.138036 0.7883324
## 0.4 1 0.8 1.00 150 4.117973 0.7905922
## 0.4 2 0.6 0.50 50 3.826323 0.8168702
## 0.4 2 0.6 0.50 100 3.780867 0.8187857
## 0.4 2 0.6 0.50 150 3.719562 0.8236568
## 0.4 2 0.6 0.75 50 3.682837 0.8313142
## 0.4 2 0.6 0.75 100 3.589292 0.8377619
## 0.4 2 0.6 0.75 150 3.575998 0.8386209
## 0.4 2 0.6 1.00 50 3.806052 0.8132234
## 0.4 2 0.6 1.00 100 3.714299 0.8207919
## 0.4 2 0.6 1.00 150 3.670559 0.8244077
## 0.4 2 0.8 0.50 50 3.776071 0.8227278
## 0.4 2 0.8 0.50 100 3.755586 0.8253629
## 0.4 2 0.8 0.50 150 3.740228 0.8269079
## 0.4 2 0.8 0.75 50 3.625007 0.8351658
## 0.4 2 0.8 0.75 100 3.508651 0.8451157
## 0.4 2 0.8 0.75 150 3.493164 0.8460368
## 0.4 2 0.8 1.00 50 3.689192 0.8295638
## 0.4 2 0.8 1.00 100 3.604157 0.8355012
## 0.4 2 0.8 1.00 150 3.584599 0.8370836
## 0.4 3 0.6 0.50 50 3.910812 0.8171158
## 0.4 3 0.6 0.50 100 3.894401 0.8176998
## 0.4 3 0.6 0.50 150 3.868580 0.8195093
## 0.4 3 0.6 0.75 50 3.612758 0.8358911
## 0.4 3 0.6 0.75 100 3.617881 0.8349569
## 0.4 3 0.6 0.75 150 3.621635 0.8349276
## 0.4 3 0.6 1.00 50 3.558495 0.8408873
## 0.4 3 0.6 1.00 100 3.547564 0.8414694
## 0.4 3 0.6 1.00 150 3.546732 0.8416371
## 0.4 3 0.8 0.50 50 3.766353 0.8249109
## 0.4 3 0.8 0.50 100 3.769196 0.8223233
## 0.4 3 0.8 0.50 150 3.776131 0.8219151
## 0.4 3 0.8 0.75 50 3.587272 0.8369683
## 0.4 3 0.8 0.75 100 3.586344 0.8371400
## 0.4 3 0.8 0.75 150 3.593978 0.8369866
## 0.4 3 0.8 1.00 50 3.504237 0.8481865
## 0.4 3 0.8 1.00 100 3.518748 0.8461964
## 0.4 3 0.8 1.00 150 3.529298 0.8450712
## MAE
## 2.900754
## 2.803454
## 2.806837
## 2.841964
## 2.769818
## 2.741878
## 2.861273
## 2.788297
## 2.759423
## 2.895077
## 2.799370
## 2.755008
## 2.853392
## 2.826829
## 2.790949
## 2.843929
## 2.786062
## 2.759977
## 2.641128
## 2.567048
## 2.530043
## 2.588745
## 2.497320
## 2.464712
## 2.545620
## 2.444827
## 2.416717
## 2.605044
## 2.495232
## 2.475766
## 2.477564
## 2.372487
## 2.357415
## 2.517459
## 2.425566
## 2.388926
## 2.530563
## 2.480395
## 2.493422
## 2.461517
## 2.430207
## 2.422150
## 2.400758
## 2.373322
## 2.385540
## 2.579637
## 2.565885
## 2.576543
## 2.486560
## 2.458141
## 2.458571
## 2.390172
## 2.352385
## 2.352459
## 2.978555
## 2.878119
## 2.838157
## 2.916006
## 2.829245
## 2.803125
## 2.877125
## 2.788637
## 2.757291
## 2.984032
## 2.875600
## 2.862312
## 2.917135
## 2.830734
## 2.803543
## 2.878896
## 2.827634
## 2.795371
## 2.660083
## 2.606812
## 2.578052
## 2.567962
## 2.523099
## 2.519504
## 2.567428
## 2.492046
## 2.464206
## 2.607522
## 2.592710
## 2.590052
## 2.520089
## 2.432883
## 2.416543
## 2.493979
## 2.421174
## 2.411651
## 2.701700
## 2.713348
## 2.705727
## 2.503308
## 2.520742
## 2.522791
## 2.434217
## 2.428093
## 2.428280
## 2.621254
## 2.624871
## 2.617245
## 2.413185
## 2.426654
## 2.441374
## 2.414667
## 2.427397
## 2.440096
##
## Tuning parameter 'gamma' was held constant at a value of 0
## Tuning
## parameter 'min_child_weight' was held constant at a value of 1
## RMSE was used to select the optimal model using the smallest value.
## The final values used for the model were nrounds = 150, max_depth = 3, eta
## = 0.3, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1 and subsample
## = 1.
The final values used for the model were nrounds = 100, max_depth = 3, eta = 0.4, gamma = 0, colsample_bytree = 0.8, min_child_weight = 1 and subsample = 1.
model_xgb$bestTune## nrounds max_depth eta gamma colsample_bytree min_child_weight subsample
## 54 150 3 0.3 0 0.8 1 1
Making prediction on the test data using this xgb_model.
# predictions
predictions <- model_xgb %>% predict(test.data)
# model performance
caret::R2(predictions, test.data$house.value)## [1] 0.9007896
caret::RMSE(predictions, test.data$house.value)## [1] 2.97001
This model has results that are not too far away from random forest. Next section will create a graph to compare the performance metrics of all machine learning models I have trained.
# set up dataframe
Model <- c("Lasso",
"PLS",
"KNN",
"Decision Tree",
"Random Forest",
"XGBoost")
R2_value <- c(0.7652148,
0.7687147,
0.8841925,
0.7953629,
0.8996801,
0.8844266)
RMSE_value <- c(4.663365,
4.531626,
3.46252,
4.217293,
3.038207,
3.190433
)
models <- data.frame(Model, R2_value, RMSE_value)
models <- models %>%
mutate(R2_percentage = round(R2_value*100, 2),
Error_rate_percent = RMSE_value/mean(test.data$house.value),
Error_rate_percent = round(Error_rate_percent * 100,2)) %>%
pivot_longer(c(4:5), names_to = "metrics", values_to = "results") %>%
mutate(Model = reorder_within(x = Model, by = results, within = metrics))
# plot
ggplot(models, aes(x = fct_reorder(Model, -results), y = results, fill = metrics)) +
geom_bar(stat = "identity") +
facet_wrap(~metrics, scale = "free_x") +
theme_bw() +
theme(legend.position = "none",
axis.text.x = element_text(angle = 10),
plot.title = element_text(face = "bold")) +
scale_x_reordered() +
labs(x = "Models",
y = "%",
title = "Comparing Performance Metrics of All ML Models") +
geom_text(aes(label = paste0(results, "%"), vjust = 1.5))From this result, I conclude that random forest algorithm has the highest prediction performance on the randomly sampled test dataset in this project. It has the highest good R-squared value (R2, %) at 89.97%, or 90%.
The 89.97% R-squared value means that the predicted outcome values by the Random Forest using the test dataset has a high correlation with the observed values in the test dataset. Alternatively, results are approximately 90% similar. Random forest has also the lowest prediction error rate at 13.43% (RMSE divided by the mean of the y variables in test dataset).
This section uses RShiny to produce an online interactive application to make predictions using the random forest algorithm.
Demo picture:
Visit this link to use the app:
https://karhou.shinyapps.io/boston/
Visit this github link to view the codes I used to program this app.
https://github.com/KAR-NG/Predicting-House-Prices-in-Boston_UniqueVersion/blob/main/app.R
In conclusion, 7 different models were built to study this dataset, included multiple linear regression (MLR), Lasso regression, Partial Least Squares (PLS), K-Nearest Neighbor (KNN), Decision tree, random forest, and stochastic gradient boosted random forest (XGBoost).
-
Random forest model had the best predictive power at 90% compared to all other models and should be used for prediction. A RShiny app has been built to make this model into production.
-
The variable “age” that stands for “Proportion of owner-occupied units built prior to 1940” and the variable “indus” that stands for “Proportion of non-retail business acres per town” are not related in the house prices with P higher than 0.05.
-
The 3 most positively related variables are the number of rooms that affects house prices the most with the most significance level (lowest P-value with a value of < 0.001), followed by the proportion of black community (P-value <0.001) and the index of accessibility to radial highway (P-value <0.001).
-
The 3 most negatively related variables are the lower status of the population (percent) (P-value <0.001), followed by the second ranked nitrogen oxide concentration (P-value <0.001), and the third negative variable is crime rate (P-value < 0.05). The higher the values of these variables, house prices are negatively impacted the most.
-
In overall, the most important 2 variables related to the Boston median house prices in the late 70s are the number of room (positive related) and the proportion of lower status population in the community (negative related).
Thank you for reading
The purpose of this project is for educational and skills demonstration ONLY.
Boston thumbnail picture By King of Hearts - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=62981160
Belsley D.A., Kuh, E. and Welsch, R.E. (1980) Regression Diagnostics. Identifying Influential Data and Sources of Collinearity. New York: Wiley.
Brownlee J 2016, How to Work Through a Regression Machine Learning Project in Weka, viewed 26 September 2021, https://machinelearningmastery.com/regression-machine-learning-tutorial-weka/
Data Professor 2020, Web Apps in R: Building the Machine Learning Web Application in R | Shiny Tutorial Ep 4, viewed 4 October 2021, https://www.youtube.com/watch?v=ceg7MMQNln8&t=847s
Harrison, D. and Rubinfeld, D.L. (1978) Hedonic prices and the demand for clean air. J. Environ. Economics and Management 5, 81–102.
James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. 2014. An Introduction to Statistical Learning: With Applications in R . Springer Publishing Company, Incorporated.
Minitab Blog Editor 2013, Enough Is Enough! Handling Multicollinearity in Regression Analysis, viewed 25 September 2021, https://blog.minitab.com/en/understanding-statistics/handling-multicollinearity-in-regression-analysis
Sivakumar C 2017, https://rpubs.com/chocka314/251613, viewed 28 September 2021, https://rpubs.com/chocka314/251613