-
Notifications
You must be signed in to change notification settings - Fork 1
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
estimate win rate (pure theoretical by math computations) #26
Comments
|
for more round than r, for example draw 4 tiles to get (4s,5s) in (3*4s,2*5s,otherwise*70) invisible, we could:
Since P(1s,2s) is dependent to P(3s,4s) while r>2, Inclusion–exclusion Principle should be used to calculate precise probability.
MultiNomial equally estimation can also be adjusted by analysis other's player hand based on discarded tiles. |
|
consider that pick away tiles influence the remain tiles, we could directly use combinitions to calculate classical probability, then directly use Gamma function to get a general result for real-numbers remain tile estimation (adjust distribution by other's player hand by directly add tile expection to invisible tile) |
|
we could divide it by define "useful-tiles" (u1,u2,u3,..un), "otherwise" to get a clean division. then enumerate on u by restrition sum(ui) <= r and each ui <= invisible-ui |
|
Another idea is making this a 0-1 Knapsack Problem (counting combinitions) by mapping volumn to remain tiles to choose, mapping tiles to weights-values, add restriction below: mactch at least a useful set lead to win (i.e. '4s5s1z' in 6s123m456789p1z7z) this could be achieved by some common sequence dynamic programming, or something like AC-machine to represent state like
then apply something like O(n^3) dynamic-programming algorithms (which is acceptable since n<=136, the total tiles in mahjong) to find the answer. |
Since here we could get all possible combination for win:
auto-white-reimu/mahjong/container/pattern/reasoning.py
Line 169 in 90f0020
assume each invisible tile is equal probability, we could leverage multinomial distribution for given a possible combination with r tiles in the invisible set: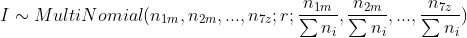
like wikipedia explained,
we could directly get all possible combinition probability just simply sum the pmf of each combination
here.
The text was updated successfully, but these errors were encountered: