diff --git a/docs/index.md b/docs/index.md index ee0323919..0f092ab76 100644 --- a/docs/index.md +++ b/docs/index.md @@ -8,152 +8,48 @@ ./README.md:description --8<-- -## 📝案例列表 - - - -

数学(AI for Math)

- -| 问题类型 | 案例名称 | 优化算法 | 模型类型 | 训练方式 | 数据集 | 参考资料 | -|-----|---------|-----|---------|----|---------|---------| -| 微分方程 | [拉普拉斯方程](./zh/examples/laplace2d.md) | 机理驱动 | MLP | 无监督学习 | - | - | -| 微分方程 | [伯格斯方程](./zh/examples/deephpms.md) | 机理驱动 | MLP | 无监督学习 | [Data](https://github.com/maziarraissi/DeepHPMs/tree/master/Data) | [Paper](https://arxiv.org/pdf/1801.06637.pdf) | -| 微分方程 | [洛伦兹方程](./zh/examples/lorenz.md) | 数据驱动 | Transformer-Physx | 监督学习 | [Data](https://github.com/zabaras/transformer-physx) | [Paper](https://arxiv.org/abs/2010.03957) | -| 微分方程 | [若斯叻方程](./zh/examples/rossler.md) | 数据驱动 | Transformer-Physx | 监督学习 | [Data](https://github.com/zabaras/transformer-physx) | [Paper](https://arxiv.org/abs/2010.03957) | -| 算子学习 | [DeepONet](./zh/examples/deeponet.md) | 数据驱动 | MLP | 监督学习 | [Data](https://deepxde.readthedocs.io/en/latest/demos/operator/antiderivative_unaligned.html) | [Paper](https://export.arxiv.org/pdf/1910.03193.pdf) | -| 微分方程 | 梯度增强的物理知识融合PDE求解coming soon | 机理驱动 | gPINN | 半监督学习 | - | [Paper](https://www.sciencedirect.com/science/article/abs/pii/S0045782522001438?via%3Dihub) | -| 积分方程 | [沃尔泰拉积分方程](./zh/examples/volterra_ide.md) | 机理驱动 | MLP | 无监督学习 | - | [Project](https://github.com/lululxvi/deepxde/blob/master/examples/pinn_forward/Volterra_IDE.py) | - -
-

技术科学(AI for Technology)

- -| 问题类型 | 案例名称 | 优化算法 | 模型类型 | 训练方式 | 数据集 | 参考资料 | -|-----|---------|-----|---------|----|---------|---------| -| 定常不可压流体 | [2D 定常方腔流](./zh/examples/ldc2d_steady.md) | 机理驱动 | MLP | 无监督学习 | - | | -| 定常不可压流体 | [2D 达西流](./zh/examples/darcy2d.md) | 机理驱动 | MLP | 无监督学习 | - | | -| 定常不可压流体 | [2D 管道流](./zh/examples/labelfree_DNN_surrogate.md) | 机理驱动 | MLP | 无监督学习 | - | [Paper](https://arxiv.org/abs/1906.02382) | -| 定常不可压流体 | [3D 血管瘤](./zh/examples/aneurysm.md) | 机理驱动 | MLP | 无监督学习 | [Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/aneurysm/aneurysm_dataset.tar) | [Project](https://docs.nvidia.com/deeplearning/modulus/modulus-v2209/user_guide/intermediate/adding_stl_files.html)| -| 定常不可压流体 | [任意 2D 几何体绕流](./zh/examples/deepcfd.md) | 数据驱动 | DeepCFD | 监督学习 | - | [Paper](https://arxiv.org/abs/2004.08826)| -| 非定常不可压流体 | [2D 非定常方腔流](./zh/examples/ldc2d_unsteady.md) | 机理驱动 | MLP | 无监督学习 | - | -| -| 非定常不可压流体 | [Re100 2D 圆柱绕流](./zh/examples/cylinder2d_unsteady.md) | 机理驱动 | MLP | 半监督学习 | [Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/cylinder2d_unsteady_Re100/cylinder2d_unsteady_Re100_dataset.tar) | [Paper](https://arxiv.org/abs/2004.08826)| -| 非定常不可压流体 | [Re100~750 2D 圆柱绕流](./zh/examples/cylinder2d_unsteady_transformer_physx.md) | 数据驱动 | Transformer-Physx | 监督学习 | [Data](https://github.com/zabaras/transformer-physx) | [Paper](https://arxiv.org/abs/2010.03957)| -| 可压缩流体 | [2D 空气激波](./zh/examples/shock_wave.md) | 机理驱动 | PINN-WE | 无监督学习 | - | [Paper](https://arxiv.org/abs/2206.03864)| -| 流固耦合 | [涡激振动](./zh/examples/viv.md) | 机理驱动 | MLP | 半监督学习 | [Data](https://github.com/PaddlePaddle/PaddleScience/blob/develop/examples/fsi/VIV_Training_Neta100.mat) | [Paper](https://arxiv.org/abs/2206.03864)| -| 多相流 | [气液两相流](./zh/examples/bubble.md) | 机理驱动 | BubbleNet | 半监督学习 | [Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat) | [Paper](https://pubs.aip.org/aip/adv/article/12/3/035153/2819394/Predicting-micro-bubble-dynamics-with-semi-physics)| -| 多相流 | [twophasePINN](https://aistudio.baidu.com/projectdetail/5379212) | 机理驱动 | MLP | 无监督学习 | - | [Paper](https://doi.org/10.1016/j.mlwa.2021.100029)| -| 多相流 | 非高斯渗透率场估计coming soon | 机理驱动 | cINN | 监督学习 | - | [Paper](https://pubs.aip.org/aip/adv/article/12/3/035153/2819394/Predicting-micro-bubble-dynamics-with-semi-physics)| -| 流场高分辨率重构 | [2D 湍流流场重构](./docs/zh/examples/tempoGAN.md) | 数据驱动 | tempoGAN | 监督学习 | [Train Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat)
[Eval Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat) | [Paper](https://dl.acm.org/doi/10.1145/3197517.3201304)| -| 流场高分辨率重构 | [2D 湍流流场重构](https://aistudio.baidu.com/projectdetail/4493261?contributionType=1) | 数据驱动 | cycleGAN | 监督学习 | [Train Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat)
[Eval Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat) | [Paper](https://arxiv.org/abs/2007.15324)| -| 流场高分辨率重构 | [基于Voronoi嵌入辅助深度学习的稀疏传感器全局场重建](https://aistudio.baidu.com/projectdetail/5807904) | 数据驱动 | CNN | 监督学习 | [Data1](https://drive.google.com/drive/folders/1K7upSyHAIVtsyNAqe6P8TY1nS5WpxJ2c)
[Data2](https://drive.google.com/drive/folders/1pVW4epkeHkT2WHZB7Dym5IURcfOP4cXu)
[Data3](https://drive.google.com/drive/folders/1xIY_jIu-hNcRY-TTf4oYX1Xg4_fx8ZvD) | [Paper](https://arxiv.org/pdf/2202.11214.pdf) | -| 流场高分辨率重构 | 基于扩散的流体超分重构coming soon | 数理融合 | DDPM | 监督学习 | - | [Paper](https://www.sciencedirect.com/science/article/pii/S0021999123000670)| -| 受力分析 | [1D 欧拉梁变形](../examples/euler_beam/euler_beam.py) | 机理驱动 | MLP | 无监督学习 | - | - | -| 受力分析 | [2D 平板变形](https://aistudio.baidu.com/aistudio/projectdetail/5792325) | 机理驱动 | MLP | 无监督学习 | - | - | -| 受力分析 | [3D 连接件变形](./zh/examples/bracket.md) | 机理驱动 | MLP | 无监督学习 | [Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/bracket/bracket_dataset.tar) | [Tutorial](https://docs.nvidia.com/deeplearning/modulus/modulus-v2209/user_guide/foundational/linear_elasticity.html) | -| 受力分析 | [结构震动模拟](./zh/examples/phylstm.md) | 机理驱动 | PhyLSTM | 监督学习 | [Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/PhyLSTM/data_boucwen.mat) | [Paper](https://arxiv.org/abs/2002.10253) | - -
-

材料科学(AI for Material)

- -| 问题类型 | 案例名称 | 优化算法 | 模型类型 | 训练方式 | 数据集 | 参考资料 | -|-----|---------|-----|---------|----|---------|---------| -| 材料设计 | [散射板设计(反问题)](./zh/examples/hpinns.md) | 数理融合 | 数据驱动 | 监督学习 | [Train Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_train.mat)
[Eval Data](https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_valid.mat) | [Paper](https://arxiv.org/pdf/2102.04626.pdf) | -| 材料生成 | 面向对称感知的周期性材料生成coming soon | 数据驱动 | SyMat | 监督学习 | - | - | - -
-

地球科学(AI for Earth Science)

- -| 问题类型 | 案例名称 | 优化算法 | 模型类型 | 训练方式 | 数据集 | 参考资料 | -|-----|---------|-----|---------|----|---------|---------| -| 天气预报 | [FourCastNet 气象预报](./zh/examples/fourcastnet.md) | 数据驱动 | FourCastNet | 监督学习 | [ERA5](https://app.globus.org/file-manager?origin_id=945b3c9e-0f8c-11ed-8daf-9f359c660fbd&origin_path=%2F~%2Fdata%2F) | [Paper](https://arxiv.org/pdf/2202.11214.pdf) | -| 天气预报 | GraphCast 气象预报coming soon | 数据驱动 | GraphCastNet* | 监督学习 | - | [Paper](https://arxiv.org/abs/2212.12794) | -| 大气污染物 | [UNet 污染物扩散](https://aistudio.baidu.com/projectdetail/5663515?channel=0&channelType=0&sUid=438690&shared=1&ts=1698221963752) | 数据驱动 | UNet | 监督学习 | [Data](https://aistudio.baidu.com/datasetdetail/198102) | - | - -## 🚀快速安装 - -=== "方式1: 源码安装[推荐]" - - --8<-- - ./README.md:git_install - --8<-- - -=== "方式2: pip安装" - - ``` shell - pip install paddlesci - ``` - -=== "[完整安装流程](./zh/install_setup.md)" - - ``` shell - pip install paddlesci - ``` - - ``` shell - pip install paddlesci - ``` +![panorama](https://paddle-org.bj.bcebos.com/paddlescience/docs/overview/panorama.png) + +!!! tip "快速安装" + + === "方式1: 源码安装[推荐]" + + --8<-- + ./README.md:git_install + --8<-- + + === "方式2: pip安装" + + ``` shell + pip install paddlesci + ``` + + === "[完整安装流程](./zh/install_setup.md)" + + ``` shell + pip install paddlesci + ``` --8<-- -./README.md:feature +./README.md:update --8<-- --8<-- -./README.md:support +./README.md:feature --8<-- --8<-- -./README.md:contribution +./README.md:support --8<-- --8<-- -./README.md:collaboration +./README.md:contribution --8<-- --8<-- ./README.md:thanks --8<-- -- PaddleScience 的部分代码由以下优秀社区开发者贡献（按 [Contributors](https://github.com/PaddlePaddle/PaddleScience/graphs/contributors) 排序）： - - - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - avatar - ---8<-- -./README.md:cooperation ---8<-- - --8<-- ./README.md:license --8<-- diff --git a/docs/zh/api/arch.md b/docs/zh/api/arch.md index 03e4f6253..30358350e 100644 --- a/docs/zh/api/arch.md +++ b/docs/zh/api/arch.md @@ -7,7 +7,6 @@ - Arch - MLP - DeepONet - - DeepPhyLSTM - LorenzEmbedding - RosslerEmbedding - CylinderEmbedding @@ -17,6 +16,5 @@ - ModelList - AFNONet - PrecipNet - - UNetEx show_root_heading: false heading_level: 3 diff --git a/docs/zh/api/data/dataset.md b/docs/zh/api/data/dataset.md index 96e64da56..f2e8f0708 100644 --- a/docs/zh/api/data/dataset.md +++ b/docs/zh/api/data/dataset.md @@ -1,4 +1,4 @@ -# Data.dataset(数据集) 模块 +# Data(数据) 模块 ::: ppsci.data.dataset handler: python @@ -16,6 +16,4 @@ - LorenzDataset - RosslerDataset - VtuDataset - - MeshAirfoilDataset - - MeshCylinderDataset show_root_heading: false diff --git a/docs/zh/api/data/process/batch_transform.md b/docs/zh/api/data/process/batch_transform.md index 4121821ee..fa3b426e6 100644 --- a/docs/zh/api/data/process/batch_transform.md +++ b/docs/zh/api/data/process/batch_transform.md @@ -1 +1 @@ -# Data.batch_transform(批预处理) 模块 +# Batch Transform(批预处理) 模块 diff --git a/docs/zh/api/data/process/transform.md b/docs/zh/api/data/process/transform.md index 78647df16..3e7f511c6 100644 --- a/docs/zh/api/data/process/transform.md +++ b/docs/zh/api/data/process/transform.md @@ -1,4 +1,4 @@ -# Data.transform(预处理) 模块 +# Transform(预处理) 模块 ::: ppsci.data.process.transform handler: python @@ -10,5 +10,4 @@ - Log1p - CropData - SqueezeData - - FunctionalTransform show_root_heading: false diff --git a/docs/zh/api/lr_scheduler.md b/docs/zh/api/lr_scheduler.md index 8de28be5b..8dfae5a6c 100644 --- a/docs/zh/api/lr_scheduler.md +++ b/docs/zh/api/lr_scheduler.md @@ -1,4 +1,4 @@ -# Optimizer.lr_scheduler(学习率) 模块 +# Lr_scheduler(学习率) 模块 ::: ppsci.optimizer.lr_scheduler handler: python diff --git a/docs/zh/api/optimizer.md b/docs/zh/api/optimizer.md index d220b82a9..6bb0e0e9c 100644 --- a/docs/zh/api/optimizer.md +++ b/docs/zh/api/optimizer.md @@ -1,4 +1,4 @@ -# Optimizer.optimizer(优化器) 模块 +# Optimizer(优化器) 模块 ::: ppsci.optimizer.optimizer handler: python diff --git a/docs/zh/api/utils.md b/docs/zh/api/utils.md new file mode 100644 index 000000000..8ce7878a3 --- /dev/null +++ b/docs/zh/api/utils.md @@ -0,0 +1,24 @@ +# Utils(工具) 模块 + +::: ppsci.utils + handler: python + options: + members: + - initializer + - logger + - misc + - load_csv_file + - load_mat_file + - load_vtk_file + - run_check + - profiler + - AttrDict + - ExpressionSolver + - AverageMeter + - set_random_seed + - load_checkpoint + - load_pretrain + - save_checkpoint + - lambdify + show_root_heading: false + heading_level: 3 diff --git a/docs/zh/development.md b/docs/zh/development.md index 8204d1c6b..4ceeb4763 100644 --- a/docs/zh/development.md +++ b/docs/zh/development.md @@ -1,58 +1,48 @@ # 开发指南 -本文档介绍如何基于 PaddleScience 套件进行代码开发并最终贡献到 PaddleScience 套件中。 - -PaddleScience 相关的论文复现、API 开发任务开始之前需提交 RFC 文档，请参考：[PaddleScience RFC Template](https://github.com/PaddlePaddle/community/blob/master/rfcs/Science/template.md) +本文档介绍如何基于 PaddleScience 套件进行代码开发并最终贡献到 PaddleScience 套件中 ## 1. 准备工作 -1. 将 PaddleScience fork 到**自己的仓库** -2. 克隆**自己仓库**里的 PaddleScience 到本地，并进入该目录 +1. 将 PaddleScience fork 到自己的仓库 +2. 克隆自己仓库里的 PaddleScience 到本地，并进入该目录 ``` sh - git clone -b develop https://github.com/USER_NAME/PaddleScience.git + git clone https://github.com/your_username/PaddleScience.git cd PaddleScience ``` - 上方 `clone` 命令中的 `USER_NAME` 字段请填入的自己的用户名。 - 3. 安装必要的依赖包 ``` sh - pip install -r requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple + pip install -r requirements.txt + # 安装较慢时可以加上-i选项，提升下载速度 + # pip install -r requirements.txt -i https://pypi.douban.com/simple/ ``` -4. 基于当前所在的 `develop` 分支，新建一个分支(假设新分支名字为 `dev_model`) +4. 基于 develop 分支，新建一个新分支(假设新分支名字为dev_model) ``` sh git checkout -b "dev_model" ``` -5. 添加 PaddleScience 目录到系统环境变量 `PYTHONPATH` 中 +5. 添加 PaddleScience 目录到系统环境变量 PYTHONPATH 中 ``` sh export PYTHONPATH=$PWD:$PYTHONPATH ``` -6. 执行以下代码，验证安装的 PaddleScience 基础功能是否正常 - - ``` sh - python -c "import ppsci; ppsci.run_check()" - ``` - - 如果出现 PaddleScience is installed successfully.✨ 🍰 ✨，则说明安装验证成功。 - ## 2. 编写代码 -完成上述准备工作后，就可以基于 PaddleScience 开始开发自己的案例或者功能了。 - -假设新建的案例代码文件路径为：`PaddleScience/examples/demo/demo.py`，接下来开始详细介绍这一流程 +完成上述准备工作后，就可以基于 PaddleScience 提供的 API 开始编写自己的案例代码了，接下来开始详细介绍 +这一过程。 ### 2.1 导入必要的包 -PaddleScience 所提供的 API 全部在 `ppsci.*` 模块下，因此在 `demo.py` 的开头首先需要导入 `ppsci` 这个顶层模块，接着导入日志打印模块 `logger`，方便打印日志时自动记录日志到本地文件中，最后再根据您自己的需要，导入其他必要的模块。 +PaddleScience 所提供的 API 全部在 `ppsci` 模块下，因此在代码文件的开头首先需要导入 `ppsci` 这个顶 +层模块以及日志打印模块，然后再根据您自己的需要，导入其他必要的模块。 -``` py title="examples/demo/demo.py" +``` py linenums="1" import ppsci from ppsci.utils import logger @@ -62,75 +52,59 @@ from ppsci.utils import logger ### 2.2 设置运行环境 -在运行 `demo.py` 之前，需要进行一些必要的运行环境设置，如固定随机种子(保证实验可复现性)、设置输出目录并初始化日志打印模块(保存重要实验数据)。 +在运行 python 的主体代码之前，我们同样需要设置一些必要的运行环境，比如固定随机种子、设置模型/日志保存 +目录、初始化日志打印模块。 -``` py title="examples/demo/demo.py" +``` py linenums="1" if __name__ == "__main__": # set random seed for reproducibility ppsci.utils.misc.set_random_seed(42) # set output directory - OUTPUT_DIR = "./output_example" + output_dir = "./output_example" # initialize logger - logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + logger.init_logger("ppsci", f"{output_dir}/train.log", "info") ``` -完成上述步骤之后，`demo.py` 已经搭好了必要框架。接下来介绍如何基于自己具体的需求，对 `ppsci.*` 下的其他模块进行开发或者复用，以最终在 `demo.py` 中使用。 - ### 2.3 构建模型 #### 2.3.1 构建已有模型 -PaddleScience 内置了一些常见的模型，如 `MLP` 模型，如果您想使用这些内置的模型，可以直接调用 [`ppsci.arch.*`](./api/arch.md) 下的 API，并填入模型实例化所需的参数，即可快速构建模型。 +PaddleScience 内置了一些常见的模型，如 `MLP` 模型，如果您想使用这些内置的模型，可以直接调用 +[`ppsci.arch`](./api/arch.md) 下的 API，并填入模型实例化所需的参数，即可快速构建模型。 -``` py title="examples/demo/demo.py" +``` py linenums="1" # create a MLP model model = ppsci.arch.MLP(("x", "y"), ("u", "v", "p"), 9, 50, "tanh") ``` -上述代码实例化了一个 `MLP` 全连接模型，其输入数据为两个字段：`"x"`、`"y"`，输出数据为三个字段：`"u"`、`"v"`、`"w"`；模型具有 $9$ 层隐藏层，每层的神经元个数为 $50$ 个，每层隐藏层使用的激活函数均为 $\tanh$ 双曲正切函数。 - #### 2.3.2 构建新的模型 -当 PaddleScience 内置的模型无法满足您的需求时，您就可以通过新增模型文件并编写模型代码的方式，使用您自定义的模型，步骤如下： +当 PaddleScienc 内置的模型无法满足您的需求时，您也可以通过新增模型文件并编写模型代码的方式，使用您自 +定义的模型，步骤如下： -1. 在 `ppsci/arch/` 文件夹下新建模型结构文件，以 `new_model.py` 为例。 -2. 在 `new_model.py` 文件中导入 PaddleScience 的模型基类所在的模块 `base`，并从 `base.Arch` 派生出您想创建的新模型类（以 -`Class NewModel` 为例）。 +1. 在 `ppsci/arch` 下新建模型结构文件，以 `new_model.py` 为例 +2. 在 `new_model.py` 文件中导入 PaddleScience 的模型基类所在模块 `base`，并让创建的新模型类（以 +`Class NewModel` 为例）从 `base.Arch` 继承。 - ``` py title="ppsci/arch/new_model.py" + ``` py linenums="1" title="ppsci/arch/new_model.py" from ppsci.arch import base class NewModel(base.Arch): def __init__(self, ...): ... - # initialization + # init def forward(self, ...): ... # forward ``` -3. 编写 `NewModel.__init__` 方法，其被用于模型创建时的初始化操作，包括模型层、参数变量初始化；然后再编写 `NewModel.forward` 方法，其定义了模型从接受输入、计算输出这一过程。以 `MLP.__init__` 和 `MLP.forward` 为例，如下所示。 - - === "MLP.\_\_init\_\_" - - ``` py - --8<-- - ppsci/arch/mlp.py:73:138 - --8<-- - ``` - - === "MLP.forward" - - ``` py - --8<-- - ppsci/arch/mlp.py:140:167 - --8<-- - ``` +3. 编写 `__init__` 代码，用于模型创建时的初始化；然后再编写 `forward` 代码，用于定义模型接受输入、 +计算输出这一前向过程。 -4. 在 `ppsci/arch/__init__.py` 中导入编写的新模型类 `NewModel`，并添加到 `__all__` 中 +4. 在 `ppsci/arch/__init__.py` 中导入编写的新模型类，并添加到 `__all__` 中 - ``` py title="ppsci/arch/__init__.py" hl_lines="3 8" + ``` py linenums="1" title="ppsci/arch/__init__.py" hl_lines="3 8" ... ... from ppsci.arch.new_model import NewModel @@ -142,11 +116,8 @@ model = ppsci.arch.MLP(("x", "y"), ("u", "v", "p"), 9, 50, "tanh") ] ``` -完成上述新模型代码编写的工作之后，在 `demo.py` 中，就能通过调用 `ppsci.arch.NewModel`，实例化刚才编写的模型，如下所示。 - -``` py title="examples/demo/demo.py" -model = ppsci.arch.NewModel(...) -``` +完成上述新模型代码编写的工作之后，我们就能像 PaddleScience 内置模型一样，以 +`ppsci.arch.NewModel` 的方式，调用我们编写的新模型类，并用于创建模型实例。 ### 2.4 构建方程 @@ -155,103 +126,39 @@ model = ppsci.arch.NewModel(...) #### 2.4.1 构建已有方程 PaddleScience 内置了一些常见的方程，如 `NavierStokes` 方程，如果您想使用这些内置的方程，可以直接 -调用 [`ppsci.equation.*`](./api/equation.md) 下的 API，并填入方程实例化所需的参数，即可快速构建方程。 +调用 [`ppsci.equation`](./api/equation.md) 下的 API，并填入方程实例化所需的参数，即可快速构建模型。 -``` py title="examples/demo/demo.py" +``` py linenums="1" # create a Vibration equation viv_equation = ppsci.equation.Vibration(2, -4, 0) ``` #### 2.4.2 构建新的方程 -当 PaddleScience 内置的方程无法满足您的需求时，您也可以通过新增方程文件并编写方程代码的方式，使用您自定义的方程。 - -假设需要计算的方程公式如下所示。 - -$$ -\begin{cases} - \begin{align} - \dfrac{\partial u}{\partial x} + \dfrac{\partial u}{\partial y} &= u + 1, \tag{1} \\ - \dfrac{\partial v}{\partial x} + \dfrac{\partial v}{\partial y} &= v. \tag{2} - \end{align} -\end{cases} -$$ - -> 其中 $x$, $y$ 为模型输入，表示$x$、$y$轴坐标；$u=u(x,y)$、$v=v(x,y)$ 是模型输出，表示 $(x,y)$ 处的 $x$、$y$ 轴方向速度。 - -首先我们需要将上述方程进行适当移项，将含有变量、函数的项移动到等式左侧，含有常数的项移动到等式右侧，方便后续转换成程序代码，如下所示。 - -$$ -\begin{cases} - \begin{align} - \dfrac{\partial u}{\partial x} + \dfrac{\partial u}{\partial y} - u &= 1, \tag{3}\\ - \dfrac{\partial v}{\partial x} + \dfrac{\partial v}{\partial y} - v &= 0. \tag{4} - \end{align} -\end{cases} -$$ +当 PaddleScienc 内置的方程无法满足您的需求时，您也可以通过新增方程文件并编写方程代码的方式，使用您自 +定义的方程，步骤如下： -然后就可以将上述移项后的方程组根据以下步骤转换成对应的程序代码。 +1. 在 `ppsci/equation/pde` 下新建方程文件（如果您的方程并不是 PDE 方程，那么需要新建一个方程类文件 +夹，比如在 `ppsci/equation` 下新建 `ode` 文件夹，再将您的方程文件放在 `ode` 文件夹下，此处以 PDE +类的方程 `new_pde.py` 为例） -1. 在 `ppsci/equation/pde/` 下新建方程文件。如果您的方程并不是 PDE 方程，那么需要新建一个方程类文件夹，比如在 `ppsci/equation/` 下新建 `ode` 文件夹，再将您的方程文件放在 `ode` 文件夹下。此处以PDE类的方程 `new_pde.py` 为例。 +2. 在 `new_pde.py` 文件中导入 PaddleScience 的方程基类所在模块 `base`，并让创建的新方程类 +（以`Class NewPDE` 为例）从 `base.PDE` 继承 -2. 在 `new_pde.py` 文件中导入 PaddleScience 的方程基类所在模块 `base`，并从 `base.PDE` 派生 `Class NewPDE`。 - - ``` py title="ppsci/equation/pde/new_pde.py" + ``` py linenums="1" title="ppsci/equation/pde/new_pde.py" from ppsci.equation.pde import base class NewPDE(base.PDE): + def __init__(self, ...): + ... + # init ``` -3. 编写 `__init__` 代码，用于方程创建时的初始化，在其中定义必要的变量和公式计算过程。PaddleScience 支持使用 sympy 符号计算库创建方程和直接使用 python 函数编写方程，两种方式如下所示。 - - === "sympy expression" - - ``` py title="ppsci/equation/pde/new_pde.py" - from ppsci.equation.pde import base - - class NewPDE(base.PDE): - def __init__(self): - x, y = self.create_symbols("x y") # 创建自变量 x, y - u = self.create_function("u", (x, y)) # 创建关于自变量 (x, y) 的函数 u(x,y) - v = self.create_function("v", (x, y)) # 创建关于自变量 (x, y) 的函数 v(x,y) - - expr1 = u.diff(x) + u.diff(y) - u # 对应等式(3)左侧表达式 - expr2 = v.diff(x) + v.diff(y) - v # 对应等式(4)左侧表达式 - - self.add_equation("expr1", expr1) # 将expr1 的 sympy 表达式对象添加到 NewPDE 对象的公式集合中 - self.add_equation("expr2", expr2) # 将expr2 的 sympy 表达式对象添加到 NewPDE 对象的公式集合中 - ``` - - === "python function" - - ``` py title="ppsci/equation/pde/new_pde.py" - from ppsci.autodiff import jacobian - - from ppsci.equation.pde import base - - class NewPDE(base.PDE): - def __init__(self): - def expr1_compute_func(out): - x, y = out["x"], out["y"] # 从 out 数据字典中取出自变量 x, y 的数据值 - u = out["u"] # 从 out 数据字典中取出因变量 u 的函数值 - - expr1 = jacobian(u, x) + jacobian(u, y) - u # 对应等式(3)左侧表达式计算过程 - return expr1 # 返回计算结果值 - - def expr2_compute_func(out): - x, y = out["x"], out["y"] # 从 out 数据字典中取出自变量 x, y 的数据值 - v = out["v"] # 从 out 数据字典中取出因变量 v 的函数值 - - expr2 = jacobian(v, x) + jacobian(v, y) - v # 对应等式(4)左侧表达式计算过程 - return expr2 - - self.add_equation("expr1", expr1_compute_func) # 将 expr1 的计算函数添加到 NewPDE 对象的公式集合中 - self.add_equation("expr2", expr2_compute_func) # 将 expr2 的计算函数添加到 NewPDE 对象的公式集合中 - ``` +3. 编写 `__init__` 代码，用于方程创建时的初始化 4. 在 `ppsci/equation/__init__.py` 中导入编写的新方程类，并添加到 `__all__` 中 - ``` py title="ppsci/equation/__init__.py" hl_lines="3 8" + ``` py linenums="1" title="ppsci/equation/__init__.py" hl_lines="3 8" ... ... from ppsci.equation.pde.new_pde import NewPDE @@ -263,150 +170,29 @@ $$ ] ``` -完成上述新方程代码编写的工作之后，我们就能像 PaddleScience 内置方程一样，以 `ppsci.equation.NewPDE` 的方式，调用我们编写的新方程类，并用于创建方程实例。 +完成上述新方程代码编写的工作之后，我们就能像 PaddleScience 内置方程一样，以 +`ppsci.equation.NewPDE` 的方式，调用我们编写的新方程类，并用于创建方程实例。 在方程构建完毕后之后，我们需要将所有方程包装为到一个字典中 -``` py title="examples/demo/demo.py" +``` py linenums="1" new_pde = ppsci.equation.NewPDE(...) -equation = {..., "newpde": new_pde} -``` - -### 2.5 构建几何模块[可选] - -模型训练、验证时所用的输入、标签数据的来源，根据具体案例场景的不同而变化。大部分基于 PINN 的案例，其数据来自几何形状内部、表面采样得到的坐标点、法向量、SDF 值；而基于数据驱动的方法，其输入、标签数据大多数来自于外部文件，或通过 numpy 等第三方库构造的存放在内存中的数据。本章节主要对第一种情况所需的几何模块进行介绍，第二种情况则不一定需要几何模块，其构造方式可以参考 [#2.6 构建约束条件](#2.6)。 - -#### 2.5.1 构建已有几何 - -PaddleScience 内置了几类常用的几何形状，包括简单几何、复杂几何，如下所示。 - -| 几何调用方式 | 含义 | -| -- | -- | -|`ppsci.geometry.Interval`| 1 维线段几何| -|`ppsci.geometry.Disk`| 2 维圆面几何| -|`ppsci.geometry.Polygon`| 2 维多边形几何| -|`ppsci.geometry.Rectangle` | 2 维矩形几何| -|`ppsci.geometry.Triangle` | 2 维三角形几何| -|`ppsci.geometry.Cuboid` | 3 维立方体几何| -|`ppsci.geometry.Sphere` | 3 维圆球几何| -|`ppsci.geometry.Mesh` | 3 维 Mesh 几何| -|`ppsci.geometry.PointCloud` | 点云几何| -|`ppsci.geometry.TimeDomain` | 1 维时间几何(常用于瞬态问题)| -|`ppsci.geometry.TimeXGeometry` | 1 + N 维带有时间的几何(常用于瞬态问题)| - -以计算域为 2 维矩形几何为例，实例化一个 x 轴边长为2，y 轴边长为 1，且左下角为点 (-1,-3) 的矩形几何代码如下： - -``` py title="examples/demo/demo.py" -LEN_X, LEN_Y = 2, 1 # 定义矩形边长 -rect = ppsci.geometry.Rectangle([-1, -3], [-1 + LEN_X, -3 + LEN_Y]) # 通过左下角、右上角对角线坐标构造矩形 -``` - -其余的几何体构造方法类似，参考 API 文档的 [ppsci.geometry](./api/geometry.md) 部分即可。 - -#### 2.5.2 构建新的几何 - -下面以构建一个新的几何体 —— 2 维椭圆（无旋转）为例进行介绍。 - -1. 首先我们需要在二维几何的代码文件 `ppsci/geometry/geometry_2d.py` 中新建椭圆类 `Ellipse`，并制定其直接父类为 `geometry.Geometry` 几何基类。 -然后根据椭圆的代数表示公式：$\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$，可以发现表示一个椭圆需要记录其圆心坐标 $(x_0,y_0)$、$x$ 轴半径 $a$、$y$ 轴半径 $b$。因此该椭圆类的代码如下所示。 - - ``` py title="ppsci/geometry/geometry_2d.py" - class Ellipse(geometry.Geometry): - def __init__(self, x0: float, y0: float, a: float, b: float) - self.center = np.array((x0, y0), dtype=paddle.get_default_dtype()) - self.a = a - self.b = b - ``` - -2. 为椭圆类编写必要的基础方法，如下所示。 - - - 判断给定点集是否在椭圆内部 - - ``` py title="ppsci/geometry/geometry_2d.py" - def is_inside(self, x): - return ((x / self.center) ** 2).sum(axis=1) < 1 - ``` - - - 判断给定点集是否在椭圆边界上 - - ``` py title="ppsci/geometry/geometry_2d.py" - def on_boundary(self, x): - return np.isclose(((x / self.center) ** 2).sum(axis=1), 1) - ``` - - - 在椭圆内部点随机采样(此处使用“拒绝采样法”实现) - - ``` py title="ppsci/geometry/geometry_2d.py" - def random_points(self, n, random="pseudo"): - res_n = n - result = [] - max_radius = self.center.max() - while (res_n < n): - rng = sampler.sample(n, 2, random) - r, theta = rng[:, 0], 2 * np.pi * rng[:, 1] - x = np.sqrt(r) * np.cos(theta) - y = np.sqrt(r) * np.sin(theta) - candidate = max_radius * np.stack((x, y), axis=1) + self.center - candidate = candidate[self.is_inside(candidate)] - if len(candidate) > res_n: - candidate = candidate[: res_n] - - result.append(candidate) - res_n -= len(candidate) - result = np.concatenate(result, axis=0) - return result - ``` - - - 在椭圆边界随机采样(此处基于椭圆参数方程实现) - - ``` py title="ppsci/geometry/geometry_2d.py" - def random_boundary_points(self, n, random="pseudo"): - theta = 2 * np.pi * sampler.sample(n, 1, random) - X = np.concatenate((self.a * np.cos(theta),self.b * np.sin(theta)), axis=1) - return X + self.center - ``` - -3. 在 `ppsci/geometry/__init__.py` 中加入椭圆类 `Ellipse`，如下所示。 - - ``` py title="ppsci/geometry/__init__.py" hl_lines="3 8" - ... - ... - from ppsci.geometry.geometry_2d import Ellipse - - __all__ = [ - ..., - ..., - "Ellipse", - ] - ``` - -完成上述实现之后，我们就能以如下方式实例化椭圆类。同样地，建议将所有几何类实例包装在一个字典中，方便后续索引。 - -``` py title="examples/demo/demo.py" -ellipse = ppsci.geometry.Ellipse(0, 0, 2, 1) -geom = {..., "ellipse": ellipse} +equation = {"newpde": new_pde} ``` -### 2.6 构建约束条件 - -无论是 PINNs 方法还是数据驱动方法，它们总是需要利用数据来指导网络模型的训练，而这一过程在 PaddleScience 中由 `Constraint`（约束）模块负责。 +### 2.5 构建约束条件 -#### 2.6.1 构建已有约束 +无论是 PINNs 方法还是数据驱动方法，它们总是需要构造数据来指导网络模型的训练，而利用数据指导网络训练的 +这一过程，在 PaddleScience 中由 `Constraint`（约束） 负责。 -PaddleScience 内置了一些常见的约束，如下所示。 +#### 2.5.1 构建已有约束 -|约束名称|功能| -|--|--| -|`ppsci.constraint.BoundaryConstraint`|边界约束| -|`ppsci.constraint.InitialConstraint` |内部点初值约束| -|`ppsci.constraint.IntegralConstraint` |边界积分约束| -|`ppsci.constraint.InteriorConstraint`|内部点约束| -|`ppsci.constraint.PeriodicConstraint` |边界周期约束| -|`ppsci.constraint.SupervisedConstraint` |监督数据约束| +PaddleScience 内置了一些常见的约束，如主要用于数据驱动模型的 `SupervisedConstraint` 监督约束， +主要用于物理信息驱动的 `InteriorConstraint` 内部点约束，如果您想使用这些内置的约束，可以直接调用 +[`ppsci.constraint`](./api/constraint.md) 下的 API，并填入约束实例化所需的参数，即可快速构建约 +束条件。 -如果您想使用这些内置的约束，可以直接调用 [`ppsci.constraint.*`](./api/constraint.md) 下的 API，并填入约束实例化所需的参数，即可快速构建约束条件。 - -``` py title="examples/demo/demo.py" +``` py linenums="1" # create a SupervisedConstraint sup_constraint = ppsci.constraint.SupervisedConstraint( train_dataloader_cfg, @@ -416,11 +202,9 @@ sup_constraint = ppsci.constraint.SupervisedConstraint( ) ``` -约束的参数填写方式，请参考对应的 API 文档参数说明和样例代码。 - -#### 2.6.2 构建新的约束 +#### 2.5.2 构建新的约束 -当 PaddleScience 内置的约束无法满足您的需求时，您也可以通过新增约束文件并编写约束代码的方式，使用您自 +当 PaddleScienc 内置的约束无法满足您的需求时，您也可以通过新增约束文件并编写约束代码的方式，使用您自 定义的约束，步骤如下： 1. 在 `ppsci/constraint` 下新建约束文件（此处以约束 `new_constraint.py` 为例） @@ -428,26 +212,20 @@ sup_constraint = ppsci.constraint.SupervisedConstraint( 2. 在 `new_constraint.py` 文件中导入 PaddleScience 的约束基类所在模块 `base`，并让创建的新约束 类（以 `Class NewConstraint` 为例）从 `base.PDE` 继承 - ``` py title="ppsci/constraint/new_constraint.py" - from ppsci.constraint import base - - class NewConstraint(base.Constraint): - ``` - -3. 编写 `__init__` 方法，用于约束创建时的初始化。 - - ``` py title="ppsci/constraint/new_constraint.py" + ``` py linenums="1" title="ppsci/constraint/new_constraint.py" from ppsci.constraint import base class NewConstraint(base.Constraint): def __init__(self, ...): ... - # initialization + # init ``` +3. 编写 `__init__` 代码，用于约束创建时的初始化 + 4. 在 `ppsci/constraint/__init__.py` 中导入编写的新约束类，并添加到 `__all__` 中 - ``` py title="ppsci/constraint/__init__.py" hl_lines="3 8" + ``` py linenums="1" title="ppsci/constraint/__init__.py" hl_lines="3 8" ... ... from ppsci.constraint.new_constraint import NewConstraint @@ -459,47 +237,38 @@ sup_constraint = ppsci.constraint.SupervisedConstraint( ] ``` -完成上述新约束代码编写的工作之后，我们就能像 PaddleScience 内置约束一样，以 `ppsci.constraint.NewConstraint` 的方式，调用我们编写的新约束类，并用于创建约束实例。 +完成上述新约束代码编写的工作之后，我们就能像 PaddleScience 内置约束一样，以 +`ppsci.constraint.NewConstraint` 的方式，调用我们编写的新约束类，并用于创建约束实例。 -``` py title="examples/demo/demo.py" -new_constraint = ppsci.constraint.NewConstraint(...) -constraint = {..., new_constraint.name: new_constraint} -``` +### 2.6 定义超参数 -### 2.7 定义超参数 +在模型开始训练前，需要定义一些训练相关的超参数，如训练轮数、学习率等，如下所示 -在模型开始训练前，需要定义一些训练相关的超参数，如训练轮数、学习率等，如下所示。 - -``` py title="examples/demo/demo.py" -EPOCHS = 10000 -LEARNING_RATE = 0.001 +``` py linenums="1" +epochs = 10000 +learning_rate = 0.001 ``` -### 2.8 构建优化器 +### 2.7 构建优化器 -模型训练时除了模型本身，还需要定义一个用于更新模型参数的优化器，如下所示。 +模型训练时除了模型本身，还需要定义一个用于更新模型参数的优化器，如下所示 -``` py title="examples/demo/demo.py" +``` py linenums="1" optimizer = ppsci.optimizer.Adam(0.001)(model) ``` -### 2.9 构建评估器[可选] - -#### 2.9.1 构建已有评估器 - -PaddleScience 内置了一些常见的评估器，如下所示。 +### 2.8 构建评估器 -|评估器名称|功能| -|--|--| -|`ppsci.validator.GeometryValidator`|几何评估器| -|`ppsci.validator.SupervisedValidator` |监督数据评估器| +#### 2.8.1 构建已有评估器 -如果您想使用这些内置的评估器，可以直接调用 [`ppsci.validate.*`](./api/validate.md) 下的 API，并填入评估器实例化所需的参数，即可快速构建评估器。 +PaddleScience 内置了一些常见的评估器，如 `SupervisedValidator` 评估器，如果您想使用这些内置的评 +估器，可以直接调用 [`ppsci.validate`](./api/validate.md) 下的 API，并填入评估器实例化所需的参数， +即可快速构建评估器。 -``` py title="examples/demo/demo.py" +``` py linenums="1" # create a SupervisedValidator eta_mse_validator = ppsci.validate.SupervisedValidator( - valid_dataloader_cfg, + valida_dataloader_cfg, ppsci.loss.MSELoss("mean"), {"eta": lambda out: out["eta"], **equation["VIV"].equations}, metric={"MSE": ppsci.metric.MSE()}, @@ -507,35 +276,30 @@ eta_mse_validator = ppsci.validate.SupervisedValidator( ) ``` -#### 2.9.2 构建新的评估器 +#### 2.8.2 构建新的评估器 -当 PaddleScience 内置的评估器无法满足您的需求时，您也可以通过新增评估器文件并编写评估器代码的方式，使 +当 PaddleScienc 内置的评估器无法满足您的需求时，您也可以通过新增评估器文件并编写评估器代码的方式，使 用您自定义的评估器，步骤如下： -1. 在 `ppsci/validate` 下新建评估器文件（此处以 `new_validator.py` 为例）。 +1. 在 `ppsci/validate` 下新建评估器文件（此处以 `new_validator.py` 为例） -2. 在 `new_validator.py` 文件中导入 PaddleScience 的评估器基类所在模块 `base`，并让创建的新评估器类（以 `Class NewValidator` 为例）从 `base.Validator` 继承。 +2. 在 `new_validator.py` 文件中导入 PaddleScience 的评估器基类所在模块 `base`，并让创建的新评估 +器类（以 `Class NewValidator` 为例）从 `base.Validator` 继承 - ``` py title="ppsci/validate/new_validator.py" - from ppsci.validate import base - - class NewValidator(base.Validator): - ``` - -3. 编写 `__init__` 代码，用于评估器创建时的初始化 - - ``` py title="ppsci/validate/new_validator.py" + ``` py linenums="1" title="ppsci/validate/new_validator.py" from ppsci.validate import base class NewValidator(base.Validator): def __init__(self, ...): ... - # initialization + # init ``` -4. 在 `ppsci/validate/__init__.py` 中导入编写的新评估器类，并添加到 `__all__` 中。 +3. 编写 `__init__` 代码，用于评估器创建时的初始化 + +4. 在 `ppsci/validate/__init__.py` 中导入编写的新评估器类，并添加到 `__all__` 中 - ``` py title="ppsci/validate/__init__.py" hl_lines="3 8" + ``` py linenums="1" title="ppsci/validate/__init__.py" hl_lines="3 8" ... ... from ppsci.validate.new_validator import NewValidator @@ -547,20 +311,23 @@ eta_mse_validator = ppsci.validate.SupervisedValidator( ] ``` -完成上述新评估器代码编写的工作之后，我们就能像 PaddleScience 内置评估器一样，以 `ppsci.validate.NewValidator` 的方式，调用我们编写的新评估器类，并用于创建评估器实例。同样地，在评估器构建完毕后之后，建议将所有评估器包装到一个字典中方便后续索引。 +完成上述新评估器代码编写的工作之后，我们就能像 PaddleScience 内置评估器一样，以 +`ppsci.equation.NewValidator` 的方式，调用我们编写的新评估器类，并用于创建评估器实例。 + +在评估器构建完毕后之后，我们需要将所有评估器包装为到一个字典中 -``` py title="examples/demo/demo.py" +``` py linenums="1" new_validator = ppsci.validate.NewValidator(...) -validator = {..., new_validator.name: new_validator} +validator = {new_validator.name: new_validator} ``` -### 2.10 构建可视化器[可选] +### 2.9 构建可视化器 PaddleScience 内置了一些常见的可视化器，如 `VisualizerVtu` 可视化器等，如果您想使用这些内置的可视 -化器，可以直接调用 [`ppsci.visualizer.*`](./api/visualize.md) 下的 API，并填入可视化器实例化所需的 +化器，可以直接调用 [`ppsci.visulizer`](./api/visualize.md) 下的 API，并填入可视化器实例化所需的 参数，即可快速构建模型。 -``` py title="examples/demo/demo.py" +``` py linenums="1" # manually collate input data for visualization, # interior+boundary vis_points = {} @@ -570,7 +337,7 @@ for key in vis_interior_points: ) visualizer = { - "visualize_u_v": ppsci.visualize.VisualizerVtu( + "visulzie_u_v": ppsci.visualize.VisualizerVtu( vis_points, {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, prefix="result_u_v", @@ -580,11 +347,12 @@ visualizer = { 如需新增可视化器，步骤与其他模块的新增方法类似，此处不再赘述。 -### 2.11 构建Solver +### 2.10 构建Solver -[`Solver`](./api/solver.md) 是 PaddleScience 负责调用训练、评估、可视化的全局管理类。在训练开始前，需要把构建好的模型、约束、优化器等实例传给 `Solver` 以实例化，再调用它的内置方法进行训练、评估、可视化。 +[`Solver`](./api/solver.md) 是 PaddleScience 负责调用训练、评估、可视化的类，在训练开始前，需要把构建好的模型、约束、优化 +器等实例传给 Solver，再调用它的内置方法进行训练、评估、可视化。 -``` py title="examples/demo/demo.py" +``` py linenums="1" # initialize solver solver = ppsci.solver.Solver( model, @@ -592,7 +360,7 @@ solver = ppsci.solver.Solver( output_dir, optimizer, lr_scheduler, - EPOCHS, + epochs, iters_per_epoch, eval_during_train=True, eval_freq=eval_freq, @@ -602,85 +370,39 @@ solver = ppsci.solver.Solver( ) ``` -### 2.12 训练 +### 2.11 训练 -PaddleScience 模型的训练只需调用一行代码。 +PaddleScience 模型的训练只需调用一行代码 -``` py title="examples/demo/demo.py" +``` py linenums="1" solver.train() ``` -### 2.13 评估 +### 2.12 评估 -PaddleScience 模型的评估只需调用一行代码。 +PaddleScience 模型的评估只需调用一行代码 -``` py title="examples/demo/demo.py" +``` py linenums="1" solver.eval() ``` -### 2.14 可视化[可选] +### 2.13 可视化 -若 `Solver` 实例化时传入了 `visualizer` 参数，则 PaddleScience 模型的可视化只需调用一行代码。 +PaddleScience 模型的可视化只需调用一行代码 -``` py title="examples/demo/demo.py" +``` py linenums="1" solver.visualize() ``` -!!! tip "可视化方案" - - 对于一些复杂的案例，`Visualizer` 的编写成本并不低，并且不是任何数据类型都可以进行方便的可视化。因此可以在训练完成之后，手动构建用于预测的数据字典，再使用 `solver.predict` 得到模型预测结果，最后利用 `matplotlib` 等第三方库，对预测结果进行可视化并保存。 - -## 3. 编写文档 - -除了案例代码，PaddleScience 同时存放了对应案例的详细文档，使用 Markdown + [Mkdocs-Material](https://squidfunk.github.io/mkdocs-material/) 进行编写和渲染，撰写文档步骤如下。 - -### 3.1 安装必要依赖包 - -文档撰写过程中需进行即时渲染，预览文档内容以检查撰写的内容是否有误。因此需要按照如下命令，安装 mkdocs 相关依赖包。 - -``` shell -pip install -r docs/requirements.txt -i https://pypi.tuna.tsinghua.edu.cn/simple -``` - -### 3.2 撰写文档内容 - -PaddleScience 文档基于 [Mkdocs-Material](https://squidfunk.github.io/mkdocs-material/)、[PyMdown](https://facelessuser.github.io/pymdown-extensions/extensions/arithmatex/) 等插件进行编写，其在 Markdown 语法基础上支持了多种扩展性功能，能极大地提升文档的美观程度和阅读体验。建议参考超链接内的文档内容，选择合适的功能辅助文档撰写。 - -### 3.3 预览文档 - -在 `PaddleScience/` 目录下执行以下命令，等待构建完成后，点击显示的链接进入本地网页预览文档内容。 - -``` shell -mkdocs serve - -# ====== 终端打印信息如下 ====== -# INFO - Building documentation... -# INFO - Cleaning site directory -# INFO - Documentation built in 20.95 seconds -# INFO - [07:39:35] Watching paths for changes: 'docs', 'mkdocs.yml' -# INFO - [07:39:35] Serving on http://127.0.0.1:8000/PaddlePaddle/PaddleScience/ -# INFO - [07:39:41] Browser connected: http://127.0.0.1:58903/PaddlePaddle/PaddleScience/ -# INFO - [07:40:41] Browser connected: http://127.0.0.1:58903/PaddlePaddle/PaddleScience/zh/development/ -``` - -!!! tip "手动指定服务地址和端口号" - - 若默认端口号 8000 被占用，则可以手动指定服务部署的地址和端口，示例如下。 - - ``` shell - # 指定 127.0.0.1 为地址，8687 为端口号 - mkdocs serve -a 127.0.0.1:8687 - ``` - -## 4. 整理代码并提交 +## 3. 整理代码并提交 -### 4.1 安装 pre-commit +### 3.1 安装 pre-commit PaddleScience 是一个开源的代码库，由多人共同参与开发，因此为了保持最终合入的代码风格整洁、一致， PaddleScience 使用了包括 [isort](https://github.com/PyCQA/isort#installing-isort)、[black](https://github.com/psf/black) 等自动化代码检查、格式化插件， 让 commit 的代码遵循 python [PEP8](https://pep8.org/) 代码风格规范。 -因此在 commit 您的代码之前，请务必先执行以下命令安装 `pre-commit`。 +因此在 commit 你的代码之前，请务必先执行以下命令安装 `pre-commit`。 ``` sh pip install pre-commit @@ -689,12 +411,12 @@ pre-commit install 关于 pre-commit 的详情请参考 [Paddle 代码风格检查指南](https://www.paddlepaddle.org.cn/documentation/docs/zh/develop/dev_guides/git_guides/codestyle_check_guide_cn.html) -### 4.2 整理代码 +### 3.2 整理代码 在完成范例编写与训练后，确认结果无误，就可以整理代码。 使用 git 命令将所有新增、修改的代码文件以及必要的文档、图片等一并上传到自己仓库的 `dev_model` 分支上。 -### 4.3 提交 pull request +### 3.3 提交 pull request 在 github 网页端切换到 `dev_model` 分支，并点击 "Contribute"，再点击 "Open pull request" 按钮， -将含有您的代码、文档、图片等内容的 `dev_model` 分支作为合入请求贡献到 PaddleScience。 +将含有你的代码、文档、图片等内容的 `dev_model` 分支作为合入请求贡献到 PaddleScience。 diff --git a/docs/zh/examples/NSFNet.md b/docs/zh/examples/NSFNet.md new file mode 100644 index 000000000..2ba347562 --- /dev/null +++ b/docs/zh/examples/NSFNet.md @@ -0,0 +1,184 @@ +# NSFNet + +AI Studio快速体验 + +=== "模型训练命令" + + ``` sh + # VP_NSFNet1 + python VP_NSFNet1.py + + # VP_NSFNet2 + python VP_NSFNet2.py + + # VP_NSFNet3 + python VP_NSFNet3.py + ``` + +## 1. 背景简介 + 最近几年，深度学习在很多领域取得了非凡的成就，尤其是计算机视觉和自然语言处理方面，而受启发于深度学习的快速发展，基于深度学习强大的函数逼近能力，神经网络在科学计算领域也取得了成功，现阶段的研究主要分为两大类，一类是将物理信息以及物理限制加入损失函数来对神经网络进行训练, 其代表有 PINN 以及 Deep Retz Net，另一类是通过数据驱动的深度神经网络算子，其代表有 FNO 以及 DeepONet。这些方法都在科学实践中获得了广泛应用，比如天气预测，量子化学，生物工程，以及计算流体等领域。而为充分探索PINN对流体方程的求解能力，本次复现[论文](https://arxiv.org/abs/2003.06496)作者先后使用具有解析解或数值解的二维、三维纳韦斯托克方程以及使用DNS方法进行高进度求解的数据集进行训练。论文实验表明PINN对不可压纳韦斯托克方程具有优秀的数值求解能力，本项目主要目标是使用PaddleScience复现论文所实现的高精度求解纳韦斯托克方程的代码。 +## 2. 问题定义 +本问题所使用的为最经典的PINN模型，对此不再赘述。 + +主要介绍所求解的几类纳韦斯托克方程： + +不可压纳韦斯托克方程可以表示为： +$$\frac{\partial \mathbf{u}}{\partial t}+(\mathbf{u} \cdot \nabla) \mathbf{u} =-\nabla p+\frac{1}{Re} \nabla^2 \mathbf{u} \quad \text { in } \Omega,$$ + +$$\nabla \cdot \mathbf{u} =0 \quad \text { in } \Omega,$$ + +$$\mathbf{u} =\mathbf{u}_{\Gamma} \quad \text { on } \Gamma_D,$$ + +$$\frac{\partial \mathbf{u}}{\partial n} =0 \quad \text { on } \Gamma_N.$$ + +### 2.1 Kovasznay flow +$$u(x, y)=1-e^{\lambda x} \cos (2 \pi y),$$ + +$$v(x, y)=\frac{\lambda}{2 \pi} e^{\lambda x} \sin (2 \pi y),$$ + +$$p(x, y)=\frac{1}{2}\left(1-e^{2 \lambda x}\right),$$ + +其中 +$$\lambda=\frac{1}{2 \nu}-\sqrt{\frac{1}{4 \nu^2}+4 \pi^2}, \quad \nu=\frac{1}{Re}=\frac{1}{40} .$$ +### 2.2 Cylinder wake +该方程并没有解析解，为雷诺数为100的数值解，[AIstudio数据集](https://aistudio.baidu.com/datasetdetail/236213)。 +### 2.3 Beltrami flow +$$u(x, y, z, t)= -a\left[e^{a x} \sin (a y+d z)+e^{a z} \cos (a x+d y)\right] e^{-d^2 t}, $$ + +$$v(x, y, z, t)= -a\left[e^{a y} \sin (a z+d x)+e^{a x} \cos (a y+d z)\right] e^{-d^2 t}, $$ + +$$w(x, y, z, t)= -a\left[e^{a z} \sin (a x+d y)+e^{a y} \cos (a z+d x)\right] e^{-d^2 t}, $$ + +$$p(x, y, z, t)= -\frac{1}{2} a^2\left[e^{2 a x}+e^{2 a y}+e^{2 a z}+2 \sin (a x+d y) \cos (a z+d x) e^{a(y+z)} +2 \sin (a y+d z) \cos (a x+d y) e^{a(z+x)} +2 \sin (a z+d x) \cos (a y+d z) e^{a(x+y)}\right] e^{-2 d^2 t}.$$ +## 3. 问题求解 +为节约篇幅，问题求解以NSFNet3为例。 +### 3.1 模型构建 +本文使用PINN经典的MLP模型进行训练。 +``` py linenums="33" +--8<-- +examples/NSFNet/VP_NSFNet3.py:175:175 +--8<-- +``` +### 3.2 超参数设定 +指定残差点、边界点、初值点的个数，以及可以指定边界损失函数和初值损失函数的权重 +``` py linenums="41" +--8<-- +examples/NSFNet/VP_NSFNet3.py:178:186 +--8<-- +``` +### 3.3 数据生成 +因数据集为解析解，我们先构造解析解函数 +``` py linenums="10" +--8<-- +examples/NSFNet/VP_NSFNet3.py:10:51 +--8<-- +``` + +然后先后取边界点、初值点、以及用于计算残差的内部点（具体取法见[论文](https://arxiv.org/abs/2003.06496)节3.3）以及生成测试点。 +``` py linenums="53" +--8<-- +examples/NSFNet/VP_NSFNet3.py:187:214 +--8<-- +``` +### 3.4 约束构建 +由于我们边界点和初值点具有解析解，因此我们使用监督约束 +``` py linenums="173" +--8<-- +examples/NSFNet/VP_NSFNet3.py:266:277 +--8<-- +``` + +其中alpha和beta为该损失函数的权重，在本代码中与论文中描述一致，都取为100 + +使用内部点构造纳韦斯托克方程的残差约束 +``` py linenums="188" +--8<-- +examples/NSFNet/VP_NSFNet3.py:280:297 +--8<-- +``` +### 3.5 评估器构建 +使用在数据生成时生成的测试点构造的测试集用于模型评估： +``` py linenums="208" +--8<-- +examples/NSFNet/VP_NSFNet3.py:305:313 +--8<-- +``` + +### 3.6 优化器构建 +与论文中描述相同，我们使用分段学习率构造Adam优化器，其中可以通过调节_epoch_list_来调节训练轮数。 +``` py linenums="219" +--8<-- +examples/NSFNet/VP_NSFNet3.py:316:325 +--8<-- +``` + +### 3.7 模型训练与评估 +完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`。 + +``` py linenums="230" +--8<-- +examples/NSFNet/VP_NSFNet3.py:328:345 +--8<-- +``` + +最后启动训练即可： + +``` py linenums="249" +--8<-- +examples/NSFNet/VP_NSFNet3.py:350:350 +--8<-- +``` + + +## 4. 完整代码 +``` py linenums="1" title="NSFNet.py" +--8<-- +examples/NSFNet/VP_NSFNet1.py +examples/NSFNet/VP_NSFNet2.py +examples/NSFNet/VP_NSFNet3.py +--8<-- +``` +## 5. 结果展示 +### NSFNet1: +| size 4*50 | paper | code(without BFGS) | PaddleScience | +|-------------------|--------|--------------------|---------| +| u | 0.084% | 0.062% | 0.055% | +| v | 0.425% | 0.431% | 0.399% | +### NSFNet2: +T=0 +| size 10*100| paper | code(without BFGS) | PaddleScience | +|-------------------|--------|--------------------|---------| +| u | /| 0.403% | 0.138% | +| v | / | 1.5% | 0.488% | + +速度场 + +![image](https://github.com/DUCH714/hackthon5th53/blob/develop/examples/NSFNet/fig/Cylinder%20wake.gif) + +涡流场（t=4.0） + +![image](https://github.com/DUCH714/hackthon5th53/blob/develop/examples/NSFNet/fig/NSFNet2_vorticity.png) +### NSFNet3: +Test dataset: +| size 10*100 | code(without BFGS) | PaddleScience | +|-------------------|--------------------|---------| +| u | 0.0766% | 0.059% | +| v | 0.0689% | 0.082% | +| w | 0.109% | 0.0732% | + +T=1 +| size 10*100 | paper | PaddleScience | +|-------------------|--------|---------| +| u | 0.426% | 0.115% | +| v | 0.366% | 0.199% | +| w | 0.587% | 0.217% | + +速度场 z=0 +![image](https://github.com/DUCH714/hackthon5th53/blob/develop/examples/NSFNet/fig/Beltrami%20flow.gif) + +## 6. 结果说明 +我们使用PINN对不可压纳韦斯托克方程进行数值求解。在PINN中，随机选取的时间和空间的坐标被当作输入值，所对应的速度场以及压强场被当作输出值，使用初值、边界条件当作监督约束以及纳韦斯托克方程本身的当作无监督约束条件加入损失函数进行训练。我们针对三个不同类型的PINN纳韦斯托克方程，设计了三个不同结构神经网络，即NSFNet1、NSFNet2、NSFNet3。通过损失函数的下降可以证明神经网络在求解纳韦斯托克方程中的收敛性，表明PINN拥有对不可压纳韦斯托克方程的求解能力。而通过实验结果表明，三个NSFNet方程都可以很好的逼近对应的纳韦斯托克方程，并且，我们发现增加边界约束以及初值约束的权重可以使得神经网络拥有更好的逼近效果。 +## 7. 参考资料 +[NSFnets (Navier-Stokes Flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations](https://arxiv.org/abs/2003.06496) + +[Github NSFnets](https://github.com/Alexzihaohu/NSFnets/tree/master) diff --git a/docs/zh/examples/bracket.md b/docs/zh/examples/bracket.md index b42ea7a34..747e1aaf9 100644 --- a/docs/zh/examples/bracket.md +++ b/docs/zh/examples/bracket.md @@ -2,34 +2,6 @@ -=== "模型训练命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/bracket/bracket_dataset.tar - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/bracket/bracket_dataset.tar --output bracket_dataset.tar - # unzip it - tar -xvf bracket_dataset.tar - python bracket.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/bracket/bracket_dataset.tar - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/bracket/bracket_dataset.tar --output bracket_dataset.tar - # unzip it - tar -xvf bracket_dataset.tar - python bracket.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/bracket/bracket_pretrained.pdparams - ``` - -| 预训练模型 | 指标 | -|:--| :--| -| [bracket_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/bracket/bracket_pretrained.pdparams) | loss(commercial_ref_u_v_w_sigmas): 32.28704
MSE.u(commercial_ref_u_v_w_sigmas): 0.00005
MSE.v(commercial_ref_u_v_w_sigmas): 0.00000
MSE.w(commercial_ref_u_v_w_sigmas): 0.00734
MSE.sigma_xx(commercial_ref_u_v_w_sigmas): 27.64751
MSE.sigma_yy(commercial_ref_u_v_w_sigmas): 1.23101
MSE.sigma_zz(commercial_ref_u_v_w_sigmas): 0.89106
MSE.sigma_xy(commercial_ref_u_v_w_sigmas): 0.84370
MSE.sigma_xz(commercial_ref_u_v_w_sigmas): 1.42126
MSE.sigma_yz(commercial_ref_u_v_w_sigmas): 0.24510 | - ## 1. 背景简介 线弹性方程在形变分析中起着核心的作用。在物理和工程领域，形变分析是研究物体在外力作用下的形状和尺寸变化的方法。线弹性方程是描述物体在受力后恢复原状的能力的数学模型。具体来说，线弹性方程通常是指应力和应变之间的关系。应力是一个物理量，用于描述物体内部由于外力而产生的单位面积上的力。应变则描述了物体的形状和尺寸的变化。线弹性方程通常可以表示为应力和应变之间的线性关系，即应力和应变是成比例的。这种关系可以用一个线性方程来表示，其中系数被称为弹性模量（或杨氏模量）。这种模型假设物体在受力后能够完全恢复原状，即没有永久变形。这种假设在许多情况下是合理的，例如在研究金属的力学行为时。然而，对于某些材料（如塑料或橡胶），这种假设可能不准确，因为它们在受力后可能会产生永久变形。线弹性方程只是形变分析中的一部分。要全面理解形变，还需要考虑其他因素，例如物体的初始形状和尺寸、外力的历史、材料的其他物理性质（如热膨胀系数和密度）等。然而，线弹性方程提供了一个基本的框架，用于描述和理解物体在受力后的行为。 @@ -45,9 +17,9 @@ 上述连接件包括一个垂直于 x 轴的背板和与之连接的垂直于 z 轴的带孔平板。其中背板处于固定状态，带孔平板的最右侧表面（红色区域）受到 z 轴负方向，单位面积大小为 $4 \times 10^4 Pa$ 的应力；除此之外，其他参数包括弹性模量 $E=10^{11} Pa$，泊松比 $\nu=0.3$。通过设置特征长度 $L=1m$，特征位移 $U=0.0001m$，无量纲剪切模量 $0.01\mu$，目标求解该金属件表面每个点的 $u$、$v$、$w$、$\sigma_{xx}$、$\sigma_{yy}$、$\sigma_{zz}$、$\sigma_{xy}$、$\sigma_{xz}$、$\sigma_{yz}$ 共 9 个物理量。常量定义代码如下： -``` py linenums="29" +``` py linenums="38" --8<-- -examples/bracket/bracket.py:29:38 +examples/bracket/bracket.py:38:49 --8<-- ``` @@ -73,7 +45,7 @@ $$ ``` py linenums="23" --8<-- -examples/bracket/bracket.py:23:27 +examples/bracket/bracket.py:23:36 --8<-- ``` @@ -96,9 +68,9 @@ $$ \end{cases} $$ -``` py linenums="40" +``` py linenums="51" --8<-- -examples/bracket/bracket.py:40:45 +examples/bracket/bracket.py:51:56 --8<-- ``` @@ -127,9 +99,9 @@ tar -xvf bracket_dataset.tar 然后通过 PaddleScience 内置的 STL 几何类 `Mesh` 来读取、解析这些几何文件，并且通过布尔运算，组合出各个计算域，代码如下： -``` py linenums="47" +``` py linenums="58" --8<-- -examples/bracket/bracket.py:47:59 +examples/bracket/bracket.py:58:71 --8<-- ``` @@ -137,9 +109,9 @@ examples/bracket/bracket.py:47:59 本案例共涉及到 5 个约束，在具体约束构建之前，可以先构建数据读取配置，以便后续构建多个约束时复用该配置。 -``` py linenums="61" +``` py linenums="73" --8<-- -examples/bracket/bracket.py:61:71 +examples/bracket/bracket.py:73:84 --8<-- ``` @@ -147,9 +119,9 @@ examples/bracket/bracket.py:61:71 以作用在背板内部点的 `InteriorConstraint` 为例，代码如下： -``` py linenums="114" +``` py linenums="127" --8<-- -examples/bracket/bracket.py:114:150 +examples/bracket/bracket.py:127:163 --8<-- ``` @@ -171,53 +143,53 @@ examples/bracket/bracket.py:114:150 另一个作用在带孔平板上的约束条件则与之类似，代码如下： -``` py linenums="151" +``` py linenums="164" --8<-- -examples/bracket/bracket.py:151:187 +examples/bracket/bracket.py:164:200 --8<-- ``` #### 3.4.2 边界约束 -对于背板后表面，由于被固定，所以其上的点在三个方向的形变均为 0，因此有如下的边界约束条件： +对于背板后表面，由于被固定，所以其上的点在三个方向的应变均为 0，因此有如下的边界约束条件： -``` py linenums="84" +``` py linenums="97" --8<-- -examples/bracket/bracket.py:84:93 +examples/bracket/bracket.py:97:106 --8<-- ``` -对于带孔平板右侧长方形载荷面，其上的每个点只受 z 正方向的载荷，大小为 $T$，其余方向应力为 0，有如下边界条件约束： +对于带孔平板右侧长方形载荷面，其上的每个点只受 z 正方向的应力，大小为 $T$，其余方向应力为 0，有如下边界条件约束： -``` py linenums="94" +``` py linenums="107" --8<-- -examples/bracket/bracket.py:94:102 +examples/bracket/bracket.py:107:115 --8<-- ``` -对于除背板后面、带孔平板右侧长方形载荷面外的表面，不受任何载荷，即三个方向的内力平衡，合力为 0，有如下边界条件约束： +对于除背板后面、带孔平板右侧长方形载荷面外的表面，不受任何应力，即三个方向的应力为 0，有如下边界条件约束： -``` py linenums="103" +``` py linenums="116" --8<-- -examples/bracket/bracket.py:103:113 +examples/bracket/bracket.py:116:126 --8<-- ``` 在方程约束、边界约束构建完毕之后，以刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="188" +``` py linenums="201" --8<-- -examples/bracket/bracket.py:188:195 +examples/bracket/bracket.py:201:208 --8<-- ``` ### 3.5 超参数设定 -接下来需要在配置文件中指定训练轮数，此处按实验经验，使用 2000 轮训练轮数，每轮进行 1000 步优化。 +接下来需要指定训练轮数和学习率，此处按实验经验，使用 2000 轮训练轮数。 -``` yaml linenums="62" +``` py linenums="210" --8<-- -examples/bracket/conf/bracket.yaml:71:74 +examples/bracket/bracket.py:210:211 --8<-- ``` @@ -225,9 +197,9 @@ examples/bracket/conf/bracket.yaml:71:74 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器，并配合使用机器学习中常用的 ExponentialDecay 学习率调整策略。 -``` py linenums="197" +``` py linenums="213" --8<-- -examples/bracket/bracket.py:197:201 +examples/bracket/bracket.py:213:222 --8<-- ``` @@ -235,17 +207,17 @@ examples/bracket/bracket.py:197:201 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，而验证集的数据来自外部 txt 文件，因此首先使用 `ppsci.utils.reader` 模块从 txt 文件中读取验证点集： -``` py linenums="203" +``` py linenums="224" --8<-- -examples/bracket/bracket.py:203:264 +examples/bracket/bracket.py:224:285 --8<-- ``` 然后将其转换为字典并进行无量纲化和归一化，再将其包装成字典和 `eval_dataloader_cfg`（验证集dataloader配置，构造方式与 `train_dataloader_cfg` 类似）一起传递给 `ppsci.validate.SupervisedValidator` 构造评估器。 -``` py linenums="266" +``` py linenums="287" --8<-- -examples/bracket/bracket.py:266:311 +examples/bracket/bracket.py:287:332 --8<-- ``` @@ -255,9 +227,9 @@ examples/bracket/bracket.py:266:311 本文中的输入数据是评估器构建中准备好的输入字典 `input_dict`，输出数据是对应的 9 个预测的物理量，因此只需要将评估的输出数据保存成 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="313" +``` py linenums="334" --8<-- -examples/bracket/bracket.py:313:330 +examples/bracket/bracket.py:334:351 --8<-- ``` @@ -265,9 +237,9 @@ examples/bracket/bracket.py:313:330 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估、可视化。 -``` py linenums="332" +``` py linenums="353" --8<-- -examples/bracket/bracket.py:332:359 +examples/bracket/bracket.py:353:379 --8<-- ``` @@ -281,21 +253,21 @@ examples/bracket/bracket.py ## 5. 结果展示 -下面展示了在测试点集上，3 个方向的挠度 $u, v, w$ 以及 6 个应力 $\sigma_{xx}, \sigma_{yy}, \sigma_{zz}, \sigma_{xy}, \sigma_{xz}, \sigma_{yz}$ 的模型预测结果、传统算法求解结果以及两者的差值。 +下面展示了在测试点集上，3 个方向的应变 $u, v, w$ 以及 6 个应力 $\sigma_{xx}, \sigma_{yy}, \sigma_{zz}, \sigma_{xy}, \sigma_{xz}, \sigma_{yz}$ 的模型预测结果、传统算法求解结果以及两者的差值。
![bracket_compare.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/Bracket/u.png){ loading=lazy } -
左侧为金属件表面预测的挠度 u；中间表示传统算法求解的挠度 u；右侧表示两者差值
+
左侧为金属件表面预测的应变 u；中间表示传统算法求解的应变 u；右侧表示两者差值
![bracket_compare.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/Bracket/v.png){ loading=lazy } -
左侧为金属件表面预测的挠度 v；中间表示传统算法求解的挠度 v；右侧表示两者差值
+
左侧为金属件表面预测的应变 v；中间表示传统算法求解的应变 v；右侧表示两者差值
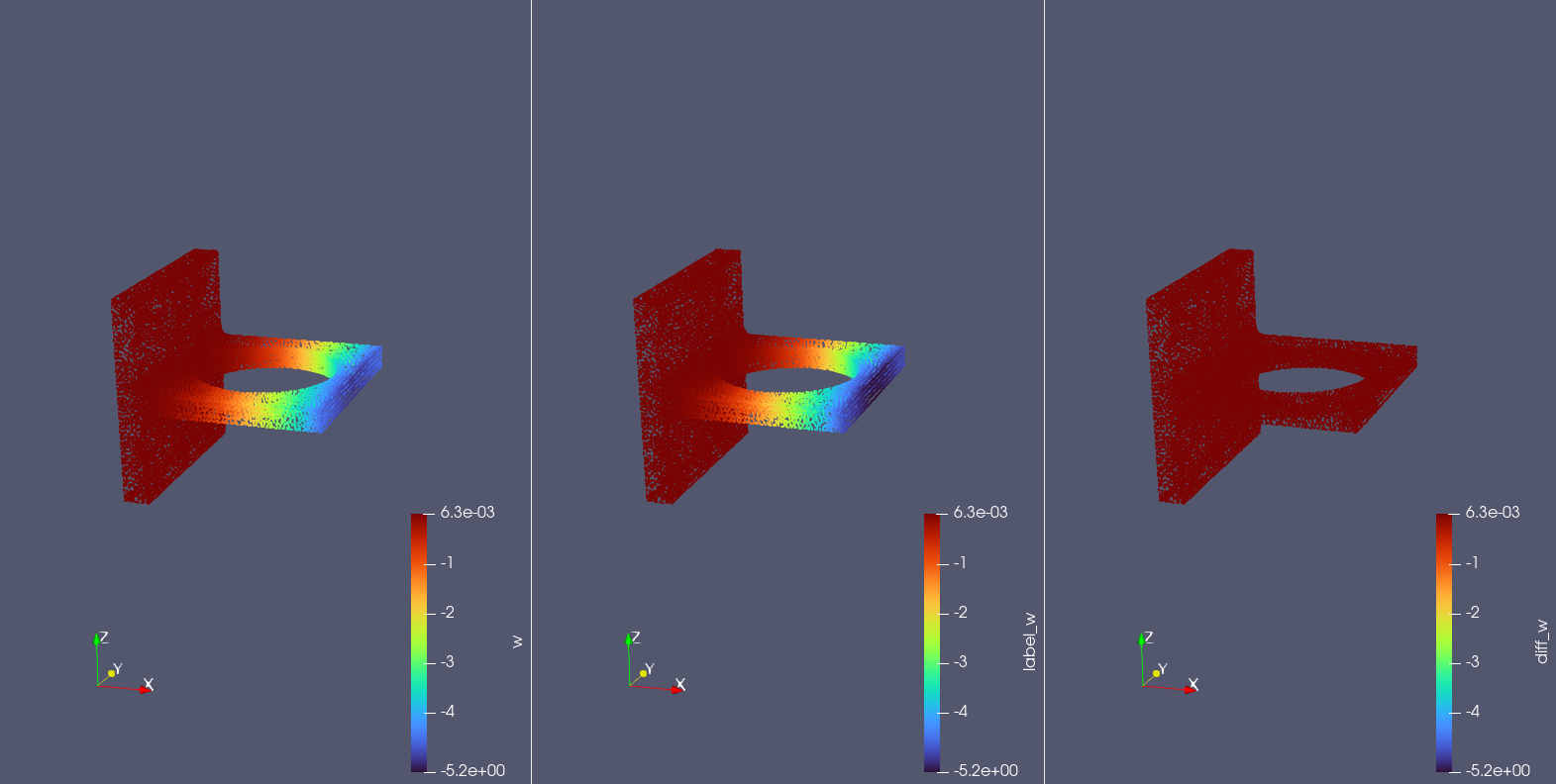![bracket_compare.jpg](https://paddle-org.bj.bcebos.com/paddlescience/docs/Bracket/w.png){ loading=lazy } -
左侧为金属件表面预测的挠度 w；中间表示传统算法求解的挠度 w；右侧表示两者差值
+
左侧为金属件表面预测的应变 w；中间表示传统算法求解的应变 w；右侧表示两者差值
diff --git a/docs/zh/examples/bubble.md b/docs/zh/examples/bubble.md index c6397a860..5587a55a2 100644 --- a/docs/zh/examples/bubble.md +++ b/docs/zh/examples/bubble.md @@ -1,25 +1,5 @@ # Bubble_flow -=== "模型训练命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat --output bubble.mat - python bubble.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat --output bubble.mat - python bubble.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/bubble/bubble_pretrained.pdparams - ``` - ## 1. 背景简介 ### 1.1 气泡流 @@ -131,9 +111,9 @@ $$\mathcal{L}=\frac{1}{m} \sum_{i=1}^m\left(\mathcal{W}_{\text {pred }(i)}-\math 下载后，我们需要首先对数据集进行时间离散归一化（TDN）处理，同时构造训练集和验证集。 -``` py linenums="40" +``` py linenums="39" --8<-- -examples/bubble/bubble.py:40:84 +examples/bubble/bubble.py:39:83 --8<-- ``` @@ -151,25 +131,25 @@ $$ 上式中 $f_1,f_2,f_3$ 均为 MLP 模型，用 PaddleScience 代码表示如下 -``` py linenums="86" +``` py linenums="85" --8<-- -examples/bubble/bubble.py:86:89 +examples/bubble/bubble.py:85:88 --8<-- ``` 使用 `transform_out` 函数实现流函数 $\psi$ 到速度 $u,~v$ 的变换，代码如下 -``` py linenums="91" +``` py linenums="90" --8<-- -examples/bubble/bubble.py:91:98 +examples/bubble/bubble.py:90:97 --8<-- ``` 同时需要对模型 `model_psi` 注册相应的 transform ，然后将 3 个 MLP 模型组成 `Model_List` -``` py linenums="100" +``` py linenums="99" --8<-- -examples/bubble/bubble.py:100:102 +examples/bubble/bubble.py:99:101 --8<-- ``` @@ -181,9 +161,9 @@ examples/bubble/bubble.py:100:102 同时构造可视化区域，即以 [0, 0], [15, 5] 为对角线的二维矩形区域，且时间域为 126 个时刻 [1, 2,..., 125, 126]，该区域可以直接使用 PaddleScience 内置的空间几何 `Rectangle` 和时间域 `TimeDomain`，组合成时间-空间的 `TimeXGeometry` 计算域。代码如下 -``` py linenums="104" +``` py linenums="103" --8<-- -examples/bubble/bubble.py:104:116 +examples/bubble/bubble.py:103:115 --8<-- ``` @@ -203,9 +183,9 @@ examples/bubble/bubble.py:104:116 我们以内部点约束 `InteriorConstraint` 来实现在损失函数中加入压力泊松方程的约束，代码如下： -``` py linenums="121" +``` py linenums="120" --8<-- -examples/bubble/bubble.py:121:136 +examples/bubble/bubble.py:120:136 --8<-- ``` @@ -255,9 +235,9 @@ examples/bubble/bubble.py:156:160 接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用一万轮训练轮数，评估间隔为一千轮，学习率设为 0.001。 -``` yaml linenums="52" +``` py linenums="162" --8<-- -examples/bubble/conf/bubble.yaml:52:56 +examples/bubble/bubble.py:162:164 --8<-- ``` @@ -265,9 +245,9 @@ examples/bubble/conf/bubble.yaml:52:56 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 -``` py linenums="162" +``` py linenums="165" --8<-- -examples/bubble/bubble.py:162:163 +examples/bubble/bubble.py:165:166 --8<-- ``` @@ -275,9 +255,9 @@ examples/bubble/bubble.py:162:163 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.SupervisedValidator` 构建评估器。 -``` py linenums="165" +``` py linenums="168" --8<-- -examples/bubble/bubble.py:165:186 +examples/bubble/bubble.py:168:189 --8<-- ``` @@ -287,9 +267,9 @@ examples/bubble/bubble.py:165:186 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。 -``` py linenums="189" +``` py linenums="191" --8<-- -examples/bubble/bubble.py:189:206 +examples/bubble/bubble.py:191:219 --8<-- ``` @@ -297,9 +277,9 @@ examples/bubble/bubble.py:189:206 最后在给定的可视化区域上进行预测并可视化，可视化数据是区域内的二维点集，每个时刻 $t$ 的坐标是 $(x^t_i, y^t_i)$，对应值是 $(u^t_i, v^t_i, p^t_i,\phi^t_i)$，在此我们对预测得到的 $(u^t_i, v^t_i, p^t_i,\phi^t_i)$ 进行反归一化，我们将反归一化后的数据按时刻保存成 126 个 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="212" +``` py linenums="225" --8<-- -examples/bubble/bubble.py:212:237 +examples/bubble/bubble.py:221:251 --8<-- ``` diff --git a/docs/zh/examples/cylinder2d_unsteady.md b/docs/zh/examples/cylinder2d_unsteady.md index 653532994..9c76d360b 100644 --- a/docs/zh/examples/cylinder2d_unsteady.md +++ b/docs/zh/examples/cylinder2d_unsteady.md @@ -95,13 +95,6 @@ $$ 接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。 为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 [API文档](../api/arch.md)。 -在开始构建代码之前，请先按照下列命令下载训练、评估所需的数据集 - -``` sh -wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/cylinder2d_unsteady_Re100/cylinder2d_unsteady_Re100_dataset.tar -tar -xf cylinder2d_unsteady_Re100_dataset.tar -``` - ### 3.1 模型构建 在 2D-Cylinder 问题中，每一个已知的坐标点 $(t, x, y)$ 都有自身的横向速度 $u$、纵向速度 $v$、压力 $p$ diff --git a/docs/zh/examples/darcy2d.md b/docs/zh/examples/darcy2d.md index 681a1e669..065e881dd 100644 --- a/docs/zh/examples/darcy2d.md +++ b/docs/zh/examples/darcy2d.md @@ -2,18 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - python darcy2d.py - ``` - -=== "模型评估命令" - - ``` sh - python darcy2d.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/darcy2d/darcy2d_pretrained.pdparams - ``` - ## 1. 背景简介 Darcy Flow是一个基于达西定律的工具，用于计算液体的流动。在地下水模拟、水文学、水文地质学和石油工程等领域中，Darcy Flow被广泛应用。 @@ -54,9 +42,9 @@ $$ 上式中 $f$ 即为 MLP 模型本身，用 PaddleScience 代码表示如下 -``` py linenums="33" +``` py linenums="32" --8<-- -examples/darcy/darcy2d.py:33:34 +examples/darcy/darcy2d.py:32:33 --8<-- ``` @@ -68,9 +56,9 @@ examples/darcy/darcy2d.py:33:34 由于 2D-Poisson 使用的是 Poisson 方程的2维形式，因此可以直接使用 PaddleScience 内置的 `Poisson`，指定该类的参数 `dim` 为2。 -``` py linenums="36" +``` py linenums="35" --8<-- -examples/darcy/darcy2d.py:36:37 +examples/darcy/darcy2d.py:35:36 --8<-- ``` @@ -79,9 +67,9 @@ examples/darcy/darcy2d.py:36:37 本文中 2D darcy 问题作用在以 (0.0, 0.0), (1.0, 1.0) 为对角线的二维矩形区域， 因此可以直接使用 PaddleScience 内置的空间几何 `Rectangle` 作为计算域。 -``` py linenums="39" +``` py linenums="38" --8<-- -examples/darcy/darcy2d.py:39:40 +examples/darcy/darcy2d.py:38:39 --8<-- ``` @@ -91,9 +79,9 @@ examples/darcy/darcy2d.py:39:40 在定义约束之前，需要给每一种约束指定采样点个数，表示每一种约束在其对应计算域内采样数据的数量，以及通用的采样配置。 -``` py linenums="42" +``` py linenums="41" --8<-- -examples/darcy/darcy2d.py:42:46 +examples/darcy/darcy2d.py:41:49 --8<-- ``` @@ -101,9 +89,9 @@ examples/darcy/darcy2d.py:42:46 以作用在内部点上的 `InteriorConstraint` 为例，代码如下： -``` py linenums="48" +``` py linenums="51" --8<-- -examples/darcy/darcy2d.py:48:65 +examples/darcy/darcy2d.py:51:68 --8<-- ``` @@ -125,9 +113,9 @@ examples/darcy/darcy2d.py:48:65 同理，我们还需要构建矩形的四个边界的约束。但与构建 `InteriorConstraint` 约束不同的是，由于作用区域是边界，因此我们使用 `BoundaryConstraint` 类，代码如下： -``` py linenums="67" +``` py linenums="70" --8<-- -examples/darcy/darcy2d.py:67:77 +examples/darcy/darcy2d.py:70:80 --8<-- ``` @@ -143,9 +131,9 @@ lambda _in: np.sin(2.0 * np.pi * _in["x"]) * np.cos(2.0 * np.pi * _in["y"]) 在微分方程约束、边界约束、初值约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="78" +``` py linenums="81" --8<-- -examples/darcy/darcy2d.py:78:82 +examples/darcy/darcy2d.py:81:85 --8<-- ``` @@ -153,9 +141,9 @@ examples/darcy/darcy2d.py:78:82 接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用一万轮训练轮数。 -``` yaml linenums="39" +``` py linenums="87" --8<-- -examples/darcy/conf/darcy2d.yaml:39:47 +examples/darcy/darcy2d.py:87:88 --8<-- ``` @@ -163,9 +151,9 @@ examples/darcy/conf/darcy2d.yaml:39:47 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器，并配合使用机器学习中常用的 OneCycle 学习率调整策略。 -``` py linenums="84" +``` py linenums="90" --8<-- -examples/darcy/darcy2d.py:84:86 +examples/darcy/darcy2d.py:90:97 --8<-- ``` @@ -173,9 +161,9 @@ examples/darcy/darcy2d.py:84:86 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.GeometryValidator` 构建评估器。 -``` py linenums="88" +``` py linenums="99" --8<-- -examples/darcy/darcy2d.py:88:105 +examples/darcy/darcy2d.py:99:116 --8<-- ``` @@ -185,9 +173,9 @@ examples/darcy/darcy2d.py:88:105 本文中的输出数据是一个区域内的二维点集，因此我们只需要将评估的输出数据保存成 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="106" +``` py linenums="118" --8<-- -examples/darcy/darcy2d.py:106:147 +examples/darcy/darcy2d.py:118:156 --8<-- ``` @@ -197,9 +185,9 @@ examples/darcy/darcy2d.py:106:147 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估、可视化。 -``` py linenums="148" +``` py linenums="158" --8<-- -examples/darcy/darcy2d.py:148:169 +examples/darcy/darcy2d.py:158:179 --8<-- ``` @@ -207,9 +195,9 @@ examples/darcy/darcy2d.py:148:169 在使用 `Adam` 优化器训练完毕之后，我们可以将优化器更换成二阶优化器 `L-BFGS` 继续训练少量轮数（此处我们使用 `Adam` 优化轮数的 10% 即可），从而进一步提高模型精度。 -``` py linenums="172" +``` py linenums="181" --8<-- -examples/darcy/darcy2d.py:172:198 +examples/darcy/darcy2d.py:181:206 --8<-- ``` diff --git a/docs/zh/examples/deephpms.md b/docs/zh/examples/deephpms.md index 9be5e6d77..a39369673 100644 --- a/docs/zh/examples/deephpms.md +++ b/docs/zh/examples/deephpms.md @@ -2,29 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers_sine.mat -O ./datasets/DeepHPMs/burgers_sine.mat - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers.mat -O ./datasets/DeepHPMs/burgers.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers_sine.mat --output ./datasets/DeepHPMs/burgers_sine.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers.mat --output ./datasets/DeepHPMs/burgers.mat - python burgers.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers_sine.mat -O ./datasets/DeepHPMs/burgers_sine.mat - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers.mat -O ./datasets/DeepHPMs/burgers.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers_sine.mat --output ./datasets/DeepHPMs/burgers_sine.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers.mat --output ./datasets/DeepHPMs/burgers.mat - python burgers.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/DeepHPMs/burgers_pretrained.pdparams - ``` - ## 1. 背景简介 求解偏微分方程(PDE) 是一类基础的物理问题，在过去几十年里，以有限差分(FDM)、有限体积(FVM)、有限元(FEM)为代表的多种偏微分方程组数值解法趋于成熟。随着人工智能技术的高速发展，利用深度学习求解偏微分方程成为新的研究趋势。PINNs(Physics-informed neural networks) 是一种加入物理约束的深度学习网络，因此与纯数据驱动的神经网络学习相比，PINNs 可以用更少的数据样本学习到更具泛化能力的模型，其应用范围包括但不限于流体力学、热传导、电磁场、量子力学等领域。 @@ -62,9 +39,9 @@ $$ 运行本问题代码前请下载 [模拟数据集1](https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers_sine.mat) 和 [模拟数据集2](https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepHPMs/burgers.mat)， 下载后分别存放在路径： -``` yaml linenums="26" +``` py linenums="55" --8<-- -examples/deephpms/conf/burgers.yaml:26:27 +examples/deephpms/burgers.py:55:56 --8<-- ``` @@ -80,9 +57,9 @@ Net1 通过数据驱动的方式，使用输入的某种模拟情况 1 下的少 因为训练中后一个阶段网络需要使用前一个阶段网络的前向推理值，因此本问题使用 Model List 来实现，上式中 $f_1,f_2,f_3$ 分别为一个 MLP 模型，三者共同构成了一个 Model List，用 PaddleScience 代码表示如下 -``` py linenums="99" +``` py linenums="68" --8<-- -examples/deephpms/burgers.py:99:100 +examples/deephpms/burgers.py:68:71 --8<-- ``` @@ -92,25 +69,25 @@ examples/deephpms/burgers.py:99:100 对于 Net1，输入为 $(x, t)$ 本来不需要 transform，但由于训练中根据数据的定义域对输入数据进行了数值变换，因此同样需要transform，同样，Net3 也需要对输入进行数值变换的 transform -``` py linenums="72" +``` py linenums="73" --8<-- -examples/deephpms/burgers.py:72:77 +examples/deephpms/burgers.py:73:79 --8<-- ``` 对于 Net2，因为它的输入为 $u, u_x, u_{xx}$ 而 $u$ 为其他两个网络的输出，只要进行 Net2 的前向推理，就需要 transform，因此需要两种 transform。同时，在训练 Net3 之前，需要重新注册 transform -``` py linenums="88" +``` py linenums="81" --8<-- -examples/deephpms/burgers.py:88:92 +examples/deephpms/burgers.py:81:94 --8<-- ``` 然后依次注册 transform 后，将3 个 MLP 模型组成 Model List -``` py linenums="100" +``` py linenums="96" --8<-- -examples/deephpms/burgers.py:95:100 +examples/deephpms/burgers.py:96:102 --8<-- ``` @@ -118,7 +95,7 @@ examples/deephpms/burgers.py:95:100 ``` py linenums="243" --8<-- -examples/deephpms/burgers.py:236:237 +examples/deephpms/burgers.py:243:244 --8<-- ``` @@ -128,17 +105,17 @@ examples/deephpms/burgers.py:236:237 我们需要指定问题相关的参数，如数据集路径、输出文件路径、定义域的值等 -``` yaml linenums="26" +``` py linenums="53" --8<-- -examples/deephpms/conf/burgers.yaml:26:33 +examples/deephpms/burgers.py:53:66 --8<-- ``` 同时需要指定训练轮数和学习率等超参数 -``` yaml linenums="57" +``` py linenums="104" --8<-- -examples/deephpms/conf/burgers.yaml:57:61 +examples/deephpms/burgers.py:104:107 --8<-- ``` @@ -146,9 +123,9 @@ examples/deephpms/conf/burgers.yaml:57:61 本问题提供了两种优化器，分别为 Adam 优化器和 LBFGS 优化器，训练时只选择其中一种，需要将另一种优化器注释掉。 -``` py linenums="103" +``` py linenums="109" --8<-- -examples/deephpms/burgers.py:103:111 +examples/deephpms/burgers.py:109:118 --8<-- ``` @@ -158,9 +135,9 @@ examples/deephpms/burgers.py:103:111 无监督仍然可以采用监督约束 `SupervisedConstraint`，在定义约束之前，需要给监督约束指定文件路径等数据读取配置，因为数据集中没有标签数据，因此在数据读取时我们需要使用训练数据充当标签数据，并注意在之后不要使用这部分“假的”标签数据，例如 -``` py linenums="115" +``` py linenums="180" --8<-- -examples/deephpms/burgers.py:115:123 +examples/deephpms/burgers.py:180:188 --8<-- ``` @@ -170,9 +147,9 @@ examples/deephpms/burgers.py:115:123 第一阶段对 Net1 的训练是纯监督学习，此处采用监督约束 `SupervisedConstraint` -``` py linenums="125" +``` py linenums="121" --8<-- -examples/deephpms/burgers.py:125:131 +examples/deephpms/burgers.py:121:138 --8<-- ``` @@ -196,9 +173,9 @@ examples/deephpms/burgers.py:125:131 第二阶段对 Net2 的训练是无监督学习，但仍可采用监督约束 `SupervisedConstraint`，要注意上述提到的给定“假的”标签数据 -``` py linenums="144" +``` py linenums="179" --8<-- -examples/deephpms/burgers.py:144:151 +examples/deephpms/burgers.py:179:199 --8<-- ``` @@ -210,9 +187,9 @@ examples/deephpms/burgers.py:144:151 第三阶段 Net3 的训练复杂，包含了对部分初始点的监督学习、与 PDE 有关的无监督学习以及与边界条件有关的无监督学习，这里仍采用监督约束 `SupervisedConstraint`，同样要注意给定“假的”标签数据，各参数含义同上 -``` py linenums="183" +``` py linenums="246" --8<-- -examples/deephpms/burgers.py:183:192 +examples/deephpms/burgers.py:246:303 --8<-- ``` @@ -226,9 +203,9 @@ examples/deephpms/burgers.py:183:192 评价指标 `metric` 为 `L2` 正则化函数 -``` py linenums="205" +``` py linenums="140" --8<-- -examples/deephpms/burgers.py:205:215 +examples/deephpms/burgers.py:140:158 --8<-- ``` @@ -236,9 +213,9 @@ examples/deephpms/burgers.py:205:215 评价指标 `metric` 为 `FunctionalMetric`，这是 PaddleScience 预留的自定义 metric 函数类，该类支持编写代码时自定义 metric 的计算方法，而不是使用诸如 `MSE`、 `L2` 等现有方法。自定义 metric 函数代码请参考下一部分 [自定义 loss 和 metric](#38)。 -``` py linenums="268" +``` py linenums="201" --8<-- -examples/deephpms/burgers.py:268:291 +examples/deephpms/burgers.py:201:222 --8<-- ``` @@ -246,9 +223,9 @@ examples/deephpms/burgers.py:268:291 因为第三阶段评价时只需要对训练得到的点的值进行评价，而不需要对边界条件满足程度或 PDE 满足程度进行评价，因此评价指标 `metric` 为 `L2` 正则化函数 -``` py linenums="309" +``` py linenums="305" --8<-- -examples/deephpms/burgers.py:309:318 +examples/deephpms/burgers.py:305:325 --8<-- ``` @@ -260,25 +237,25 @@ examples/deephpms/burgers.py:309:318 与 PDE 相关的自定义 loss 函数为 -``` py linenums="28" +``` py linenums="25" --8<-- -examples/deephpms/burgers.py:28:30 +examples/deephpms/burgers.py:25:27 --8<-- ``` 与 PDE 相关的自定义 metric 函数为 -``` py linenums="33" +``` py linenums="30" --8<-- -examples/deephpms/burgers.py:33:38 +examples/deephpms/burgers.py:30:35 --8<-- ``` 与边界条件相关的自定义 loss 函数为 -``` py linenums="41" +``` py linenums="38" --8<-- -examples/deephpms/burgers.py:41:52 +examples/deephpms/burgers.py:38:49 --8<-- ``` @@ -288,25 +265,25 @@ examples/deephpms/burgers.py:41:52 第一阶段训练、评估 -``` py linenums="154" +``` py linenums="160" --8<-- -examples/deephpms/burgers.py:154:169 +examples/deephpms/burgers.py:160:176 --8<-- ``` 第二阶段训练、评估 -``` py linenums="218" +``` py linenums="224" --8<-- -examples/deephpms/burgers.py:218:233 +examples/deephpms/burgers.py:224:240 --8<-- ``` 第三阶段训练、评估 -``` py linenums="321" +``` py linenums="327" --8<-- -examples/deephpms/burgers.py:321:336 +examples/deephpms/burgers.py:327:343 --8<-- ``` diff --git a/docs/zh/examples/deeponet.md b/docs/zh/examples/deeponet.md index a28a322cd..358825301 100644 --- a/docs/zh/examples/deeponet.md +++ b/docs/zh/examples/deeponet.md @@ -2,30 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepONet/antiderivative_unaligned_train.npz - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepONet/antiderivative_unaligned_test.npz - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/deeponet/antiderivative_unaligned_train.npz --output antiderivative_unaligned_train.npz - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/deeponet/antiderivative_unaligned_test.npz --output antiderivative_unaligned_test.npz - python deeponet.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepONet/antiderivative_unaligned_train.npz - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/DeepONet/antiderivative_unaligned_test.npz - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/deeponet/antiderivative_unaligned_train.npz --output antiderivative_unaligned_train.npz - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/deeponet/antiderivative_unaligned_test.npz --output antiderivative_unaligned_test.npz - python deeponet.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/deeponet/deeponet_pretrained.pdparams - ``` - ## 1. 背景简介 根据机器学习领域的万能近似定理，一个神经网络模型不仅可以拟合输入数据到输出数据的函数映射关系，也可以扩展到对函数与函数之间的映射关系进行拟合，称之为“算子”学习。 @@ -101,7 +77,7 @@ $$ ``` py linenums="27" --8<-- -examples/operator_learning/deeponet.py:27:27 +examples/operator_learning/deeponet.py:27:43 --8<-- ``` @@ -113,9 +89,9 @@ examples/operator_learning/deeponet.py:27:27 在定义约束之前，需要给监督约束指定文件路径等数据读取配置，包括文件路径、输入数据字段名、标签数据字段名、数据转换前后的别名字典。 -``` py linenums="30" +``` py linenums="45" --8<-- -examples/operator_learning/deeponet.py:30:38 +examples/operator_learning/deeponet.py:45:55 --8<-- ``` @@ -123,9 +99,9 @@ examples/operator_learning/deeponet.py:30:38 由于我们以监督学习方式进行训练，此处采用监督约束 `SupervisedConstraint`： -``` py linenums="40" +``` py linenums="57" --8<-- -examples/operator_learning/deeponet.py:40:44 +examples/operator_learning/deeponet.py:57:61 --8<-- ``` @@ -137,19 +113,19 @@ examples/operator_learning/deeponet.py:40:44 在监督约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="45" +``` py linenums="62" --8<-- -examples/operator_learning/deeponet.py:45:46 +examples/operator_learning/deeponet.py:62:63 --8<-- ``` ### 3.4 超参数设定 -接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用一万轮训练轮数，并每隔 500 个 epochs 评估一次模型精度。 +接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用十万轮训练轮数，并每隔 500 个 epochs 评估一次模型精度。 -``` yaml linenums="49" +``` py linenums="65" --8<-- -examples/operator_learning/conf/deeponet.yaml:49:55 +examples/operator_learning/deeponet.py:65:66 --8<-- ``` @@ -157,9 +133,9 @@ examples/operator_learning/conf/deeponet.yaml:49:55 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器，学习率设置为 `0.001`。 -``` py linenums="48" +``` py linenums="68" --8<-- -examples/operator_learning/deeponet.py:48:49 +examples/operator_learning/deeponet.py:68:69 --8<-- ``` @@ -167,9 +143,9 @@ examples/operator_learning/deeponet.py:48:49 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.SupervisedValidator` 构建评估器。 -``` py linenums="51" +``` py linenums="71" --8<-- -examples/operator_learning/deeponet.py:51:60 +examples/operator_learning/deeponet.py:71:88 --8<-- ``` @@ -181,9 +157,9 @@ examples/operator_learning/deeponet.py:51:60 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。 -``` py linenums="71" +``` py linenums="90" --8<-- -examples/operator_learning/deeponet.py:71:90 +examples/operator_learning/deeponet.py:90:123 --8<-- ``` @@ -191,9 +167,9 @@ examples/operator_learning/deeponet.py:71:90 在模型训练完毕之后，我们可以手动构造 $u$、$y$ 并在适当范围内进行离散化，得到对应输入数据，继而预测出 $G(u)(y)$，并和 $G(u)$ 的标准解共同绘制图像，进行对比。（此处我们构造了 9 组 $u-G(u)$ 函数对）进行测试 -``` py linenums="92" +``` py linenums="125" --8<-- -examples/operator_learning/deeponet.py:92:151 +examples/operator_learning/deeponet.py:125: --8<-- ``` diff --git a/docs/zh/examples/hpinns.md b/docs/zh/examples/hpinns.md index 13025d715..2385b9942 100644 --- a/docs/zh/examples/hpinns.md +++ b/docs/zh/examples/hpinns.md @@ -2,30 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - # linux - wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_train.mat - wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_valid.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_train.mat --output ./datasets/hpinns_holo_train.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_valid.mat --output ./datasets/hpinns_holo_valid.mat - python holography.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_train.mat - wget -P ./datasets/ https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_valid.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_train.mat --output ./datasets/hpinns_holo_train.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/hPINNs/hpinns_holo_valid.mat --output ./datasets/hpinns_holo_valid.mat - python holography.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/hpinns/hpinns_pretrained.pdparams - ``` - ## 1. 背景简介 求解偏微分方程(PDE) 是一类基础的物理问题，在过去几十年里，以有限差分(FDM)、有限体积(FVM)、有限元(FEM)为代表的多种偏微分方程组数值解法趋于成熟。随着人工智能技术的高速发展，利用深度学习求解偏微分方程成为新的研究趋势。PINNs(Physics-informed neural networks) 是一种加入物理约束的深度学习网络，因此与纯数据驱动的神经网络学习相比，PINNs 可以用更少的数据样本学习到更具泛化能力的模型，其应用范围包括但不限于流体力学、热传导、电磁场、量子力学等领域。 @@ -108,9 +84,9 @@ $$ 上式中 $f_1,f_2,f_3$ 分别为一个 MLP 模型，三者共同构成了一个 Model List，用 PaddleScience 代码表示如下 -``` py linenums="42" +``` py linenums="43" --8<-- -examples/hpinns/holography.py:42:44 +examples/hpinns/holography.py:43:51 --8<-- ``` @@ -129,9 +105,9 @@ examples/hpinns/functions.py:49:92 需要对每个 MLP 模型分别注册相应的 transform ，然后将 3 个 MLP 模型组成 Model List -``` py linenums="50" +``` py linenums="59" --8<-- -examples/hpinns/holography.py:50:59 +examples/hpinns/holography.py:59:68 --8<-- ``` @@ -141,15 +117,15 @@ examples/hpinns/holography.py:50:59 我们需要指定问题相关的参数，如通过 `train_mode` 参数指定应用增强的拉格朗日方法的硬约束进行训练 -``` py linenums="35" +``` py linenums="31" --8<-- -examples/hpinns/holography.py:35:40 +examples/hpinns/holography.py:31:41 --8<-- ``` -``` py linenums="46" +``` py linenums="53" --8<-- -examples/hpinns/holography.py:46:48 +examples/hpinns/holography.py:53:57 --8<-- ``` @@ -165,9 +141,15 @@ $\mu_k = \beta \mu_{k-1}$, $\lambda_k = \beta \lambda_{k-1}$ 同时需要指定训练轮数和学习率等超参数 -``` yaml linenums="53" +``` py linenums="70" +--8<-- +examples/hpinns/holography.py:70:72 +--8<-- +``` + +``` py linenums="212" --8<-- -examples/hpinns/conf/hpinns.yaml:53:61 +examples/hpinns/holography.py:212:214 --8<-- ``` @@ -175,15 +157,15 @@ examples/hpinns/conf/hpinns.yaml:53:61 训练分为两个阶段，先使用 Adam 优化器进行大致训练，再使用 LBFGS 优化器逼近最优点，因此需要两个优化器，这也对应了上一部分超参数中的两种 `EPOCHS` 值 -``` py linenums="62" +``` py linenums="74" --8<-- -examples/hpinns/holography.py:62:64 +examples/hpinns/holography.py:74:75 --8<-- ``` -``` py linenums="203" +``` py linenums="216" --8<-- -examples/hpinns/holography.py:203:205 +examples/hpinns/holography.py:216:219 --8<-- ``` @@ -193,9 +175,9 @@ examples/hpinns/holography.py:203:205 虽然我们不是以监督学习方式进行训练，但此处仍然可以采用监督约束 `SupervisedConstraint`，在定义约束之前，需要给监督约束指定文件路径等数据读取配置，因为数据集中没有标签数据，因此在数据读取时我们需要使用训练数据充当标签数据，并注意在之后不要使用这部分“假的”标签数据。 -``` py linenums="102" +``` py linenums="113" --8<-- -examples/hpinns/holography.py:102:107 +examples/hpinns/holography.py:113:118 --8<-- ``` @@ -203,9 +185,9 @@ examples/hpinns/holography.py:102:107 下面是约束等具体内容，要注意上述提到的给定“假的”标签数据： -``` py linenums="66" +``` py linenums="77" --8<-- -examples/hpinns/holography.py:66:127 +examples/hpinns/holography.py:77:138 --8<-- ``` @@ -225,9 +207,9 @@ examples/hpinns/holography.py:66:127 在约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="128" +``` py linenums="139" --8<-- -examples/hpinns/holography.py:128:131 +examples/hpinns/holography.py:139:142 --8<-- ``` @@ -235,9 +217,9 @@ examples/hpinns/holography.py:128:131 与约束同理，虽然本问题使用无监督学习，但仍可以使用 `ppsci.validate.SupervisedValidator` 构建评估器。 -``` py linenums="133" +``` py linenums="144" --8<-- -examples/hpinns/holography.py:133:181 +examples/hpinns/holography.py:144:192 --8<-- ``` @@ -267,9 +249,9 @@ examples/hpinns/functions.py:320:336 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。 -``` py linenums="183" +``` py linenums="194" --8<-- -examples/hpinns/holography.py:183:200 +examples/hpinns/holography.py:194:210 --8<-- ``` @@ -279,9 +261,9 @@ examples/hpinns/holography.py:183:200 PaddleScience 中提供了可视化器，但由于本问题图片数量较多且较为复杂，代码中自定义了可视化函数，调用自定义函数即可实现可视化 -``` py linenums="279" +``` py linenums="289" --8<-- -examples/hpinns/holography.py:279:292 +examples/hpinns/holography.py:289: --8<-- ``` diff --git a/docs/zh/examples/labelfree_DNN_surrogate.md b/docs/zh/examples/labelfree_DNN_surrogate.md index cd81bd64c..e9a78ec77 100644 --- a/docs/zh/examples/labelfree_DNN_surrogate.md +++ b/docs/zh/examples/labelfree_DNN_surrogate.md @@ -1,17 +1,5 @@ # LabelFree-DNN-Surrogate (Aneurysm flow & Pipe flow) -=== "模型训练命令" - - ``` sh - python poiseuille_flow.py - ``` - -=== "模型评估命令" - - ``` sh - python poiseuille_flow.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/poiseuille_flow/poiseuille_flow_pretrained.pdparams - ``` - ## 1. 背景简介 流体动力学问题的数值模拟主要依赖于使用多项式将控制方程在空间或/和时间上离散化为有限维代数系统。由于物理的多尺度特性和对复杂几何体进行网格划分的敏感性，这样的过程对于大多数实时应用程序（例如，临床诊断和手术计划）和多查询分析（例如，优化设计和不确定性量化）。在本文中，我们提供了一种物理约束的 DL 方法，用于在不依赖任何模拟数据的情况下对流体流动进行代理建模。 具体来说，设计了一种结构化深度神经网络 (DNN) 架构来强制执行初始条件和边界条件，并将控制偏微分方程（即 Navier-Stokes 方程）纳入 DNN的损失中以驱动训练。 对与血液动力学应用相关的许多内部流动进行了数值实验，并研究了流体特性和域几何中不确定性的前向传播。结果表明，DL 代理近似与第一原理数值模拟之间的流场和前向传播不确定性非常吻合。 @@ -91,15 +79,15 @@ $$ 上式中 $f_1, f_2, f_3$ 即为 MLP 模型本身，$transform_{input}, transform_{output}$, 表示施加额外的结构化自定义层，用于施加约束和丰富输入，用 PaddleScience 代码表示如下: -``` py linenums="78" +``` py linenums="95" --8<-- -examples/pipe/poiseuille_flow.py:78:80 +examples/pipe/poiseuille_flow.py:95:98 --8<-- ``` -``` py linenums="105" +``` py linenums="123" --8<-- -examples/pipe/poiseuille_flow.py:105:111 +examples/pipe/poiseuille_flow.py:123:129 --8<-- ``` @@ -111,9 +99,9 @@ examples/pipe/poiseuille_flow.py:105:111 由于本案例使用的是 Navier-Stokes 方程的2维稳态形式，因此可以直接使用 PaddleScience 内置的 `NavierStokes`。 -``` py linenums="117" +``` py linenums="134" --8<-- -examples/pipe/poiseuille_flow.py:117:121 +examples/pipe/poiseuille_flow.py:134:139 --8<-- ``` @@ -123,9 +111,9 @@ examples/pipe/poiseuille_flow.py:117:121 本文中本案例的计算域和参数自变量 $\nu$ 由`numpy`随机数生成的点云构成，因此可以直接使用 PaddleScience 内置的点云几何 `PointCloud` 组合成空间的 `Geometry` 计算域。 -``` py linenums="52" +``` py linenums="67" --8<-- -examples/pipe/poiseuille_flow.py:52:75 +examples/pipe/poiseuille_flow.py:67:94 --8<-- ``` @@ -187,9 +175,9 @@ examples/pipe/poiseuille_flow.py:52:75 以作用在流体域内部点上的 `InteriorConstraint` 为例，代码如下： - ``` py linenums="128" + ``` py linenums="145" --8<-- - examples/pipe/poiseuille_flow.py:128:146 + examples/pipe/poiseuille_flow.py:145:164 --8<-- ``` @@ -209,13 +197,19 @@ examples/pipe/poiseuille_flow.py:52:75 接下来我们需要指定训练轮数和学习率，使用3000轮训练轮数，学习率设为 0.005。 +``` py linenums="168" +--8<-- +examples/pipe/poiseuille_flow.py:168:168 +--8<-- +``` + #### 2.2.6 优化器构建 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 -``` py linenums="127" +``` py linenums="131" --8<-- -examples/pipe/poiseuille_flow.py:114:114 +examples/pipe/poiseuille_flow.py:131:132 --8<-- ``` @@ -223,9 +217,9 @@ examples/pipe/poiseuille_flow.py:114:114 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练。 -``` py linenums="152" +``` py linenums="170" --8<-- -examples/pipe/poiseuille_flow.py:152:164 +examples/pipe/poiseuille_flow.py:170:183 --8<-- ``` @@ -235,9 +229,9 @@ examples/pipe/poiseuille_flow.py:152:164 2. 当我们选取截断高斯分布的动力粘性系数 ${\nu}$ 采样(均值为 $\hat{\nu} = 10^{−3}$， 方差 $\sigma_{\nu}​=2.67×10^{−4}$)，中心处速度的概率密度函数和解析解对比 -``` py linenums="166" +``` py linenums="185" --8<-- -examples/pipe/poiseuille_flow.py:166:274 +examples/pipe/poiseuille_flow.py:185:293 --8<-- ``` @@ -350,7 +344,7 @@ $$ 上式中 $f_1, f_2, f_3$ 即为 MLP 模型本身，$transform_{input}, transform_{output}$, 表示施加额外的结构化自定义层，用于施加约束和链接输入，用 PaddleScience 代码表示如下: -``` py linenums="119" +``` py linenums="33" --8<-- examples/aneurysm/aneurysm_flow.py:119:128 --8<-- @@ -482,12 +476,6 @@ examples/aneurysm/aneurysm_flow.py:204:204 --8<-- ``` -``` py linenums="166" ---8<-- -examples/aneurysm/aneurysm_flow.py:166:166 ---8<-- -``` - #### 3.2.6 优化器构建 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 diff --git a/docs/zh/examples/laplace2d.md b/docs/zh/examples/laplace2d.md index d96bdd896..1af861c2c 100644 --- a/docs/zh/examples/laplace2d.md +++ b/docs/zh/examples/laplace2d.md @@ -2,12 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - python laplace2d.py - ``` - ## 1. 背景简介 拉普拉斯方程由法国数学家拉普拉斯首先提出而得名，该方程在许多领域都有重要应用，例如电磁学、天文学和流体力学等。在实际应用中，拉普拉斯方程的求解往往是一个复杂的数学问题。对于一些具有特定边界条件和初始条件的实际问题，可以通过特定的数值方法（如有限元方法、有限差分方法等）来求解拉普拉斯方程。对于一些复杂的问题，可能需要采用更高级的数值方法或者借助高性能计算机进行计算。 @@ -38,9 +32,9 @@ $$ 上式中 $f$ 即为 MLP 模型本身，用 PaddleScience 代码表示如下 -``` py linenums="32" +``` py linenums="35" --8<-- -examples/laplace/laplace2d.py:32:33 +examples/laplace/laplace2d.py:35:36 --8<-- ``` @@ -52,9 +46,9 @@ examples/laplace/laplace2d.py:32:33 由于 2D-Laplace 使用的是 Laplace 方程的2维形式，因此可以直接使用 PaddleScience 内置的 `Laplace`，指定该类的参数 `dim` 为2。 -``` py linenums="35" +``` py linenums="38" --8<-- -examples/laplace/laplace2d.py:35:36 +examples/laplace/laplace2d.py:38:39 --8<-- ``` @@ -63,9 +57,9 @@ examples/laplace/laplace2d.py:35:36 本文中 2D Laplace 问题作用在以 (0.0, 0.0), (1.0, 1.0) 为对角线的二维矩形区域， 因此可以直接使用 PaddleScience 内置的空间几何 `Rectangle` 作为计算域。 -``` py linenums="38" +``` py linenums="41" --8<-- -examples/laplace/laplace2d.py:38:43 +examples/laplace/laplace2d.py:41:42 --8<-- ``` @@ -75,9 +69,9 @@ examples/laplace/laplace2d.py:38:43 在定义约束之前，需要给每一种约束指定采样点个数，表示每一种约束在其对应计算域内采样数据的数量，以及通用的采样配置。 -``` yaml linenums="26" +``` py linenums="56" --8<-- -examples/laplace/conf/laplace2d.yaml:26:27 +examples/laplace/laplace2d.py:56:58 --8<-- ``` @@ -85,9 +79,9 @@ examples/laplace/conf/laplace2d.yaml:26:27 以作用在内部点上的 `InteriorConstraint` 为例，代码如下： -``` py linenums="60" +``` py linenums="61" --8<-- -examples/laplace/laplace2d.py:60:68 +examples/laplace/laplace2d.py:61:69 --8<-- ``` @@ -109,9 +103,9 @@ examples/laplace/laplace2d.py:60:68 同理，我们还需要构建矩形的四个边界的约束。但与构建 `InteriorConstraint` 约束不同的是，由于作用区域是边界，因此我们使用 `BoundaryConstraint` 类，代码如下： -``` py linenums="69" +``` py linenums="70" --8<-- -examples/laplace/laplace2d.py:69:76 +examples/laplace/laplace2d.py:70:77 --8<-- ``` @@ -119,9 +113,9 @@ examples/laplace/laplace2d.py:69:76 第二个参数是指我们约束对象的真值如何获得，这里我们直接通过其解析解进行计算，定义解析解的代码如下： -``` py linenums="45" +``` py linenums="44" --8<-- -examples/laplace/laplace2d.py:45:49 +examples/laplace/laplace2d.py:44:48 --8<-- ``` @@ -129,11 +123,11 @@ examples/laplace/laplace2d.py:45:49 ### 3.5 超参数设定 -接下来我们需要在配置文件中指定训练轮数，此处我们按实验经验，使用两万轮训练轮数，评估间隔为两百轮。 +接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用两万轮训练轮数，评估间隔为两百轮。 -``` py linenums="41" +``` py linenums="26" --8<-- -examples/laplace/conf/laplace2d.yaml:41:46 +examples/laplace/laplace2d.py:26:29 --8<-- ``` @@ -141,9 +135,9 @@ examples/laplace/conf/laplace2d.yaml:41:46 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 -``` py linenums="83" +``` py linenums="84" --8<-- -examples/laplace/laplace2d.py:83:84 +examples/laplace/laplace2d.py:84:85 --8<-- ``` @@ -151,9 +145,9 @@ examples/laplace/laplace2d.py:83:84 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.GeometryValidator` 构建评估器。 -``` py linenums="86" +``` py linenums="87" --8<-- -examples/laplace/laplace2d.py:86:100 +examples/laplace/laplace2d.py:87:102 --8<-- ``` @@ -163,9 +157,9 @@ examples/laplace/laplace2d.py:86:100 本文中的输出数据是一个区域内的二维点集，因此我们只需要将评估的输出数据保存成 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="103" +``` py linenums="104" --8<-- -examples/laplace/laplace2d.py:103:112 +examples/laplace/laplace2d.py:104:113 --8<-- ``` @@ -173,9 +167,9 @@ examples/laplace/laplace2d.py:103:112 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估、可视化。 -``` py linenums="114" +``` py linenums="115" --8<-- -examples/laplace/laplace2d.py:114:134 +examples/laplace/laplace2d.py:115: --8<-- ``` diff --git a/docs/zh/examples/ldc2d_steady.md b/docs/zh/examples/ldc2d_steady.md index 6ad3a45b1..7a721a50c 100644 --- a/docs/zh/examples/ldc2d_steady.md +++ b/docs/zh/examples/ldc2d_steady.md @@ -2,11 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - ``` sh - python ldc2d_steady_Re10.py - ``` - ## 1. 背景简介 顶盖方腔驱动流LDC问题在许多领域中都有应用。例如，这个问题可以用于计算流体力学（CFD）领域中验证计算方法的有效性。虽然这个问题的边界条件相对简单，但是其流动特性却非常复杂。在顶盖驱动流LDC中，顶壁朝x方向以U=1的速度移动，而其他三个壁则被定义为无滑移边界条件，即速度为零。 @@ -196,7 +191,7 @@ examples/ldc/ldc2d_steady_Re10.py:36:37 ``` py linenums="39" --8<-- -examples/ldc/ldc2d_steady_Re10.py:39:49 +examples/ldc/ldc2d_steady_Re10.py:39:50 --8<-- ``` @@ -204,18 +199,22 @@ examples/ldc/ldc2d_steady_Re10.py:39:49 以作用在矩形内部点上的 `InteriorConstraint` 为例，代码如下： -``` py linenums="51" +``` py linenums="63" # set constraint -pde = ppsci.constraint.InteriorConstraint( - equation["NavierStokes"].equations, - {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, - geom["rect"], - {**train_dataloader_cfg, "batch_size": NPOINT_PDE}, - ppsci.loss.MSELoss("sum"), - evenly=True, - weight_dict=cfg.TRAIN.weight.pde, # (1) - name="EQ", -) +pde_constraint = ppsci.constraint.InteriorConstraint( + equation["NavierStokes"].equations, + {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, + geom["rect"], + {**train_dataloader_cfg, "batch_size": npoint_pde}, + ppsci.loss.MSELoss("sum"), + evenly=True, + weight_dict={ + "continuity": 0.0001, # (1) + "momentum_x": 0.0001, + "momentum_y": 0.0001, + }, + name="EQ", + ) ``` 1. 本案例中PDE约束损失的数量级远大于边界约束损失，因此需要给PDE约束权重设置一个较小的值，有利于模型收敛 @@ -246,27 +245,27 @@ pde = ppsci.constraint.InteriorConstraint( 由于 `BoundaryConstraint` 默认会在所有边界上进行采样，而我们需要对四个边界分别施加约束，因此需通过设置 `criteria` 参数，进一步细化出四个边界，如上边界就是符合 $y = 0.05$ 的边界点集 -``` py linenums="62" +``` py linenums="67" --8<-- -examples/ldc/ldc2d_steady_Re10.py:62:97 +examples/ldc/ldc2d_steady_Re10.py:67:102 --8<-- ``` 在微分方程约束、边界约束、初值约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="98" +``` py linenums="103" --8<-- -examples/ldc/ldc2d_steady_Re10.py:98:105 +examples/ldc/ldc2d_steady_Re10.py:103:110 --8<-- ``` ### 3.5 超参数设定 -接下来需要在配置文件中指定训练轮数，此处我们按实验经验，使用两万轮训练轮数和带有 warmup 的 Cosine 余弦衰减学习率。 +接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用两万轮训练轮数和带有 warmup 的 Cosine 余弦衰减学习率。 -``` yaml linenums="39" +``` py linenums="112" --8<-- -examples/ldc/conf/ldc2d_steady_Re10.yaml:39:42 +examples/ldc/ldc2d_steady_Re10.py:112:119 --8<-- ``` @@ -274,9 +273,9 @@ examples/ldc/conf/ldc2d_steady_Re10.yaml:39:42 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 -``` py linenums="107" +``` py linenums="121" --8<-- -examples/ldc/ldc2d_steady_Re10.py:107:112 +examples/ldc/ldc2d_steady_Re10.py:121:122 --8<-- ``` @@ -284,9 +283,9 @@ examples/ldc/ldc2d_steady_Re10.py:107:112 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.GeometryValidator` 构建评估器。 -``` py linenums="114" +``` py linenums="124" --8<-- -examples/ldc/ldc2d_steady_Re10.py:114:131 +examples/ldc/ldc2d_steady_Re10.py:124:141 --8<-- ``` @@ -308,9 +307,9 @@ examples/ldc/ldc2d_steady_Re10.py:114:131 本文中的输出数据是一个区域内的二维点集，因此我们只需要将评估的输出数据保存成 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="133" +``` py linenums="143" --8<-- -examples/ldc/ldc2d_steady_Re10.py:133:143 +examples/ldc/ldc2d_steady_Re10.py:143:153 --8<-- ``` @@ -318,9 +317,9 @@ examples/ldc/ldc2d_steady_Re10.py:133:143 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估、可视化。 -``` py linenums="145" +``` py linenums="155" --8<-- -examples/ldc/ldc2d_steady_Re10.py:145:167 +examples/ldc/ldc2d_steady_Re10.py:155: --8<-- ``` diff --git a/docs/zh/examples/ldc2d_unsteady.md b/docs/zh/examples/ldc2d_unsteady.md index dda32b5cf..4e219bb1e 100644 --- a/docs/zh/examples/ldc2d_unsteady.md +++ b/docs/zh/examples/ldc2d_unsteady.md @@ -2,11 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - ``` sh - python ldc2d_unsteady_Re10.py - ``` - ## 1. 背景简介 顶盖方腔驱动流LDC问题在许多领域中都有应用。例如，这个问题可以用于计算流体力学（CFD）领域中验证计算方法的有效性。虽然这个问题的边界条件相对简单，但是其流动特性却非常复杂。在顶盖驱动流LDC中，顶壁朝x方向以U=1的速度移动，而其他三个壁则被定义为无滑移边界条件，即速度为零。 @@ -206,7 +201,7 @@ examples/ldc/ldc2d_unsteady_Re10.py:36:44 ``` py linenums="46" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:46:58 +examples/ldc/ldc2d_unsteady_Re10.py:46:60 --8<-- ``` @@ -214,16 +209,20 @@ examples/ldc/ldc2d_unsteady_Re10.py:46:58 以作用在矩形内部点上的 `InteriorConstraint` 为例，代码如下： -``` py linenums="60" +``` py linenums="62" # set constraint -pde = ppsci.constraint.InteriorConstraint( +pde_constraint = ppsci.constraint.InteriorConstraint( equation["NavierStokes"].equations, {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, geom["time_rect"], {**train_dataloader_cfg, "batch_size": NPOINT_PDE * NTIME_PDE}, ppsci.loss.MSELoss("sum"), evenly=True, - weight_dict=cfg.TRAIN.weight.pde, # (1) + weight_dict={ + "continuity": 0.0001, # (1) + "momentum_x": 0.0001, + "momentum_y": 0.0001, + }, name="EQ", ) ``` @@ -258,9 +257,9 @@ pde = ppsci.constraint.InteriorConstraint( 由于 `BoundaryConstraint` 默认会在所有边界上进行采样，而我们需要对四个边界分别施加约束，因此需通过设置 `criteria` 参数，进一步细化出四个边界，如上边界就是符合 $y = 0.05$ 的边界点集 -``` py linenums="71" +``` py linenums="77" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:71:106 +examples/ldc/ldc2d_unsteady_Re10.py:77:112 --8<-- ``` @@ -268,27 +267,27 @@ examples/ldc/ldc2d_unsteady_Re10.py:71:106 最后我们还需要对 $t=t_0$ 时刻的矩形内部点施加 N-S 方程约束，代码如下： -``` py linenums="107" +``` py linenums="113" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:107:115 +examples/ldc/ldc2d_unsteady_Re10.py:113:121 --8<-- ``` 在微分方程约束、边界约束、初值约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="116" +``` py linenums="122" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:116:124 +examples/ldc/ldc2d_unsteady_Re10.py:122:130 --8<-- ``` ### 3.5 超参数设定 -接下来需要在配置文件中指定训练轮数，此处我们按实验经验，使用两万轮训练轮数和带有 warmup 的 Cosine 余弦衰减学习率。 +接下来我们需要指定训练轮数和学习率，此处我们按实验经验，使用两万轮训练轮数和带有 warmup 的 Cosine 余弦衰减学习率。 -``` yaml linenums="40" +``` py linenums="132" --8<-- -examples/ldc/conf/ldc2d_unsteady_Re10.yaml:40:43 +examples/ldc/ldc2d_unsteady_Re10.py:132:139 --8<-- ``` @@ -296,9 +295,9 @@ examples/ldc/conf/ldc2d_unsteady_Re10.yaml:40:43 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。 -``` py linenums="132" +``` py linenums="141" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:132:133 +examples/ldc/ldc2d_unsteady_Re10.py:141:142 --8<-- ``` @@ -306,9 +305,9 @@ examples/ldc/ldc2d_unsteady_Re10.py:132:133 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.GeometryValidator` 构建评估器。 -``` py linenums="135" +``` py linenums="144" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:135:153 +examples/ldc/ldc2d_unsteady_Re10.py:144:162 --8<-- ``` @@ -330,9 +329,9 @@ examples/ldc/ldc2d_unsteady_Re10.py:135:153 本文中的输出数据是一个区域内的二维点集，每个时刻 $t$ 的坐标是 $(x^t_i,y^t_i)$，对应值是 $(u^t_i, v^t_i, p^t_i)$，因此我们只需要将评估的输出数据按时刻保存成 16 个 **vtu格式** 文件，最后用可视化软件打开查看即可。代码如下： -``` py linenums="155" +``` py linenums="164" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:155:186 +examples/ldc/ldc2d_unsteady_Re10.py:164:195 --8<-- ``` @@ -340,9 +339,9 @@ examples/ldc/ldc2d_unsteady_Re10.py:155:186 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估、可视化。 -``` py linenums="188" +``` py linenums="197" --8<-- -examples/ldc/ldc2d_unsteady_Re10.py:188:209 +examples/ldc/ldc2d_unsteady_Re10.py:197: --8<-- ``` diff --git a/docs/zh/examples/lorenz.md b/docs/zh/examples/lorenz.md index 153e9c13c..1ed345592 100644 --- a/docs/zh/examples/lorenz.md +++ b/docs/zh/examples/lorenz.md @@ -259,7 +259,7 @@ examples/lorenz/train_transformer.py:170:188 首先使用上文中的 `mse_validator` 中的数据集进行可视化，另外还引入了 `vis_data_nums` 变量用于控制需要可视化样本的数量。最后通过 `VisualizerScatter3D` 构建可视化器。 -#### 3.4.6 模型训练、评估与可视化 +#### 3.4.5 模型训练、评估与可视化 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。 diff --git a/docs/zh/examples/rossler.md b/docs/zh/examples/rossler.md index 42fbc9f56..cacf53a18 100644 --- a/docs/zh/examples/rossler.md +++ b/docs/zh/examples/rossler.md @@ -244,7 +244,7 @@ examples/rossler/train_transformer.py:167:185 首先使用上文中的 `mse_validator` 中的数据集进行可视化，另外还引入了 `vis_data_nums` 变量用于控制需要可视化样本的数量。最后通过 `VisualizerScatter3D` 构建可视化器。 -#### 3.3.6 模型训练、评估与可视化 +#### 3.3.5 模型训练、评估与可视化 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练、评估。 diff --git a/docs/zh/examples/shock_wave.md b/docs/zh/examples/shock_wave.md index c094ae938..df850ae1e 100644 --- a/docs/zh/examples/shock_wave.md +++ b/docs/zh/examples/shock_wave.md @@ -16,29 +16,28 @@ PINN-WE 模型通过损失函数加权，在 PINN 优化过程中减弱强梯度 $$ \begin{array}{cc} - \dfrac{\partial \hat{U}}{\partial t}+\dfrac{\partial \hat{F}}{\partial \xi}+\dfrac{\partial \hat{G}}{\partial \eta}=0 \\ - \text { 其中, } \quad - \begin{cases} - \hat{U}=J U \\ - \hat{F}=J\left(F \xi_x+G \xi_y\right) \\ - \hat{G}=J\left(F \eta_x+G \eta_y\right) - \end{cases} \\ - U=\left(\begin{array}{l} - \rho \\ - \rho u \\ - \rho v \\ - E - \end{array}\right), \quad F=\left(\begin{array}{l} - \rho u \\ - \rho u^2+p \\ - \rho u v \\ - (E+p) u - \end{array}\right), \quad G=\left(\begin{array}{l} - \rho v \\ - \rho v u \\ - \rho v^2+p \\ - (E+p) v - \end{array}\right) +\dfrac{\partial \hat{U}}{\partial t}+\dfrac{\partial \hat{F}}{\partial \xi}+\dfrac{\partial \hat{G}}{\partial \eta}=0 \\ +\text { 其中, } \quad\left\{\begin{array}{l} +\hat{U}=J U \\ +\hat{F}=J\left(F \xi_x+G \xi_y\right) \\ +\hat{G}=J\left(F \eta_x+G \eta_y\right) +\end{array}\right. \\ +U=\left(\begin{array}{l} +\rho \\ +\rho u \\ +\rho v \\ +\rho E +\end{array}\right), \quad F=\left(\begin{array}{l} +\rho u \\ +\rho u^2+p \\ +\rho u v \\ +(\rho E+p) u +\end{array}\right), \quad G=\left(\begin{array}{l} +\rho v \\ +\rho v u \\ +\rho v^2+p \\ +(\rho E+p) v +\end{array}\right) \end{array} $$ @@ -229,43 +228,25 @@ examples/shock_wave/shock_wave.py:433:504 ## 4. 完整代码 -=== "Ma=2.0" - - ``` py linenums="1" title="shock_wave.py" - --8<-- - examples/shock_wave/shock_wave.py - --8<-- - ``` - -=== "Ma=0.728" - - ``` py linenums="1" title="shock_wave.py" - --8<-- - examples/shock_wave/shock_wave.py::243 - --8<-- - MA=0.728 - --8<-- - examples/shock_wave/shock_wave.py:246: - --8<-- - ``` +``` py linenums="1" title="shock_wave.py" +--8<-- +examples/shock_wave/shock_wave.py +--8<-- +``` ## 5. 结果展示 本案例针对 $Ma=2.0$ 和 $Ma=0.728$ 两种不同的参数配置进行了实验，结果如下所示 -=== "Ma=2.0" - -
- ![Ma_2.0](https://paddle-org.bj.bcebos.com/paddlescience/docs/ShockWave/shock_wave(Ma_2.000).png){ loading=lazy } -
Ma=2.0时，x方向速度u、y方向速度v、压力p、密度rho的预测结果
-
- -=== "Ma=0.728" +
+ ![Ma_2.0](https://paddle-org.bj.bcebos.com/paddlescience/docs/ShockWave/shock_wave(Ma_2.000).png){ loading=lazy } +
Ma=2.0时，x方向速度u、y方向速度v、压力p、密度rho的预测结果
+
-
- ![Ma_0.728](https://paddle-org.bj.bcebos.com/paddlescience/docs/ShockWave/shock_wave(Ma_0.728).png){ loading=lazy } -
Ma=0.728时，x方向速度u、y方向速度v、压力p、密度rho的预测结果
-
+
+ ![Ma_0.728](https://paddle-org.bj.bcebos.com/paddlescience/docs/ShockWave/shock_wave(Ma_0.728).png){ loading=lazy } +
Ma=0.728时，x方向速度u、y方向速度v、压力p、密度rho的预测结果
+
## 6. 参考资料 diff --git a/docs/zh/examples/tempoGAN.md b/docs/zh/examples/tempoGAN.md index 8d8151c10..ffa69b5cf 100644 --- a/docs/zh/examples/tempoGAN.md +++ b/docs/zh/examples/tempoGAN.md @@ -2,30 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat -O datasets/tempoGAN/2d_train.mat - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat -O datasets/tempoGAN/2d_valid.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat --output datasets/tempoGAN/2d_train.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat --output datasets/tempoGAN/2d_valid.mat - python tempoGAN.py - ``` - -=== "模型评估命令" - - ``` sh - # linux - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat -O datasets/tempoGAN/2d_train.mat - wget https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat -O datasets/tempoGAN/2d_valid.mat - # windows - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat --output datasets/tempoGAN/2d_train.mat - # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat --output datasets/tempoGAN/2d_valid.mat - python tempoGAN.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/tempogan/tempogan_pretrained.pdparams - ``` - ## 1. 背景简介 流体模拟方面的问题，捕捉湍流的复杂细节一直是数值模拟的长期挑战，用离散模型解决这些细节会产生巨大的计算成本，对于人类空间和时间尺度上的流动来说，很快就会变得不可行。因此流体超分辨率的需求应运而生，它旨在通过流体动力学模拟和深度学习技术将低分辨率流体模拟结果恢复为高分辨率结果，以减少生成高分辨率流体过程中的巨大计算成本。该技术可以应用于各种流体模拟，例如水流、空气流动、火焰模拟等。 @@ -51,9 +27,9 @@ GAN 网络为无监督学习，本问题网络设计中将目标值作为一个 运行本问题代码前请下载 [训练数据集](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_train.mat) 和 [验证数据集](https://paddle-org.bj.bcebos.com/paddlescience/datasets/tempoGAN/2d_valid.mat)， 下载后分别存放在路径： -``` yaml linenums="26" +``` py linenums="36" --8<-- -examples/tempoGAN/conf/tempogan.yaml:26:27 +examples/tempoGAN/tempoGAN.py:36:37 --8<-- ``` @@ -78,9 +54,9 @@ examples/tempoGAN/conf/tempogan.yaml:26:27 由于 GAN 网络中生成器和判别器的中间结果要相互调用，参与对方的 loss 计算，因此使用 Model List 实现，用 PaddleScience 代码表示如下： -``` py linenums="51" +``` py linenums="63" --8<-- -examples/tempoGAN/tempoGAN.py:51:70 +examples/tempoGAN/tempoGAN.py:63:152 --8<-- ``` @@ -120,9 +96,9 @@ examples/tempoGAN/functions.py:368:368 我们需要指定问题相关的参数，如数据集路径、各项 loss 的权重参数等。 -``` yaml linenums="26" +``` py linenums="34" --8<-- -examples/tempoGAN/conf/tempogan.yaml:26:36 +examples/tempoGAN/tempoGAN.py:34:61 --8<-- ``` @@ -130,9 +106,9 @@ examples/tempoGAN/conf/tempogan.yaml:26:36 同时需要指定训练轮数和学习率等超参数，注意由于 GAN 网络训练流程与一般单个模型的网络不同，`EPOCHS` 的设置也有所不同。 -``` yaml linenums="30" +``` py linenums="154" --8<-- -examples/tempoGAN/conf/tempogan.yaml:30:32 +examples/tempoGAN/tempoGAN.py:154:158 --8<-- ``` @@ -140,9 +116,9 @@ examples/tempoGAN/conf/tempogan.yaml:30:32 训练使用 Adam 优化器，学习率在 `Epoch` 达到一半时减小到原来的 $1/20$，因此使用 `Step` 方法作为学习率策略。如果将 `by_epoch` 设为 True，学习率将根据训练的 `Epoch` 改变，否则将根据 `Iteration` 改变。 -``` py linenums="72" +``` py linenums="160" --8<-- -examples/tempoGAN/tempoGAN.py:72:88 +examples/tempoGAN/tempoGAN.py:160:181 --8<-- ``` @@ -150,9 +126,9 @@ examples/tempoGAN/tempoGAN.py:72:88 本问题采用无监督学习的方式，虽然不是以监督学习方式进行训练，但此处仍然可以采用监督约束 `SupervisedConstraint`，在定义约束之前，需要给监督约束指定文件路径等数据读取配置，因为数据集中没有标签数据，因此在数据读取时我们需要使用训练数据充当标签数据，并注意在之后不要使用这部分“假的”标签数据。 -``` py linenums="94" +``` py linenums="187" --8<-- -examples/tempoGAN/tempoGAN.py:94:108 +examples/tempoGAN/tempoGAN.py:187:201 --8<-- ``` @@ -162,9 +138,9 @@ examples/tempoGAN/tempoGAN.py:94:108 下面是约束的具体内容，要注意上述提到的给定“假的”标签数据： -``` py linenums="92" +``` py linenums="183" --8<-- -examples/tempoGAN/tempoGAN.py:92:118 +examples/tempoGAN/tempoGAN.py:183:211 --8<-- ``` @@ -189,17 +165,17 @@ examples/tempoGAN/tempoGAN.py:92:118 在约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问，由于本问题设置了`use_spatialdisc` 和 `use_tempodisc`，导致 Generator 的部分约束不一定存在，因此先封装一定存在的约束到字典中，当其余约束存在时，在向字典中添加约束元素。 -``` py linenums="120" +``` py linenums="213" --8<-- -examples/tempoGAN/tempoGAN.py:120:148 +examples/tempoGAN/tempoGAN.py:213:241 --8<-- ``` #### 3.6.2 Discriminator 的约束 -``` py linenums="153" +``` py linenums="243" --8<-- -examples/tempoGAN/tempoGAN.py:153:191 +examples/tempoGAN/tempoGAN.py:243:284 --8<-- ``` @@ -207,9 +183,9 @@ examples/tempoGAN/tempoGAN.py:153:191 #### 3.6.3 Discriminator_tempo 的约束 -``` py linenums="196" +``` py linenums="286" --8<-- -examples/tempoGAN/tempoGAN.py:196:234 +examples/tempoGAN/tempoGAN.py:286:327 --8<-- ``` @@ -225,9 +201,9 @@ examples/tempoGAN/functions.py:153:229 --8<-- ``` -``` py linenums="300" +``` py linenums="372" --8<-- -examples/tempoGAN/tempoGAN.py:300:315 +examples/tempoGAN/tempoGAN.py:372:376 --8<-- ``` @@ -271,7 +247,7 @@ examples/tempoGAN/functions.py:411:427 ``` py linenums="430" --8<-- -examples/tempoGAN/functions.py:430:488 +examples/tempoGAN/functions.py:430:481 --8<-- ``` @@ -281,9 +257,9 @@ examples/tempoGAN/functions.py:430:488 完成上述设置之后，首先需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练。 -``` py linenums="237" +``` py linenums="329" --8<-- -examples/tempoGAN/tempoGAN.py:237:248 +examples/tempoGAN/tempoGAN.py:329:367 --8<-- ``` @@ -293,9 +269,9 @@ examples/tempoGAN/tempoGAN.py:237:248 由于本问题的输出为图片，评估指标需要使用针对图片的评估指标，因此不使用 PaddleScience 中内置的评估器，也不在训练过程中进行评估，而是在训练结束后针对最后一个 `Epoch` 进行一次评估: -``` py linenums="277" +``` py linenums="390" --8<-- -examples/tempoGAN/tempoGAN.py:277:284 +examples/tempoGAN/tempoGAN.py:390:402 --8<-- ``` diff --git a/docs/zh/examples/volterra_ide.md b/docs/zh/examples/volterra_ide.md index c64979b34..6b32981a1 100644 --- a/docs/zh/examples/volterra_ide.md +++ b/docs/zh/examples/volterra_ide.md @@ -2,22 +2,6 @@ AI Studio快速体验 -=== "模型训练命令" - - ``` sh - python volterra_ide.py - ``` - -=== "模型评估命令" - - ``` sh - python volterra_ide.py mode=eval EVAL.pretrained_model_path=https://paddle-org.bj.bcebos.com/paddlescience/models/volterra_ide/volterra_ide_pretrained.pdparams - ``` - -| 预训练模型 | 指标 | -|:--| :--| -| [volterra_ide_pretrained.pdparams](https://paddle-org.bj.bcebos.com/paddlescience/models/volterra_ide/volterra_ide_pretrained.pdparams) | loss(L2Rel_Validator): 0.00023
L2Rel.u(L2Rel_Validator): 0.00023 | - ## 1. 背景简介 Volterra integral equation(沃尔泰拉积分方程)是一种积分方程，即方程中含有对待求解函数的积分运算，其有两种形式，如下所示 @@ -61,9 +45,9 @@ $$ 在上述问题中，我们确定了输入为 $x$，输出为 $u(x)$，因此我们使用，用 PaddleScience 代码表示如下： -``` py linenums="39" +``` py linenums="37" --8<-- -examples/ide/volterra_ide.py:39:40 +examples/ide/volterra_ide.py:37:38 --8<-- ``` @@ -73,9 +57,9 @@ examples/ide/volterra_ide.py:39:40 Volterra_IDE 问题的积分域是 $a$ ~ $t$，其中 `a` 为固定常数 0，`t` 的范围为 0 ~ 5，因此可以使用PaddleScience 内置的一维几何 `TimeDomain` 作为计算域。 -``` py linenums="42" +``` py linenums="40" --8<-- -examples/ide/volterra_ide.py:42:43 +examples/ide/volterra_ide.py:40:42 --8<-- ``` @@ -83,9 +67,9 @@ examples/ide/volterra_ide.py:42:43 由于 Volterra_IDE 使用的是积分方程，因此可以直接使用 PaddleScience 内置的 `ppsci.equation.Volterra`，并指定所需的参数：积分下限 `a`、`t` 的离散取值点数 `num_points`、一维高斯积分点的个数 `quad_deg`、$K(t,s)$ 核函数 `kernel_func`、$u(t) - f(t)$ 等式右侧表达式 `func`。 -``` py linenums="45" +``` py linenums="44" --8<-- -examples/ide/volterra_ide.py:45:61 +examples/ide/volterra_ide.py:44:64 --8<-- ``` @@ -97,9 +81,9 @@ examples/ide/volterra_ide.py:45:61 由于等式左侧涉及到积分计算（实际采用高斯积分近似计算），因此在 0 ~ 5 区间内采样出多个 `t_i` 点后，还需要计算其用于高斯积分的点集，即对每一个 `(0,t_i)` 区间，都计算出一一对应的高斯积分点集 `quad_i` 和点权 `weight_i`。PaddleScience 将这一步作为输入数据的预处理，加入到代码中，如下所示 -``` py linenums="63" +``` py linenums="66" --8<-- -examples/ide/volterra_ide.py:63:117 +examples/ide/volterra_ide.py:66:108 --8<-- ``` @@ -113,17 +97,17 @@ $$ 因此可以加入 `t=0` 时的初值条件，代码如下所示 -``` py linenums="119" +``` py linenums="110" --8<-- -examples/ide/volterra_ide.py:119:137 +examples/ide/volterra_ide.py:110:128 --8<-- ``` 在微分方程约束、初值约束构建完毕之后，以我们刚才的命名为关键字，封装到一个字典中，方便后续访问。 -``` py linenums="138" +``` py linenums="129" --8<-- -examples/ide/volterra_ide.py:138:142 +examples/ide/volterra_ide.py:129:133 --8<-- ``` @@ -131,9 +115,9 @@ examples/ide/volterra_ide.py:138:142 接下来我们需要指定训练轮数和学习率，此处我们按实验经验，让 `L-BFGS` 优化器进行一轮优化即可，但一轮优化内的 `max_iters` 数可以设置为一个较大的一个数 `15000`。 -``` yaml linenums="39" +``` py linenums="135" --8<-- -examples/ide/conf/volterra_ide.yaml:39:57 +examples/ide/volterra_ide.py:135:136 --8<-- ``` @@ -141,9 +125,9 @@ examples/ide/conf/volterra_ide.yaml:39:57 训练过程会调用优化器来更新模型参数，此处选择较为常用的 `LBFGS` 优化器。 -``` py linenums="144" +``` py linenums="138" --8<-- -examples/ide/volterra_ide.py:144:145 +examples/ide/volterra_ide.py:138:146 --8<-- ``` @@ -151,9 +135,9 @@ examples/ide/volterra_ide.py:144:145 在训练过程中通常会按一定轮数间隔，用验证集（测试集）评估当前模型的训练情况，因此使用 `ppsci.validate.GeometryValidator` 构建评估器。 -``` py linenums="147" +``` py linenums="148" --8<-- -examples/ide/volterra_ide.py:147:161 +examples/ide/volterra_ide.py:148:163 --8<-- ``` @@ -165,9 +149,9 @@ examples/ide/volterra_ide.py:147:161 完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练。 -``` py linenums="163" +``` py linenums="165" --8<-- -examples/ide/volterra_ide.py:163:181 +examples/ide/volterra_ide.py:165:181 --8<-- ``` @@ -177,7 +161,7 @@ examples/ide/volterra_ide.py:163:181 ``` py linenums="183" --8<-- -examples/ide/volterra_ide.py:183:194 +examples/ide/volterra_ide.py:183: --8<-- ``` diff --git a/docs/zh/overview.md b/docs/zh/overview.md index 4be3cf7be..a3c1a4669 100644 --- a/docs/zh/overview.md +++ b/docs/zh/overview.md @@ -2,8 +2,6 @@ PaddleScience 在代码结构上划分为 12 个模块。从一般深度学习工作流的角度来看，这 12 个模块分别负责构建输入数据、构建神经网络模型、构建损失函数、构建优化器，训练、评估、可视化等功能。从科学计算角度来看，部分模块承担了不同于 CV、NLP 任务的功能，比如用于物理机理驱动的 Equation 模块，定义方程公式和辅助高阶微分计算；用于涉及几何场景采样的 Geometry 模块，定义简单、复杂几何形状并在其内部、边界采样构造数据；Constraint 模块将不同的优化目标视为一种“约束”，使得套件能用一套训练代码统一物理机理驱动、数据驱动、数理融合三种不同的求解流程。 -![panorama](https://paddle-org.bj.bcebos.com/paddlescience/docs/overview/panorama.png) - ## 1. 整体工作流
@@ -48,13 +46,19 @@ AutoDiff 模块负责计算高阶微分功能，内置基于 Paddle 自动微分 ### 2.4 Data -Data 模块负责数据的读取、包装和预处理，如下所示。 +Data 模块负责数据的读取、包装和预处理，由以下 3 个子模块分别负责。 + +#### 2.4.1 [Dataset](./api/data/dataset.md) + +Dataset 模块存放各种数据集的包装类，将数据包装成统一的结构再用于读取。 + +#### 2.4.2 [Transform](./api/data/process/transform.md) + +Transform 模块存放各种基于单样本的数据预处理方法，包括数据平移 `Translate` 和数据缩放 `Scale`，一般与 `data.dataset` 结合使用。 -| 子模块名称 | 子模块功能 | -| :-- | :-- | -| [ppsci.data.dataset](./api/data/dataset.md)| 数据集相关 | -| [ppsci.data.transform](./api/data/process/transform.md)| 单个数据样本预处理相关方法 | -| [ppsci.data.batch_transform](./api/data/process/batch_transform.md)| 批数据预处理相关方法 | +#### 2.4.3 [BatchTransform](./api/data/process/batch_transform.md) + +BatchTransform 模块存放各种基于批样本的数据预处理方法。 ### 2.5 [Equation](./api/equation.md) @@ -78,35 +82,17 @@ Loss 模块负责定义各种损失函数，在模型前向与方程计算完毕 同时该模块也提供了常见的多任务学习优化功能，包括 PCGrad、AGDA，进一步提升多个 loss 共同优化（如 PINN 方法）的精度。 -### 2.8 Optimizer - -Optimizer 模块包含 [`ppsci.optimizer.optimizer`](./api/optimizer.md) 与 [`ppsci.optimizer.lr_scheduler`](./api/lr_scheduler.md) 两个子模块，如下所示。 +### 2.8 [Optimizer](./api/optimizer.md) -| 子模块名称 | 子模块功能 | -| :-- | :-- | -| [ppsci.utils.optimizer](./api/optimizer.md)| 优化器相关 | -| [ppsci.utils.lr_scheduler](./api/lr_scheduler.md)| 学习率调节器相关 | +Optimizer 模块负责定义各种优化器，如 `SGD`、`Adam`、`LBFGS`。 ### 2.9 [Solver](./api/solver.md) Solver 模块负责定义求解器，作为训练、评估、推理、可视化的启动和管理引擎。 -### 2.10 Utils - -Utils 模块内部存放了一些适用于多种场景下的工具类、函数，例如在 `reader.py` 下的数据读取函数，在 `logger.py` 下的日志打印函数，以及在 `expression.py` 下的方程计算类。 - -根据其功能细分为以下 8 个子模块 +### 2.10 [Utils](./api/utils.md) -| 子模块名称 | 子模块功能 | -| :-- | :-- | -| [ppsci.utils.checker](./api/utils/checker.md)| ppsci 安装功能检查相关 | -| [ppsci.utils.expression](./api/utils/expression.md)| 负责训练、评估、可视化过程中涉及模型、方程的前向计算 | -| [ppsci.utils.initializer](./api/utils/initializer.md)| 常用参数初始化方法 | -| [ppsci.utils.logger](./api/utils/logger.md)| 日志打印模块 | -| [ppsci.utils.misc](./api/utils/misc.md)| 存放通用函数 | -| [ppsci.utils.reader](./api/utils/reader.md)| 文件读取模块 | -| [ppsci.utils.save_load](./api/utils/save_load.md)| 模型参数保存与加载 | -| [ppsci.utils.symbolic](./api/utils/symbolic.md)| sympy 符号计算功能相关 | +Utils 模块内部存放了一些适用于多种场景下的工具类、函数，如在 `reader.py` 下的数据读取函数，在 `logger.py` 下的日志打印函数，以及在 `expression.py` 下的方程计算类。 ### 2.11 [Validate](./api/validate.md) diff --git a/docs/zh/reproduction.md b/docs/zh/reproduction.md index fead4aa6a..da5f62d6c 100644 --- a/docs/zh/reproduction.md +++ b/docs/zh/reproduction.md @@ -10,11 +10,11 @@ ### 1.2 飞桨与 PaddleScience -**除特殊说明外，模型复现默认要求基于 PaddleScience** +**模型复现要求基于 PaddlePaddle 或 PaddleScience** **PaddleScience** -基于飞桨的 AI4S 套件，提供面向 AI4S 领域通用功能，如复杂几何形状解析、通用微分方程、数据驱动/物理机理/数理融合等求解器，方便开发 AI4S 领域相关模型，具体参考 [PaddleScience 文档](https://paddlescience-docs.readthedocs.io/zh/latest/) +基于飞桨的AI4S套件，提供面向 AI4S 领域通用功能，如复杂几何形状解析、通用微分方程、数据驱动/物理机理/数理融合等求解器，方便开发 AI4S 领域相关模型，具体参考 [PaddleScience 文档](https://paddlescience-docs.readthedocs.io/zh/latest/) **飞桨PaddlePaddle** @@ -22,7 +22,7 @@ ## 2. 复现步骤 -优先基于 PaddleScience 复现，如复现代码的实现逻辑和 PaddleScience 存在严重冲突，可考虑使用 PaddlePaddle API 复现。 +优先基于 PaddleScience 复现，如复现代码的实现逻辑和 PaddleSciecne 存在严重冲突，可考虑使用 PaddlePaddle 框架复现。 ![reproduce process](../images/overview/reproduction_process.png) @@ -34,22 +34,22 @@ 初步对照基准论文中提供的结果，评估提供的代码是否完整、可执行，具体为： - * 若有问题，则需要与飞桨团队反馈论文问题，由飞桨团队评估论文/模型复现的必要性，若该论文/模型价值较高，且具备了复现的条件后，则可重新进入复现流程； + * 若有问题，则需要与飞桨团队反馈论文问题，由飞桨团队评估论文/模型复现的必要性，若该论文/模型价值高，且具备了复现的条件后，则可重新进入复现流程； * 若无问题，则正式进入论文/模型的复现阶段 2. 背景说明 - 结合给定的论文，需解释论文描述的领域问题（eg. 流体、材料等）、介绍自己的复现/开发工作，即对基准论文中摘要、简介有完整的介绍（开放课题则描述该课题的背景），之后对论文的方法，应用的模型进行说明。 + 结合给定的论文，需解释论文描述的领域问题（eg.流体、材料等）、介绍自己的复现/开发工作，即对基准论文中摘要、简介有个完整的介绍（开放课题则描述该课题的背景），之后对论文的方法，应用的模型进行说明。 3. 方法与模型 - 解释基准论文所用到的理论、方法以及所用网络模型的原理等，即对论文的核心技术部分进行说明，同时说明论文中该方法、模型所体现的价值（或相对于传统求解方法的优势等）。 + 解释基准论文所用到的理论、方法以及所用网络模型的原理等，即对论文的核心技术部分进行说明，同时说明论文中该方法、模型所体现的价值（或相对于传统求解方法的优势等） 4. 训练与验证 - 对基准论文中提供的典型案例，整体说明案例的原理（eg. 流体 N-S 方程求解）、说明训练的过程（如数据集来源、内容，超参数设定，硬件环境及训练时间等）。 + 对基准论文中提供的典型案例，整体说明案例的原理（eg. 流体 N-S 方程求解）、说明训练的过程（如数据集来源、内容，超参数设定，硬件环境及训练时间等） -### 2.2 基于 PaddleScience 的代码复现 +### 2.2 基于PaddleScience的代码复现 1. 如果源代码使用 pytorch 实现，可优先使用 [PaConvert](https://github.com/PaddlePaddle/PaConvert#%E6%9C%80%E8%BF%91%E6%9B%B4%E6%96%B0) 一键自动转换 pytorch 代码为 paddle 代码，配合 [PaDiff](https://github.com/PaddlePaddle/PaDiff#%E7%AE%80%E4%BB%8B) 验证转换前后模型的精度对齐情况；如果源代码使用非 pytorch 实现（如 tensorflow），则需要列出需要基于飞桨复现的 API，同时需要形成 API 映射表，基于该映射表手动转换 tensorflow API 为 paddle API，若飞桨缺少对应的API可着重说明。 @@ -63,7 +63,7 @@ 4. 复现论文中指标结果 - 结合论文中提到的典型 demo，进行关键指标复现，即能够基于飞桨复现论文中的指标，如图表、数据等，其收敛趋势、数值等应基本一致（与作者提供指标的相对误差在 ±10% 以内即可） + 结合论文中提到的典型 demo，进行关键指标复现，即能够基于飞桨复现论文中的指标，如图表、数据等，其收敛趋势、数值等应完全一致（文中 demo 指标的相对误差在 ±10% 以内即可） 5. 代码合入，完成复现 @@ -74,7 +74,7 @@ ### 3.1 交付产物列表 | 产物 | 具体内容 | -| ----- | ---- | +| -------- | -------------------------------------------------------------------------------------------------------------------------------------- | | 模型 | 基于 PaddleScience 复现的代码、模型预训练参数 | | 文档 | AIStudio 文档、PaddleScience 文档 | @@ -89,109 +89,109 @@ 整体代码规范遵循 PEP8 [https://peps.python.org/pep-0008/](https://peps.python.org/pep-0008/) ，除此之外需要注意： -* 文件和文件夹命名中，尽量使用下划线 `_` 代表空格，不要使用 `-`。 -* 模型定义过程中，需要有一个统一的变量（parameter）命名管理手段，如尽量手动声明每个变量的名字并支持名称可变，禁止将名称定义为一个常数（如 "embedding"），避免在复用代码阶段出现各种诡异的问题。 -* 重要文件，变量的名称定义过程中需要能够通过名字表明含义，禁止使用含混不清的名称，如 net.py, aaa.py 等。 -* 在代码中定义文件(夹)路径时，需要使用 `os.path.join` 完成，禁止使用 `string` 相加的方式，这会导致模型对 `windows` 环境缺乏支持。 +* 文件和文件夹命名中，尽量使用下划线 `_` 代表空格，不要使用 `-` +* 模型定义过程中，需要有一个统一的变量（parameter）命名管理手段，如尽量手动声明每个变量的名字并支持名称可变，禁止将名称定义为一个常数（如 "embedding"），避免在复用代码阶段出现各种诡异的问题 +* 重要文件，变量的名称定义过程中需要能够通过名字表明含义，禁止使用含混不清的名称，如 net.py, aaa.py 等 +* 在代码中定义文件(夹)路径时，需要使用 `os.path.join` 完成，禁止使用 `string` 相加的方式，这会导致模型对 `windows` 环境缺乏支持 * 对于代码中重要的部分，需要加入注释介绍功能，帮助用户快速熟悉代码结构，包括但不仅限于： * Dataset、DataLoader的定义。 - * 整个模型定义，包括input，运算过程，loss等内容。 - * init，save，load，等io部分。 - * 运行中间的关键状态，如print loss，save model等。 -* 一个比较符合代码规范的例子如下。 + * 整个模型定义，包括input，运算过程，loss等内容 + * init，save，load，等io部分 + * 运行中间的关键状态，如print loss，save model等 +* 一个比较符合代码规范的例子如下： - ``` py - from paddle import io - from paddle.vision import transforms as T - from PIL import Image - import numpy as np +``` py +from paddle import io +from paddle.vision import transforms as T +from PIL import Image +import numpy as np - IMAGE_SIZE = 256 +IMAGE_SIZE = 256 - class PetDataset(io.Dataset): +class PetDataset(io.Dataset): + """ + Pet 数据集定义 + """ + + def __init__(self, mode="train"): """ - Pet 数据集定义 + 构造函数 """ - - def __init__(self, mode="train"): - """ - 构造函数 - """ - if mode not in ["train", "test", "predict"]: - raise ValueError( - f"mode should be 'train' or 'test' or 'predict', but got {mode}" - ) - self.image_size = IMAGE_SIZE - self.mode = mode - self.train_images = [] - self.label_images = [] - with open(f"./{self.mode}.txt", "r") as f: - for line in f.readlines(): - image, label = line.strip().split("\t") - self.train_images.append(image) - self.label_images.append(label) - - def _load_img(self, path, color_mode="rgb", transforms=[]): - """ - 统一的图像处理接口封装，用于规整图像大小和通道 - """ - img = Image.open(path) - if color_mode == "grayscale": - # if image is not already an 8-bit, 16-bit or 32-bit grayscale image - # convert it to an 8-bit grayscale image. - if img.mode not in ("L", "I;16", "I"): - img = img.convert("L") - elif color_mode == "rgba": - if img.mode != "RGBA": - img = img.convert("RGBA") - elif color_mode == "rgb": - if img.mode != "RGB": - img = img.convert("RGB") - else: - raise ValueError( - f"color_mode should be 'grayscale', 'rgb', or 'rgba', but got {color_mode}" - ) - return T.Compose([T.Resize(self.image_size)] + transforms)(img) - - def __getitem__(self, idx): - """ - 返回 image, label - """ - train_image = self._load_img( - self.train_images[idx], - transforms=[T.Transpose(), T.Normalize(mean=127.5, std=127.5)], - ) # 加载原始图像 - label_image = self._load_img( - self.label_images[idx], color_mode="grayscale", transforms=[T.Grayscale()] - ) # 加载Label图像 - # 返回image, label - train_image = np.array(train_image, dtype="float32") - label_image = np.array(label_image, dtype="int64") - return train_image, label_image - - def __len__(self): - """ - 返回数据集总数 - """ - return len(self.train_images) - ``` + if mode not in ["train", "test", "predict"]: + raise ValueError( + f"mode should be 'train' or 'test' or 'predict', but got {mode}" + ) + self.image_size = IMAGE_SIZE + self.mode = mode + self.train_images = [] + self.label_images = [] + with open(f"./{self.mode}.txt", "r") as f: + for line in f.readlines(): + image, label = line.strip().split("\t") + self.train_images.append(image) + self.label_images.append(label) + + def _load_img(self, path, color_mode="rgb", transforms=[]): + """ + 统一的图像处理接口封装，用于规整图像大小和通道 + """ + img = Image.open(path) + if color_mode == "grayscale": + # if image is not already an 8-bit, 16-bit or 32-bit grayscale image + # convert it to an 8-bit grayscale image. + if img.mode not in ("L", "I;16", "I"): + img = img.convert("L") + elif color_mode == "rgba": + if img.mode != "RGBA": + img = img.convert("RGBA") + elif color_mode == "rgb": + if img.mode != "RGB": + img = img.convert("RGB") + else: + raise ValueError( + f"color_mode should be 'grayscale', 'rgb', or 'rgba', but got {color_mode}" + ) + return T.Compose([T.Resize(self.image_size)] + transforms)(img) + + def __getitem__(self, idx): + """ + 返回 image, label + """ + train_image = self._load_img( + self.train_images[idx], + transforms=[T.Transpose(), T.Normalize(mean=127.5, std=127.5)], + ) # 加载原始图像 + label_image = self._load_img( + self.label_images[idx], color_mode="grayscale", transforms=[T.Grayscale()] + ) # 加载Label图像 + # 返回image, label + train_image = np.array(train_image, dtype="float32") + label_image = np.array(label_image, dtype="int64") + return train_image, label_image + + def __len__(self): + """ + 返回数据集总数 + """ + return len(self.train_images) +``` * 提供的代码能正常跑通训练、评估。 #### 3.2.3 文档规范 -AIStudio 文档参考：[PaddleScience-DarcyFlow - 飞桨AI Studio](https://aistudio.baidu.com/aistudio/projectdetail/6184070) +AIStudio文档参考：[PaddleScience-DarcyFlow - 飞桨AI Studio](https://aistudio.baidu.com/aistudio/projectdetail/6184070) -PaddleScience 官网文档需满足： +PaddleScience官网文档需满足： -* 复现完成后需撰写模型文档，需包含模型简介、问题定义、问题求解（逐步讲解训练评估以及可视化代码的编写过程）、完整代码、结果展示图等章节。 -* 在文档的开始，需要添加复现的论文题目、论文地址以及参考代码的链接，同时建议对参考代码的作者表示感谢。 -* 代码封装得当，易读性好，不用一些随意的变量/类/函数命名。 -* 注释清晰，不仅说明做了什么，也要说明为什么这么做。 -* 如果模型依赖 PaddlePaddle 未涵盖的依赖（如 pandas），则需要在文档开头对说明需安装哪些依赖项。 -* 随机控制，需要尽量固定含有随机因素模块的随机种子，保证模型可以正常复现（PaddleScience 套件提供了 `ppsci.utils.misc.set_random_seed(seed_num)` 语句来控制全局随机数）。 -* 超参数：模型内部超参数禁止写死，尽量都可以通过配置文件进行配置。 -* 文档末尾附上参考论文、参考代码网址、复现训练好的模型参数下载链接。 整体文档撰写可以参考：[文档参考样例(darcy2d)](https://paddlescience-docs.readthedocs.io/zh/latest/zh/examples/darcy2d/)。 +* 复现完成后需撰写模型文档，需包含模型简介、问题定义、问题求解（逐步讲解训练评估以及可视化代码的编写过程）、完整代码、结果展示图等章节 +* 在文档的开始，需要添加复现的论文题目、论文地址以及参考代码的链接，同时建议对参考代码的作者表示感谢 +* 代码封装得当，易读性好，不用一些随意的变量/类/函数命名 +* 注释清晰，不仅说明做了什么，也要说明为什么这么做 +* 如果模型依赖paddlepaddle未涵盖的依赖（如 pandas），则需要在文档开头对说明需安装哪些依赖项 +* 随机控制，需要尽量固定含有随机因素模块的随机种子，保证模型可以正常复现（PaddleScience套件提供了ppsci.utils.misc.set_random_seed(42)语句来控制全局随机数） +* 超参数：模型内部超参数禁止写死，尽量都可以通过配置文件进行配置 +* 文档末尾附上参考论文、参考代码网址、复现训练好的模型参数下载链接。 整体文档撰写可以参考：[文档参考样例(darcy2d)](https://paddlescience-docs.readthedocs.io/zh/latest/zh/examples/darcy2d/) diff --git a/docs/zh/user_guide.md b/docs/zh/user_guide.md index 5b5676ae2..ec1149669 100644 --- a/docs/zh/user_guide.md +++ b/docs/zh/user_guide.md @@ -4,215 +4,7 @@ ## 1. 基础功能 -### 1.1 使用 YAML + hydra - -PaddleScience 推荐使用 [YAML](https://pyyaml.org/wiki/PyYAMLDocumentation) 文件控制程序训练、评估、推理等过程。其主要原理是利用 [hydra](https://hydra.cc/) 配置管理工具，从 `*.yaml` 格式的文件中解析配置参数，并传递给运行代码，以对程序运行时所使用的超参数等字段进行灵活配置，提高实验效率。本章节主要介绍 hydra 配置管理工具的基本使用方法。 - -在使用 hydra 配置运行参数前，请先执行以下命令检查是否已安装 `hydra`。 - -``` shell -pip show hydra-core -``` - -如未安装，则需执行以下命令安装 `hydra`。 - -``` shell -pip install hydra-core -``` - -#### 1.1.1 打印运行配置 - -!!! warning - - 注意本教程内的打印运行配置方法**只作为调试使用**，hydra 默认在打印完配置后会立即结束程序。因此在正常运行程序时请勿加上 `-c job` 参数。 - -以 bracket 案例为例，其正常运行命令为：`python bracket.py`。若在其运行命令末尾加上 `-c job`，则可以打印出从运行配置文件 `conf/bracket.yaml` 中解析出的配置参数，如下所示。 - -``` shell title=">>> python bracket.py {++-c job++}" -mode: train -seed: 2023 -output_dir: ${hydra:run.dir} -log_freq: 20 -NU: 0.3 -E: 100000000000.0 -... -... -EVAL: - pretrained_model_path: null - eval_during_train: true - eval_with_no_grad: true - batch_size: - sup_validator: 128 -``` - -#### 1.1.2 命令行方式配置参数 - -仍然以配置文件 `bracket.yaml` 为例，关于学习率部分的参数配置如下所示。 - -``` yaml title="bracket.yaml" -... -TRAIN: - epochs: 2000 - iters_per_epoch: 1000 - save_freq: 20 - eval_during_train: true - eval_freq: 20 - lr_scheduler: - epochs: ${TRAIN.epochs} # (1) - iters_per_epoch: ${TRAIN.iters_per_epoch} - learning_rate: 0.001 - gamma: 0.95 - decay_steps: 15000 - by_epoch: false -... -``` - -1. `${...}$` 是 omegaconf 的引用语法，可以引用配置文件中其他位置上的参数，避免同时维护多个相同语义的参数副本，其效果与 yaml 的 anchor 语法类似。 - -可以看到上述配置文件中的学习率为 `0.001`，若需修改学习率为 `0.002` 以运行新的实验，则有以下两种方式： - -- 将上述配置文件中的 `learning_rate: 0.001` 改为 `learning_rate: 0.002`，然后再运行程序。这种方式虽然简单，但在实验较多时容易造成实验混乱，因此不推荐使用。 -- 通过命令行参数的方式进行修改，如下所示。 - - ``` shell - python bracket.py {++TRAIN.lr_scheduler.learning_rate=0.002++} - ``` - - 这种方式通过命令行参数临时重载运行配置，而不会对 `bracket.yaml` 文件本身进行修改，能灵活地控制运行时的配置，保证不同实验之间互不干扰。 - -#### 1.1.3 自动化运行实验 - -如 [1.1.2 命令行方式配置参数](#112) 所述，可以通过在程序执行命令的末尾加上合适的参数来控制多组实验的运行配置，接下来以自动化执行四组实验为例，介绍如何利用 hydra 的 [multirun](https://hydra.cc/docs/1.0/tutorials/basic/running_your_app/multi-run/#internaldocs-banner) 功能，实现该目的。 - -假设这四组实验围绕随机种子 `seed` 和训练轮数 `epochs` 进行配置，组合如下： - -| 实验编号 | seed | epochs | -| :------- | :--- | :----- | -| 1 | 42 | 10 | -| 2 | 42 | 20 | -| 3 | 1024 | 10 | -| 4 | 1024 | 20 | - -执行如下命令即可按顺序自动运行这 4 组实验。 - -``` shell title=">>> python bracket.py {++-m seed=42,1024 TRAIN.epochs=10,20++}" -[HYDRA] Launching 4 jobs locally -[HYDRA] #0 : seed=42 TRAIN.epochs=10 -.... -[HYDRA] #1 : seed=42 TRAIN.epochs=20 -... -[HYDRA] #2 : seed=1024 TRAIN.epochs=10 -... -[HYDRA] #3 : seed=1024 TRAIN.epochs=20 -... -``` - -多组实验各自的参数文件、日志文件则保存在以不同参数组合为名称的子文件夹中，如下所示。 - -``` shell title=">>> tree PaddleScience/examples/bracket/outputs_bracket/" -PaddleScience/examples/bracket/outputs_bracket/ -└──2023-10-14 # (1) - └── 04-01-52 # (2) - ├── TRAIN.epochs=10,20,seed=42,1024 # multirun 总配置保存目录 - │ └── multirun.yaml # multirun 配置文件 (3) - ├── {==TRAIN.epochs=10,seed=1024==} # 实验编号3的保存目录 - │ ├── checkpoints - │ │ ├── latest.pdeqn - │ │ ├── latest.pdopt - │ │ ├── latest.pdparams - │ │ └── latest.pdstates - │ ├── train.log - │ └── visual - │ └── epoch_0 - │ └── result_u_v_w_sigmas.vtu - ├── {==TRAIN.epochs=10,seed=42==} # 实验编号1的保存目录 - │ ├── checkpoints - │ │ ├── latest.pdeqn - │ │ ├── latest.pdopt - │ │ ├── latest.pdparams - │ │ └── latest.pdstates - │ ├── train.log - │ └── visual - │ └── epoch_0 - │ └── result_u_v_w_sigmas.vtu - ├── {==TRAIN.epochs=20,seed=1024==} # 实验编号4的保存目录 - │ ├── checkpoints - │ │ ├── latest.pdeqn - │ │ ├── latest.pdopt - │ │ ├── latest.pdparams - │ │ └── latest.pdstates - │ ├── train.log - │ └── visual - │ └── epoch_0 - │ └── result_u_v_w_sigmas.vtu - └── {==TRAIN.epochs=20,seed=42==} # 实验编号2的保存目录 - ├── checkpoints - │ ├── latest.pdeqn - │ ├── latest.pdopt - │ ├── latest.pdparams - │ └── latest.pdstates - ├── train.log - └── visual - └── epoch_0 - └── result_u_v_w_sigmas.vtu -``` - -1. 该文件夹是程序运行时根据日期自动创建得到，此处表示2023年10月14日 -2. 该文件夹是程序运行时根据运行时刻(世界标准时间,UTC)自动创建得到，此处表示04点01分52秒 -3. 该文件夹是 multirun 模式下额外产生一个总配置目录，主要用于保存 multirun.yaml，其内的 `hydra.overrides.task` 字段记录了用于组合出不同运行参数的原始配置。 - -考虑到用户的阅读和学习成本，本章节只介绍了常用的实验方法，更多进阶用法请参考 [hydra官方教程](https://hydra.cc/docs/tutorials/basic/your_first_app/simple_cli/)。 - -### 1.2 模型推理预测 - -若需使用训练完毕保存或下载得到的模型文件 `*.pdprams` 直接进行推理（预测），可以参考以下代码示例。 - -1. 加载 `*.pdparams` 文件内的参数到模型中 - - ``` py - import ppsci - import numpy as np - - # 实例化一个输入为 (x,y,z) 三个维度上的坐标，输出为 (u,v,w) 三个维度上的速度的 model - model = ppsci.arch.MLP(("x", "y", "z"), ("u", "v", "w"), 5, 64, "tanh") - - # 用该模型及其对应的预训练模型路径(或下载地址 url)两个参数初始化 solver - solver = ppsci.solver.Solver( - model=model, - pretrained_model_path="/path/to/pretrain.pdparams", - ) - # 在 Solver(...) 中会自动从给定的 pretrained_model_path 加载(下载)参数并赋值给 model 的对应参数 - ``` - -2. 准备好用于预测的输入数据，并以字典 `dict` 的方式传递给 `solver.predict`。 - - ``` py - N = 100 # 假设要预测100个样本的结果 - x = np.random.randn(N, 1) # 准备 字段 - y = np.random.randn(N, 1) - z = np.random.randn(N, 1) - - input_dict = { - "x": x, - "y": y, - "z": z, - } - - output_dict = solver.predict( - input_dict, - batch_size=32, # 推理时的 batch_size - return_numpy=True, # 返回结果是否转换为 numpy - ) - - # output_dict 预测结果同样以字典的形式保存在 output_dict 中，其具体内容如下 - for k, v in output_dict.items(): - print(f"{k} {v.shape}") - # "u": (100, 1) - # "v": (100, 1) - # "w": (100, 1) - ``` - -### 1.3 断点继续训练 +### 1.1 断点继续训练 在模型的日常训练中，可能存在机器故障或者用户手动操作而中断训练的情况，针对这种情况 PaddleScience 提供了断点继续训练的功能，即在训练时默认会保存**最近一个训练完毕的 epoch** 对应的各种参数到以下 5 个文件中： @@ -227,19 +19,21 @@ PaddleScience/examples/bracket/outputs_bracket/ ``` py hl_lines="9" import ppsci +... ... solver = ppsci.solver.Solver( + ..., ..., checkpoint_path="/path/to/latest" ) ``` -!!! Warning "路径填写注意事项" +???+ Warning "路径填写注意事项" 此处只需将路径填写到 "latest" 为止即可，不需要加上其后缀，程序会根据 "/path/to/latest"，自动补充不同文件对应的后缀名来加载 `latest.pdparams`、`latest.pdopt` 等文件。 -### 1.4 迁移学习 +### 1.2 迁移学习 迁移学习是一种广泛使用、低成本提高模型精度的训练方式。在 PaddleScience 中，只需在 `model` 实例化完毕之后，手动为其载入预训练模型权重，即可进行迁移学习。 @@ -255,11 +49,15 @@ model = ... save_load.load_pretrain(model, "/path/to/pretrain") ``` -!!! info "迁移学习建议" +???+ Warning "路径填写注意事项" + + 同样地，此处只需将路径填写到预训练文件的文件名为止即可，不需要加上其后缀，程序会根据 "/path/to/pretrain"，自动补充 `.pdparams` 后缀名来加载 `/path/to/pretrain.pdparams` 文件。 + +???+ info "迁移学习建议" 在迁移学习时，相对于完全随机初始化的参数而言，载入的预训练模型权重参数是一个较好的初始化状态，因此不需要使用太大的学习率，而可以将学习率适当调小 2~10 倍以获得更稳定的训练过程和更好的精度。 -### 1.5 模型评估 +### 1.3 模型评估 当模型训练完毕之后，如果想手动对某一个模型权重文件，评估其在数据集上的精度，则在 `Solver` 实例化时指定参数 `pretrained_model_path` 为该权重文件的路径，然后调用 `Solver.eval()` 即可。 @@ -278,11 +76,11 @@ solver = ppsci.solver.Solver( solver.eval() ``` -!!! Warning "路径填写注意事项" +???+ Warning "路径填写注意事项" 同样地，此处只需将路径填写到预训练权重的文件名为止即可，不需要加上其后缀，程序会根据 "/path/to/model"，自动补充所需后缀名来加载 `/path/to/model.pdparams` 文件。 -### 1.6 使用 WandB 记录实验 +### 1.4 使用 WandB 记录实验 [WandB](https://wandb.ai/) 是一个第三方实验记录工具，能在记录实验数据的同时将数据上传到其用户的私人账户上，防止实验记录丢失。 @@ -320,7 +118,7 @@ PaddleScience 支持使用 WandB 记录基本的实验数据，包括 train/eval 如上述代码所示，指定 `use_wandb=True`，并且设置 `wandb_config` 配置字典中的 `project`、`name`、`dir` 三个字段，然后启动训练即可。训练过程会实时上传记录数据至 wandb 服务器，训练结束后可以进入终端打印的预览地址在网页端查看完整训练记录曲线。 - !!! warning "注意" + ???+ warning "注意" 由于每次调用 `wandb.log` 会使得其自带的计数器 `Step` 自增 1，因此在 wandb 的网站上查看训练记录时，需要手动更改 x 轴的单位为 `step`(全小写)，如下所示。 @@ -438,6 +236,6 @@ solver = ppsci.solver.Solver( solver.train() ``` - !!! info "影响说明" + ???+ info "影响说明" 个别多任务学习方法（如weight based method）可能会改变**训练过程**中损失函数的计算方式，但仅限于影响训练过程，模型**评估过程**的损失计算方式保持不变。 diff --git a/examples/NSFNet/VP_NSFNet1.py b/examples/NSFNet/VP_NSFNet1.py new file mode 100644 index 000000000..20ca57a40 --- /dev/null +++ b/examples/NSFNet/VP_NSFNet1.py @@ -0,0 +1,333 @@ +import hydra +import numpy as np +from omegaconf import DictConfig + +import ppsci +from ppsci.utils import logger + + +def analytic_solution_generate(x, y, lam): + u = 1 - np.exp(lam * x) * np.cos(2 * np.pi * y) + v = lam / (2 * np.pi) * np.exp(lam * x) * np.sin(2 * np.pi * y) + p = 0.5 * (1 - np.exp(2 * lam * x)) + return u, v, p + + +@hydra.main(version_base=None, config_path="./conf", config_name="VP_NSFNet1.yaml") +def main(cfg: DictConfig): + if cfg.mode == "train": + train(cfg) + elif cfg.mode == "eval": + evaluate(cfg) + else: + raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") + + +def generate_data(N_TRAIN, NB_TRAIN, lam, seed): + x = np.linspace(-0.5, 1.0, 101) + y = np.linspace(-0.5, 1.5, 101) + + yb1 = np.array([-0.5] * 100) + yb2 = np.array([1] * 100) + xb1 = np.array([-0.5] * 100) + xb2 = np.array([1.5] * 100) + + y_train1 = np.concatenate([y[1:101], y[0:100], xb1, xb2], 0).astype("float32") + x_train1 = np.concatenate([yb1, yb2, x[0:100], x[1:101]], 0).astype("float32") + + xb_train = x_train1.reshape(x_train1.shape[0], 1).astype("float32") + yb_train = y_train1.reshape(y_train1.shape[0], 1).astype("float32") + ub_train, vb_train, _ = analytic_solution_generate(xb_train, yb_train, lam) + + x_train = (np.random.rand(N_TRAIN, 1) - 1 / 3) * 3 / 2 + y_train = (np.random.rand(N_TRAIN, 1) - 1 / 4) * 2 + + # generate test data + np.random.seed(seed) + x_star = ((np.random.rand(1000, 1) - 1 / 3) * 3 / 2).astype("float32") + y_star = ((np.random.rand(1000, 1) - 1 / 4) * 2).astype("float32") + + u_star, v_star, p_star = analytic_solution_generate(x_star, y_star, lam) + + return ( + x_train, + y_train, + xb_train, + yb_train, + ub_train, + vb_train, + x_star, + y_star, + u_star, + v_star, + p_star, + ) + + +def train(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + + ITERS_PER_EPOCH = cfg.iters_per_epoch + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + # set the number of boundary samples + NB_TRAIN = cfg.nb_train + + # generate data + + # set the Reynolds number and the corresponding lambda which is the parameter in the exact solution. + Re = cfg.re + lam = 0.5 * Re - np.sqrt(0.25 * (Re**2) + 4 * (np.pi**2)) + + ( + x_train, + y_train, + xb_train, + yb_train, + ub_train, + vb_train, + x_star, + y_star, + u_star, + v_star, + p_star, + ) = generate_data(N_TRAIN, NB_TRAIN, lam, SEED) + + train_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": xb_train, "y": yb_train}, + "label": {"u": ub_train, "v": vb_train}, + }, + "batch_size": NB_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star}, + "label": {"u": u_star, "v": v_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + geom = ppsci.geometry.PointCloud({"x": x_train, "y": y_train}, ("x", "y")) + + # supervised constraint s.t ||u-u_0|| + sup_constraint = ppsci.constraint.SupervisedConstraint( + train_dataloader_cfg, + ppsci.loss.MSELoss("mean"), + name="Sup", + ) + + # set equation constarint s.t. ||F(u)|| + equation = { + "NavierStokes": ppsci.equation.NavierStokes( + nu=1.0 / Re, rho=1.0, dim=2, time=False + ), + } + + pde_constraint = ppsci.constraint.InteriorConstraint( + equation["NavierStokes"].equations, + {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, + geom, + { + "dataset": {"name": "IterableNamedArrayDataset"}, + "batch_size": N_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + }, + ppsci.loss.MSELoss("mean"), + name="EQ", + ) + + constraint = { + sup_constraint.name: sup_constraint, + pde_constraint.name: pde_constraint, + } + + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + # set learning rate scheduler + epoch_list = cfg.epoch_list + new_epoch_list = [] + for i, _ in enumerate(epoch_list): + new_epoch_list.append(sum(epoch_list[: i + 1])) + EPOCHS = new_epoch_list[-1] + lr_list = cfg.lr_list + + lr_scheduler = ppsci.optimizer.lr_scheduler.Piecewise( + EPOCHS, ITERS_PER_EPOCH, new_epoch_list, lr_list + )() + + optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) + + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") + + # initialize solver + solver = ppsci.solver.Solver( + model=model, + constraint=constraint, + optimizer=optimizer, + epochs=EPOCHS, + lr_scheduler=lr_scheduler, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=False, + log_freq=cfg.log_freq, + eval_freq=cfg.eval_freq, + seed=SEED, + equation=equation, + geom=geom, + validator=validator, + visualizer=None, + eval_with_no_grad=False, + output_dir=OUTPUT_DIR, + ) + + # train model + solver.train() + + solver.eval() + + # plot the loss + solver.plot_loss_history() + + # set LBFGS optimizer + EPOCHS = 5000 + optimizer = ppsci.optimizer.LBFGS( + max_iter=50000, tolerance_change=np.finfo(float).eps, history_size=50 + )(model) + + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") + + # initialize solver + solver = ppsci.solver.Solver( + model=model, + constraint=constraint, + optimizer=optimizer, + epochs=EPOCHS, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=False, + log_freq=2000, + eval_freq=2000, + seed=SEED, + equation=equation, + geom=geom, + validator=validator, + visualizer=None, + eval_with_no_grad=False, + output_dir=OUTPUT_DIR, + ) + # train model + solver.train() + + # evaluate after finished training + solver.eval() + + +def evaluate(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + # set the Reynolds number and the corresponding lambda which is the parameter in the exact solution. + Re = cfg.re + lam = 0.5 * Re - np.sqrt(0.25 * (Re**2) + 4 * (np.pi**2)) + + x_train = (np.random.rand(N_TRAIN, 1) - 1 / 3) * 3 / 2 + y_train = (np.random.rand(N_TRAIN, 1) - 1 / 4) * 2 + + # generate test data + np.random.seed(SEED) + x_star = ((np.random.rand(1000, 1) - 1 / 3) * 3 / 2).astype("float32") + y_star = ((np.random.rand(1000, 1) - 1 / 4) * 2).astype("float32") + u_star = 1 - np.exp(lam * x_star) * np.cos(2 * np.pi * y_star) + v_star = (lam / (2 * np.pi)) * np.exp(lam * x_star) * np.sin(2 * np.pi * y_star) + p_star = 0.5 * (1 - np.exp(2 * lam * x_star)) + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star}, + "label": {"u": u_star, "v": v_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + geom = ppsci.geometry.PointCloud({"x": x_train, "y": y_train}, ("x", "y")) + + # set equation constarint s.t. ||F(u)|| + equation = { + "NavierStokes": ppsci.equation.NavierStokes( + nu=1.0 / Re, rho=1.0, dim=2, time=False + ), + } + + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + # load solver + solver = ppsci.solver.Solver( + model, + equation=equation, + geom=geom, + validator=validator, + pretrained_model_path=cfg.pretrained_model_path, ### the path of the model + ) + + # eval model + solver.eval() + + +if __name__ == "__main__": + main() diff --git a/examples/NSFNet/VP_NSFNet2.py b/examples/NSFNet/VP_NSFNet2.py new file mode 100644 index 000000000..a7d75a894 --- /dev/null +++ b/examples/NSFNet/VP_NSFNet2.py @@ -0,0 +1,491 @@ +import hydra +import matplotlib.pyplot as plt +import numpy as np +import paddle +import scipy +from omegaconf import DictConfig +from scipy.interpolate import griddata + +import ppsci +from ppsci.utils import logger + + +@hydra.main(version_base=None, config_path="./conf", config_name="VP_NSFNet2.yaml") +def main(cfg: DictConfig): + if cfg.mode == "train": + train(cfg) + elif cfg.mode == "eval": + evaluate(cfg) + else: + raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") + + +def load_data(path, N_TRAIN, NB_TRAIN, N0_TRAIN): + data = scipy.io.loadmat(path) + + U_star = data["U_star"].astype("float32") # N x 2 x T + P_star = data["p_star"].astype("float32") # N x T + t_star = data["t"].astype("float32") # T x 1 + X_star = data["X_star"].astype("float32") # N x 2 + + N = X_star.shape[0] + T = t_star.shape[0] + + # rearrange data + XX = np.tile(X_star[:, 0:1], (1, T)) # N x T + YY = np.tile(X_star[:, 1:2], (1, T)) # N x T + TT = np.tile(t_star, (1, N)).T # N x T + + UU = U_star[:, 0, :] # N x T + VV = U_star[:, 1, :] # N x T + PP = P_star # N x T + + x = XX.flatten()[:, None] # NT x 1 + y = YY.flatten()[:, None] # NT x 1 + t = TT.flatten()[:, None] # NT x 1 + + u = UU.flatten()[:, None] # NT x 1 + v = VV.flatten()[:, None] # NT x 1 + p = PP.flatten()[:, None] # NT x 1 + + data1 = np.concatenate([x, y, t, u, v, p], 1) + data2 = data1[:, :][data1[:, 2] <= 7] + data3 = data2[:, :][data2[:, 0] >= 1] + data4 = data3[:, :][data3[:, 0] <= 8] + data5 = data4[:, :][data4[:, 1] >= -2] + data_domain = data5[:, :][data5[:, 1] <= 2] + data_t0 = data_domain[:, :][data_domain[:, 2] == 0] + data_y1 = data_domain[:, :][data_domain[:, 0] == 1] + data_y8 = data_domain[:, :][data_domain[:, 0] == 8] + data_x = data_domain[:, :][data_domain[:, 1] == -2] + data_x2 = data_domain[:, :][data_domain[:, 1] == 2] + data_sup_b_train = np.concatenate([data_y1, data_y8, data_x, data_x2], 0) + idx = np.random.choice(data_domain.shape[0], N_TRAIN, replace=False) + + x_train = data_domain[idx, 0].reshape(data_domain[idx, 0].shape[0], 1) + y_train = data_domain[idx, 1].reshape(data_domain[idx, 1].shape[0], 1) + t_train = data_domain[idx, 2].reshape(data_domain[idx, 2].shape[0], 1) + + x0_train = data_t0[:, 0].reshape(data_t0[:, 0].shape[0], 1) + y0_train = data_t0[:, 1].reshape(data_t0[:, 1].shape[0], 1) + t0_train = data_t0[:, 2].reshape(data_t0[:, 2].shape[0], 1) + u0_train = data_t0[:, 3].reshape(data_t0[:, 3].shape[0], 1) + v0_train = data_t0[:, 4].reshape(data_t0[:, 4].shape[0], 1) + + xb_train = data_sup_b_train[:, 0].reshape(data_sup_b_train[:, 0].shape[0], 1) + yb_train = data_sup_b_train[:, 1].reshape(data_sup_b_train[:, 1].shape[0], 1) + tb_train = data_sup_b_train[:, 2].reshape(data_sup_b_train[:, 2].shape[0], 1) + ub_train = data_sup_b_train[:, 3].reshape(data_sup_b_train[:, 3].shape[0], 1) + vb_train = data_sup_b_train[:, 4].reshape(data_sup_b_train[:, 4].shape[0], 1) + + # set test set + snap = np.array([0]) + x_star = X_star[:, 0:1] + y_star = X_star[:, 1:2] + t_star = TT[:, snap] + + u_star = U_star[:, 0, snap] + v_star = U_star[:, 1, snap] + p_star = P_star[:, snap] + + return ( + x_train, + y_train, + t_train, + x0_train, + y0_train, + t0_train, + u0_train, + v0_train, + xb_train, + yb_train, + tb_train, + ub_train, + vb_train, + x_star, + y_star, + t_star, + u_star, + v_star, + p_star, + ) + + +def train(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + ITERS_PER_EPOCH = cfg.iters_per_epoch + + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + # set the number of boundary samples + NB_TRAIN = cfg.nb_train + + # set the number of initial samples + N0_TRAIN = cfg.n0_train + + ( + x_train, + y_train, + t_train, + x0_train, + y0_train, + t0_train, + u0_train, + v0_train, + xb_train, + yb_train, + tb_train, + ub_train, + vb_train, + x_star, + y_star, + t_star, + u_star, + v_star, + p_star, + ) = load_data(cfg.data_dir, N_TRAIN, NB_TRAIN, N0_TRAIN) + # set dataloader config + train_dataloader_cfg_b = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": xb_train, "y": yb_train, "t": tb_train}, + "label": {"u": ub_train, "v": vb_train}, + }, + "batch_size": NB_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + train_dataloader_cfg_0 = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x0_train, "y": y0_train, "t": t0_train}, + "label": {"u": u0_train, "v": v0_train}, + }, + "batch_size": N0_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star, "t": t_star}, + "label": {"u": u_star, "v": v_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + geom = ppsci.geometry.PointCloud( + {"x": x_train, "y": y_train, "t": t_train}, ("x", "y", "t") + ) + + # supervised constraint s.t ||u-u_b|| + sup_constraint_b = ppsci.constraint.SupervisedConstraint( + train_dataloader_cfg_b, + ppsci.loss.MSELoss("mean"), + name="Sup_b", + ) + + # supervised constraint s.t ||u-u_0|| + sup_constraint_0 = ppsci.constraint.SupervisedConstraint( + train_dataloader_cfg_0, + ppsci.loss.MSELoss("mean"), + name="Sup_0", + ) + + # set equation constarint s.t. ||F(u)|| + equation = { + "NavierStokes": ppsci.equation.NavierStokes( + nu=1.0 / cfg.re, rho=1.0, dim=2, time=True + ), + } + + pde_constraint = ppsci.constraint.InteriorConstraint( + equation["NavierStokes"].equations, + {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, + geom, + { + "dataset": {"name": "IterableNamedArrayDataset"}, + "batch_size": N_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + }, + ppsci.loss.MSELoss("mean"), + name="EQ", + ) + + constraint = { + pde_constraint.name: pde_constraint, + sup_constraint_b.name: sup_constraint_b, + sup_constraint_0.name: sup_constraint_0, + } + + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + # set optimizer + epoch_list = [5000, 5000, 50000, 50000] + new_epoch_list = [] + for i, _ in enumerate(epoch_list): + new_epoch_list.append(sum(epoch_list[: i + 1])) + EPOCHS = new_epoch_list[-1] + lr_list = [1e-3, 1e-4, 1e-5, 1e-6, 1e-7] + lr_scheduler = ppsci.optimizer.lr_scheduler.Piecewise( + EPOCHS, ITERS_PER_EPOCH, new_epoch_list, lr_list + )() + optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) + + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") + # initialize solver + solver = ppsci.solver.Solver( + model=model, + constraint=constraint, + optimizer=optimizer, + epochs=EPOCHS, + lr_scheduler=lr_scheduler, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=True, + log_freq=cfg.log_freq, + eval_freq=cfg.eval_freq, + seed=SEED, + equation=equation, + geom=geom, + validator=validator, + visualizer=None, + eval_with_no_grad=False, + checkpoint_path=OUTPUT_DIR + "/checkpoints/latest", + ) + # train model + solver.train() + + # evaluate after finished training + solver.eval() + + solver.plot_loss_history() + + +def evaluate(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + data = scipy.io.loadmat(cfg.data_dir) + + U_star = data["U_star"].astype("float32") # N x 2 x T + P_star = data["p_star"].astype("float32") # N x T + t_star = data["t"].astype("float32") # T x 1 + X_star = data["X_star"].astype("float32") # N x 2 + + N = X_star.shape[0] + T = t_star.shape[0] + + # rearrange data + XX = np.tile(X_star[:, 0:1], (1, T)) # N x T + YY = np.tile(X_star[:, 1:2], (1, T)) # N x T + TT = np.tile(t_star, (1, N)).T # N x T + + UU = U_star[:, 0, :] # N x T + VV = U_star[:, 1, :] # N x T + PP = P_star # N x T + + x = XX.flatten()[:, None] # NT x 1 + y = YY.flatten()[:, None] # NT x 1 + t = TT.flatten()[:, None] # NT x 1 + + u = UU.flatten()[:, None] # NT x 1 + v = VV.flatten()[:, None] # NT x 1 + p = PP.flatten()[:, None] # NT x 1 + + data1 = np.concatenate([x, y, t, u, v, p], 1) + data2 = data1[:, :][data1[:, 2] <= 7] + data3 = data2[:, :][data2[:, 0] >= 1] + data4 = data3[:, :][data3[:, 0] <= 8] + data5 = data4[:, :][data4[:, 1] >= -2] + data_domain = data5[:, :][data5[:, 1] <= 2] + + idx = np.random.choice(data_domain.shape[0], N_TRAIN, replace=False) + + x_train = data_domain[idx, 0].reshape(data_domain[idx, 0].shape[0], 1) + y_train = data_domain[idx, 1].reshape(data_domain[idx, 1].shape[0], 1) + t_train = data_domain[idx, 2].reshape(data_domain[idx, 2].shape[0], 1) + + snap = np.array([0]) + x_star = X_star[:, 0:1] + y_star = X_star[:, 1:2] + t_star = TT[:, snap] + + u_star = U_star[:, 0, snap] + v_star = U_star[:, 1, snap] + p_star = P_star[:, snap] + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star, "t": t_star}, + "label": {"u": u_star, "v": v_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + geom = ppsci.geometry.PointCloud( + {"x": x_train, "y": y_train, "t": t_train}, ("x", "y", "t") + ) + + # set equation constarint s.t. ||F(u)|| + equation = { + "NavierStokes": ppsci.equation.NavierStokes(nu=0.01, rho=1.0, dim=2, time=True), + } + + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + solver = ppsci.solver.Solver( + model, + equation=equation, + geom=geom, + validator=validator, + pretrained_model_path=cfg.pretrained_model_path, ### the path of the model + ) + + # eval + ## eval validate set + solver.eval() + + ## eval every time + us = [] + vs = [] + for i in range(0, 70): + snap = np.array([i]) + x_star = X_star[:, 0:1] + y_star = X_star[:, 1:2] + t_star = TT[:, snap] + u_star = paddle.to_tensor(U_star[:, 0, snap]) + v_star = paddle.to_tensor(U_star[:, 1, snap]) + p_star = paddle.to_tensor(P_star[:, snap]) + + solution = solver.predict({"x": x_star, "y": y_star, "t": t_star}) + u_pred = solution["u"] + v_pred = solution["v"] + p_pred = solution["p"] + p_pred = p_pred - p_pred.mean() + p_star.mean() + error_u = np.linalg.norm(u_star - u_pred, 2) / np.linalg.norm(u_star, 2) + error_v = np.linalg.norm(v_star - v_pred, 2) / np.linalg.norm(v_star, 2) + error_p = np.linalg.norm(p_star - p_pred, 2) / np.linalg.norm(p_star, 2) + us.append(error_u) + vs.append(error_v) + print("t={:.2f},relative error of u: {:.3e}".format(t_star[0].item(), error_u)) + print("t={:.2f},relative error of v: {:.3e}".format(t_star[0].item(), error_v)) + print("t={:.2f},relative error of p: {:.3e}".format(t_star[0].item(), error_p)) + + # plot + ## vorticity + grid_x, grid_y = np.mgrid[0.0:8.0:1000j, -2.0:2.0:1000j] + x_star = paddle.to_tensor(grid_x.reshape(-1, 1).astype("float32")) + y_star = paddle.to_tensor(grid_y.reshape(-1, 1).astype("float32")) + t_star = paddle.to_tensor((4.0) * np.ones(x_star.shape).astype("float32")) + x_star.stop_gradient = False + y_star.stop_gradient = False + t_star.stop_gradient = False + sol = model.forward({"x": x_star, "y": y_star, "t": t_star}) + u_y = paddle.grad(sol["u"], y_star) + v_x = paddle.grad(sol["v"], x_star) + w = np.array(u_y) - np.array(v_x) + w = w.reshape(1000, 1000) + plt.contour(grid_x, grid_y, w, levels=np.arange(-4, 5, 0.25)) + plt.savefig(f"{OUTPUT_DIR}/vorticity_t=4.png") + + ## relative error + t_snap = [] + for i in range(70): + t_snap.append(i / 10) + fig, ax = plt.subplots(1, 2, figsize=(12, 3)) + ax[0].plot(t_snap, us) + ax[1].plot(t_snap, vs) + ax[0].set_title("u") + ax[1].set_title("v") + fig.savefig(f"{OUTPUT_DIR}/l2_error.png") + + ## velocity + grid_x, grid_y = np.mgrid[0.0:8.0:1000j, -2.0:2.0:1000j] + for i in range(70): + snap = np.array([i]) + x_star = X_star[:, 0:1] + y_star = X_star[:, 1:2] + t_star = TT[:, snap] + points = np.concatenate([x_star, y_star], -1) + u_star = U_star[:, 0, snap] + v_star = U_star[:, 1, snap] + + solution = solver.predict({"x": x_star, "y": y_star, "t": t_star}) + u_pred = solution["u"] + v_pred = solution["v"] + u_star_ = griddata(points, u_star, (grid_x, grid_y), method="cubic") + u_pred_ = griddata(points, u_pred, (grid_x, grid_y), method="cubic") + v_star_ = griddata(points, v_star, (grid_x, grid_y), method="cubic") + v_pred_ = griddata(points, v_pred, (grid_x, grid_y), method="cubic") + fig, ax = plt.subplots(2, 2, figsize=(12, 8)) + ax[0, 0].contourf(grid_x, grid_y, u_star_[:, :, 0]) + ax[0, 1].contourf(grid_x, grid_y, u_pred_[:, :, 0]) + ax[1, 0].contourf(grid_x, grid_y, v_star_[:, :, 0]) + ax[1, 1].contourf(grid_x, grid_y, v_pred_[:, :, 0]) + ax[0, 0].set_title("u_exact") + ax[0, 1].set_title("u_pred") + ax[1, 0].set_title("v_exact") + ax[1, 1].set_title("v_pred") + fig.savefig(OUTPUT_DIR + f"/velocity_t={t_star[i]}.png") + + +if __name__ == "__main__": + main() diff --git a/examples/NSFNet/VP_NSFNet3.py b/examples/NSFNet/VP_NSFNet3.py new file mode 100644 index 000000000..b6b3b989f --- /dev/null +++ b/examples/NSFNet/VP_NSFNet3.py @@ -0,0 +1,529 @@ +import hydra +import matplotlib.pyplot as plt +import numpy as np +from omegaconf import DictConfig + +import ppsci +from ppsci.utils import logger + + +def analytic_solution_generate(x, y, z, t): + a, d = 1, 1 + u = ( + -a + * ( + np.exp(a * x) * np.sin(a * y + d * z) + + np.exp(a * z) * np.cos(a * x + d * y) + ) + * np.exp(-d * d * t) + ) + v = ( + -a + * ( + np.exp(a * y) * np.sin(a * z + d * x) + + np.exp(a * x) * np.cos(a * y + d * z) + ) + * np.exp(-d * d * t) + ) + w = ( + -a + * ( + np.exp(a * z) * np.sin(a * x + d * y) + + np.exp(a * y) * np.cos(a * z + d * x) + ) + * np.exp(-d * d * t) + ) + p = ( + -0.5 + * a + * a + * ( + np.exp(2 * a * x) + + np.exp(2 * a * y) + + np.exp(2 * a * z) + + 2 * np.sin(a * x + d * y) * np.cos(a * z + d * x) * np.exp(a * (y + z)) + + 2 * np.sin(a * y + d * z) * np.cos(a * x + d * y) * np.exp(a * (z + x)) + + 2 * np.sin(a * z + d * x) * np.cos(a * y + d * z) * np.exp(a * (x + y)) + ) + * np.exp(-2 * d * d * t) + ) + + return u, v, w, p + + +def generate_data(N_TRAIN, NB_TRAIN, N0_TRAIN): + # generate boundary data + x1 = np.linspace(-1, 1, 31) + y1 = np.linspace(-1, 1, 31) + z1 = np.linspace(-1, 1, 31) + t1 = np.linspace(0, 1, 11) + b0 = np.array([-1] * 900) + b1 = np.array([1] * 900) + + xt = np.tile(x1[0:30], 30) + yt = np.tile(y1[0:30], 30) + xt1 = np.tile(x1[1:31], 30) + yt1 = np.tile(y1[1:31], 30) + + yr = y1[0:30].repeat(30) + zr = z1[0:30].repeat(30) + yr1 = y1[1:31].repeat(30) + zr1 = z1[1:31].repeat(30) + + train1x = np.concatenate([b1, b0, xt1, xt, xt1, xt], 0).repeat(t1.shape[0]) + train1y = np.concatenate([yt, yt1, b1, b0, yr1, yr], 0).repeat(t1.shape[0]) + train1z = np.concatenate([zr, zr1, zr, zr1, b1, b0], 0).repeat(t1.shape[0]) + train1t = np.tile(t1, 5400) + + train1ub, train1vb, train1wb, train1pb = analytic_solution_generate( + train1x, train1y, train1z, train1t + ) + + xb_train = train1x.reshape(train1x.shape[0], 1).astype("float32") + yb_train = train1y.reshape(train1y.shape[0], 1).astype("float32") + zb_train = train1z.reshape(train1z.shape[0], 1).astype("float32") + tb_train = train1t.reshape(train1t.shape[0], 1).astype("float32") + ub_train = train1ub.reshape(train1ub.shape[0], 1).astype("float32") + vb_train = train1vb.reshape(train1vb.shape[0], 1).astype("float32") + wb_train = train1wb.reshape(train1wb.shape[0], 1).astype("float32") + + # generate initial data + x_0 = np.tile(x1, 31 * 31) + y_0 = np.tile(y1.repeat(31), 31) + z_0 = z1.repeat(31 * 31) + t_0 = np.array([0] * x_0.shape[0]) + u_0, v_0, w_0, p_0 = analytic_solution_generate(x_0, y_0, z_0, t_0) + u0_train = u_0.reshape(u_0.shape[0], 1).astype("float32") + v0_train = v_0.reshape(v_0.shape[0], 1).astype("float32") + w0_train = w_0.reshape(w_0.shape[0], 1).astype("float32") + x0_train = x_0.reshape(x_0.shape[0], 1).astype("float32") + y0_train = y_0.reshape(y_0.shape[0], 1).astype("float32") + z0_train = z_0.reshape(z_0.shape[0], 1).astype("float32") + t0_train = t_0.reshape(t_0.shape[0], 1).astype("float32") + + # unsupervised part + xx = np.random.randint(31, size=N_TRAIN) / 15 - 1 + yy = np.random.randint(31, size=N_TRAIN) / 15 - 1 + zz = np.random.randint(31, size=N_TRAIN) / 15 - 1 + tt = np.random.randint(11, size=N_TRAIN) / 10 + + x_train = xx.reshape(xx.shape[0], 1).astype("float32") + y_train = yy.reshape(yy.shape[0], 1).astype("float32") + z_train = zz.reshape(zz.shape[0], 1).astype("float32") + t_train = tt.reshape(tt.shape[0], 1).astype("float32") + + # test data + x_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + y_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + z_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + t_star = (np.random.randint(11, size=(1000, 1)) / 10).astype("float32") + + u_star, v_star, w_star, p_star = analytic_solution_generate( + x_star, y_star, z_star, t_star + ) + + return ( + x_train, + y_train, + z_train, + t_train, + x0_train, + y0_train, + z0_train, + t0_train, + u0_train, + v0_train, + w0_train, + xb_train, + yb_train, + zb_train, + tb_train, + ub_train, + vb_train, + wb_train, + x_star, + y_star, + z_star, + t_star, + u_star, + v_star, + w_star, + p_star, + ) + + +@hydra.main(version_base=None, config_path="./conf", config_name="VP_NSFNet3.yaml") +def main(cfg: DictConfig): + if cfg.mode == "train": + train(cfg) + elif cfg.mode == "eval": + evaluate(cfg) + else: + raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") + + +def train(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + ITERS_PER_EPOCH = cfg.iters_per_epoch + + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + # set the number of boundary samples + NB_TRAIN = cfg.nb_train + + # set the number of initial samples + N0_TRAIN = cfg.n0_train + ALPHA = cfg.alpha + BETA = cfg.beta + ( + x_train, + y_train, + z_train, + t_train, + x0_train, + y0_train, + z0_train, + t0_train, + u0_train, + v0_train, + w0_train, + xb_train, + yb_train, + zb_train, + tb_train, + ub_train, + vb_train, + wb_train, + x_star, + y_star, + z_star, + t_star, + u_star, + v_star, + w_star, + p_star, + ) = generate_data(N_TRAIN, NB_TRAIN, N0_TRAIN) + + # set dataloader config + train_dataloader_cfg_b = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": xb_train, "y": yb_train, "z": zb_train, "t": tb_train}, + "label": {"u": ub_train, "v": vb_train, "w": wb_train}, + }, + "batch_size": NB_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + train_dataloader_cfg_0 = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x0_train, "y": y0_train, "z": z0_train, "t": t0_train}, + "label": {"u": u0_train, "v": v0_train, "w": w0_train}, + }, + "batch_size": N0_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star, "z": z_star, "t": t_star}, + "label": {"u": u_star, "v": v_star, "w": w_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + geom = ppsci.geometry.PointCloud( + {"x": x_train, "y": y_train, "z": z_train, "t": t_train}, ("x", "y", "z", "t") + ) + + # supervised constraint s.t ||u-u_b|| + sup_constraint_b = ppsci.constraint.SupervisedConstraint( + train_dataloader_cfg_b, + ppsci.loss.MSELoss("mean", ALPHA), + name="Sup_b", + ) + + # supervised constraint s.t ||u-u_0|| + sup_constraint_0 = ppsci.constraint.SupervisedConstraint( + train_dataloader_cfg_0, + ppsci.loss.MSELoss("mean", BETA), + name="Sup_0", + ) + + # set equation constarint s.t. ||F(u)|| + equation = { + "NavierStokes": ppsci.equation.NavierStokes( + nu=1.0 / cfg.re, rho=1.0, dim=3, time=True + ), + } + + pde_constraint = ppsci.constraint.InteriorConstraint( + equation["NavierStokes"].equations, + {"continuity": 0, "momentum_x": 0, "momentum_y": 0, "momentum_z": 0}, + geom, + { + "dataset": {"name": "IterableNamedArrayDataset"}, + "batch_size": N_TRAIN, + "iters_per_epoch": ITERS_PER_EPOCH, + }, + ppsci.loss.MSELoss("mean"), + name="EQ", + ) + + constraint = { + pde_constraint.name: pde_constraint, + sup_constraint_b.name: sup_constraint_b, + sup_constraint_0.name: sup_constraint_0, + } + + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + # set optimizer + epoch_list = [5000, 5000, 50000, 50000] + new_epoch_list = [] + for i, _ in enumerate(epoch_list): + new_epoch_list.append(sum(epoch_list[: i + 1])) + EPOCHS = new_epoch_list[-1] + lr_list = [1e-3, 1e-4, 1e-5, 1e-6, 1e-7] + lr_scheduler = ppsci.optimizer.lr_scheduler.Piecewise( + EPOCHS, ITERS_PER_EPOCH, new_epoch_list, lr_list + )() + optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") + # initialize solver + solver = ppsci.solver.Solver( + model=model, + constraint=constraint, + optimizer=optimizer, + epochs=EPOCHS, + lr_scheduler=lr_scheduler, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=True, + log_freq=cfg.log_freq, + eval_freq=cfg.eval_freq, + seed=SEED, + equation=equation, + geom=geom, + validator=validator, + visualizer=None, + eval_with_no_grad=False, + checkpoint_path=OUTPUT_DIR + "/checkpoints/latest", + ) + # train model + solver.train() + + # evaluate after finished training + solver.eval() + solver.plot_loss_history() + + +def evaluate(cfg: DictConfig): + OUTPUT_DIR = cfg.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # set random seed for reproducibility + SEED = cfg.seed + ppsci.utils.misc.set_random_seed(SEED) + + # set model + model = ppsci.arch.MLP(**cfg.MODEL) + + # set the number of residual samples + N_TRAIN = cfg.ntrain + + # unsupervised part + xx = np.random.randint(31, size=N_TRAIN) / 15 - 1 + yy = np.random.randint(31, size=N_TRAIN) / 15 - 1 + zz = np.random.randint(31, size=N_TRAIN) / 15 - 1 + tt = np.random.randint(11, size=N_TRAIN) / 10 + + x_train = xx.reshape(xx.shape[0], 1).astype("float32") + y_train = yy.reshape(yy.shape[0], 1).astype("float32") + z_train = zz.reshape(zz.shape[0], 1).astype("float32") + t_train = tt.reshape(tt.shape[0], 1).astype("float32") + + # test data + x_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + y_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + z_star = ((np.random.rand(1000, 1) - 1 / 2) * 2).astype("float32") + t_star = (np.random.randint(11, size=(1000, 1)) / 10).astype("float32") + + u_star, v_star, w_star, p_star = analytic_solution_generate( + x_star, y_star, z_star, t_star + ) + + valida_dataloader_cfg = { + "dataset": { + "name": "NamedArrayDataset", + "input": {"x": x_star, "y": y_star, "z": z_star, "t": t_star}, + "label": {"u": u_star, "v": v_star, "w": w_star, "p": p_star}, + }, + "total_size": u_star.shape[0], + "batch_size": u_star.shape[0], + "sampler": { + "name": "BatchSampler", + "drop_last": False, + "shuffle": False, + }, + } + geom = ppsci.geometry.PointCloud( + {"x": x_train, "y": y_train, "z": z_train, "t": t_train}, ("x", "y", "z", "t") + ) + + equation = { + "NavierStokes": ppsci.equation.NavierStokes( + nu=1.0 / cfg.re, rho=1.0, dim=3, time=True + ), + } + residual_validator = ppsci.validate.SupervisedValidator( + valida_dataloader_cfg, + ppsci.loss.L2RelLoss(), + metric={"L2R": ppsci.metric.L2Rel()}, + name="Residual", + ) + + # wrap validator + validator = {residual_validator.name: residual_validator} + + # load solver + solver = ppsci.solver.Solver( + model, + equation=equation, + geom=geom, + validator=validator, + pretrained_model_path=cfg.pretrained_model_path, ### the path of the model + ) + + # print the relative error + us = [] + vs = [] + ws = [] + for i in [0, 0.25, 0.5, 0.75, 1.0]: + x_star, y_star, z_star = np.mgrid[-1.0:1.0:100j, -1.0:1.0:100j, -1.0:1.0:100j] + x_star, y_star, z_star = ( + x_star.reshape(-1, 1), + y_star.reshape(-1, 1), + z_star.reshape(-1, 1), + ) + t_star = i * np.ones(x_star.shape) + u_star, v_star, w_star, p_star = analytic_solution_generate( + x_star, y_star, z_star, t_star + ) + + solution = solver.predict({"x": x_star, "y": y_star, "z": z_star, "t": t_star}) + u_pred = solution["u"] + v_pred = solution["v"] + w_pred = solution["w"] + p_pred = solution["p"] + p_pred = p_pred - p_pred.mean() + p_star.mean() + error_u = np.linalg.norm(u_star - u_pred, 2) / np.linalg.norm(u_star, 2) + error_v = np.linalg.norm(v_star - v_pred, 2) / np.linalg.norm(v_star, 2) + error_w = np.linalg.norm(w_star - w_pred, 2) / np.linalg.norm(w_star, 2) + error_p = np.linalg.norm(p_star - p_pred, 2) / np.linalg.norm(p_star, 2) + us.append(error_u) + vs.append(error_v) + ws.append(error_w) + print("t={:.2f},relative error of u: {:.3e}".format(t_star[0].item(), error_u)) + print("t={:.2f},relative error of v: {:.3e}".format(t_star[0].item(), error_v)) + print("t={:.2f},relative error of w: {:.3e}".format(t_star[0].item(), error_w)) + print("t={:.2f},relative error of p: {:.3e}".format(t_star[0].item(), error_p)) + + ## plot vorticity + grid_x, grid_y = np.mgrid[-1.0:1.0:1000j, -1.0:1.0:1000j] + grid_x = grid_x.reshape(-1, 1) + grid_y = grid_y.reshape(-1, 1) + grid_z = np.zeros(grid_x.shape) + T = np.linspace(0, 1, 20) + for i in T: + t_star = i * np.ones(x_star.shape) + u_star, v_star, w_star, p_star = analytic_solution_generate( + grid_x, grid_y, grid_z, t_star + ) + + solution = solver.predict({"x": grid_x, "y": grid_y, "z": grid_z, "t": t_star}) + u_pred = np.array(solution["u"]) + v_pred = np.array(solution["v"]) + w_pred = np.array(solution["w"]) + p_pred = p_pred - p_pred.mean() + p_star.mean() + fig, ax = plt.subplots(3, 2, figsize=(12, 12)) + ax[0, 0].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + u_star.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[0, 1].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + u_pred.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[1, 0].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + v_star.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[1, 1].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + v_pred.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[2, 0].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + w_star.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[2, 1].contourf( + grid_x.reshape(1000, 1000), + grid_y.reshape(1000, 1000), + w_pred.reshape(1000, 1000), + cmap=plt.get_cmap("RdYlBu"), + ) + ax[0, 0].set_title("u_exact") + ax[0, 1].set_title("u_pred") + ax[1, 0].set_title("v_exact") + ax[1, 1].set_title("v_pred") + ax[2, 0].set_title("w_exact") + ax[2, 1].set_title("w_pred") + fig.savefig(OUTPUT_DIR + f"/velocity_t={i}.png") + + +if __name__ == "__main__": + main() diff --git a/examples/NSFNet/conf/VP_NSFNet1.yaml b/examples/NSFNet/conf/VP_NSFNet1.yaml new file mode 100644 index 000000000..af50c31b9 --- /dev/null +++ b/examples/NSFNet/conf/VP_NSFNet1.yaml @@ -0,0 +1,31 @@ +seed: 1234 + +output_dir: ./output + +iters_per_epoch: 1 + +MODEL: + input_keys: ["x", "y"] + output_keys: ["u", "v", "p"] + num_layers: 4 + hidden_size: 50 + activation: "tanh" + +mode: train + +ntrain: 2601 + +nb_train: 400 + +re: 40 + +log_freq: 5000 + +eval_freq: 5000 + +epoch_list: [5000, 5000, 50000, 50000] + +lr_list: [1e-3, 1e-4, 1e-5, 1e-6, 1e-7] + + + diff --git a/examples/NSFNet/conf/VP_NSFNet2.yaml b/examples/NSFNet/conf/VP_NSFNet2.yaml new file mode 100644 index 000000000..593c10439 --- /dev/null +++ b/examples/NSFNet/conf/VP_NSFNet2.yaml @@ -0,0 +1,34 @@ +seed: 1234 + +output_dir: ./output_NSFNet2 + +data_dir: ./npy_data/cylinder_nektar_wake.mat + +iters_per_epoch: 1 + +MODEL: + input_keys: ["x", "y","t"] + output_keys: ["u", "v", "p"] + num_layers: 10 + hidden_size: 100 + activation: "tanh" + +mode: eval + +ntrain: 140000 + +nb_train: 21300 + +n0_train: 5000 + +re: 100 + +log_freq: 5000 + +eval_freq: 100 + +epoch_list: [5000, 5000, 50000, 50000] + +lr_list: [1e-3, 1e-4, 1e-5, 1e-6, 1e-7] + +pretrained_model_path: ./output_NSFNet2/checkpoints/latest \ No newline at end of file diff --git a/examples/NSFNet/conf/VP_NSFNet3.yaml b/examples/NSFNet/conf/VP_NSFNet3.yaml new file mode 100644 index 000000000..1ba36b32c --- /dev/null +++ b/examples/NSFNet/conf/VP_NSFNet3.yaml @@ -0,0 +1,37 @@ +seed: 1234 + +output_dir: ./output_NSFNet3 + +iters_per_epoch: 1 + +MODEL: + input_keys: ["x", "y","z","t"] + output_keys: ["u", "v", "w","p"] + num_layers: 10 + hidden_size: 100 + activation: "tanh" + +mode: eval + +ntrain: 70000 + +nb_train: 59400 + +n0_train: 29791 + +alpha: 100 + +beta: 100 + +re: 1 + +log_freq: 5000 + +eval_freq: 5000 + +epoch_list: [5000, 5000, 50000, 50000] + +lr_list: [1e-3, 1e-4, 1e-5, 1e-6, 1e-7] + +pretrained_model_path: ./output_NSFNet3/checkpoints/latest + diff --git a/examples/aneurysm/aneurysm.py b/examples/aneurysm/aneurysm.py index b8a9022ea..2d34ae0dc 100644 --- a/examples/aneurysm/aneurysm.py +++ b/examples/aneurysm/aneurysm.py @@ -235,7 +235,7 @@ def inlet_w_ref_func(_in): # set visualizer(optional) visualizer = { - "visualize_u_v_w_p": ppsci.visualize.VisualizerVtu( + "visulzie_u_v_w_p": ppsci.visualize.VisualizerVtu( input_dict, { "p": lambda out: out["p"], diff --git a/examples/aneurysm/aneurysm_flow.py b/examples/aneurysm/aneurysm_flow.py index 1d327a023..0a2661d58 100644 --- a/examples/aneurysm/aneurysm_flow.py +++ b/examples/aneurysm/aneurysm_flow.py @@ -56,10 +56,10 @@ mu = 0.5 * (X_OUT - X_IN) N_Y = 20 - x_initial = np.linspace(X_IN, X_OUT, 100, dtype=paddle.get_default_dtype()).reshape( + x_inital = np.linspace(X_IN, X_OUT, 100, dtype=paddle.get_default_dtype()).reshape( 100, 1 ) - x_20_copy = np.tile(x_initial, (20, 1)) # duplicate 20 times of x for dataloader + x_20_copy = np.tile(x_inital, (20, 1)) # duplicate 20 times of x for dataloader SIGMA = 0.1 SCALE_START = -0.02 @@ -73,7 +73,7 @@ len(scale), 1 ) - # Axisymmetric boundary + # Axisymetric boundary r_func = ( scale / math.sqrt(2 * np.pi * SIGMA**2) @@ -85,18 +85,18 @@ os.makedirs(PLOT_DIR, exist_ok=True) y_up = (R_INLET - r_func) * np.ones_like(x) y_down = (-R_INLET + r_func) * np.ones_like(x) - idx = np.where(scale == 0) # plot vessel which scale is 0.2 by finding its indices + idx = np.where(scale == 0) # plot vessel which scale is 0.2 by finding its indexs plt.figure() plt.scatter(x[idx], y_up[idx]) plt.scatter(x[idx], y_down[idx]) plt.axis("equal") - plt.savefig(osp.join(PLOT_DIR, "idealized_stenotic_vessel"), bbox_inches="tight") + plt.savefig(osp.join(PLOT_DIR, "idealized_stenotid_vessel"), bbox_inches="tight") # Points and shuffle(for alignment) y = np.zeros([len(x), 1], dtype=paddle.get_default_dtype()) - for x0 in x_initial: + for x0 in x_inital: index = np.where(x[:, 0] == x0)[0] - # y is linear to scale, so we place linspace to get 1000 x, it corresponds to vessels + # y is linear to scale, so we place linespace to get 1000 x, it coressponds to vessels y[index] = np.linspace( -max(y_up[index]), max(y_up[index]), @@ -104,7 +104,7 @@ dtype=paddle.get_default_dtype(), ).reshape(len(index), -1) - idx = np.where(scale == 0) # plot vessel which scale is 0.2 by finding its indices + idx = np.where(scale == 0) # plot vessel which scale is 0.2 by finding its indexs plt.figure() plt.scatter(x[idx], y[idx]) plt.axis("equal") @@ -274,7 +274,7 @@ def model_predict( ) # error_p = np.linalg.norm(p - p_cfd) / (D_P * D_P) - # Stream-wise velocity component u + # Streamwise velocity component u plt.figure() plt.subplot(212) plt.scatter(x, y, c=u_vec[:, 0], vmin=min(u_cfd[:, 0]), vmax=max(u_cfd[:, 0])) @@ -291,7 +291,7 @@ def model_predict( bbox_inches="tight", ) - # Span-wise velocity component v + # Spanwise velocity component v plt.figure() plt.subplot(212) plt.scatter(x, y, c=u_vec[:, 1], vmin=min(u_cfd[:, 1]), vmax=max(u_cfd[:, 1])) @@ -311,10 +311,10 @@ def model_predict( # Centerline wall shear profile tau_c (downside) data_CFD_wss = np.load(osp.join(path, f"{case_id}CFD_wss.npz")) - x_initial = data_CFD_wss["x"] + x_inital = data_CFD_wss["x"] wall_shear_mag_up = data_CFD_wss["wss"] - D_H = 0.001 # The span-wise distance is approximately the height of the wall + D_H = 0.001 # The spanwise distance is approximately the height of the wall r_cl = ( scale / np.sqrt(2 * np.pi * SIGMA**2) @@ -337,7 +337,7 @@ def model_predict( plt.figure() plt.plot( - x_initial, + x_inital, wall_shear_mag_up, label="CFD", color="darkblue", @@ -346,7 +346,7 @@ def model_predict( alpha=1.0, ) plt.plot( - x_initial, + x_inital, tau_c, label="DNN", color="red", diff --git a/examples/bracket/bracket.py b/examples/bracket/bracket.py index b9141beba..f2dfcc9c0 100644 --- a/examples/bracket/bracket.py +++ b/examples/bracket/bracket.py @@ -4,64 +4,77 @@ pretrained model download link: https://paddle-org.bj.bcebos.com/paddlescience/models/bracket/bracket_pretrained.pdparams """ -from os import path as osp - -import hydra import numpy as np -from omegaconf import DictConfig import ppsci +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + SEED = 2023 + ppsci.utils.misc.set_random_seed(SEED) + # set output directory + OUTPUT_DIR = "./output_bracket" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - disp_net = ppsci.arch.MLP(**cfg.MODEL.disp_net) - stress_net = ppsci.arch.MLP(**cfg.MODEL.stress_net) + disp_net = ppsci.arch.MLP( + ("x", "y", "z"), ("u", "v", "w"), 6, 512, "silu", weight_norm=True + ) + stress_net = ppsci.arch.MLP( + ("x", "y", "z"), + ("sigma_xx", "sigma_yy", "sigma_zz", "sigma_xy", "sigma_xz", "sigma_yz"), + 6, + 512, + "silu", + weight_norm=True, + ) # wrap to a model_list model = ppsci.arch.ModelList((disp_net, stress_net)) - # specify parameters - LAMBDA_ = cfg.NU * cfg.E / ((1 + cfg.NU) * (1 - 2 * cfg.NU)) - MU = cfg.E / (2 * (1 + cfg.NU)) + # Specify parameters + NU = 0.3 + E = 100.0e9 + LAMBDA_ = NU * E / ((1 + NU) * (1 - 2 * NU)) + MU = E / (2 * (1 + NU)) MU_C = 0.01 * MU LAMBDA_ = LAMBDA_ / MU_C MU = MU / MU_C - SIGMA_NORMALIZATION = cfg.CHARACTERISTIC_LENGTH / ( - cfg.CHARACTERISTIC_DISPLACEMENT * MU_C - ) + CHARACTERISTIC_LENGTH = 1.0 + CHARACTERISTIC_DISPLACEMENT = 1.0e-4 + SIGMA_NORMALIZATION = CHARACTERISTIC_LENGTH / (CHARACTERISTIC_DISPLACEMENT * MU_C) T = -4.0e4 * SIGMA_NORMALIZATION # set equation equation = { "LinearElasticity": ppsci.equation.LinearElasticity( - lambda_=LAMBDA_, mu=MU, dim=3 + E=None, nu=None, lambda_=LAMBDA_, mu=MU, dim=3 ) } # set geometry - support = ppsci.geometry.Mesh(cfg.SUPPORT_PATH) - bracket = ppsci.geometry.Mesh(cfg.BRACKET_PATH) - aux_lower = ppsci.geometry.Mesh(cfg.AUX_LOWER_PATH) - aux_upper = ppsci.geometry.Mesh(cfg.AUX_UPPER_PATH) - cylinder_hole = ppsci.geometry.Mesh(cfg.CYLINDER_HOLE_PATH) - cylinder_lower = ppsci.geometry.Mesh(cfg.CYLINDER_LOWER_PATH) - cylinder_upper = ppsci.geometry.Mesh(cfg.CYLINDER_UPPER_PATH) + support = ppsci.geometry.Mesh("./stl/support.stl") + bracket = ppsci.geometry.Mesh("./stl/bracket.stl") + aux_lower = ppsci.geometry.Mesh("./stl/aux_lower.stl") + aux_upper = ppsci.geometry.Mesh("./stl/aux_upper.stl") + cylinder_hole = ppsci.geometry.Mesh("./stl/cylinder_hole.stl") + cylinder_lower = ppsci.geometry.Mesh("./stl/cylinder_lower.stl") + cylinder_upper = ppsci.geometry.Mesh("./stl/cylinder_upper.stl") # geometry bool operation curve_lower = aux_lower - cylinder_lower curve_upper = aux_upper - cylinder_upper geo = support + bracket + curve_lower + curve_upper - cylinder_hole + geom = {"geo": geo} # set dataloader config + ITERS_PER_EPOCH = 1000 train_dataloader_cfg = { "dataset": "NamedArrayDataset", - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "iters_per_epoch": ITERS_PER_EPOCH, "sampler": { "name": "BatchSampler", "drop_last": True, @@ -85,17 +98,17 @@ def train(cfg: DictConfig): {"u": lambda d: d["u"], "v": lambda d: d["v"], "w": lambda d: d["w"]}, {"u": 0, "v": 0, "w": 0}, geom["geo"], - {**train_dataloader_cfg, "batch_size": cfg.TRAIN.batch_size.bc_back}, + {**train_dataloader_cfg, "batch_size": 1024}, ppsci.loss.MSELoss("sum"), criteria=lambda x, y, z: x == SUPPORT_ORIGIN[0], - weight_dict=cfg.TRAIN.weight.bc_back, + weight_dict={"u": 10, "v": 10, "w": 10}, name="BC_BACK", ) bc_front = ppsci.constraint.BoundaryConstraint( equation["LinearElasticity"].equations, {"traction_x": 0, "traction_y": 0, "traction_z": T}, geom["geo"], - {**train_dataloader_cfg, "batch_size": cfg.TRAIN.batch_size.bc_front}, + {**train_dataloader_cfg, "batch_size": 128}, ppsci.loss.MSELoss("sum"), criteria=lambda x, y, z: x == BRACKET_ORIGIN[0] + BRACKET_DIM[0], name="BC_FRONT", @@ -104,14 +117,14 @@ def train(cfg: DictConfig): equation["LinearElasticity"].equations, {"traction_x": 0, "traction_y": 0, "traction_z": 0}, geom["geo"], - {**train_dataloader_cfg, "batch_size": cfg.TRAIN.batch_size.bc_surface}, + {**train_dataloader_cfg, "batch_size": 4096}, ppsci.loss.MSELoss("sum"), criteria=lambda x, y, z: np.logical_and( x > SUPPORT_ORIGIN[0] + 1e-7, x < BRACKET_ORIGIN[0] + BRACKET_DIM[0] - 1e-7 ), name="BC_SURFACE", ) - support_interior = ppsci.constraint.InteriorConstraint( + support_interior_constraint = ppsci.constraint.InteriorConstraint( equation["LinearElasticity"].equations, { "stress_disp_xx": 0, @@ -125,7 +138,7 @@ def train(cfg: DictConfig): "equilibrium_z": 0, }, geom["geo"], - {**train_dataloader_cfg, "batch_size": cfg.TRAIN.batch_size.support_interior}, + {**train_dataloader_cfg, "batch_size": 2048}, ppsci.loss.MSELoss("sum"), criteria=lambda x, y, z: ( (BOUNDS_SUPPORT_X[0] < x) @@ -146,9 +159,9 @@ def train(cfg: DictConfig): "equilibrium_y": "sdf", "equilibrium_z": "sdf", }, - name="SUPPORT_INTERIOR", + name="support_interior", ) - bracket_interior = ppsci.constraint.InteriorConstraint( + bracket_interior_constraint = ppsci.constraint.InteriorConstraint( equation["LinearElasticity"].equations, { "stress_disp_xx": 0, @@ -162,7 +175,7 @@ def train(cfg: DictConfig): "equilibrium_z": 0, }, geom["geo"], - {**train_dataloader_cfg, "batch_size": cfg.TRAIN.batch_size.bracket_interior}, + {**train_dataloader_cfg, "batch_size": 1024}, ppsci.loss.MSELoss("sum"), criteria=lambda x, y, z: ( (BOUNDS_BRACKET_X[0] < x) @@ -183,26 +196,34 @@ def train(cfg: DictConfig): "equilibrium_y": "sdf", "equilibrium_z": "sdf", }, - name="BRACKET_INTERIOR", + name="bracket_interior", ) # wrap constraints together constraint = { bc_back.name: bc_back, bc_front.name: bc_front, bc_surface.name: bc_surface, - support_interior.name: support_interior, - bracket_interior.name: bracket_interior, + support_interior_constraint.name: support_interior_constraint, + bracket_interior_constraint.name: bracket_interior_constraint, } + # set training hyper-parameters + EPOCHS = 2000 if not args.epochs else args.epochs + # set optimizer lr_scheduler = ppsci.optimizer.lr_scheduler.ExponentialDecay( - **cfg.TRAIN.lr_scheduler + EPOCHS, + ITERS_PER_EPOCH, + 0.001, + 0.95, + 15000, + by_epoch=False, )() optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) # set validator ref_xyzu = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_X_PATH, + "./data/deformation_x.txt", ("x", "y", "z", "u"), { "x": "X Location (m)", @@ -213,51 +234,51 @@ def train(cfg: DictConfig): "\t", ) ref_v = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_Y_PATH, + "./data/deformation_y.txt", ("v",), {"v": "Directional Deformation (m)"}, "\t", ) ref_w = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_Z_PATH, + "./data/deformation_z.txt", ("w",), {"w": "Directional Deformation (m)"}, "\t", ) ref_sxx = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_X_PATH, + "./data/normal_x.txt", ("sigma_xx",), {"sigma_xx": "Normal Stress (Pa)"}, "\t", ) ref_syy = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_Y_PATH, + "./data/normal_y.txt", ("sigma_yy",), {"sigma_yy": "Normal Stress (Pa)"}, "\t", ) ref_szz = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_Z_PATH, + "./data/normal_z.txt", ("sigma_zz",), {"sigma_zz": "Normal Stress (Pa)"}, "\t", ) ref_sxy = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_XY_PATH, + "./data/shear_xy.txt", ("sigma_xy",), {"sigma_xy": "Shear Stress (Pa)"}, "\t", ) ref_sxz = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_XZ_PATH, + "./data/shear_xz.txt", ("sigma_xz",), {"sigma_xz": "Shear Stress (Pa)"}, "\t", ) ref_syz = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_YZ_PATH, + "./data/shear_yz.txt", ("sigma_yz",), {"sigma_yz": "Shear Stress (Pa)"}, "\t", @@ -269,9 +290,9 @@ def train(cfg: DictConfig): "z": ref_xyzu["z"], } label_dict = { - "u": ref_xyzu["u"] / cfg.CHARACTERISTIC_DISPLACEMENT, - "v": ref_v["v"] / cfg.CHARACTERISTIC_DISPLACEMENT, - "w": ref_w["w"] / cfg.CHARACTERISTIC_DISPLACEMENT, + "u": ref_xyzu["u"] / CHARACTERISTIC_DISPLACEMENT, + "v": ref_v["v"] / CHARACTERISTIC_DISPLACEMENT, + "w": ref_w["w"] / CHARACTERISTIC_DISPLACEMENT, "sigma_xx": ref_sxx["sigma_xx"] * SIGMA_NORMALIZATION, "sigma_yy": ref_syy["sigma_yy"] * SIGMA_NORMALIZATION, "sigma_zz": ref_szz["sigma_zz"] * SIGMA_NORMALIZATION, @@ -292,7 +313,7 @@ def train(cfg: DictConfig): }, } sup_validator = ppsci.validate.SupervisedValidator( - {**eval_dataloader_cfg, "batch_size": cfg.EVAL.batch_size.sup_validator}, + {**eval_dataloader_cfg, "batch_size": 128}, ppsci.loss.MSELoss("mean"), { "u": lambda out: out["u"], @@ -312,7 +333,7 @@ def train(cfg: DictConfig): # set visualizer(optional) visualizer = { - "visualize_u_v_w_sigmas": ppsci.visualize.VisualizerVtu( + "visulzie_u_v_w_sigmas": ppsci.visualize.VisualizerVtu( input_dict, { "u": lambda out: out["u"], @@ -333,22 +354,21 @@ def train(cfg: DictConfig): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, lr_scheduler, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - save_freq=cfg.TRAIN.save_freq, - log_freq=cfg.log_freq, - eval_during_train=cfg.TRAIN.eval_during_train, - eval_freq=cfg.TRAIN.eval_freq, - seed=cfg.seed, + EPOCHS, + ITERS_PER_EPOCH, + save_freq=20, + log_freq=20, + eval_during_train=True, + eval_freq=20, + seed=SEED, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - checkpoint_path=cfg.TRAIN.checkpoint_path, - eval_with_no_grad=cfg.EVAL.eval_with_no_grad, + eval_with_no_grad=True, ) # train model solver.train() @@ -358,184 +378,19 @@ def train(cfg: DictConfig): # visualize prediction after finished training solver.visualize() - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "eval.log"), "info") - - # set model - disp_net = ppsci.arch.MLP(**cfg.MODEL.disp_net) - stress_net = ppsci.arch.MLP(**cfg.MODEL.stress_net) - # wrap to a model_list - model = ppsci.arch.ModelList((disp_net, stress_net)) - - # Specify parameters - LAMBDA_ = cfg.NU * cfg.E / ((1 + cfg.NU) * (1 - 2 * cfg.NU)) - MU = cfg.E / (2 * (1 + cfg.NU)) - MU_C = 0.01 * MU - LAMBDA_ = LAMBDA_ / MU_C - MU = MU / MU_C - SIGMA_NORMALIZATION = cfg.CHARACTERISTIC_LENGTH / ( - cfg.CHARACTERISTIC_DISPLACEMENT * MU_C - ) - - # set validator - ref_xyzu = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_X_PATH, - ("x", "y", "z", "u"), - { - "x": "X Location (m)", - "y": "Y Location (m)", - "z": "Z Location (m)", - "u": "Directional Deformation (m)", - }, - "\t", - ) - ref_v = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_Y_PATH, - ("v",), - {"v": "Directional Deformation (m)"}, - "\t", - ) - ref_w = ppsci.utils.reader.load_csv_file( - cfg.DEFORMATION_Z_PATH, - ("w",), - {"w": "Directional Deformation (m)"}, - "\t", - ) - - ref_sxx = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_X_PATH, - ("sigma_xx",), - {"sigma_xx": "Normal Stress (Pa)"}, - "\t", - ) - ref_syy = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_Y_PATH, - ("sigma_yy",), - {"sigma_yy": "Normal Stress (Pa)"}, - "\t", - ) - ref_szz = ppsci.utils.reader.load_csv_file( - cfg.NORMAL_Z_PATH, - ("sigma_zz",), - {"sigma_zz": "Normal Stress (Pa)"}, - "\t", - ) - - ref_sxy = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_XY_PATH, - ("sigma_xy",), - {"sigma_xy": "Shear Stress (Pa)"}, - "\t", - ) - ref_sxz = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_XZ_PATH, - ("sigma_xz",), - {"sigma_xz": "Shear Stress (Pa)"}, - "\t", - ) - ref_syz = ppsci.utils.reader.load_csv_file( - cfg.SHEAR_YZ_PATH, - ("sigma_yz",), - {"sigma_yz": "Shear Stress (Pa)"}, - "\t", - ) - - input_dict = { - "x": ref_xyzu["x"], - "y": ref_xyzu["y"], - "z": ref_xyzu["z"], - } - label_dict = { - "u": ref_xyzu["u"] / cfg.CHARACTERISTIC_DISPLACEMENT, - "v": ref_v["v"] / cfg.CHARACTERISTIC_DISPLACEMENT, - "w": ref_w["w"] / cfg.CHARACTERISTIC_DISPLACEMENT, - "sigma_xx": ref_sxx["sigma_xx"] * SIGMA_NORMALIZATION, - "sigma_yy": ref_syy["sigma_yy"] * SIGMA_NORMALIZATION, - "sigma_zz": ref_szz["sigma_zz"] * SIGMA_NORMALIZATION, - "sigma_xy": ref_sxy["sigma_xy"] * SIGMA_NORMALIZATION, - "sigma_xz": ref_sxz["sigma_xz"] * SIGMA_NORMALIZATION, - "sigma_yz": ref_syz["sigma_yz"] * SIGMA_NORMALIZATION, - } - eval_dataloader_cfg = { - "dataset": { - "name": "NamedArrayDataset", - "input": input_dict, - "label": label_dict, - }, - "sampler": { - "name": "BatchSampler", - "drop_last": False, - "shuffle": False, - }, - } - sup_validator = ppsci.validate.SupervisedValidator( - {**eval_dataloader_cfg, "batch_size": cfg.EVAL.batch_size.sup_validator}, - ppsci.loss.MSELoss("mean"), - { - "u": lambda out: out["u"], - "v": lambda out: out["v"], - "w": lambda out: out["w"], - "sigma_xx": lambda out: out["sigma_xx"], - "sigma_yy": lambda out: out["sigma_yy"], - "sigma_zz": lambda out: out["sigma_zz"], - "sigma_xy": lambda out: out["sigma_xy"], - "sigma_xz": lambda out: out["sigma_xz"], - "sigma_yz": lambda out: out["sigma_yz"], - }, - metric={"MSE": ppsci.metric.MSE()}, - name="commercial_ref_u_v_w_sigmas", - ) - validator = {sup_validator.name: sup_validator} - - # set visualizer(optional) - visualizer = { - "visualize_u_v_w_sigmas": ppsci.visualize.VisualizerVtu( - input_dict, - { - "u": lambda out: out["u"], - "v": lambda out: out["v"], - "w": lambda out: out["w"], - "sigma_xx": lambda out: out["sigma_xx"], - "sigma_yy": lambda out: out["sigma_yy"], - "sigma_zz": lambda out: out["sigma_zz"], - "sigma_xy": lambda out: out["sigma_xy"], - "sigma_xz": lambda out: out["sigma_xz"], - "sigma_yz": lambda out: out["sigma_yz"], - }, - prefix="result_u_v_w_sigmas", - ) - } - - # initialize solver + # directly evaluate pretrained model(optional) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") solver = ppsci.solver.Solver( model, - output_dir=cfg.output_dir, - log_freq=cfg.log_freq, - seed=cfg.seed, + constraint, + OUTPUT_DIR, + equation=equation, + geom=geom, validator=validator, visualizer=visualizer, - pretrained_model_path=cfg.EVAL.pretrained_model_path, - eval_with_no_grad=cfg.EVAL.eval_with_no_grad, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", + eval_with_no_grad=True, ) - # evaluate after finished training solver.eval() - # visualize prediction after finished training + # visualize prediction for pretrained model(optional) solver.visualize() - - -@hydra.main(version_base=None, config_path="./conf", config_name="bracket.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/bubble/bubble.py b/examples/bubble/bubble.py index 10f2cb475..a74b690c1 100644 --- a/examples/bubble/bubble.py +++ b/examples/bubble/bubble.py @@ -17,28 +17,27 @@ Bubble data files download link: https://paddle-org.bj.bcebos.com/paddlescience/datasets/BubbleNet/bubble.mat """ -from os import path as osp - -import hydra import numpy as np import paddle -import scipy -from omegaconf import DictConfig +import scipy.io import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) + # set output directory + OUTPUT_DIR = "./output_bubble" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # load Data - data = scipy.io.loadmat(cfg.DATA_PATH) + data = scipy.io.loadmat("bubble.mat") # normalize data p_max = data["p"].max(axis=0) p_min = data["p"].min(axis=0) @@ -84,9 +83,9 @@ def train(cfg: DictConfig): test_label = {"u": u, "v": v, "p": p, "phil": phil} # set model - model_psi = ppsci.arch.MLP(**cfg.MODEL.psi_net) - model_p = ppsci.arch.MLP(**cfg.MODEL.p_net) - model_phil = ppsci.arch.MLP(**cfg.MODEL.phil_net) + model_psi = ppsci.arch.MLP(("t", "x", "y"), ("psi",), 9, 30, "tanh") + model_p = ppsci.arch.MLP(("t", "x", "y"), ("p",), 9, 30, "tanh") + model_phil = ppsci.arch.MLP(("t", "x", "y"), ("phil",), 9, 30, "tanh") # transform def transform_out(in_, out): @@ -119,6 +118,7 @@ def transform_out(in_, out): NPOINT_PDE, NTIME_PDE = 300 * 100, NTIME_ALL - 1 # set constraint + ITERS_PER_EPOCH = 1 pde_constraint = ppsci.constraint.InteriorConstraint( { "pressure_Poisson": lambda out: hessian(out["p"], out["x"]) @@ -128,8 +128,8 @@ def transform_out(in_, out): geom["time_rect"], { "dataset": "IterableNamedArrayDataset", - "batch_size": cfg.TRAIN.batch_size.pde_constraint, - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "batch_size": 228595, + "iters_per_epoch": ITERS_PER_EPOCH, }, ppsci.loss.MSELoss("mean"), name="EQ", @@ -142,7 +142,7 @@ def transform_out(in_, out): "input": train_input, "label": train_label, }, - "batch_size": cfg.TRAIN.batch_size.sup_constraint, + "batch_size": 2419, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -159,8 +159,11 @@ def transform_out(in_, out): pde_constraint.name: pde_constraint, } + # set training hyper-parameters + EPOCHS = 10000 if not args.epochs else args.epochs + EVAL_FREQ = 1000 # set optimizer - optimizer = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_list) + optimizer = ppsci.optimizer.Adam(0.001)(model_list) # set validator mse_validator = ppsci.validate.SupervisedValidator( @@ -170,7 +173,7 @@ def transform_out(in_, out): "input": test_input, "label": test_label, }, - "batch_size": cfg.TRAIN.batch_size.mse_validator, + "batch_size": 2419, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -189,13 +192,13 @@ def transform_out(in_, out): solver = ppsci.solver.Solver( model_list, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - eval_freq=cfg.TRAIN.eval_freq, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=EVAL_FREQ, geom=geom, validator=validator, ) @@ -204,155 +207,14 @@ def transform_out(in_, out): # evaluate after finished training solver.eval() - # visualize prediction after finished training - visu_mat = geom["time_rect_visu"].sample_interior( - NPOINT_PDE * NTIME_PDE, evenly=True - ) - - pred_norm = solver.predict(visu_mat, no_grad=False, return_numpy=True) - # inverse normalization - p_pred = pred_norm["p"].reshape([NTIME_PDE, NPOINT_PDE]).T - u_pred = pred_norm["u"].reshape([NTIME_PDE, NPOINT_PDE]).T - v_pred = pred_norm["v"].reshape([NTIME_PDE, NPOINT_PDE]).T - pred = { - "p": (p_pred * (p_max - p_min) + p_min).T.reshape([-1, 1]), - "u": (u_pred * (u_max - u_min) + u_min).T.reshape([-1, 1]), - "v": (v_pred * (v_max - v_min) + v_min).T.reshape([-1, 1]), - "phil": pred_norm["phil"], - } - ppsci.visualize.save_vtu_from_dict( - osp.join(cfg.output_dir, "visual/result.vtu"), - { - "t": visu_mat["t"], - "x": visu_mat["x"], - "y": visu_mat["y"], - "u": pred["u"], - "v": pred["v"], - "p": pred["p"], - "phil": pred["phil"], - }, - ("t", "x", "y"), - ("u", "v", "p", "phil"), - NTIME_PDE, - ) - - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") - - # load Data - data = scipy.io.loadmat(cfg.DATA_PATH) - # normalize data - p_max = data["p"].max(axis=0) - p_min = data["p"].min(axis=0) - p_norm = (data["p"] - p_min) / (p_max - p_min) - u_max = data["u"].max(axis=0) - u_min = data["u"].min(axis=0) - u_norm = (data["u"] - u_min) / (u_max - u_min) - v_max = data["v"].max(axis=0) - v_min = data["v"].min(axis=0) - v_norm = (data["v"] - v_min) / (v_max - v_min) - - u_star = u_norm # N x T - v_star = v_norm # N x T - p_star = p_norm # N x T - phil_star = data["phil"] # N x T - t_star = data["t"] # T x 1 - x_star = data["X"] # N x 2 - - N = x_star.shape[0] - T = t_star.shape[0] - - # rearrange data - xx = np.tile(x_star[:, 0:1], (1, T)) # N x T - yy = np.tile(x_star[:, 1:2], (1, T)) # N x T - tt = np.tile(t_star, (1, N)).T # N x T - - x = xx.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - y = yy.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - t = tt.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - - u = u_star.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - v = v_star.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - p = p_star.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - phil = phil_star.flatten()[:, None].astype(paddle.get_default_dtype()) # NT x 1 - - idx = np.random.choice(N * T, int(N * T * 0.75), replace=False) - # train data - train_input = {"x": x[idx, :], "y": y[idx, :], "t": t[idx, :]} - - # eval data - test_input = {"x": x, "y": y, "t": t} - test_label = {"u": u, "v": v, "p": p, "phil": phil} - - # set model - model_psi = ppsci.arch.MLP(**cfg.MODEL.psi_net) - model_p = ppsci.arch.MLP(**cfg.MODEL.p_net) - model_phil = ppsci.arch.MLP(**cfg.MODEL.phil_net) - - # transform - def transform_out(in_, out): - psi_y = out["psi"] - y = in_["y"] - x = in_["x"] - u = jacobian(psi_y, y, create_graph=False) - v = -jacobian(psi_y, x, create_graph=False) - return {"u": u, "v": v} - - # register transform - model_psi.register_output_transform(transform_out) - model_list = ppsci.arch.ModelList((model_psi, model_p, model_phil)) - - # set time-geometry - # set timestamps(including initial t0) - timestamps = np.linspace(0, 126, 127, endpoint=True) - geom = { - "time_rect": ppsci.geometry.PointCloud( - train_input, - ("t", "x", "y"), - ), - "time_rect_visu": ppsci.geometry.TimeXGeometry( - ppsci.geometry.TimeDomain(1, 126, timestamps=timestamps), - ppsci.geometry.Rectangle((0, 0), (15, 5)), - ), - } - - NTIME_ALL = len(timestamps) - NPOINT_PDE, NTIME_PDE = 300 * 100, NTIME_ALL - 1 - - # set validator - mse_validator = ppsci.validate.SupervisedValidator( - { - "dataset": { - "name": "NamedArrayDataset", - "input": test_input, - "label": test_label, - }, - "batch_size": cfg.TRAIN.batch_size.mse_validator, - "sampler": { - "name": "BatchSampler", - "drop_last": False, - "shuffle": False, - }, - }, - ppsci.loss.MSELoss("mean"), - metric={"MSE": ppsci.metric.MSE()}, - name="bubble_mse", - ) - validator = { - mse_validator.name: mse_validator, - } - # directly evaluate pretrained model(optional) solver = ppsci.solver.Solver( model_list, - output_dir=cfg.output_dir, + constraint, + OUTPUT_DIR, geom=geom, validator=validator, - pretrained_model_path=cfg.EVAL.pretrained_model_path, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", ) solver.eval() @@ -373,7 +235,7 @@ def transform_out(in_, out): "phil": pred_norm["phil"], } ppsci.visualize.save_vtu_from_dict( - osp.join(cfg.output_dir, "visual/result.vtu"), + "f{OUTPUT_DIR}/visual/result.vtu", { "t": visu_mat["t"], "x": visu_mat["x"], @@ -387,17 +249,3 @@ def transform_out(in_, out): ("u", "v", "p", "phil"), NTIME_PDE, ) - - -@hydra.main(version_base=None, config_path="./conf", config_name="bubble.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/cylinder/2d_unsteady/cylinder2d_unsteady_Re100.py b/examples/cylinder/2d_unsteady/cylinder2d_unsteady_Re100.py index f13e0431a..8039ecc86 100644 --- a/examples/cylinder/2d_unsteady/cylinder2d_unsteady_Re100.py +++ b/examples/cylinder/2d_unsteady/cylinder2d_unsteady_Re100.py @@ -202,7 +202,7 @@ evenly=True, ) visualizer = { - "visualize_u_v_p": ppsci.visualize.VisualizerVtu( + "visulzie_u_v_p": ppsci.visualize.VisualizerVtu( vis_points, {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, num_timestamps=NUM_TIMESTAMPS, diff --git a/examples/cylinder/2d_unsteady/transformer_physx/train_transformer.py b/examples/cylinder/2d_unsteady/transformer_physx/train_transformer.py index 149c02214..636751eb8 100644 --- a/examples/cylinder/2d_unsteady/transformer_physx/train_transformer.py +++ b/examples/cylinder/2d_unsteady/transformer_physx/train_transformer.py @@ -177,7 +177,7 @@ def __call__(self, x: Dict[str, paddle.Tensor]) -> Dict[str, paddle.Tensor]: } visualizer = { - "visualize_states": ppsci.visualize.Visualizer2DPlot( + "visulzie_states": ppsci.visualize.Visualizer2DPlot( vis_datas, { "target_ux": lambda d: d["states"][:, :, 0], diff --git a/examples/darcy/darcy2d.py b/examples/darcy/darcy2d.py index 7f0a3646f..dca5057bb 100644 --- a/examples/darcy/darcy2d.py +++ b/examples/darcy/darcy2d.py @@ -12,26 +12,25 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import numpy as np import paddle -from omegaconf import DictConfig import ppsci from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) + # set output directory + OUTPUT_DIR = "./output_darcy2d" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.MLP(**cfg.MODEL) + model = ppsci.arch.MLP(("x", "y"), ("p",), 5, 20, "stan") # set equation equation = {"Poisson": ppsci.equation.Poisson(2)} @@ -40,11 +39,15 @@ def train(cfg: DictConfig): geom = {"rect": ppsci.geometry.Rectangle((0.0, 0.0), (1.0, 1.0))} # set dataloader config + ITERS_PER_EPOCH = 1 train_dataloader_cfg = { "dataset": "IterableNamedArrayDataset", - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "iters_per_epoch": ITERS_PER_EPOCH, } + NPOINT_PDE = 99**2 + NPOINT_BC = 100 * 4 + # set constraint def poisson_ref_compute_func(_in): return ( @@ -58,7 +61,7 @@ def poisson_ref_compute_func(_in): equation["Poisson"].equations, {"poisson": poisson_ref_compute_func}, geom["rect"], - {**train_dataloader_cfg, "batch_size": cfg.NPOINT_PDE}, + {**train_dataloader_cfg, "batch_size": NPOINT_PDE}, ppsci.loss.MSELoss("sum"), evenly=True, name="EQ", @@ -71,7 +74,7 @@ def poisson_ref_compute_func(_in): * np.cos(2.0 * np.pi * _in["y"]) }, geom["rect"], - {**train_dataloader_cfg, "batch_size": cfg.NPOINT_BC}, + {**train_dataloader_cfg, "batch_size": NPOINT_BC}, ppsci.loss.MSELoss("sum"), name="BC", ) @@ -81,19 +84,28 @@ def poisson_ref_compute_func(_in): bc.name: bc, } + # set training hyper-parameters + EPOCHS = 10000 if not args.epochs else args.epochs + # set optimizer - lr_scheduler = ppsci.optimizer.lr_scheduler.OneCycleLR(**cfg.TRAIN.lr_scheduler)() + lr_scheduler = ppsci.optimizer.lr_scheduler.OneCycleLR( + EPOCHS, + ITERS_PER_EPOCH, + max_learning_rate=1e-3, + end_learning_rate=1e-7, + )() optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) # set validator + NPOINT_EVAL = NPOINT_PDE residual_validator = ppsci.validate.GeometryValidator( equation["Poisson"].equations, {"poisson": poisson_ref_compute_func}, geom["rect"], { "dataset": "NamedArrayDataset", - "total_size": cfg.NPOINT_PDE, - "batch_size": cfg.EVAL.batch_size.residual_validator, + "total_size": NPOINT_EVAL, + "batch_size": 8192, "sampler": {"name": "BatchSampler"}, }, ppsci.loss.MSELoss("sum"), @@ -105,11 +117,9 @@ def poisson_ref_compute_func(_in): # set visualizer(optional) # manually collate input data for visualization, - vis_points = geom["rect"].sample_interior( - cfg.NPOINT_PDE + cfg.NPOINT_BC, evenly=True - ) + vis_points = geom["rect"].sample_interior(NPOINT_PDE + NPOINT_BC, evenly=True) visualizer = { - "visualize_p": ppsci.visualize.VisualizerVtu( + "visulzie_p": ppsci.visualize.VisualizerVtu( vis_points, { "p": lambda d: d["p"], @@ -149,13 +159,13 @@ def poisson_ref_compute_func(_in): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, lr_scheduler, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - eval_freq=cfg.TRAIN.eval_freq, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=200, equation=equation, geom=geom, validator=validator, @@ -168,13 +178,11 @@ def poisson_ref_compute_func(_in): # visualize prediction after finished training solver.visualize() - # fine-tuning pretrained model with L-BFGS - OUTPUT_DIR = cfg.TRAIN.lbfgs.output_dir - logger.init_logger("ppsci", osp.join(OUTPUT_DIR, f"{cfg.mode}.log"), "info") - EPOCHS = cfg.TRAIN.epochs // 10 - optimizer_lbfgs = ppsci.optimizer.LBFGS( - cfg.TRAIN.lbfgs.learning_rate, cfg.TRAIN.lbfgs.max_iter - )(model) + # finetuning pretrained model with L-BFGS + OUTPUT_DIR = "./output_darcy2d_L-BFGS" + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + EPOCHS = EPOCHS // 10 + optimizer_lbfgs = ppsci.optimizer.LBFGS(1.0, max_iter=10)(model) solver = ppsci.solver.Solver( model, constraint, @@ -182,9 +190,9 @@ def poisson_ref_compute_func(_in): optimizer_lbfgs, None, EPOCHS, - cfg.TRAIN.lbfgs.iters_per_epoch, - eval_during_train=cfg.TRAIN.lbfgs.eval_during_train, - eval_freq=cfg.TRAIN.lbfgs.eval_freq, + ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=200, equation=equation, geom=geom, validator=validator, @@ -197,114 +205,18 @@ def poisson_ref_compute_func(_in): # visualize prediction after finished training solver.visualize() - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") - - # set model - model = ppsci.arch.MLP(**cfg.MODEL) - - # set equation - equation = {"Poisson": ppsci.equation.Poisson(2)} - - # set geometry - geom = {"rect": ppsci.geometry.Rectangle((0.0, 0.0), (1.0, 1.0))} - - # set constraint - def poisson_ref_compute_func(_in): - return ( - -8.0 - * (np.pi**2) - * np.sin(2.0 * np.pi * _in["x"]) - * np.cos(2.0 * np.pi * _in["y"]) - ) - - # set validator - residual_validator = ppsci.validate.GeometryValidator( - equation["Poisson"].equations, - {"poisson": poisson_ref_compute_func}, - geom["rect"], - { - "dataset": "NamedArrayDataset", - "total_size": cfg.NPOINT_PDE, - "batch_size": cfg.EVAL.batch_size.residual_validator, - "sampler": {"name": "BatchSampler"}, - }, - ppsci.loss.MSELoss("sum"), - evenly=True, - metric={"MSE": ppsci.metric.MSE()}, - name="Residual", - ) - validator = {residual_validator.name: residual_validator} - - # set visualizer - # manually collate input data for visualization, - vis_points = geom["rect"].sample_interior( - cfg.NPOINT_PDE + cfg.NPOINT_BC, evenly=True - ) - visualizer = { - "visualize_p": ppsci.visualize.VisualizerVtu( - vis_points, - { - "p": lambda d: d["p"], - "p_ref": lambda d: paddle.sin(2 * np.pi * d["x"]) - * paddle.cos(2 * np.pi * d["y"]), - "p_diff": lambda d: paddle.sin(2 * np.pi * d["x"]) - * paddle.cos(2 * np.pi * d["y"]) - - d["p"], - "ux": lambda d: jacobian(d["p"], d["x"]), - "ux_ref": lambda d: 2 - * np.pi - * paddle.cos(2 * np.pi * d["x"]) - * paddle.cos(2 * np.pi * d["y"]), - "ux_diff": lambda d: jacobian(d["p"], d["x"]) - - 2 - * np.pi - * paddle.cos(2 * np.pi * d["x"]) - * paddle.cos(2 * np.pi * d["y"]), - "uy": lambda d: jacobian(d["p"], d["y"]), - "uy_ref": lambda d: -2 - * np.pi - * paddle.sin(2 * np.pi * d["x"]) - * paddle.sin(2 * np.pi * d["y"]), - "uy_diff": lambda d: jacobian(d["p"], d["y"]) - - ( - -2 - * np.pi - * paddle.sin(2 * np.pi * d["x"]) - * paddle.sin(2 * np.pi * d["y"]) - ), - }, - prefix="result_p_ux_uy", - ) - } - + # directly evaluate pretrained model(optional) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") solver = ppsci.solver.Solver( model, - output_dir=cfg.output_dir, + constraint, + OUTPUT_DIR, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - pretrained_model_path=cfg.EVAL.pretrained_model_path, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", ) solver.eval() - # visualize prediction + # visualize prediction for pretrained model(optional) solver.visualize() - - -@hydra.main(version_base=None, config_path="./conf", config_name="darcy2d.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/deephpms/burgers.py b/examples/deephpms/burgers.py index b062ffe77..f1019be17 100644 --- a/examples/deephpms/burgers.py +++ b/examples/deephpms/burgers.py @@ -12,16 +12,13 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import paddle import paddle.nn.functional as F -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger @@ -52,21 +49,26 @@ def boundary_loss_func(output_dict, *args): return losses -def train(cfg: DictConfig): - ppsci.utils.misc.set_random_seed(cfg.seed) +if __name__ == "__main__": + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/DeepHPMs/burgers_sine.mat" + DATASET_PATH_SOL = "./datasets/DeepHPMs/burgers.mat" + OUTPUT_DIR = "./output_burgers/" if args.output_dir is None else args.output_dir + # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # initialize burgers boundaries - t_lb = paddle.to_tensor(cfg.T_LB) - t_ub = paddle.to_tensor(cfg.T_UB) - x_lb = paddle.to_tensor(cfg.X_LB) - x_ub = paddle.to_tensor(cfg.T_UB) + t_lb = paddle.to_tensor([0.0]) + t_ub = paddle.to_tensor([10.0]) + x_lb = paddle.to_tensor([-8.0]) + x_ub = paddle.to_tensor([8.0]) # initialize models - model_idn = ppsci.arch.MLP(**cfg.MODEL.idn_net) - model_pde = ppsci.arch.MLP(**cfg.MODEL.pde_net) - model_sol = ppsci.arch.MLP(**cfg.MODEL.sol_net) + model_idn = ppsci.arch.MLP(("t", "x"), ("u_idn",), 4, 50, "sin") + model_pde = ppsci.arch.MLP(("u_x", "du_x", "du_xx"), ("f_pde",), 2, 100, "sin") + model_sol = ppsci.arch.MLP(("t", "x"), ("u_sol",), 4, 50, "sin") # initialize transform def transform_u(_in): @@ -99,23 +101,28 @@ def transform_f_sol(_in): # initialize model list model_list = ppsci.arch.ModelList((model_idn, model_pde, model_sol)) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 50000 if args.epochs is None else args.epochs # set 1 for LBFGS + # MAX_ITER = 50000 # for LBFGS + # initialize optimizer # Adam - optimizer_idn = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_idn) - optimizer_pde = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_pde) - optimizer_sol = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_sol) + optimizer_idn = ppsci.optimizer.Adam(1e-3)(model_idn) + optimizer_pde = ppsci.optimizer.Adam(1e-3)(model_pde) + optimizer_sol = ppsci.optimizer.Adam(1e-3)(model_sol) # LBFGS - # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_idn, )) - # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_pde, )) - # optimizer_sol = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_sol, )) + # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_idn, )) + # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_pde, )) + # optimizer_sol = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_sol, )) # stage 1: training identification net # manually build constraint(s) train_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_train", "x": "x_train", "u_idn": "u_train"}, @@ -134,7 +141,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_star", "x": "x_star", "u_idn": "u_star"}, @@ -154,12 +161,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_idn, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_idn, ) @@ -173,7 +180,7 @@ def transform_f_sol(_in): train_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_train", "x": "x_train", "du_t": "t_train"}, @@ -195,7 +202,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_star", "x": "x_star", "du_t": "t_star"}, @@ -218,12 +225,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_pde, - cfg.output_dir, + OUTPUT_DIR, optimizer_pde, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_pde, ) @@ -240,7 +247,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_f = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_f_train", "x": "x_f_train", "du_t": "t_f_train"}, @@ -249,7 +256,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_init = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_sol",), "alias_dict": {"t": "t0", "x": "x0", "u_sol": "u0"}, @@ -258,7 +265,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_bc = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("x",), "alias_dict": {"t": "tb", "x": "xb"}, @@ -299,7 +306,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_sol = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_sol",), "alias_dict": {"t": "t_star", "x": "x_star", "u_sol": "u_star"}, @@ -321,12 +328,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_sol, - cfg.output_dir, + OUTPUT_DIR, optimizer_sol, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_sol, ) @@ -334,21 +341,3 @@ def transform_f_sol(_in): solver.train() # evaluate after finished training solver.eval() - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main(version_base=None, config_path="./conf", config_name="burgers.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/deephpms/korteweg_de_vries.py b/examples/deephpms/korteweg_de_vries.py index a9f96a21a..9c24b9281 100644 --- a/examples/deephpms/korteweg_de_vries.py +++ b/examples/deephpms/korteweg_de_vries.py @@ -12,16 +12,13 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import paddle import paddle.nn.functional as F -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger @@ -55,24 +52,31 @@ def boundary_loss_func(output_dict, *args): return losses -def train(cfg: DictConfig): +if __name__ == "__main__": # open FLAG for higher order differential operator when order >= 4 paddle.framework.core.set_prim_eager_enabled(True) + args = config.parse_args() ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/DeepHPMs/KdV_sine.mat" + DATASET_PATH_SOL = "./datasets/DeepHPMs/KdV_cos.mat" + OUTPUT_DIR = "./output_kdv/" if args.output_dir is None else args.output_dir + # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") - # initialize boundaries - t_lb = paddle.to_tensor(cfg.T_LB) - t_ub = paddle.to_tensor(cfg.T_UB) - x_lb = paddle.to_tensor(cfg.X_LB) - x_ub = paddle.to_tensor(cfg.T_UB) + # initialize burgers boundaries + t_lb = paddle.to_tensor([0.0]) + t_ub = paddle.to_tensor([40.0]) + x_lb = paddle.to_tensor([-20.0]) + x_ub = paddle.to_tensor([20.0]) # initialize models - model_idn = ppsci.arch.MLP(**cfg.MODEL.idn_net) - model_pde = ppsci.arch.MLP(**cfg.MODEL.pde_net) - model_sol = ppsci.arch.MLP(**cfg.MODEL.sol_net) + model_idn = ppsci.arch.MLP(("t", "x"), ("u_idn",), 4, 50, "sin") + model_pde = ppsci.arch.MLP( + ("u_x", "du_x", "du_xx", "du_xxx"), ("f_pde",), 2, 100, "sin" + ) + model_sol = ppsci.arch.MLP(("t", "x"), ("u_sol",), 4, 50, "sin") # initialize transform def transform_u(_in): @@ -106,23 +110,28 @@ def transform_f_sol(_in): # initialize model list model_list = ppsci.arch.ModelList((model_idn, model_pde, model_sol)) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 50000 if args.epochs is None else args.epochs # set 1 for LBFGS + # MAX_ITER = 50000 # for LBFGS + # initialize optimizer # Adam - optimizer_idn = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_idn) - optimizer_pde = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_pde) - optimizer_sol = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_sol) + optimizer_idn = ppsci.optimizer.Adam(1e-3)(model_idn) + optimizer_pde = ppsci.optimizer.Adam(1e-3)(model_pde) + optimizer_sol = ppsci.optimizer.Adam(1e-3)(model_sol) # LBFGS - # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_idn, )) - # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_pde, )) - # optimizer_sol = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_sol, )) + # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_idn, )) + # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_pde, )) + # optimizer_sol = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_sol, )) # stage 1: training identification net # manually build constraint(s) train_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_train", "x": "x_train", "u_idn": "u_train"}, @@ -141,7 +150,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_star", "x": "x_star", "u_idn": "u_star"}, @@ -161,12 +170,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_idn, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_idn, ) @@ -180,7 +189,7 @@ def transform_f_sol(_in): train_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_train", "x": "x_train", "du_t": "t_train"}, @@ -202,7 +211,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_star", "x": "x_star", "du_t": "t_star"}, @@ -225,12 +234,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_pde, - cfg.output_dir, + OUTPUT_DIR, optimizer_pde, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_pde, ) @@ -247,7 +256,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_f = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_f_train", "x": "x_f_train", "du_t": "t_f_train"}, @@ -256,7 +265,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_init = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_sol",), "alias_dict": {"t": "t0", "x": "x0", "u_sol": "u0"}, @@ -265,7 +274,7 @@ def transform_f_sol(_in): train_dataloader_cfg_sol_bc = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("x",), "alias_dict": {"t": "tb", "x": "xb"}, @@ -306,7 +315,7 @@ def transform_f_sol(_in): eval_dataloader_cfg_sol = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_sol",), "alias_dict": {"t": "t_star", "x": "x_star", "u_sol": "u_star"}, @@ -328,12 +337,12 @@ def transform_f_sol(_in): solver = ppsci.solver.Solver( model_list, constraint_sol, - cfg.output_dir, + OUTPUT_DIR, optimizer_sol, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_sol, ) @@ -341,23 +350,3 @@ def transform_f_sol(_in): solver.train() # evaluate after finished training solver.eval() - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main( - version_base=None, config_path="./conf", config_name="korteweg_de_vries.yaml" -) -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/deephpms/kuramoto_sivashinsky.py b/examples/deephpms/kuramoto_sivashinsky.py index 9b6ca9f10..e21cc2235 100644 --- a/examples/deephpms/kuramoto_sivashinsky.py +++ b/examples/deephpms/kuramoto_sivashinsky.py @@ -12,16 +12,13 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import paddle import paddle.nn.functional as F -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger @@ -58,19 +55,24 @@ def boundary_loss_func(output_dict, *args): return losses -def train(cfg: DictConfig): +if __name__ == "__main__": # open FLAG for higher order differential operator when order >= 4 paddle.framework.core.set_prim_eager_enabled(True) - ppsci.utils.misc.set_random_seed(cfg.seed) + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/DeepHPMs/KS.mat" + DATASET_PATH_SOL = "./datasets/DeepHPMs/KS.mat" + OUTPUT_DIR = "./output_ks/" if args.output_dir is None else args.output_dir + # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") - # initialize boundaries - t_lb = paddle.to_tensor(cfg.T_LB) - t_ub = paddle.to_tensor(cfg.T_UB) - x_lb = paddle.to_tensor(cfg.X_LB) - x_ub = paddle.to_tensor(cfg.T_UB) + # initialize burgers boundaries + t_lb = paddle.to_tensor([0.0]) + t_ub = paddle.to_tensor([50.0]) + x_lb = paddle.to_tensor([-10.0]) + x_ub = paddle.to_tensor([10.0]) # boundaries of KS_chaotic.mat # t_lb = paddle.to_tensor([0.0]) @@ -79,8 +81,14 @@ def train(cfg: DictConfig): # x_ub = paddle.to_tensor([32.0 * np.pi]) # initialize models - model_idn = ppsci.arch.MLP(**cfg.MODEL.idn_net) - model_pde = ppsci.arch.MLP(**cfg.MODEL.pde_net) + model_idn = ppsci.arch.MLP(("t", "x"), ("u_idn",), 4, 50, "sin") + model_pde = ppsci.arch.MLP( + ("u_x", "du_x", "du_xx", "du_xxx", "du_xxxx"), + ("f_pde",), + 2, + 100, + "sin", + ) # initialize transform def transform_u(_in): @@ -117,21 +125,26 @@ def transform_f_idn(_in): # initialize model list model_list = ppsci.arch.ModelList((model_idn, model_pde)) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 50000 if args.epochs is None else args.epochs # set 1 for LBFGS + # MAX_ITER = 50000 # for LBFGS + # initialize optimizer # Adam - optimizer_idn = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_idn) - optimizer_pde = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_pde) + optimizer_idn = ppsci.optimizer.Adam(1e-4)(model_idn) + optimizer_pde = ppsci.optimizer.Adam(1e-4)(model_pde) # LBFGS - # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_idn, )) - # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_pde, )) + # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_idn, )) + # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_pde, )) # stage 1: training identification net # manually build constraint(s) train_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_train", "x": "x_train", "u_idn": "u_train"}, @@ -150,7 +163,7 @@ def transform_f_idn(_in): eval_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn",), "alias_dict": {"t": "t_star", "x": "x_star", "u_idn": "u_star"}, @@ -170,12 +183,12 @@ def transform_f_idn(_in): solver = ppsci.solver.Solver( model_list, constraint_idn, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_idn, ) @@ -189,7 +202,7 @@ def transform_f_idn(_in): train_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_train", "x": "x_train", "du_t": "t_train"}, @@ -211,7 +224,7 @@ def transform_f_idn(_in): eval_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_star", "x": "x_star", "du_t": "t_star"}, @@ -234,12 +247,12 @@ def transform_f_idn(_in): solver = ppsci.solver.Solver( model_list, constraint_pde, - cfg.output_dir, + OUTPUT_DIR, optimizer_pde, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_pde, ) @@ -253,7 +266,7 @@ def transform_f_idn(_in): train_dataloader_cfg_sol_f = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("du_t",), "alias_dict": {"t": "t_f_train", "x": "x_f_train", "du_t": "t_f_train"}, @@ -262,7 +275,7 @@ def transform_f_idn(_in): train_dataloader_cfg_sol_init = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u0_sol",), "alias_dict": {"t": "t0", "x": "x0", "u0_sol": "u0"}, @@ -271,7 +284,7 @@ def transform_f_idn(_in): train_dataloader_cfg_sol_bc = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("x",), "alias_dict": {"t": "tb", "x": "xb"}, @@ -312,7 +325,7 @@ def transform_f_idn(_in): eval_dataloader_cfg_sol = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_sol",), "alias_dict": {"t": "t_star", "x": "x_star", "u_sol": "u_star"}, @@ -334,12 +347,12 @@ def transform_f_idn(_in): solver = ppsci.solver.Solver( model_list, constraint_sol, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_sol, ) @@ -347,23 +360,3 @@ def transform_f_idn(_in): solver.train() # evaluate after finished training solver.eval() - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main( - version_base=None, config_path="./conf", config_name="kuramoto_sivashinsky.yaml" -) -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/deephpms/navier_stokes.py b/examples/deephpms/navier_stokes.py index b9e7139c3..e69cc2833 100644 --- a/examples/deephpms/navier_stokes.py +++ b/examples/deephpms/navier_stokes.py @@ -12,16 +12,13 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import paddle import paddle.nn.functional as F -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger @@ -38,19 +35,30 @@ def pde_l2_rel_func(output_dict, *args): return metric_dict -def train(cfg: DictConfig): - ppsci.utils.misc.set_random_seed(cfg.seed) +if __name__ == "__main__": + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/DeepHPMs/cylinder.mat" + DATASET_PATH_SOL = "./datasets/DeepHPMs/cylinder.mat" + OUTPUT_DIR = "./output_ns/" if args.output_dir is None else args.output_dir + # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") - # initialize boundaries + # initialize burgers boundaries # t, x, y - lb = paddle.to_tensor(list(cfg.LB)) - ub = paddle.to_tensor(list(cfg.UB)) + lb = paddle.to_tensor([0.0, 1, -1.7]) + ub = paddle.to_tensor([30.0, 7.5, 1.7]) # initialize models - model_idn = ppsci.arch.MLP(**cfg.MODEL.idn_net) - model_pde = ppsci.arch.MLP(**cfg.MODEL.pde_net) + model_idn = ppsci.arch.MLP(("t", "x", "y"), ("w_idn",), 4, 200, "sin") + model_pde = ppsci.arch.MLP( + ("u", "v", "w", "dw_x", "dw_y", "dw_xx", "dw_xy", "dw_yy"), + ("f_pde",), + 2, + 100, + "sin", + ) # initialize transform def transform_w(_in): @@ -91,21 +99,27 @@ def transform_f(_in): # initialize model list model_list = ppsci.arch.ModelList((model_idn, model_pde)) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 50000 if args.epochs is None else args.epochs # set 1 for LBFGS + # MAX_ITER = 50000 # for LBFGS + EVAL_BATCH_SIZE = 10000 + # initialize optimizer # Adam - optimizer_idn = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_idn) - optimizer_pde = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model_pde) + optimizer_idn = ppsci.optimizer.Adam(1e-4)(model_idn) + optimizer_pde = ppsci.optimizer.Adam(1e-4)(model_pde) # LBFGS - # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_idn, )) - # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_pde, )) + # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_idn,)) + # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_pde,)) # stage 1: training identification net # manually build constraint(s) train_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("w_idn",), "alias_dict": { @@ -131,7 +145,7 @@ def transform_f(_in): eval_dataloader_cfg_idn = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("w_idn",), "alias_dict": { @@ -143,7 +157,7 @@ def transform_f(_in): "w_idn": "w_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -164,12 +178,12 @@ def transform_f(_in): solver = ppsci.solver.Solver( model_list, constraint_idn, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_idn, ) @@ -183,7 +197,7 @@ def transform_f(_in): train_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("dw_t",), "alias_dict": { @@ -212,7 +226,7 @@ def transform_f(_in): eval_dataloader_cfg_pde = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("dw_t",), "alias_dict": { @@ -224,7 +238,7 @@ def transform_f(_in): "dw_t": "t_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -248,12 +262,12 @@ def transform_f(_in): solver = ppsci.solver.Solver( model_list, constraint_pde, - cfg.output_dir, + OUTPUT_DIR, optimizer_pde, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_pde, ) @@ -267,7 +281,7 @@ def transform_f(_in): train_dataloader_cfg_sol_f = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("dw_t",), "alias_dict": { @@ -283,7 +297,7 @@ def transform_f(_in): train_dataloader_cfg_sol_bc = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("wb_sol",), "alias_dict": { @@ -321,7 +335,7 @@ def transform_f(_in): eval_dataloader_cfg_sol = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x", "y", "u", "v"), "label_keys": ("w_sol",), "alias_dict": { @@ -333,7 +347,7 @@ def transform_f(_in): "v": "v_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -356,12 +370,12 @@ def transform_f(_in): solver = ppsci.solver.Solver( model_list, constraint_sol, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_sol, ) @@ -369,21 +383,3 @@ def transform_f(_in): solver.train() # evaluate after finished training solver.eval() - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main(version_base=None, config_path="./conf", config_name="navier_stokes.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/deephpms/schrodinger.py b/examples/deephpms/schrodinger.py index 8a3944512..4f1eb32e4 100644 --- a/examples/deephpms/schrodinger.py +++ b/examples/deephpms/schrodinger.py @@ -12,17 +12,14 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra import numpy as np import paddle import paddle.nn.functional as F -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger @@ -70,22 +67,39 @@ def sol_l2_rel_func(output_dict, label_dict): return metric_dict -def train(cfg: DictConfig): - ppsci.utils.misc.set_random_seed(cfg.seed) +if __name__ == "__main__": + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/DeepHPMs/NLS.mat" + DATASET_PATH_SOL = "./datasets/DeepHPMs/NLS.mat" + OUTPUT_DIR = "./output_schrodinger/" if args.output_dir is None else args.output_dir + # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # initialize boundaries - t_lb = paddle.to_tensor(cfg.T_LB) - t_ub = paddle.to_tensor(np.pi / cfg.T_UB) - x_lb = paddle.to_tensor(cfg.X_LB) - x_ub = paddle.to_tensor(cfg.X_UB) + t_lb = paddle.to_tensor([0.0]) + t_ub = paddle.to_tensor([np.pi / 2.0]) + x_lb = paddle.to_tensor([-5.0]) + x_ub = paddle.to_tensor([5.0]) # initialize models - model_idn_u = ppsci.arch.MLP(**cfg.MODEL.idn_u_net) - model_idn_v = ppsci.arch.MLP(**cfg.MODEL.idn_v_net) - model_pde_f = ppsci.arch.MLP(**cfg.MODEL.pde_f_net) - model_pde_g = ppsci.arch.MLP(**cfg.MODEL.pde_g_net) + model_idn_u = ppsci.arch.MLP(("t", "x"), ("u_idn",), 4, 50, "sin") + model_idn_v = ppsci.arch.MLP(("t", "x"), ("v_idn",), 4, 50, "sin") + model_pde_f = ppsci.arch.MLP( + ("u", "v", "du_x", "dv_x", "du_xx", "dv_xx"), + ("f_pde",), + 2, + 100, + "sin", + ) + model_pde_g = ppsci.arch.MLP( + ("u", "v", "du_x", "dv_x", "du_xx", "dv_xx"), + ("g_pde",), + 2, + 100, + "sin", + ) # initialize transform def transform_uv(_in): @@ -128,25 +142,27 @@ def transform_fg(_in): (model_idn_u, model_idn_v, model_pde_f, model_pde_g) ) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 50000 if args.epochs is None else args.epochs # set 1 for LBFGS + # MAX_ITER = 50000 # for LBFGS + EVAL_BATCH_SIZE = 10000 + # initialize optimizer # Adam - optimizer_idn = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)( - (model_idn_u, model_idn_v) - ) - optimizer_pde = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)( - (model_pde_f, model_pde_g) - ) + optimizer_idn = ppsci.optimizer.Adam(1e-4)((model_idn_u, model_idn_v)) + optimizer_pde = ppsci.optimizer.Adam(1e-4)((model_pde_f, model_pde_g)) # LBFGS - # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_idn_u, model_idn_v)) - # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)((model_pde_f, model_pde_g)) + # optimizer_idn = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_idn_u, model_idn_v)) + # optimizer_pde = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)((model_pde_f, model_pde_g)) # stage 1: training identification net # manually build constraint(s) train_dataloader_cfg_idn = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn", "v_idn"), "alias_dict": { @@ -170,7 +186,7 @@ def transform_fg(_in): eval_dataloader_cfg_idn = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("u_idn", "v_idn"), "alias_dict": { @@ -180,7 +196,7 @@ def transform_fg(_in): "v_idn": "v_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -201,12 +217,12 @@ def transform_fg(_in): solver = ppsci.solver.Solver( model_list, constraint_idn, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_idn, ) @@ -220,7 +236,7 @@ def transform_fg(_in): train_dataloader_cfg_pde = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t", "dv_t"), "alias_dict": { @@ -249,7 +265,7 @@ def transform_fg(_in): eval_dataloader_cfg_pde = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("t", "x"), "label_keys": ("du_t", "dv_t"), "alias_dict": { @@ -259,7 +275,7 @@ def transform_fg(_in): "dv_t": "t_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -285,12 +301,12 @@ def transform_fg(_in): solver = ppsci.solver.Solver( model_list, constraint_pde, - cfg.output_dir, + OUTPUT_DIR, optimizer_pde, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_pde, ) @@ -308,7 +324,7 @@ def transform_fg(_in): train_dataloader_cfg_sol_f = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("du_t", "dv_t"), "alias_dict": { @@ -322,7 +338,7 @@ def transform_fg(_in): train_dataloader_cfg_sol_init = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_idn", "v_idn"), "alias_dict": {"t": "t0", "x": "x0", "u_idn": "u0", "v_idn": "v0"}, @@ -331,7 +347,7 @@ def transform_fg(_in): train_dataloader_cfg_sol_bc = { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("x",), "alias_dict": {"t": "tb", "x": "xb"}, @@ -375,7 +391,7 @@ def transform_fg(_in): eval_dataloader_cfg_sol = { "dataset": { "name": "MatDataset", - "file_path": cfg.DATASET_PATH_SOL, + "file_path": DATASET_PATH_SOL, "input_keys": ("t", "x"), "label_keys": ("u_idn", "v_idn"), "alias_dict": { @@ -385,7 +401,7 @@ def transform_fg(_in): "v_idn": "v_star", }, }, - "batch_size": cfg.TRAIN.batch_size.eval, + "batch_size": EVAL_BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -408,12 +424,12 @@ def transform_fg(_in): solver = ppsci.solver.Solver( model_list, constraint_sol, - cfg.output_dir, + OUTPUT_DIR, optimizer_idn, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator_sol, ) @@ -421,21 +437,3 @@ def transform_fg(_in): solver.train() # evaluate after finished training solver.eval() - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main(version_base=None, config_path="./conf", config_name="schrodinger.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/euler_beam/euler_beam.py b/examples/euler_beam/euler_beam.py index c16d4cc7e..1dfffeaec 100644 --- a/examples/euler_beam/euler_beam.py +++ b/examples/euler_beam/euler_beam.py @@ -108,7 +108,7 @@ def u_solution_func(out): # set visualizer(optional) visu_points = geom["interval"].sample_interior(TOTAL_SIZE, evenly=True) visualizer = { - "visualize_u": ppsci.visualize.VisualizerScatter1D( + "visulzie_u": ppsci.visualize.VisualizerScatter1D( visu_points, ("x",), {"u": lambda d: d["u"]}, diff --git a/examples/fourcastnet/train_finetune.py b/examples/fourcastnet/train_finetune.py index 11d809e46..370f08995 100644 --- a/examples/fourcastnet/train_finetune.py +++ b/examples/fourcastnet/train_finetune.py @@ -26,7 +26,7 @@ from ppsci.utils import logger -def get_vis_data( +def get_vis_datas( file_path: str, date_strings: Tuple[str, ...], num_timestamps: int, @@ -43,15 +43,15 @@ def get_vis_data( data.append(_file[ic : ic + num_timestamps + 1, vars_channel, 0:img_h]) data = np.asarray(data) - vis_data = {"input": (data[:, 0] - data_mean) / data_std} + vis_datas = {"input": (data[:, 0] - data_mean) / data_std} for t in range(num_timestamps): hour = (t + 1) * 6 data_t = data[:, t + 1] wind_data = [] for i in range(data_t.shape[0]): wind_data.append((data_t[i][0] ** 2 + data_t[i][1] ** 2) ** 0.5) - vis_data[f"target_{hour}h"] = np.asarray(wind_data) - return vis_data + vis_datas[f"target_{hour}h"] = np.asarray(wind_data) + return vis_datas if __name__ == "__main__": @@ -155,7 +155,7 @@ def get_vis_data( "batch_size": 1, } - # set metric + # set metirc metric = { "MAE": ppsci.metric.MAE(keep_batch=True), "LatitudeWeightedRMSE": ppsci.metric.LatitudeWeightedRMSE( @@ -239,9 +239,9 @@ def get_vis_data( ) validator = {sup_validator.name: sup_validator} - # set visualizer data + # set visualizer datas DATE_STRINGS = ("2018-09-08 00:00:00",) - vis_data = get_vis_data( + vis_datas = get_vis_datas( TEST_FILE_PATH, DATE_STRINGS, NUM_TIMESTAMPS, @@ -270,8 +270,8 @@ def output_wind_func(d, var_name, data_mean, data_std): vis_output_expr[f"target_{hour}h"] = lambda d, hour=hour: d[f"target_{hour}h"] # set visualizer visualizer = { - "visualize_wind": ppsci.visualize.VisualizerWeather( - vis_data, + "visulize_wind": ppsci.visualize.VisualizerWeather( + vis_datas, vis_output_expr, xticks=np.linspace(0, 1439, 13), xticklabels=[str(i) for i in range(360, -1, -30)], diff --git a/examples/fourcastnet/train_precip.py b/examples/fourcastnet/train_precip.py index 6f3549443..998516457 100644 --- a/examples/fourcastnet/train_precip.py +++ b/examples/fourcastnet/train_precip.py @@ -26,7 +26,7 @@ from ppsci.utils import logger -def get_vis_data( +def get_vis_datas( wind_file_path: str, file_path: str, date_strings: Tuple[str, ...], @@ -48,12 +48,12 @@ def get_vis_data( wind_data = np.asarray(wind_data) data = np.asarray(data) - vis_data = {"input": (wind_data - data_mean) / data_std} + vis_datas = {"input": (wind_data - data_mean) / data_std} for t in range(num_timestamps): hour = (t + 1) * 6 data_t = data[:, t] - vis_data[f"target_{hour}h"] = np.asarray(data_t) - return vis_data + vis_datas[f"target_{hour}h"] = np.asarray(data_t) + return vis_datas if __name__ == "__main__": @@ -164,7 +164,7 @@ def get_vis_data( "batch_size": 1, } - # set metric + # set metirc metric = { "MAE": ppsci.metric.MAE(keep_batch=True), "LatitudeWeightedRMSE": ppsci.metric.LatitudeWeightedRMSE( @@ -246,9 +246,9 @@ def get_vis_data( ) validator = {sup_validator.name: sup_validator} - # set set visualizer data + # set set visualizer datas DATE_STRINGS = ("2018-04-04 00:00:00",) - vis_data = get_vis_data( + vis_datas = get_vis_datas( WIND_TEST_FILE_PATH, TEST_FILE_PATH, DATE_STRINGS, @@ -275,8 +275,8 @@ def output_precip_func(d, var_name): ) # set visualizer visualizer = { - "visualize_precip": ppsci.visualize.VisualizerWeather( - vis_data, + "visulize_precip": ppsci.visualize.VisualizerWeather( + vis_datas, visu_output_expr, xticks=np.linspace(0, 1439, 13), xticklabels=[str(i) for i in range(360, -1, -30)], diff --git a/examples/fpde/fractional_poisson_2d.py b/examples/fpde/fractional_poisson_2d.py index 6acb518f5..3b8d74f2c 100644 --- a/examples/fpde/fractional_poisson_2d.py +++ b/examples/fpde/fractional_poisson_2d.py @@ -16,7 +16,6 @@ import math from typing import Dict -from typing import Tuple from typing import Union import numpy as np @@ -69,35 +68,22 @@ def u_solution_func( return paddle.abs(1 - (out["x"] ** 2 + out["y"] ** 2)) ** (1 + ALPHA / 2) return np.abs(1 - (out["x"] ** 2 + out["y"] ** 2)) ** (1 + ALPHA / 2) - # set transform for input data - def input_data_fpde_transform( - input: Dict[str, np.ndarray], - weight: Dict[str, np.ndarray], - label: Dict[str, np.ndarray], - ) -> Tuple[ - Dict[str, paddle.Tensor], Dict[str, paddle.Tensor], Dict[str, paddle.Tensor] - ]: + # set input transform + def fpde_transform(in_: Dict[str, np.ndarray]) -> Dict[str, np.ndarray]: """Get sampling points for integral. Args: - input (Dict[str, paddle.Tensor]): Raw input dict. - weight (Dict[str, paddle.Tensor]): Raw weight dict. - label (Dict[str, paddle.Tensor]): Raw label dict. + in_ (Dict[str, np.ndarray]): Raw input dict. Returns: - Tuple[ Dict[str, paddle.Tensor], Dict[str, paddle.Tensor], Dict[str, paddle.Tensor] ]: - Input dict contained sampling points, weight dict and label dict. + Dict[str, np.ndarray]: Input dict contained sampling points. """ - points = np.concatenate((input["x"].numpy(), input["y"].numpy()), axis=1) + points = np.concatenate((in_["x"].numpy(), in_["y"].numpy()), axis=1) x = equation["fpde"].get_x(points) - return ( - { - **input, - **{k: paddle.to_tensor(v) for k, v in x.items()}, - }, - weight, - label, - ) + return { + **in_, + **{k: paddle.to_tensor(v) for k, v in x.items()}, + } fpde_constraint = ppsci.constraint.InteriorConstraint( equation["fpde"].equations, @@ -109,7 +95,7 @@ def input_data_fpde_transform( "transforms": ( { "FunctionalTransform": { - "transform_func": input_data_fpde_transform, + "transform_func": fpde_transform, }, }, ), diff --git a/examples/fsi/viv.py b/examples/fsi/viv.py index 90f4ad1e8..9a23d382d 100644 --- a/examples/fsi/viv.py +++ b/examples/fsi/viv.py @@ -71,7 +71,7 @@ optimizer = ppsci.optimizer.Adam(lr_scheduler)((model,) + tuple(equation.values())) # set validator - valid_dataloader_cfg = { + valida_dataloader_cfg = { "dataset": { "name": "MatDataset", "file_path": "./VIV_Training_Neta100.mat", @@ -86,7 +86,7 @@ }, } eta_mse_validator = ppsci.validate.SupervisedValidator( - valid_dataloader_cfg, + valida_dataloader_cfg, ppsci.loss.MSELoss("mean"), {"eta": lambda out: out["eta"], **equation["VIV"].equations}, metric={"MSE": ppsci.metric.MSE()}, @@ -101,7 +101,7 @@ alias_dict={"eta_gt": "eta", "f_gt": "f"}, ) visualizer = { - "visualize_u": ppsci.visualize.VisualizerScatter1D( + "visulzie_u": ppsci.visualize.VisualizerScatter1D( visu_mat, ("t_f",), { diff --git a/examples/hpinns/functions.py b/examples/hpinns/functions.py index 8583f1d11..1cad22568 100644 --- a/examples/hpinns/functions.py +++ b/examples/hpinns/functions.py @@ -297,7 +297,7 @@ def obj_loss_fun(output_dict: Dict[str, paddle.Tensor], *args) -> paddle.Tensor: def eval_loss_fun(output_dict: Dict[str, paddle.Tensor], *args) -> paddle.Tensor: - """Compute objective loss for evaluation. + """Compute objective loss for evalution. Args: output_dict (Dict[str, paddle.Tensor]): Dict of outputs contains tensor. diff --git a/examples/hpinns/holography.py b/examples/hpinns/holography.py index 5309ef8da..f7dcc2f1b 100644 --- a/examples/hpinns/holography.py +++ b/examples/hpinns/holography.py @@ -16,35 +16,44 @@ This module is heavily adapted from https://github.com/lululxvi/hpinn """ -from os import path as osp - import functions as func_module -import hydra import numpy as np import paddle import plotting as plot_module -from omegaconf import DictConfig import ppsci from ppsci.autodiff import hessian from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": # open FLAG for higher order differential operator paddle.framework.core.set_prim_eager_enabled(True) - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") - - model_re = ppsci.arch.MLP(**cfg.MODEL.re_net) - model_im = ppsci.arch.MLP(**cfg.MODEL.im_net) - model_eps = ppsci.arch.MLP(**cfg.MODEL.eps_net) + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/hpinns_holo_train.mat" + DATASET_PATH_VALID = "./datasets/hpinns_holo_valid.mat" + OUTPUT_DIR = "./output_hpinns/" if args.output_dir is None else args.output_dir - # initialize params - func_module.train_mode = cfg.TRAIN_MODE + # initialize logger + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + # initialize models + in_keys = () + for t in range(1, 7): + in_keys += (f"x_cos_{t}", f"x_sin_{t}") + in_keys += ("y", "y_cos_1", "y_sin_1") + + model_re = ppsci.arch.MLP(in_keys, ("e_re",), 4, 48, "tanh") + model_im = ppsci.arch.MLP(in_keys, ("e_im",), 4, 48, "tanh") + model_eps = ppsci.arch.MLP(in_keys, ("eps",), 4, 48, "tanh") + + # intialize params + train_mode = "aug_lag" # "soft", "penalty", "aug_lag" + k = 9 + func_module.train_mode = train_mode loss_log_obj = [] # register transform @@ -58,10 +67,12 @@ def train(cfg: DictConfig): model_list = ppsci.arch.ModelList((model_re, model_im, model_eps)) + # set training hyper-parameters + ITERS_PER_EPOCH = 1 + EPOCHS = 20000 if args.epochs is None else args.epochs + # initialize Adam optimizer - optimizer_adam = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)( - (model_re, model_im, model_eps) - ) + optimizer_adam = ppsci.optimizer.Adam(1e-3)((model_re, model_im, model_eps)) # manually build constraint(s) label_keys = ("x", "y", "bound", "e_real", "e_imaginary", "epsilon") @@ -96,7 +107,7 @@ def train(cfg: DictConfig): { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("x", "y", "bound"), "label_keys": label_keys + label_keys_derivative, "alias_dict": { @@ -115,7 +126,7 @@ def train(cfg: DictConfig): { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH, + "file_path": DATASET_PATH, "input_keys": ("x", "y", "bound"), "label_keys": label_keys, "alias_dict": {"e_real": "x", "e_imaginary": "x", "epsilon": "x"}, @@ -135,7 +146,7 @@ def train(cfg: DictConfig): { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_VALID, + "file_path": DATASET_PATH_VALID, "input_keys": ("x", "y", "bound"), "label_keys": label_keys + label_keys_derivative, "alias_dict": { @@ -157,7 +168,7 @@ def train(cfg: DictConfig): { "dataset": { "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_VALID, + "file_path": DATASET_PATH_VALID, "input_keys": ("x", "y", "bound"), "label_keys": label_keys + label_keys_derivative, "alias_dict": { @@ -184,14 +195,13 @@ def train(cfg: DictConfig): solver = ppsci.solver.Solver( model_list, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer_adam, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator, - checkpoint_path=cfg.TRAIN.checkpoint_path, ) # train model @@ -199,24 +209,27 @@ def train(cfg: DictConfig): # evaluate after finished training solver.eval() + # set training hyper-parameters + EPOCHS_LBFGS = 1 + MAX_ITER = 15000 + # initialize LBFGS optimizer - optimizer_lbfgs = ppsci.optimizer.LBFGS(max_iter=cfg.TRAIN.max_iter)( + optimizer_lbfgs = ppsci.optimizer.LBFGS(max_iter=MAX_ITER)( (model_re, model_im, model_eps) ) # train: soft constraint, epoch=1 for lbfgs - if cfg.TRAIN_MODE == "soft": + if train_mode == "soft": solver = ppsci.solver.Solver( model_list, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer_lbfgs, None, - cfg.TRAIN.epochs_lbfgs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS_LBFGS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator, - checkpoint_path=cfg.TRAIN.checkpoint_path, ) # train model @@ -228,10 +241,8 @@ def train(cfg: DictConfig): loss_log_obj.append(func_module.loss_obj) # penalty and augmented Lagrangian, difference between the two is updating of lambda - if cfg.TRAIN_MODE != "soft": - train_dict = ppsci.utils.reader.load_mat_file( - cfg.DATASET_PATH, ("x", "y", "bound") - ) + if train_mode != "soft": + train_dict = ppsci.utils.reader.load_mat_file(DATASET_PATH, ("x", "y", "bound")) in_dict = {"x": train_dict["x"], "y": train_dict["y"]} expr_dict = output_expr.copy() expr_dict.pop("bound") @@ -244,7 +255,7 @@ def train(cfg: DictConfig): ] ) - for i in range(1, cfg.TRAIN_K + 1): + for i in range(1, k + 1): pred_dict = solver.predict( in_dict, expr_dict, @@ -259,14 +270,13 @@ def train(cfg: DictConfig): solver = ppsci.solver.Solver( model_list, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer_lbfgs, None, - cfg.TRAIN.epochs_lbfgs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, + EPOCHS_LBFGS, + ITERS_PER_EPOCH, + eval_during_train=False, validator=validator, - checkpoint_path=cfg.TRAIN.checkpoint_path, ) # train model @@ -280,144 +290,11 @@ def train(cfg: DictConfig): # log of loss loss_log = np.array(func_module.loss_log).reshape(-1, 3) - plot_module.set_params( - cfg.TRAIN_MODE, cfg.output_dir, cfg.DATASET_PATH, cfg.DATASET_PATH_VALID - ) + plot_module.set_params(train_mode, OUTPUT_DIR, DATASET_PATH, DATASET_PATH_VALID) plot_module.plot_6a(loss_log) - if cfg.TRAIN_MODE != "soft": + if train_mode != "soft": plot_module.prepare_data(solver, expr_dict) plot_module.plot_6b(loss_log_obj) plot_module.plot_6c7c(func_module.lambda_log) plot_module.plot_6d(func_module.lambda_log) plot_module.plot_6ef(func_module.lambda_log) - - -def evaluate(cfg: DictConfig): - # open FLAG for higher order differential operator - paddle.framework.core.set_prim_eager_enabled(True) - - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") - - model_re = ppsci.arch.MLP(**cfg.MODEL.re_net) - model_im = ppsci.arch.MLP(**cfg.MODEL.im_net) - model_eps = ppsci.arch.MLP(**cfg.MODEL.eps_net) - - # initialize params - func_module.train_mode = cfg.TRAIN_MODE - - # register transform - model_re.register_input_transform(func_module.transform_in) - model_im.register_input_transform(func_module.transform_in) - model_eps.register_input_transform(func_module.transform_in) - - model_re.register_output_transform(func_module.transform_out_real_part) - model_im.register_output_transform(func_module.transform_out_imaginary_part) - model_eps.register_output_transform(func_module.transform_out_epsilon) - - model_list = ppsci.arch.ModelList((model_re, model_im, model_eps)) - - # manually build constraint(s) - label_keys = ("x", "y", "bound", "e_real", "e_imaginary", "epsilon") - label_keys_derivative = ( - "de_re_x", - "de_re_y", - "de_re_xx", - "de_re_yy", - "de_im_x", - "de_im_y", - "de_im_xx", - "de_im_yy", - ) - output_expr = { - "x": lambda out: out["x"], - "y": lambda out: out["y"], - "bound": lambda out: out["bound"], - "e_real": lambda out: out["e_real"], - "e_imaginary": lambda out: out["e_imaginary"], - "epsilon": lambda out: out["epsilon"], - "de_re_x": lambda out: jacobian(out["e_real"], out["x"]), - "de_re_y": lambda out: jacobian(out["e_real"], out["y"]), - "de_re_xx": lambda out: hessian(out["e_real"], out["x"]), - "de_re_yy": lambda out: hessian(out["e_real"], out["y"]), - "de_im_x": lambda out: jacobian(out["e_imaginary"], out["x"]), - "de_im_y": lambda out: jacobian(out["e_imaginary"], out["y"]), - "de_im_xx": lambda out: hessian(out["e_imaginary"], out["x"]), - "de_im_yy": lambda out: hessian(out["e_imaginary"], out["y"]), - } - - # manually build validator - sup_validator_opt = ppsci.validate.SupervisedValidator( - { - "dataset": { - "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_VALID, - "input_keys": ("x", "y", "bound"), - "label_keys": label_keys + label_keys_derivative, - "alias_dict": { - "x": "x_opt", - "y": "y_opt", - "e_real": "x_opt", - "e_imaginary": "x_opt", - "epsilon": "x_opt", - **{k: "x_opt" for k in label_keys_derivative}, - }, - }, - }, - ppsci.loss.FunctionalLoss(func_module.eval_loss_fun), - output_expr, - {"mse": ppsci.metric.FunctionalMetric(func_module.eval_metric_fun)}, - name="opt_sup", - ) - sup_validator_val = ppsci.validate.SupervisedValidator( - { - "dataset": { - "name": "IterableMatDataset", - "file_path": cfg.DATASET_PATH_VALID, - "input_keys": ("x", "y", "bound"), - "label_keys": label_keys + label_keys_derivative, - "alias_dict": { - "x": "x_val", - "y": "y_val", - "e_real": "x_val", - "e_imaginary": "x_val", - "epsilon": "x_val", - **{k: "x_val" for k in label_keys_derivative}, - }, - }, - }, - ppsci.loss.FunctionalLoss(func_module.eval_loss_fun), - output_expr, - {"mse": ppsci.metric.FunctionalMetric(func_module.eval_metric_fun)}, - name="val_sup", - ) - validator = { - sup_validator_opt.name: sup_validator_opt, - sup_validator_val.name: sup_validator_val, - } - - solver = ppsci.solver.Solver( - model_list, - output_dir=cfg.output_dir, - seed=cfg.seed, - validator=validator, - pretrained_model_path=cfg.EVAL.pretrained_model_path, - ) - - # evaluate after finished training - solver.eval() - - -@hydra.main(version_base=None, config_path="./conf", config_name="hpinns.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/hpinns/plotting.py b/examples/hpinns/plotting.py index 9cd0c8a09..8c4d6fded 100644 --- a/examples/hpinns/plotting.py +++ b/examples/hpinns/plotting.py @@ -117,7 +117,7 @@ def plot_field_holo( coord_lambda: np.ndarray, field_lambda: np.ndarray, ): - """Plot fields of of holography example. + """Plot fields of of holograpy example. Args: coord_visual (np.ndarray): The coord of epsilon and |E|**2. diff --git a/examples/ide/volterra_ide.py b/examples/ide/volterra_ide.py index 5601ea9aa..c11dd1619 100644 --- a/examples/ide/volterra_ide.py +++ b/examples/ide/volterra_ide.py @@ -14,35 +14,38 @@ # Reference: https://github.com/lululxvi/deepxde/blob/master/examples/pinn_forward/Volterra_IDE.py -from os import path as osp from typing import Dict -from typing import Tuple -import hydra import numpy as np import paddle from matplotlib import pyplot as plt -from omegaconf import DictConfig import ppsci from ppsci.autodiff import jacobian +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) # set output directory - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + OUTPUT_DIR = "./output_Volterra_IDE" if not args.output_dir else args.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.MLP(**cfg.MODEL) + model = ppsci.arch.MLP(("x",), ("u",), 3, 20) # set geometry - geom = {"timedomain": ppsci.geometry.TimeDomain(*cfg.BOUNDS)} + BOUNDS = (0, 5) + geom = {"timedomain": ppsci.geometry.TimeDomain(BOUNDS[0], BOUNDS[1])} # set equation + QUAD_DEG = 20 + NPOINT_INTERIOR = 12 + NPOINT_IC = 1 + def kernel_func(x, s): return np.exp(s - x) @@ -52,45 +55,33 @@ def func(out): equation = { "volterra": ppsci.equation.Volterra( - cfg.BOUNDS[0], - cfg.TRAIN.npoint_interior, - cfg.TRAIN.quad_deg, + BOUNDS[0], + NPOINT_INTERIOR, + QUAD_DEG, kernel_func, func, ) } # set constraint - # set transform for input data - def input_data_quad_transform( - input: Dict[str, np.ndarray], - weight: Dict[str, np.ndarray], - label: Dict[str, np.ndarray], - ) -> Tuple[ - Dict[str, paddle.Tensor], Dict[str, paddle.Tensor], Dict[str, paddle.Tensor] - ]: + ITERS_PER_EPOCH = 1 + # set input transform + def quad_transform(in_: Dict[str, paddle.Tensor]) -> Dict[str, paddle.Tensor]: """Get sampling points for integral. Args: - input (Dict[str, paddle.Tensor]): Raw input dict. - weight (Dict[str, paddle.Tensor]): Raw weight dict. - label (Dict[str, paddle.Tensor]): Raw label dict. + in_ (Dict[str, paddle.Tensor]): Raw input dict. Returns: - Tuple[ Dict[str, paddle.Tensor], Dict[str, paddle.Tensor], Dict[str, paddle.Tensor] ]: - Input dict contained sampling points, weight dict and label dict. + Dict[str, paddle.Tensor]: Input dict contained sampling points. """ - x = input["x"] # N points. + x = in_["x"] # N points. x_quad = equation["volterra"].get_quad_points(x).reshape([-1, 1]) # NxQ x_quad = paddle.concat((x, x_quad), axis=0) # M+MxQ: [M|Q1|Q2,...,QM|] - return ( - { - **input, - "x": x_quad, - }, - weight, - label, - ) + return { + **in_, + "x": x_quad, + } # interior constraint ide_constraint = ppsci.constraint.InteriorConstraint( @@ -103,13 +94,13 @@ def input_data_quad_transform( "transforms": ( { "FunctionalTransform": { - "transform_func": input_data_quad_transform, + "transform_func": quad_transform, }, }, ), }, - "batch_size": cfg.TRAIN.npoint_interior, - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "batch_size": NPOINT_INTERIOR, + "iters_per_epoch": ITERS_PER_EPOCH, }, ppsci.loss.MSELoss("mean"), evenly=True, @@ -128,8 +119,8 @@ def u_solution_func(in_): geom["timedomain"], { "dataset": {"name": "IterableNamedArrayDataset"}, - "batch_size": cfg.TRAIN.npoint_ic, - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "batch_size": NPOINT_IC, + "iters_per_epoch": ITERS_PER_EPOCH, }, ppsci.loss.MSELoss("mean"), criteria=geom["timedomain"].on_initial, @@ -141,17 +132,28 @@ def u_solution_func(in_): ic.name: ic, } + # set training hyper-parameters + EPOCHS = 1 if not args.epochs else args.epochs + # set optimizer - optimizer = ppsci.optimizer.LBFGS(**cfg.TRAIN.optimizer)(model) + optimizer = ppsci.optimizer.LBFGS( + learning_rate=1, + max_iter=15000, + max_eval=1250, + tolerance_grad=1e-8, + tolerance_change=0, + history_size=100, + )(model) # set validator + NPOINT_EVAL = 100 l2rel_validator = ppsci.validate.GeometryValidator( {"u": lambda out: out["u"]}, {"u": u_solution_func}, geom["timedomain"], { "dataset": "IterableNamedArrayDataset", - "total_size": cfg.EVAL.npoint_eval, + "total_size": NPOINT_EVAL, }, ppsci.loss.L2RelLoss(), evenly=True, @@ -164,18 +166,16 @@ def u_solution_func(in_): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, - epochs=cfg.TRAIN.epochs, - iters_per_epoch=cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - eval_freq=cfg.TRAIN.eval_freq, + epochs=EPOCHS, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=1, equation=equation, geom=geom, validator=validator, - pretrained_model_path=cfg.TRAIN.pretrained_model_path, - checkpoint_path=cfg.TRAIN.checkpoint_path, - eval_with_no_grad=cfg.EVAL.eval_with_no_grad, + eval_with_no_grad=True, ) # train model solver.train() @@ -191,78 +191,4 @@ def u_solution_func(in_): plt.xlabel(r"$t$") plt.ylabel(r"$u$") plt.title(r"$u-t$") - plt.savefig(osp.join(cfg.output_dir, "./Volterra_IDE.png"), dpi=200) - - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - - # set output directory - logger.init_logger("ppsci", osp.join(cfg.output_dir, "eval.log"), "info") - - # set model - model = ppsci.arch.MLP(**cfg.MODEL) - - # set geometry - geom = {"timedomain": ppsci.geometry.TimeDomain(*cfg.BOUNDS)} - # set validator - - def u_solution_func(in_) -> np.ndarray: - if isinstance(in_["x"], paddle.Tensor): - return paddle.exp(-in_["x"]) * paddle.cosh(in_["x"]) - return np.exp(-in_["x"]) * np.cosh(in_["x"]) - - l2rel_validator = ppsci.validate.GeometryValidator( - {"u": lambda out: out["u"]}, - {"u": u_solution_func}, - geom["timedomain"], - { - "dataset": "IterableNamedArrayDataset", - "total_size": cfg.EVAL.npoint_eval, - }, - ppsci.loss.L2RelLoss(), - evenly=True, - metric={"L2Rel": ppsci.metric.L2Rel()}, - name="L2Rel_Validator", - ) - validator = {l2rel_validator.name: l2rel_validator} - - # initialize solver - solver = ppsci.solver.Solver( - model, - output_dir=cfg.output_dir, - geom=geom, - validator=validator, - pretrained_model_path=cfg.EVAL.pretrained_model_path, - eval_with_no_grad=cfg.EVAL.eval_with_no_grad, - ) - # evaluate model - solver.eval() - - # visualize prediction - input_data = geom["timedomain"].uniform_points(cfg.EVAL.npoint_eval) - label_data = u_solution_func({"x": input_data}) - output_data = solver.predict({"x": input_data}, return_numpy=True)["u"] - - plt.plot(input_data, label_data, "-", label=r"$u(t)$") - plt.plot(input_data, output_data, "o", label=r"$\hat{u}(t)$", markersize=4.0) - plt.legend() - plt.xlabel(r"$t$") - plt.ylabel(r"$u$") - plt.title(r"$u-t$") - plt.savefig(osp.join(cfg.output_dir, "./Volterra_IDE.png"), dpi=200) - - -@hydra.main(version_base=None, config_path="./conf", config_name="volterra_ide.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() + plt.savefig("./Volterra_IDE.png", dpi=200) diff --git a/examples/laplace/laplace2d.py b/examples/laplace/laplace2d.py index 7e30cc4fa..fe8eacd3b 100644 --- a/examples/laplace/laplace2d.py +++ b/examples/laplace/laplace2d.py @@ -12,35 +12,34 @@ # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp - -import hydra +# This code is based on PaddleScience/ppsci API import numpy as np -from omegaconf import DictConfig import ppsci +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) + # set training hyper-parameters + EPOCHS = 20000 if not args.epochs else args.epochs + ITERS_PER_EPOCH = 1 + EVAL_FREQ = 200 - # # set output directory - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + # set output directory + OUTPUT_DIR = "./output_laplace2d" if not args.output_dir else args.output_dir + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.MLP(**cfg.MODEL) + model = ppsci.arch.MLP(("x", "y"), ("u",), 5, 20) # set equation equation = {"laplace": ppsci.equation.Laplace(dim=2)} # set geometry - geom = { - "rect": ppsci.geometry.Rectangle( - cfg.DIAGONAL_COORD.xmin, cfg.DIAGONAL_COORD.xmax - ) - } + geom = {"rect": ppsci.geometry.Rectangle((0.0, 0.0), (1.0, 1.0))} # compute ground truth function def u_solution_func(out): @@ -51,10 +50,12 @@ def u_solution_func(out): # set train dataloader config train_dataloader_cfg = { "dataset": "IterableNamedArrayDataset", - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "iters_per_epoch": ITERS_PER_EPOCH, } - NPOINT_TOTAL = cfg.NPOINT_INTERIOR + cfg.NPOINT_BC + NPOINT_INTERIOR = 99**2 + NPOINT_BC = 400 + NPOINT_TOTAL = NPOINT_INTERIOR + NPOINT_BC # set constraint pde_constraint = ppsci.constraint.InteriorConstraint( @@ -70,7 +71,7 @@ def u_solution_func(out): {"u": lambda out: out["u"]}, {"u": u_solution_func}, geom["rect"], - {**train_dataloader_cfg, "batch_size": cfg.NPOINT_BC}, + {**train_dataloader_cfg, "batch_size": NPOINT_BC}, ppsci.loss.MSELoss("sum"), name="BC", ) @@ -81,7 +82,7 @@ def u_solution_func(out): } # set optimizer - optimizer = ppsci.optimizer.Adam(learning_rate=cfg.TRAIN.learning_rate)(model) + optimizer = ppsci.optimizer.Adam(learning_rate=0.001)(model) # set validator mse_metric = ppsci.validate.GeometryValidator( @@ -103,7 +104,7 @@ def u_solution_func(out): # set visualizer(optional) vis_points = geom["rect"].sample_interior(NPOINT_TOTAL, evenly=True) visualizer = { - "visualize_u": ppsci.visualize.VisualizerVtu( + "visulzie_u": ppsci.visualize.VisualizerVtu( vis_points, {"u": lambda d: d["u"]}, num_timestamps=1, @@ -115,12 +116,12 @@ def u_solution_func(out): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, - epochs=cfg.TRAIN.epochs, - iters_per_epoch=cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - eval_freq=cfg.TRAIN.eval_freq, + epochs=EPOCHS, + iters_per_epoch=ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=EVAL_FREQ, equation=equation, geom=geom, validator=validator, @@ -133,87 +134,18 @@ def u_solution_func(out): # visualize prediction after finished training solver.visualize() - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # set output directory - logger.init_logger("ppsci", osp.join(cfg.output_dir, "eval.log"), "info") - - # set model - model = ppsci.arch.MLP(**cfg.MODEL) - - # set equation - equation = {"laplace": ppsci.equation.Laplace(dim=2)} - - # set geometry - geom = { - "rect": ppsci.geometry.Rectangle( - cfg.DIAGONAL_COORD.xmin, cfg.DIAGONAL_COORD.xmax - ) - } - - # compute ground truth function - def u_solution_func(out): - """compute ground truth for u as label data""" - x, y = out["x"], out["y"] - return np.cos(x) * np.cosh(y) - - NPOINT_TOTAL = cfg.NPOINT_INTERIOR + cfg.NPOINT_BC - - # set validator - mse_metric = ppsci.validate.GeometryValidator( - {"u": lambda out: out["u"]}, - {"u": u_solution_func}, - geom["rect"], - { - "dataset": "IterableNamedArrayDataset", - "total_size": NPOINT_TOTAL, - }, - ppsci.loss.MSELoss(), - evenly=True, - metric={"MSE": ppsci.metric.MSE()}, - with_initial=True, - name="MSE_Metric", - ) - validator = {mse_metric.name: mse_metric} - - # set visualizer(optional) - vis_points = geom["rect"].sample_interior(NPOINT_TOTAL, evenly=True) - visualizer = { - "visualize_u": ppsci.visualize.VisualizerVtu( - vis_points, - {"u": lambda d: d["u"]}, - num_timestamps=1, - prefix="result_u", - ) - } - - # initialize solver + # directly evaluate model from pretrained_model_path(optional) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") solver = ppsci.solver.Solver( model, - output_dir=cfg.output_dir, - seed=cfg.seed, + constraint, + OUTPUT_DIR, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - pretrained_model_path=cfg.EVAL.pretrained_model_path, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", ) solver.eval() - # visualize prediction after finished training + # visualize prediction from pretrained_model_path(optional) solver.visualize() - - -@hydra.main(version_base=None, config_path="./conf", config_name="laplace2d.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/ldc/ldc2d_steady_Re10.py b/examples/ldc/ldc2d_steady_Re10.py index c7eec4f3e..b3454703b 100644 --- a/examples/ldc/ldc2d_steady_Re10.py +++ b/examples/ldc/ldc2d_steady_Re10.py @@ -11,35 +11,36 @@ # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp -import hydra import numpy as np -from omegaconf import DictConfig import ppsci +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) + # set output directory + OUTPUT_DIR = "./ldc2d_steady_Re10" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.MLP(**cfg.MODEL.model) + model = ppsci.arch.MLP(("x", "y"), ("u", "v", "p"), 9, 50, "tanh") # set equation - equation = {"NavierStokes": ppsci.equation.NavierStokes(cfg.NU, cfg.RHO, 2, False)} + equation = {"NavierStokes": ppsci.equation.NavierStokes(0.01, 1.0, 2, False)} # set geometry geom = {"rect": ppsci.geometry.Rectangle((-0.05, -0.05), (0.05, 0.05))} # set dataloader config + ITERS_PER_EPOCH = 1 train_dataloader_cfg = { "dataset": "IterableNamedArrayDataset", - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "iters_per_epoch": ITERS_PER_EPOCH, } NPOINT_PDE = 99**2 @@ -49,14 +50,18 @@ def train(cfg: DictConfig): NPOINT_RIGHT = 99 # set constraint - pde = ppsci.constraint.InteriorConstraint( + pde_constraint = ppsci.constraint.InteriorConstraint( equation["NavierStokes"].equations, {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, geom["rect"], {**train_dataloader_cfg, "batch_size": NPOINT_PDE}, ppsci.loss.MSELoss("sum"), evenly=True, - weight_dict=cfg.TRAIN.weight.pde, + weight_dict={ + "continuity": 0.0001, + "momentum_x": 0.0001, + "momentum_y": 0.0001, + }, name="EQ", ) bc_top = ppsci.constraint.BoundaryConstraint( @@ -97,18 +102,23 @@ def train(cfg: DictConfig): ) # wrap constraints together constraint = { - pde.name: pde, + pde_constraint.name: pde_constraint, bc_top.name: bc_top, bc_bottom.name: bc_bottom, bc_left.name: bc_left, bc_right.name: bc_right, } - # set optimizer + # set training hyper-parameters + EPOCHS = 20000 if not args.epochs else args.epochs lr_scheduler = ppsci.optimizer.lr_scheduler.Cosine( - **cfg.TRAIN.lr_scheduler, - warmup_epoch=int(0.05 * cfg.TRAIN.epochs), + EPOCHS, + ITERS_PER_EPOCH, + 0.001, + warmup_epoch=int(0.05 * EPOCHS), )() + + # set optimizer optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) # set validator @@ -120,7 +130,7 @@ def train(cfg: DictConfig): { "dataset": "NamedArrayDataset", "total_size": NPOINT_EVAL, - "batch_size": cfg.EVAL.batch_size.residual_validator, + "batch_size": 8192, "sampler": {"name": "BatchSampler"}, }, ppsci.loss.MSELoss("sum"), @@ -135,7 +145,7 @@ def train(cfg: DictConfig): NPOINT_BC = NPOINT_TOP + NPOINT_BOTTOM + NPOINT_LEFT + NPOINT_RIGHT vis_points = geom["rect"].sample_interior(NPOINT_PDE + NPOINT_BC, evenly=True) visualizer = { - "visualize_u_v": ppsci.visualize.VisualizerVtu( + "visulzie_u_v": ppsci.visualize.VisualizerVtu( vis_points, {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, prefix="result_u_v", @@ -146,18 +156,17 @@ def train(cfg: DictConfig): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, lr_scheduler, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.EVAL.pretrained_model_path, - eval_freq=cfg.TRAIN.eval_freq, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=200, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - checkpoint_path=cfg.TRAIN.checkpoint_path, ) # train model solver.train() @@ -166,85 +175,18 @@ def train(cfg: DictConfig): # visualize prediction after finished training solver.visualize() - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "eval.log"), "info") - - # set model - model = ppsci.arch.MLP(**cfg.MODEL.model) - - # set equation - equation = {"NavierStokes": ppsci.equation.NavierStokes(cfg.NU, cfg.RHO, 2, False)} - - # set geometry - geom = {"rect": ppsci.geometry.Rectangle((-0.05, -0.05), (0.05, 0.05))} - - NPOINT_PDE = 99**2 - NPOINT_TOP = 101 - NPOINT_BOTTOM = 101 - NPOINT_LEFT = 99 - NPOINT_RIGHT = 99 - - # set validator - NPOINT_EVAL = NPOINT_PDE - residual_validator = ppsci.validate.GeometryValidator( - equation["NavierStokes"].equations, - {"momentum_x": 0, "continuity": 0, "momentum_y": 0}, - geom["rect"], - { - "dataset": "NamedArrayDataset", - "total_size": NPOINT_EVAL, - "batch_size": cfg.EVAL.batch_size.residual_validator, - "sampler": {"name": "BatchSampler"}, - }, - ppsci.loss.MSELoss("sum"), - evenly=True, - metric={"MSE": ppsci.metric.MSE()}, - name="Residual", - ) - validator = {residual_validator.name: residual_validator} - - # set visualizer(optional) - # manually collate input data for visualization, - NPOINT_BC = NPOINT_TOP + NPOINT_BOTTOM + NPOINT_LEFT + NPOINT_RIGHT - vis_points = geom["rect"].sample_interior(NPOINT_PDE + NPOINT_BC, evenly=True) - visualizer = { - "visualize_u_v": ppsci.visualize.VisualizerVtu( - vis_points, - {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, - prefix="result_u_v", - ) - } - - # initialize solver + # directly evaluate pretrained model(optional) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") solver = ppsci.solver.Solver( model, - output_dir=cfg.output_dir, + constraint, + OUTPUT_DIR, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - pretrained_model_path=cfg.EVAL.pretrained_model_path, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", ) solver.eval() # visualize prediction for pretrained model(optional) solver.visualize() - - -@hydra.main( - version_base=None, config_path="./conf", config_name="ldc2d_steady_Re10.yaml" -) -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/ldc/ldc2d_unsteady_Re10.py b/examples/ldc/ldc2d_unsteady_Re10.py index 6d093e057..ac22f23de 100644 --- a/examples/ldc/ldc2d_unsteady_Re10.py +++ b/examples/ldc/ldc2d_unsteady_Re10.py @@ -11,30 +11,30 @@ # WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. # See the License for the specific language governing permissions and # limitations under the License. -from os import path as osp -import hydra import numpy as np -from omegaconf import DictConfig import ppsci +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + ppsci.utils.misc.set_random_seed(42) + # set output directory + OUTPUT_DIR = "./ldc2d_unsteady_Re10" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.MLP(**cfg.MODEL.model) + model = ppsci.arch.MLP(("t", "x", "y"), ("u", "v", "p"), 9, 50, "tanh") # set equation - equation = {"NavierStokes": ppsci.equation.NavierStokes(cfg.NU, cfg.RHO, 2, True)} + equation = {"NavierStokes": ppsci.equation.NavierStokes(0.01, 1.0, 2, True)} # set timestamps(including initial t0) - timestamps = np.linspace(0.0, 1.5, cfg.NTIME_ALL, endpoint=True) + timestamps = np.linspace(0.0, 1.5, 16, endpoint=True) # set time-geometry geom = { "time_rect": ppsci.geometry.TimeXGeometry( @@ -44,28 +44,34 @@ def train(cfg: DictConfig): } # set dataloader config + ITERS_PER_EPOCH = 1 train_dataloader_cfg = { "dataset": "IterableNamedArrayDataset", - "iters_per_epoch": cfg.TRAIN.iters_per_epoch, + "iters_per_epoch": ITERS_PER_EPOCH, } # pde/bc constraint use t1~tn, initial constraint use t0 - NPOINT_PDE, NTIME_PDE = 99**2, cfg.NTIME_ALL - 1 - NPOINT_TOP, NTIME_TOP = 101, cfg.NTIME_ALL - 1 - NPOINT_DOWN, NTIME_DOWN = 101, cfg.NTIME_ALL - 1 - NPOINT_LEFT, NTIME_LEFT = 99, cfg.NTIME_ALL - 1 - NPOINT_RIGHT, NTIME_RIGHT = 99, cfg.NTIME_ALL - 1 + NTIME_ALL = len(timestamps) + NPOINT_PDE, NTIME_PDE = 99**2, NTIME_ALL - 1 + NPOINT_TOP, NTIME_TOP = 101, NTIME_ALL - 1 + NPOINT_DOWN, NTIME_DOWN = 101, NTIME_ALL - 1 + NPOINT_LEFT, NTIME_LEFT = 99, NTIME_ALL - 1 + NPOINT_RIGHT, NTIME_RIGHT = 99, NTIME_ALL - 1 NPOINT_IC, NTIME_IC = 99**2, 1 # set constraint - pde = ppsci.constraint.InteriorConstraint( + pde_constraint = ppsci.constraint.InteriorConstraint( equation["NavierStokes"].equations, {"continuity": 0, "momentum_x": 0, "momentum_y": 0}, geom["time_rect"], {**train_dataloader_cfg, "batch_size": NPOINT_PDE * NTIME_PDE}, ppsci.loss.MSELoss("sum"), evenly=True, - weight_dict=cfg.TRAIN.weight.pde, # (1) + weight_dict={ + "continuity": 0.0001, + "momentum_x": 0.0001, + "momentum_y": 0.0001, + }, name="EQ", ) bc_top = ppsci.constraint.BoundaryConstraint( @@ -115,7 +121,7 @@ def train(cfg: DictConfig): ) # wrap constraints together constraint = { - pde.name: pde, + pde_constraint.name: pde_constraint, bc_top.name: bc_top, bc_down.name: bc_down, bc_left.name: bc_left, @@ -124,16 +130,19 @@ def train(cfg: DictConfig): } # set training hyper-parameters + EPOCHS = 20000 if not args.epochs else args.epochs lr_scheduler = ppsci.optimizer.lr_scheduler.Cosine( - **cfg.TRAIN.lr_scheduler, - warmup_epoch=int(0.05 * cfg.TRAIN.epochs), + EPOCHS, + ITERS_PER_EPOCH, + 0.001, + warmup_epoch=int(0.05 * EPOCHS), )() # set optimizer optimizer = ppsci.optimizer.Adam(lr_scheduler)(model) # set validator - NPOINT_EVAL = NPOINT_PDE * cfg.NTIME_ALL + NPOINT_EVAL = NPOINT_PDE * NTIME_ALL residual_validator = ppsci.validate.GeometryValidator( equation["NavierStokes"].equations, {"momentum_x": 0, "continuity": 0, "momentum_y": 0}, @@ -141,7 +150,7 @@ def train(cfg: DictConfig): { "dataset": "NamedArrayDataset", "total_size": NPOINT_EVAL, - "batch_size": cfg.EVAL.batch_size.residual_validator, + "batch_size": 8192, "sampler": {"name": "BatchSampler"}, }, ppsci.loss.MSELoss("sum"), @@ -177,10 +186,10 @@ def train(cfg: DictConfig): ) visualizer = { - "visualize_u_v": ppsci.visualize.VisualizerVtu( + "visulzie_u_v": ppsci.visualize.VisualizerVtu( vis_points, {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, - num_timestamps=cfg.NTIME_ALL, + num_timestamps=NTIME_ALL, prefix="result_u_v", ) } @@ -189,13 +198,13 @@ def train(cfg: DictConfig): solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, lr_scheduler, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.EVAL.pretrained_model_path, - eval_freq=cfg.TRAIN.eval_freq, + EPOCHS, + ITERS_PER_EPOCH, + eval_during_train=True, + eval_freq=200, equation=equation, geom=geom, validator=validator, @@ -208,117 +217,17 @@ def train(cfg: DictConfig): # visualize prediction after finished training solver.visualize() - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "eval.log"), "info") - - # set model - model = ppsci.arch.MLP(**cfg.MODEL.model) - - # set equation - equation = {"NavierStokes": ppsci.equation.NavierStokes(cfg.NU, cfg.RHO, 2, True)} - - # set timestamps(including initial t0) - timestamps = np.linspace(0.0, 1.5, cfg.NTIME_ALL, endpoint=True) - # set time-geometry - geom = { - "time_rect": ppsci.geometry.TimeXGeometry( - ppsci.geometry.TimeDomain(0.0, 1.5, timestamps=timestamps), - ppsci.geometry.Rectangle((-0.05, -0.05), (0.05, 0.05)), - ) - } - - # pde/bc constraint use t1~tn, initial constraint use t0 - NPOINT_PDE = 99**2 - NPOINT_TOP = 101 - NPOINT_DOWN = 101 - NPOINT_LEFT = 99 - NPOINT_RIGHT = 99 - NPOINT_IC = 99**2 - NTIME_PDE = cfg.NTIME_ALL - 1 - - # set validator - NPOINT_EVAL = NPOINT_PDE * cfg.NTIME_ALL - residual_validator = ppsci.validate.GeometryValidator( - equation["NavierStokes"].equations, - {"momentum_x": 0, "continuity": 0, "momentum_y": 0}, - geom["time_rect"], - { - "dataset": "NamedArrayDataset", - "total_size": NPOINT_EVAL, - "batch_size": cfg.EVAL.batch_size.residual_validator, - "sampler": {"name": "BatchSampler"}, - }, - ppsci.loss.MSELoss("sum"), - evenly=True, - metric={"MSE": ppsci.metric.MSE()}, - with_initial=True, - name="Residual", - ) - validator = {residual_validator.name: residual_validator} - - # set visualizer(optional) - NPOINT_BC = NPOINT_TOP + NPOINT_DOWN + NPOINT_LEFT + NPOINT_RIGHT - vis_initial_points = geom["time_rect"].sample_initial_interior( - (NPOINT_IC + NPOINT_BC), evenly=True - ) - vis_pde_points = geom["time_rect"].sample_interior( - (NPOINT_PDE + NPOINT_BC) * NTIME_PDE, evenly=True - ) - vis_points = vis_initial_points - # manually collate input data for visualization, - # (interior+boundary) x all timestamps - for t in range(NTIME_PDE): - for key in geom["time_rect"].dim_keys: - vis_points[key] = np.concatenate( - ( - vis_points[key], - vis_pde_points[key][ - t - * (NPOINT_PDE + NPOINT_BC) : (t + 1) - * (NPOINT_PDE + NPOINT_BC) - ], - ) - ) - - visualizer = { - "visualize_u_v": ppsci.visualize.VisualizerVtu( - vis_points, - {"u": lambda d: d["u"], "v": lambda d: d["v"], "p": lambda d: d["p"]}, - num_timestamps=cfg.NTIME_ALL, - prefix="result_u_v", - ) - } - # directly evaluate pretrained model(optional) solver = ppsci.solver.Solver( model, - output_dir=cfg.output_dir, + constraint, + OUTPUT_DIR, equation=equation, geom=geom, validator=validator, visualizer=visualizer, - pretrained_model_path=cfg.EVAL.pretrained_model_path, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", ) solver.eval() # visualize prediction for pretrained model(optional) solver.visualize() - - -@hydra.main( - version_base=None, config_path="./conf", config_name="ldc2d_unsteady_Re10.yaml" -) -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/lorenz/train_transformer.py b/examples/lorenz/train_transformer.py index 0c54b1b69..5b3b375f5 100644 --- a/examples/lorenz/train_transformer.py +++ b/examples/lorenz/train_transformer.py @@ -170,14 +170,14 @@ def __call__(self, x: Dict[str, paddle.Tensor]): # set visualizer(optional) states = mse_validator.data_loader.dataset.data embedding_data = mse_validator.data_loader.dataset.embedding_data - vis_data = { + vis_datas = { "embeds": embedding_data[:VIS_DATA_NUMS, :-1, :], "states": states[:VIS_DATA_NUMS, 1:, :], } visualizer = { - "visualize_states": ppsci.visualize.VisualizerScatter3D( - vis_data, + "visulzie_states": ppsci.visualize.VisualizerScatter3D( + vis_datas, { "pred_states": lambda d: output_transform(d), "states": lambda d: d["states"], diff --git a/examples/operator_learning/deeponet.py b/examples/operator_learning/deeponet.py index 75ae18edd..41c93e567 100644 --- a/examples/operator_learning/deeponet.py +++ b/examples/operator_learning/deeponet.py @@ -3,34 +3,51 @@ """ import os -from os import path as osp from typing import Callable from typing import Tuple -import hydra import numpy as np import paddle from matplotlib import pyplot as plt -from omegaconf import DictConfig import ppsci +from ppsci.utils import config from ppsci.utils import logger - -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) + SEED = 2023 + ppsci.utils.misc.set_random_seed(SEED) + # set output directory + OUTPUT_DIR = "./output_DeepONet" if not args.output_dir else args.output_dir # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") # set model - model = ppsci.arch.DeepONet(**cfg.MODEL) + NUM_SENSORS = 100 + NUM_FEATURES = 40 + model = ppsci.arch.DeepONet( + "u", + "y", + "G", + NUM_SENSORS, + NUM_FEATURES, + 1, + 1, + 40, + 40, + branch_activation="relu", + trunk_activation="relu", + use_bias=True, + ) # set dataloader config + ITERS_PER_EPOCH = 1 train_dataloader_cfg = { "dataset": { "name": "IterableNPZDataset", - "file_path": cfg.TRAIN_FILE_PATH, + "file_path": "./antiderivative_unaligned_train.npz", "input_keys": ("u", "y"), "label_keys": ("G",), "alias_dict": {"u": "X_train0", "y": "X_train1", "G": "y_train"}, @@ -45,14 +62,17 @@ def train(cfg: DictConfig): # wrap constraints together constraint = {sup_constraint.name: sup_constraint} + # set training hyper-parameters + EPOCHS = 10000 if not args.epochs else args.epochs + # set optimizer - optimizer = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model) + optimizer = ppsci.optimizer.Adam(1e-3)(model) # set validator eval_dataloader_cfg = { "dataset": { "name": "IterableNPZDataset", - "file_path": cfg.VALID_FILE_PATH, + "file_path": "./antiderivative_unaligned_test.npz", "input_keys": ("u", "y"), "label_keys": ("G",), "alias_dict": {"u": "X_test0", "y": "X_test1", "G": "y_test"}, @@ -68,128 +88,42 @@ def train(cfg: DictConfig): validator = {sup_validator.name: sup_validator} # initialize solver + EVAL_FREQ = 500 solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, None, - cfg.TRAIN.epochs, - cfg.TRAIN.iters_per_epoch, - save_freq=cfg.TRAIN.save_freq, - eval_freq=cfg.TRAIN.eval_freq, - log_freq=cfg.log_freq, - seed=cfg.seed, + EPOCHS, + ITERS_PER_EPOCH, + save_freq=EVAL_FREQ, + log_freq=20, + eval_during_train=True, + eval_freq=EVAL_FREQ, + seed=SEED, validator=validator, - eval_during_train=cfg.TRAIN.eval_during_train, - checkpoint_path=cfg.TRAIN.checkpoint_path, + eval_with_no_grad=True, ) # train model solver.train() # evaluate after finished training solver.eval() - # visualize prediction for different functions u and corresponding G(u) - dtype = paddle.get_default_dtype() - - def generate_y_u_G_ref( - u_func: Callable, G_u_func: Callable - ) -> Tuple[np.ndarray, np.ndarray, np.ndarray]: - """Generate discretized data of given function u and corresponding G(u). - - Args: - u_func (Callable): Function u. - G_u_func (Callable): Function G(u). - - Returns: - Tuple[np.ndarray, np.ndarray, np.ndarray]: Discretized data of u, y and G(u). - """ - x = np.linspace(0, 1, cfg.MODEL.num_loc, dtype=dtype).reshape( - [1, cfg.MODEL.num_loc] - ) - u = u_func(x) - u = np.tile(u, [cfg.NUM_Y, 1]) - - y = np.linspace(0, 1, cfg.NUM_Y, dtype=dtype).reshape([cfg.NUM_Y, 1]) - G_ref = G_u_func(y) - return u, y, G_ref - - func_u_G_pair = [ - # (title_string, func_u, func_G(u)), s.t. dG/dx == u and G(u)(0) = 0 - (r"$u=\cos(x), G(u)=sin(x$)", lambda x: np.cos(x), lambda y: np.sin(y)), # 1 - ( - r"$u=sec^2(x), G(u)=tan(x$)", - lambda x: (1 / np.cos(x)) ** 2, - lambda y: np.tan(y), - ), # 2 - ( - r"$u=sec(x)tan(x), G(u)=sec(x) - 1$", - lambda x: (1 / np.cos(x) * np.tan(x)), - lambda y: 1 / np.cos(y) - 1, - ), # 3 - ( - r"$u=1.5^x\ln{1.5}, G(u)=1.5^x-1$", - lambda x: 1.5**x * np.log(1.5), - lambda y: 1.5**y - 1, - ), # 4 - (r"$u=3x^2, G(u)=x^3$", lambda x: 3 * x**2, lambda y: y**3), # 5 - (r"$u=4x^3, G(u)=x^4$", lambda x: 4 * x**3, lambda y: y**4), # 6 - (r"$u=5x^4, G(u)=x^5$", lambda x: 5 * x**4, lambda y: y**5), # 7 - (r"$u=6x^5, G(u)=x^6$", lambda x: 5 * x**4, lambda y: y**5), # 8 - (r"$u=e^x, G(u)=e^x-1$", lambda x: np.exp(x), lambda y: np.exp(y) - 1), # 9 - ] - - os.makedirs(os.path.join(cfg.output_dir, "visual"), exist_ok=True) - for i, (title, u_func, G_func) in enumerate(func_u_G_pair): - u, y, G_ref = generate_y_u_G_ref(u_func, G_func) - G_pred = solver.predict({"u": u, "y": y}, return_numpy=True)["G"] - plt.plot(y, G_pred, label=r"$G(u)(y)_{ref}$") - plt.plot(y, G_ref, label=r"$G(u)(y)_{pred}$") - plt.legend() - plt.title(title) - plt.savefig(os.path.join(cfg.output_dir, "visual", f"func_{i}_result.png")) - plt.clf() - - -def evaluate(cfg: DictConfig): - # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") - - # set model - model = ppsci.arch.DeepONet(**cfg.MODEL) - - # set validator - eval_dataloader_cfg = { - "dataset": { - "name": "IterableNPZDataset", - "file_path": cfg.VALID_FILE_PATH, - "input_keys": ("u", "y"), - "label_keys": ("G",), - "alias_dict": {"u": "X_test0", "y": "X_test1", "G": "y_test"}, - }, - } - sup_validator = ppsci.validate.SupervisedValidator( - eval_dataloader_cfg, - ppsci.loss.MSELoss(), - {"G": lambda out: out["G"]}, - metric={"MeanL2Rel": ppsci.metric.MeanL2Rel()}, - name="G_eval", - ) - validator = {sup_validator.name: sup_validator} - + # directly evaluate pretrained model(optional) + logger.init_logger("ppsci", f"{OUTPUT_DIR}/eval.log", "info") solver = ppsci.solver.Solver( model, None, - cfg.output_dir, + OUTPUT_DIR, validator=validator, - pretrained_model_path=cfg.EVAL.pretrained_model_path, - eval_with_no_grad=cfg.EVAL.eval_with_no_grad, + pretrained_model_path=f"{OUTPUT_DIR}/checkpoints/latest", + eval_with_no_grad=True, ) solver.eval() # visualize prediction for different functions u and corresponding G(u) + NUM_Y = 1000 # number of y point for G(u) to be visualized dtype = paddle.get_default_dtype() def generate_y_u_G_ref( @@ -204,13 +138,11 @@ def generate_y_u_G_ref( Returns: Tuple[np.ndarray, np.ndarray, np.ndarray]: Discretized data of u, y and G(u). """ - x = np.linspace(0, 1, cfg.MODEL.num_loc, dtype=dtype).reshape( - [1, cfg.MODEL.num_loc] - ) + x = np.linspace(0, 1, NUM_SENSORS, dtype=dtype).reshape([1, NUM_SENSORS]) u = u_func(x) - u = np.tile(u, [cfg.NUM_Y, 1]) + u = np.tile(u, [NUM_Y, 1]) - y = np.linspace(0, 1, cfg.NUM_Y, dtype=dtype).reshape([cfg.NUM_Y, 1]) + y = np.linspace(0, 1, NUM_Y, dtype=dtype).reshape([NUM_Y, 1]) G_ref = G_u_func(y) return u, y, G_ref @@ -239,7 +171,7 @@ def generate_y_u_G_ref( (r"$u=e^x, G(u)=e^x-1$", lambda x: np.exp(x), lambda y: np.exp(y) - 1), # 9 ] - os.makedirs(os.path.join(cfg.output_dir, "visual"), exist_ok=True) + os.makedirs(os.path.join(OUTPUT_DIR, "visual"), exist_ok=True) for i, (title, u_func, G_func) in enumerate(func_u_G_pair): u, y, G_ref = generate_y_u_G_ref(u_func, G_func) G_pred = solver.predict({"u": u, "y": y}, return_numpy=True)["G"] @@ -247,19 +179,5 @@ def generate_y_u_G_ref( plt.plot(y, G_ref, label=r"$G(u)(y)_{pred}$") plt.legend() plt.title(title) - plt.savefig(os.path.join(cfg.output_dir, "visual", f"func_{i}_result.png")) + plt.savefig(os.path.join(OUTPUT_DIR, "visual", f"func_{i}_result.png")) plt.clf() - - -@hydra.main(version_base=None, config_path="./conf", config_name="deeponet.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/examples/pipe/poiseuille_flow.py b/examples/pipe/poiseuille_flow.py index c40de3ee6..8b270bf54 100644 --- a/examples/pipe/poiseuille_flow.py +++ b/examples/pipe/poiseuille_flow.py @@ -18,45 +18,62 @@ import copy import os -from os import path as osp +import os.path as osp -import hydra import matplotlib.pyplot as plt import numpy as np import paddle -from omegaconf import DictConfig -import ppsci from ppsci.utils import checker -from ppsci.utils import logger if not checker.dynamic_import_to_globals("seaborn"): raise ModuleNotFoundError("Please install seaborn through pip first.") import seaborn as sns +import ppsci +from ppsci.utils import config +from ppsci.utils import logger -def train(cfg: DictConfig): +if __name__ == "__main__": + args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(cfg.seed) - # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, f"{cfg.mode}.log"), "info") + ppsci.utils.misc.set_random_seed(42) + + # set output directory + OUTPUT_DIR = "./output_poiseuille_flow" - X_OUT = cfg.X_IN + cfg.L - Y_START = -cfg.R - Y_END = Y_START + 2 * cfg.R - NU_START = cfg.NU_MEAN - cfg.NU_MEAN * cfg.NU_STD # 0.0001 - NU_END = cfg.NU_MEAN + cfg.NU_MEAN * cfg.NU_STD # 0.1 + # initialize logger + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") + + NU_MEAN = 0.001 + NU_STD = 0.9 + L = 1.0 # length of pipe + R = 0.05 # radius of pipe + RHO = 1 # density + P_OUT = 0 # pressure at the outlet of pipe + P_IN = 0.1 # pressure at the inlet of pipe + + N_x = 10 + N_y = 50 + N_p = 50 + + X_IN = 0 + X_OUT = X_IN + L + Y_START = -R + Y_END = Y_START + 2 * R + NU_START = NU_MEAN - NU_MEAN * NU_STD # 0.0001 + NU_END = NU_MEAN + NU_MEAN * NU_STD # 0.1 ## prepare data with (?, 2) data_1d_x = np.linspace( - cfg.X_IN, X_OUT, cfg.N_x, endpoint=True, dtype=paddle.get_default_dtype() + X_IN, X_OUT, N_x, endpoint=True, dtype=paddle.get_default_dtype() ) data_1d_y = np.linspace( - Y_START, Y_END, cfg.N_y, endpoint=True, dtype=paddle.get_default_dtype() + Y_START, Y_END, N_y, endpoint=True, dtype=paddle.get_default_dtype() ) data_1d_nu = np.linspace( - NU_START, NU_END, cfg.N_p, endpoint=True, dtype=paddle.get_default_dtype() + NU_START, NU_END, N_p, endpoint=True, dtype=paddle.get_default_dtype() ) data_2d_xy = ( @@ -69,36 +86,37 @@ def train(cfg: DictConfig): input_y = data_2d_xy_shuffle[:, 1].reshape(data_2d_xy_shuffle.shape[0], 1) input_nu = data_2d_xy_shuffle[:, 2].reshape(data_2d_xy_shuffle.shape[0], 1) + interior_data = {"x": input_x, "y": input_y, "nu": input_nu} interior_geom = ppsci.geometry.PointCloud( interior={"x": input_x, "y": input_y, "nu": input_nu}, coord_keys=("x", "y", "nu"), ) # set model - model_u = ppsci.arch.MLP(**cfg.MODEL.u_net) - model_v = ppsci.arch.MLP(**cfg.MODEL.v_net) - model_p = ppsci.arch.MLP(**cfg.MODEL.p_net) + model_u = ppsci.arch.MLP(("sin(x)", "cos(x)", "y", "nu"), ("u",), 3, 50, "swish") + model_v = ppsci.arch.MLP(("sin(x)", "cos(x)", "y", "nu"), ("v",), 3, 50, "swish") + model_p = ppsci.arch.MLP(("sin(x)", "cos(x)", "y", "nu"), ("p",), 3, 50, "swish") def input_trans(input): x, y = input["x"], input["y"] nu = input["nu"] - b = 2 * np.pi / (X_OUT - cfg.X_IN) - c = np.pi * (cfg.X_IN + X_OUT) / (cfg.X_IN - X_OUT) - sin_x = cfg.X_IN * paddle.sin(b * x + c) - cos_x = cfg.X_IN * paddle.cos(b * x + c) + b = 2 * np.pi / (X_OUT - X_IN) + c = np.pi * (X_IN + X_OUT) / (X_IN - X_OUT) + sin_x = X_IN * paddle.sin(b * x + c) + cos_x = X_IN * paddle.cos(b * x + c) return {"sin(x)": sin_x, "cos(x)": cos_x, "x": x, "y": y, "nu": nu} def output_trans_u(input, out): - return {"u": out["u"] * (cfg.R**2 - input["y"] ** 2)} + return {"u": out["u"] * (R**2 - input["y"] ** 2)} def output_trans_v(input, out): - return {"v": (cfg.R**2 - input["y"] ** 2) * out["v"]} + return {"v": (R**2 - input["y"] ** 2) * out["v"]} def output_trans_p(input, out): return { "p": ( - (cfg.P_IN - cfg.P_OUT) * (X_OUT - input["x"]) / cfg.L - + (cfg.X_IN - input["x"]) * (X_OUT - input["x"]) * out["p"] + (P_IN - P_OUT) * (X_OUT - input["x"]) / L + + (X_IN - input["x"]) * (X_OUT - input["x"]) * out["p"] ) } @@ -111,19 +129,16 @@ def output_trans_p(input, out): model = ppsci.arch.ModelList((model_u, model_v, model_p)) # set optimizer - optimizer = ppsci.optimizer.Adam(cfg.TRAIN.learning_rate)(model) + optimizer = ppsci.optimizer.Adam(5e-3)(model) # set euqation equation = { - "NavierStokes": ppsci.equation.NavierStokes( - nu="nu", rho=cfg.RHO, dim=2, time=False - ) + "NavierStokes": ppsci.equation.NavierStokes(nu="nu", rho=RHO, dim=2, time=False) } # set constraint - ITERS_PER_EPOCH = int( - (cfg.N_x * cfg.N_y * cfg.N_p) / cfg.TRAIN.batch_size.pde_constraint - ) + BATCH_SIZE = 128 + ITERS_PER_EPOCH = int((N_x * N_y * N_p) / BATCH_SIZE) pde_constraint = ppsci.constraint.InteriorConstraint( equation["NavierStokes"].equations, @@ -132,7 +147,7 @@ def output_trans_p(input, out): dataloader_cfg={ "dataset": "NamedArrayDataset", "num_workers": 1, - "batch_size": cfg.TRAIN.batch_size.pde_constraint, + "batch_size": BATCH_SIZE, "iters_per_epoch": ITERS_PER_EPOCH, "sampler": { "name": "BatchSampler", @@ -148,16 +163,18 @@ def output_trans_p(input, out): # wrap constraints together constraint = {pde_constraint.name: pde_constraint} + EPOCHS = 3000 if not args.epochs else args.epochs + # initialize solver solver = ppsci.solver.Solver( model, constraint, - cfg.output_dir, + OUTPUT_DIR, optimizer, - epochs=cfg.TRAIN.epochs, + epochs=EPOCHS, iters_per_epoch=ITERS_PER_EPOCH, - eval_during_train=cfg.TRAIN.eval_during_train, - save_freq=cfg.TRAIN.save_freq, + eval_during_train=False, + save_freq=10, equation=equation, ) @@ -171,23 +188,25 @@ def output_trans_p(input, out): "nu": data_2d_xy[:, 2:3], } output_dict = solver.predict(input_dict, return_numpy=True) - u_pred = output_dict["u"].reshape(cfg.N_y, cfg.N_x, cfg.N_p) + u_pred = output_dict["u"].reshape(N_y, N_x, N_p) + v_pred = output_dict["v"].reshape(N_y, N_x, N_p) + p_pred = output_dict["p"].reshape(N_y, N_x, N_p) # Analytical result, y = data_1d_y - u_analytical = np.zeros([cfg.N_y, cfg.N_x, cfg.N_p]) - dP = cfg.P_IN - cfg.P_OUT + u_analytical = np.zeros([N_y, N_x, N_p]) + dP = P_IN - P_OUT - for i in range(cfg.N_p): - uy = (cfg.R**2 - data_1d_y**2) * dP / (2 * cfg.L * data_1d_nu[i] * cfg.RHO) - u_analytical[:, :, i] = np.tile(uy.reshape([cfg.N_y, 1]), cfg.N_x) + for i in range(N_p): + uy = (R**2 - data_1d_y**2) * dP / (2 * L * data_1d_nu[i] * RHO) + u_analytical[:, :, i] = np.tile(uy.reshape([N_y, 1]), N_x) fontsize = 16 - idx_X = int(round(cfg.N_x / 2)) # pipe velocity section at L/2 + idx_X = int(round(N_x / 2)) # pipe velocity section at L/2 nu_index = [3, 6, 14, 49] # pick 4 nu samples ytext = [0.45, 0.28, 0.1, 0.01] # Plot - PLOT_DIR = osp.join(cfg.output_dir, "visu") + PLOT_DIR = osp.join(OUTPUT_DIR, "visu") os.makedirs(PLOT_DIR, exist_ok=True) plt.figure(1) plt.clf() @@ -228,9 +247,9 @@ def output_trans_p(input, out): # Distribution of center velocity # Predicted result num_test = 500 - data_1d_nu_distribution = np.random.normal(cfg.NU_MEAN, 0.2 * cfg.NU_MEAN, num_test) + data_1d_nu_distribution = np.random.normal(NU_MEAN, 0.2 * NU_MEAN, num_test) data_2d_xy_test = ( - np.array(np.meshgrid((cfg.X_IN - X_OUT) / 2.0, 0, data_1d_nu_distribution)) + np.array(np.meshgrid((X_IN - X_OUT) / 2.0, 0, data_1d_nu_distribution)) .reshape(3, -1) .T ) @@ -244,7 +263,7 @@ def output_trans_p(input, out): u_max_pred = output_dict_test["u"] # Analytical result, y = 0 - u_max_a = (cfg.R**2) * dP / (2 * cfg.L * data_1d_nu_distribution * cfg.RHO) + u_max_a = (R**2) * dP / (2 * L * data_1d_nu_distribution * RHO) # Plot plt.figure(2) @@ -271,22 +290,4 @@ def output_trans_p(input, out): plt.ylabel(r"PDF", fontsize=fontsize) ax1.tick_params(axis="x", labelsize=fontsize) ax1.tick_params(axis="y", labelsize=fontsize) - plt.savefig(osp.join(PLOT_DIR, "pipe_uniformUQ.png"), bbox_inches="tight") - - -def evaluate(cfg: DictConfig): - print("Not supported.") - - -@hydra.main(version_base=None, config_path="./conf", config_name="poiseuille_flow.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() + plt.savefig(osp.join(PLOT_DIR, "pipe_unformUQ.png"), bbox_inches="tight") diff --git a/examples/rossler/train_enn.py b/examples/rossler/train_enn.py index 6383e1b46..6d2fb7f83 100644 --- a/examples/rossler/train_enn.py +++ b/examples/rossler/train_enn.py @@ -43,7 +43,7 @@ def get_mean_std(data: np.ndarray): if __name__ == "__main__": args = config.parse_args() # set random seed for reproducibility - ppsci.utils.misc.set_random_seed(6) + ppsci.utils.misc.set_random_seed(42) # set training hyper-parameters EPOCHS = 300 if not args.epochs else args.epochs TRAIN_BLOCK_SIZE = 16 diff --git a/examples/rossler/train_transformer.py b/examples/rossler/train_transformer.py index 58bff9290..2450fccf4 100644 --- a/examples/rossler/train_transformer.py +++ b/examples/rossler/train_transformer.py @@ -167,14 +167,14 @@ def __call__(self, x: Dict[str, paddle.Tensor]): # set visualizer(optional) states = mse_validator.data_loader.dataset.data embedding_data = mse_validator.data_loader.dataset.embedding_data - vis_data = { + vis_datas = { "embeds": embedding_data[:VIS_DATA_NUMS, :-1, :], "states": states[:VIS_DATA_NUMS, 1:, :], } visualizer = { - "visualize_states": ppsci.visualize.VisualizerScatter3D( - vis_data, + "visulzie_states": ppsci.visualize.VisualizerScatter3D( + vis_datas, { "pred_states": lambda d: output_transform(d), "states": lambda d: d["states"], diff --git a/examples/shock_wave/lhs.py b/examples/shock_wave/lhs.py index 9efcbbd1b..bdc3b5940 100644 --- a/examples/shock_wave/lhs.py +++ b/examples/shock_wave/lhs.py @@ -26,7 +26,7 @@ def _partition(n_sample: int, bounds: np.ndarray) -> np.ndarray: bounds (np.ndarray): Lower and upper bound of each variable with shape [m, 2]. Returns: - np.ndarray: Partition range array with shape [m, n, 2]. + np.ndarray: Partion range array wieh shape [m, n, 2]. """ tmp = np.arange(n_sample, dtype=dtype) # [0,1,...,n-1]. coefficient_lower = np.stack([1 - tmp / n_sample, tmp / n_sample], axis=1,).astype( @@ -46,13 +46,13 @@ def _partition(n_sample: int, bounds: np.ndarray) -> np.ndarray: def _representative(partition_range: np.ndarray) -> np.ndarray: - """Compute single representative factor. + """Compute single representitive factor. Args: - partition_range (np.ndarray): Partition range array with shape [m, n, 2]. + partition_range (np.ndarray): Partion range array wieh shape [m, n, 2]. Returns: - np.ndarray: Matrix of random representative factor with shape [n, m]. + np.ndarray: Matrix of random representitive factor with shape [n, m]. """ nvar = partition_range.shape[0] nsample = partition_range.shape[1] diff --git a/examples/tempoGAN/functions.py b/examples/tempoGAN/functions.py index 68b610b1a..bcf27a384 100644 --- a/examples/tempoGAN/functions.py +++ b/examples/tempoGAN/functions.py @@ -102,7 +102,7 @@ def split_data(data: np.ndarray, tile_ratio: int) -> np.ndarray: """Split a numpy image to tiles equally. Args: - data (np.ndarray): The image to be Split. + data (np.ndarray): The image to be splited. tile_ratio (int): How many tiles of one dim. Number of result tiles is tile_ratio * tile_ratio for a 2d image. @@ -274,8 +274,8 @@ def transform_in(self, _in): return {"input_gen": density_low_inp} def loss_func_gen(self, output_dict: Dict, *args) -> paddle.Tensor: - """Calculate loss of generator when use spatial discriminator. - The loss consists of l1 loss, l2 loss and layer loss when use spatial discriminator. + """Calculate loss of generator when use spatial discraminitor. + The loss consists of l1 loss, l2 loss and layer loss when use spatial discraminitor. Notice that all item of loss is optional because weight of them might be 0. Args: @@ -326,8 +326,8 @@ def loss_func_gen(self, output_dict: Dict, *args) -> paddle.Tensor: return losses def loss_func_gen_tempo(self, output_dict: Dict, *args) -> paddle.Tensor: - """Calculate loss of generator when use temporal discriminator. - The loss is cross entropy loss when use temporal discriminator. + """Calculate loss of generator when use temporal discraminitor. + The loss is cross entropy loss when use temporal discraminitor. Args: output_dict (Dict): output dict of model. @@ -443,16 +443,9 @@ def __init__( self.density_min = density_min self.max_turn = max_turn - def transform( - self, - input_item: Dict[str, np.ndarray], - label_item: Dict[str, np.ndarray], - weight_item: Dict[str, np.ndarray], - ) -> Union[ - Dict[str, paddle.Tensor], Dict[str, paddle.Tensor], Dict[str, paddle.Tensor] - ]: + def transform(self, input_item: Dict[str, np.ndarray]) -> Dict[str, paddle.Tensor]: if self.tile_ratio == 1: - return input_item, label_item, weight_item + return input_item for _ in range(self.max_turn): rand_ratio = np.random.rand() density_low = self.cut_data(input_item["density_low"], rand_ratio) @@ -462,7 +455,7 @@ def transform( input_item["density_low"] = density_low input_item["density_high"] = density_high - return input_item, label_item, weight_item + return input_item def cut_data(self, data: np.ndarray, rand_ratio: float) -> paddle.Tensor: # data: C,H,W diff --git a/examples/tempoGAN/tempoGAN.py b/examples/tempoGAN/tempoGAN.py index 5e4fbebea..c67308118 100644 --- a/examples/tempoGAN/tempoGAN.py +++ b/examples/tempoGAN/tempoGAN.py @@ -13,16 +13,14 @@ # limitations under the License. import os -from os import path as osp import functions as func_module -import hydra import numpy as np import paddle -from omegaconf import DictConfig import ppsci from ppsci.utils import checker +from ppsci.utils import config from ppsci.utils import logger if not checker.dynamic_import_to_globals("hdf5storage"): @@ -32,63 +30,158 @@ ) import hdf5storage +if __name__ == "__main__": + args = config.parse_args() + ppsci.utils.misc.set_random_seed(42) + DATASET_PATH = "./datasets/tempoGAN/2d_train.mat" + DATASET_PATH_VALID = "./datasets/tempoGAN/2d_valid.mat" + OUTPUT_DIR = "./output_tempoGAN/" if args.output_dir is None else args.output_dir -def train(cfg: DictConfig): - ppsci.utils.misc.set_random_seed(cfg.seed) # initialize logger - logger.init_logger("ppsci", osp.join(cfg.output_dir, "train.log"), "info") + logger.init_logger("ppsci", f"{OUTPUT_DIR}/train.log", "info") - gen_funcs = func_module.GenFuncs( - cfg.WEIGHT_GEN, (cfg.WEIGHT_GEN_LAYER if cfg.USE_SPATIALDISC else None) - ) - disc_funcs = func_module.DiscFuncs(cfg.WEIGHT_DISC) - data_funcs = func_module.DataFuncs(cfg.TILE_RATIO) + # initialize parameters and import classes + USE_AMP = True + USE_SPATIALDISC = True + USE_TEMPODISC = True + + weight_gen = [5.0, 0.0, 1.0] # lambda_l1, lambda_l2, lambda_t + weight_gen_layer = ( + [-1e-5, -1e-5, -1e-5, -1e-5, -1e-5] if USE_SPATIALDISC else None + ) # lambda_layer, lambda_layer1, lambda_layer2, lambda_layer3, lambda_layer4 + weight_disc = 1.0 + tile_ratio = 1 + + gen_funcs = func_module.GenFuncs(weight_gen, weight_gen_layer) + dics_funcs = func_module.DiscFuncs(weight_disc) + data_funcs = func_module.DataFuncs(tile_ratio) # load dataset - dataset_train = hdf5storage.loadmat(cfg.DATASET_PATH) - dataset_valid = hdf5storage.loadmat(cfg.DATASET_PATH_VALID) + dataset_train = hdf5storage.loadmat(DATASET_PATH) + dataset_valid = hdf5storage.loadmat(DATASET_PATH_VALID) + + # init Generator params + in_channel = 1 + rb_channel0 = (2, 8, 8) + rb_channel1 = (128, 128, 128) + rb_channel2 = (32, 8, 8) + rb_channel3 = (2, 1, 1) + out_channels_tuple = (rb_channel0, rb_channel1, rb_channel2, rb_channel3) + kernel_sizes_tuple = (((5, 5),) * 2 + ((1, 1),),) * 4 + strides_tuple = ((1, 1, 1),) * 4 + use_bns_tuple = ((True, True, True),) * 3 + ((False, False, False),) + acts_tuple = (("relu", None, None),) * 4 # define Generator model - model_gen = ppsci.arch.Generator(**cfg.MODEL.gen_net) + model_gen = ppsci.arch.Generator( + ("input_gen",), # 'NCHW' + ("output_gen",), + in_channel, + out_channels_tuple, + kernel_sizes_tuple, + strides_tuple, + use_bns_tuple, + acts_tuple, + ) + model_gen.register_input_transform(gen_funcs.transform_in) - disc_funcs.model_gen = model_gen + dics_funcs.model_gen = model_gen model_tuple = (model_gen,) + + # init Discriminators params + in_channel = 2 + in_channel_tempo = 3 + out_channels = (32, 64, 128, 256) + in_shape = np.shape(dataset_train["density_high"][0]) + h, w = in_shape[1] // tile_ratio, in_shape[2] // tile_ratio + down_sample_ratio = 2 ** (len(out_channels) - 1) + fc_channel = int( + out_channels[-1] * (h / down_sample_ratio) * (w / down_sample_ratio) + ) + kernel_sizes = ((4, 4),) * 4 + strides = (2,) * 3 + (1,) + use_bns = (False,) + (True,) * 3 + acts = ("leaky_relu",) * 4 + (None,) + # define Discriminators - if cfg.USE_SPATIALDISC: - model_disc = ppsci.arch.Discriminator(**cfg.MODEL.disc_net) - model_disc.register_input_transform(disc_funcs.transform_in) + if USE_SPATIALDISC: + output_keys_disc = ( + tuple(f"out0_layer{i}" for i in range(4)) + + ("out_disc_from_target",) + + tuple(f"out1_layer{i}" for i in range(4)) + + ("out_disc_from_gen",) + ) + model_disc = ppsci.arch.Discriminator( + ("input_disc_from_target", "input_disc_from_gen"), # 'NCHW' + output_keys_disc, + in_channel, + out_channels, + fc_channel, + kernel_sizes, + strides, + use_bns, + acts, + ) + model_disc.register_input_transform(dics_funcs.transform_in) model_tuple += (model_disc,) # define temporal Discriminators - if cfg.USE_TEMPODISC: - model_disc_tempo = ppsci.arch.Discriminator(**cfg.MODEL.tempo_net) - model_disc_tempo.register_input_transform(disc_funcs.transform_in_tempo) + if USE_TEMPODISC: + output_keys_disc_tempo = ( + tuple(f"out0_tempo_layer{i}" for i in range(4)) + + ("out_disc_tempo_from_target",) + + tuple(f"out1_tempo_layer{i}" for i in range(4)) + + ("out_disc_tempo_from_gen",) + ) + model_disc_tempo = ppsci.arch.Discriminator( + ("input_tempo_disc_from_target", "input_tempo_disc_from_gen"), # 'NCHW' + output_keys_disc_tempo, + in_channel_tempo, + out_channels, + fc_channel, + kernel_sizes, + strides, + use_bns, + acts, + ) + model_disc_tempo.register_input_transform(dics_funcs.transform_in_tempo) model_tuple += (model_disc_tempo,) # define model_list model_list = ppsci.arch.ModelList(model_tuple) + # set training hyper-parameters + ITERS_PER_EPOCH = 2 + EPOCHS = 40000 if args.epochs is None else args.epochs + EPOCHS_GEN = EPOCHS_DISC = EPOCHS_DISC_TEMPO = 1 + BATCH_SIZE = 8 + # initialize Adam optimizer lr_scheduler_gen = ppsci.optimizer.lr_scheduler.Step( - step_size=cfg.TRAIN.epochs // 2, **cfg.TRAIN.lr_scheduler + epochs=EPOCHS, + iters_per_epoch=ITERS_PER_EPOCH, + learning_rate=2e-4, + step_size=EPOCHS // 2, + gamma=0.05, + by_epoch=True, )() optimizer_gen = ppsci.optimizer.Adam(lr_scheduler_gen)((model_gen,)) - if cfg.USE_SPATIALDISC: + if USE_SPATIALDISC: lr_scheduler_disc = ppsci.optimizer.lr_scheduler.Step( - step_size=cfg.TRAIN.epochs // 2, **cfg.TRAIN.lr_scheduler + EPOCHS, ITERS_PER_EPOCH, 2e-4, EPOCHS // 2, 0.05, by_epoch=True )() optimizer_disc = ppsci.optimizer.Adam(lr_scheduler_disc)((model_disc,)) - if cfg.USE_TEMPODISC: + if USE_TEMPODISC: lr_scheduler_disc_tempo = ppsci.optimizer.lr_scheduler.Step( - step_size=cfg.TRAIN.epochs // 2, **cfg.TRAIN.lr_scheduler + EPOCHS, ITERS_PER_EPOCH, 2e-4, EPOCHS // 2, 0.05, by_epoch=True )() optimizer_disc_tempo = ppsci.optimizer.Adam(lr_scheduler_disc_tempo)( (model_disc_tempo,) ) # Generator - # manually build constraint(s) + # maunally build constraint(s) sup_constraint_gen = ppsci.constraint.SupervisedConstraint( { "dataset": { @@ -106,7 +199,7 @@ def train(cfg: DictConfig): }, ), }, - "batch_size": cfg.TRAIN.batch_size.sup_constraint, + "batch_size": BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, @@ -117,7 +210,7 @@ def train(cfg: DictConfig): name="sup_constraint_gen", ) constraint_gen = {sup_constraint_gen.name: sup_constraint_gen} - if cfg.USE_TEMPODISC: + if USE_TEMPODISC: sup_constraint_gen_tempo = ppsci.constraint.SupervisedConstraint( { "dataset": { @@ -135,7 +228,7 @@ def train(cfg: DictConfig): }, ), }, - "batch_size": int(cfg.TRAIN.batch_size.sup_constraint // 3), + "batch_size": int(BATCH_SIZE // 3), "sampler": { "name": "BatchSampler", "drop_last": False, @@ -148,8 +241,8 @@ def train(cfg: DictConfig): constraint_gen[sup_constraint_gen_tempo.name] = sup_constraint_gen_tempo # Discriminators - # manually build constraint(s) - if cfg.USE_SPATIALDISC: + # maunally build constraint(s) + if USE_SPATIALDISC: sup_constraint_disc = ppsci.constraint.SupervisedConstraint( { "dataset": { @@ -176,14 +269,14 @@ def train(cfg: DictConfig): }, ), }, - "batch_size": cfg.TRAIN.batch_size.sup_constraint, + "batch_size": BATCH_SIZE, "sampler": { "name": "BatchSampler", "drop_last": False, "shuffle": False, }, }, - ppsci.loss.FunctionalLoss(disc_funcs.loss_func), + ppsci.loss.FunctionalLoss(dics_funcs.loss_func), name="sup_constraint_disc", ) constraint_disc = { @@ -191,8 +284,8 @@ def train(cfg: DictConfig): } # temporal Discriminators - # manually build constraint(s) - if cfg.USE_TEMPODISC: + # maunally build constraint(s) + if USE_TEMPODISC: sup_constraint_disc_tempo = ppsci.constraint.SupervisedConstraint( { "dataset": { @@ -219,14 +312,14 @@ def train(cfg: DictConfig): }, ), }, - "batch_size": int(cfg.TRAIN.batch_size.sup_constraint // 3), + "batch_size": int(BATCH_SIZE // 3), "sampler": { "name": "BatchSampler", "drop_last": False, "shuffle": False, }, }, - ppsci.loss.FunctionalLoss(disc_funcs.loss_func_tempo), + ppsci.loss.FunctionalLoss(dics_funcs.loss_func_tempo), name="sup_constraint_disc_tempo", ) constraint_disc_tempo = { @@ -237,93 +330,73 @@ def train(cfg: DictConfig): solver_gen = ppsci.solver.Solver( model_list, constraint_gen, - cfg.output_dir, + OUTPUT_DIR, optimizer_gen, lr_scheduler_gen, - cfg.TRAIN.epochs_gen, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - use_amp=cfg.USE_AMP, - amp_level=cfg.TRAIN.amp_level, + EPOCHS_GEN, + ITERS_PER_EPOCH, + eval_during_train=False, + use_amp=USE_AMP, + amp_level="O2", ) - if cfg.USE_SPATIALDISC: + if USE_SPATIALDISC: solver_disc = ppsci.solver.Solver( model_list, constraint_disc, - cfg.output_dir, + OUTPUT_DIR, optimizer_disc, lr_scheduler_disc, - cfg.TRAIN.epochs_disc, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - use_amp=cfg.USE_AMP, - amp_level=cfg.TRAIN.amp_level, + EPOCHS_DISC, + ITERS_PER_EPOCH, + eval_during_train=False, + use_amp=USE_AMP, + amp_level="O2", ) - if cfg.USE_TEMPODISC: + if USE_TEMPODISC: solver_disc_tempo = ppsci.solver.Solver( model_list, constraint_disc_tempo, - cfg.output_dir, + OUTPUT_DIR, optimizer_disc_tempo, lr_scheduler_disc_tempo, - cfg.TRAIN.epochs_disc_tempo, - cfg.TRAIN.iters_per_epoch, - eval_during_train=cfg.TRAIN.eval_during_train, - use_amp=cfg.USE_AMP, - amp_level=cfg.TRAIN.amp_level, + EPOCHS_DISC_TEMPO, + ITERS_PER_EPOCH, + eval_during_train=False, + use_amp=USE_AMP, + amp_level="O2", ) PRED_INTERVAL = 200 - for i in range(1, cfg.TRAIN.epochs + 1): + for i in range(1, EPOCHS + 1): logger.message(f"\nEpoch: {i}\n") # plotting during training - if i == 1 or i % PRED_INTERVAL == 0 or i == cfg.TRAIN.epochs: + if i == 1 or i % PRED_INTERVAL == 0 or i == EPOCHS: func_module.predict_and_save_plot( - cfg.output_dir, i, solver_gen, dataset_valid, cfg.TILE_RATIO + OUTPUT_DIR, i, solver_gen, dataset_valid, tile_ratio ) - disc_funcs.model_gen = model_gen + dics_funcs.model_gen = model_gen # train disc, input: (x,y,G(x)) - if cfg.USE_SPATIALDISC: + if USE_SPATIALDISC: solver_disc.train() # train disc tempo, input: (y_3,G(x)_3) - if cfg.USE_TEMPODISC: + if USE_TEMPODISC: solver_disc_tempo.train() # train gen, input: (x,) solver_gen.train() - -def evaluate(cfg: DictConfig): ############### evaluation after training ############### img_target = ( - func_module.get_image_array( - os.path.join(cfg.output_dir, "predict", "target.png") - ) + func_module.get_image_array(os.path.join(OUTPUT_DIR, "predict", "target.png")) / 255.0 ) img_pred = ( func_module.get_image_array( - os.path.join( - cfg.output_dir, "predict", f"pred_epoch_{cfg.TRAIN.epochs}.png" - ) + os.path.join(OUTPUT_DIR, "predict", f"pred_epoch_{EPOCHS}.png") ) / 255.0 ) eval_mse, eval_psnr, eval_ssim = func_module.evaluate_img(img_target, img_pred) logger.message(f"MSE: {eval_mse}, PSNR: {eval_psnr}, SSIM: {eval_ssim}") - - -@hydra.main(version_base=None, config_path="./conf", config_name="tempogan.yaml") -def main(cfg: DictConfig): - if cfg.mode == "train": - train(cfg) - elif cfg.mode == "eval": - evaluate(cfg) - else: - raise ValueError(f"cfg.mode should in ['train', 'eval'], but got '{cfg.mode}'") - - -if __name__ == "__main__": - main() diff --git a/jointContribution/XPINNs/XPINN_2D_PoissonsEqn.py b/jointContribution/XPINNs/XPINN_2D_PoissonsEqn.py index d9fe1b090..78e9f4a21 100755 --- a/jointContribution/XPINNs/XPINN_2D_PoissonsEqn.py +++ b/jointContribution/XPINNs/XPINN_2D_PoissonsEqn.py @@ -9,7 +9,6 @@ from matplotlib import gridspec from matplotlib import patches from matplotlib import tri -from paddle import nn import ppsci @@ -20,7 +19,7 @@ paddle.seed(1234) -class XPINN(nn.Layer): +class XPINN(paddle.nn.Layer): # Initialize the class def __init__(self, layer_list): super().__init__() @@ -131,13 +130,13 @@ def initialize_nn(self, layers, name_prefix): shape=[1, layers[l + 1]], dtype="float64", is_bias=True, - default_initializer=nn.initializer.Constant(0.0), + default_initializer=paddle.nn.initializer.Constant(0.0), ) amplitude = self.create_parameter( shape=[1], dtype="float64", is_bias=True, - default_initializer=nn.initializer.Constant(0.05), + default_initializer=paddle.nn.initializer.Constant(0.05), ) self.add_parameter(name_prefix + "_w_" + str(l), weight) @@ -154,7 +153,8 @@ def w_init(self, size): xavier_stddev = np.sqrt(2 / (in_dim + out_dim)) param = paddle.empty(size, "float64") param = ppsci.utils.initializer.trunc_normal_(param, 0.0, xavier_stddev) - return nn.initializer.Assign(param) + # TODO: Truncated normal and assign support float64 + return lambda p_ten, _: p_ten.set_value(param) def neural_net_tanh(self, x, weights, biases, amplitudes): num_layers = len(weights) + 1 @@ -479,7 +479,8 @@ def predict(self, x_star1, x_star2, x_star3): print("Error u_total: %e" % (error_u_total)) ############################# Plotting ############################### - os.makedirs("./target", exist_ok=True) + if not os.path.exists("./target"): + os.mkdir("./target") fig, ax = plotting.newfig(1.0, 1.1) plt.plot(range(1, max_iter + 1, 20), mse_hist1, "r-", linewidth=1, label="Sub-Net1") plt.plot( diff --git a/ppsci/arch/__init__.py b/ppsci/arch/__init__.py index f418e225f..986e31893 100644 --- a/ppsci/arch/__init__.py +++ b/ppsci/arch/__init__.py @@ -12,12 +12,9 @@ # See the License for the specific language governing permissions and # limitations under the License. -from __future__ import annotations - import copy from ppsci.arch.base import Arch # isort:skip -from ppsci.arch.amgnet import AMGNet # isort:skip from ppsci.arch.mlp import MLP # isort:skip from ppsci.arch.deeponet import DeepONet # isort:skip from ppsci.arch.embedding_koopman import LorenzEmbedding # isort:skip @@ -25,21 +22,17 @@ from ppsci.arch.embedding_koopman import CylinderEmbedding # isort:skip from ppsci.arch.gan import Generator # isort:skip from ppsci.arch.gan import Discriminator # isort:skip -from ppsci.arch.phylstm import DeepPhyLSTM # isort:skip from ppsci.arch.physx_transformer import PhysformerGPT2 # isort:skip from ppsci.arch.model_list import ModelList # isort:skip from ppsci.arch.afno import AFNONet # isort:skip from ppsci.arch.afno import PrecipNet # isort:skip -from ppsci.arch.unetex import UNetEx # isort:skip from ppsci.utils import logger # isort:skip __all__ = [ "Arch", - "AMGNet", "MLP", "DeepONet", - "DeepPhyLSTM", "LorenzEmbedding", "RosslerEmbedding", "CylinderEmbedding", @@ -49,7 +42,6 @@ "ModelList", "AFNONet", "PrecipNet", - "UNetEx", "build_model", ] diff --git a/ppsci/arch/activation.py b/ppsci/arch/activation.py index 73ac202fc..627781122 100644 --- a/ppsci/arch/activation.py +++ b/ppsci/arch/activation.py @@ -97,7 +97,7 @@ def forward(self, x): @staticmethod def init_for_first_layer(layer: nn.Linear): - """Initialization only for first hidden layer. + """Initialzation only for first hidden layer. ref: https://github.com/vsitzmann/siren/blob/master/modules.py#L630 """ if not isinstance(layer, nn.Linear): @@ -112,7 +112,7 @@ def init_for_first_layer(layer: nn.Linear): @staticmethod def init_for_hidden_layer(layer: nn.Linear, w0: float = 30): - """Initialization for hidden layer except first layer. + """Initialzation for hidden layer except first layer. ref: https://github.com/vsitzmann/siren/blob/master/modules.py#L622 """ if not isinstance(layer, nn.Linear): diff --git a/ppsci/arch/base.py b/ppsci/arch/base.py index 5d173cf00..cf4d79dc5 100644 --- a/ppsci/arch/base.py +++ b/ppsci/arch/base.py @@ -28,9 +28,6 @@ class Arch(nn.Layer): """Base class for Network.""" - input_keys: Tuple[str, ...] - output_keys: Tuple[str, ...] - def __init__(self, *args, **kwargs): super().__init__(*args, **kwargs) self._input_transform: Callable[ @@ -68,7 +65,7 @@ def concat_to_tensor( Args: data_dict (Dict[str, paddle.Tensor]): Dict contains tensor. keys (Tuple[str, ...]): Keys tensor fetched from. - axis (int, optional): Axis concatenate at. Defaults to -1. + axis (int, optional): Axis concate at. Defaults to -1. Returns: Tuple[paddle.Tensor, ...]: Concatenated tensor. diff --git a/ppsci/arch/embedding_koopman.py b/ppsci/arch/embedding_koopman.py index a4c852da3..5bae9ce2b 100644 --- a/ppsci/arch/embedding_koopman.py +++ b/ppsci/arch/embedding_koopman.py @@ -69,11 +69,11 @@ def __init__( self.hidden_size = hidden_size self.embed_size = embed_size - # build observable network + # build observable netowrk self.encoder_net = self.build_encoder(input_size, hidden_size, embed_size, drop) # build koopman operator self.k_diag, self.k_ut = self.build_koopman_operator(embed_size) - # build recovery network + # build recovery netowrk self.decoder_net = self.build_decoder(input_size, hidden_size, embed_size) mean = [0.0, 0.0, 0.0] if mean is None else mean diff --git a/ppsci/arch/gan.py b/ppsci/arch/gan.py index e78a291fe..3c7ec2c19 100644 --- a/ppsci/arch/gan.py +++ b/ppsci/arch/gan.py @@ -365,11 +365,11 @@ def split_to_dict( } Args: - data_list (List[paddle.Tensor]): The data to be split. It should be a list of tensor(s), but not a paddle.Tensor. + data_list (List[paddle.Tensor]): The data to be splited. It should be a list of tensor(s), but not a paddle.Tensor. keys (Tuple[str, ...]): Keys of outputs. Returns: - Dict[str, paddle.Tensor]: Dict with split data. + Dict[str, paddle.Tensor]: Dict with splited data. """ if len(keys) == 1: return {keys[0]: data_list[0]} diff --git a/ppsci/arch/mlp.py b/ppsci/arch/mlp.py index b4e5f9858..c874669d2 100644 --- a/ppsci/arch/mlp.py +++ b/ppsci/arch/mlp.py @@ -118,8 +118,8 @@ def __init__( if activation != "stan" else act_mod.get_activation(activation)(_size) ) - # special initialization for certain activation - # TODO: Adapt code below to a more elegant style + # spetial initialization for certain activation + # TODO: Adapt code below to a more elegent style if activation == "siren": if i == 0: act_mod.Siren.init_for_first_layer(self.linears[-1]) diff --git a/ppsci/arch/model_list.py b/ppsci/arch/model_list.py index c5faa4baa..f463f1722 100644 --- a/ppsci/arch/model_list.py +++ b/ppsci/arch/model_list.py @@ -25,7 +25,7 @@ class ModelList(base.Arch): """ModelList layer which wrap more than one model that shares inputs. Args: - model_list (Tuple[base.Arch, ...]): Model(s) nested in tuple. + model_list (Tuple[base.Arch, ...]): Model(s) nesteed in tuple. Examples: >>> import ppsci @@ -39,9 +39,6 @@ def __init__( model_list: Tuple[base.Arch, ...], ): super().__init__() - self.input_keys = sum([model.input_keys for model in model_list], ()) - self.input_keys = set(self.input_keys) - output_keys_set = set() for model in model_list: if len(output_keys_set & set(model.output_keys)): @@ -50,7 +47,6 @@ def __init__( f"but got duplicate keys: {output_keys_set & set(model.output_keys)}" ) output_keys_set = output_keys_set | set(model.output_keys) - self.output_keys = tuple(output_keys_set) self.model_list = nn.LayerList(model_list) diff --git a/ppsci/arch/physx_transformer.py b/ppsci/arch/physx_transformer.py index 014cc0e5f..a3fdb8120 100644 --- a/ppsci/arch/physx_transformer.py +++ b/ppsci/arch/physx_transformer.py @@ -38,7 +38,7 @@ class MaskedAttention(nn.Layer): Args: embed_dim (int): The expected feature size in the input and output. - num_ctx (int): Context length of block. + num_ctx (int): Contex length of block. num_heads (int): The number of heads in multi-head attention. attn_drop (float, optional): The dropout probability used on attention weights to drop some attention targets. Defaults to 0. @@ -188,7 +188,7 @@ class Block(nn.Layer): masked self-attention, layer norm and fully connected layer. Args: - num_ctx (int): Context length of block + num_ctx (int): Contex length of block embed_size (int): The number of embedding size. num_heads (int): The number of heads in multi-head attention. attn_pdrop (float): The dropout probability used on attention @@ -244,7 +244,7 @@ class PhysformerGPT2(base.Arch): input_keys (Tuple[str, ...]): Input keys, such as ("embeds",). output_keys (Tuple[str, ...]): Output keys, such as ("pred_embeds",). num_layers (int): Number of transformer layers. - num_ctx (int): Context length of block. + num_ctx (int): Contex length of block. embed_size (int): The number of embedding size. num_heads (int): The number of heads in multi-head attention. embd_pdrop (float, optional): The dropout probability used on embedding features. Defaults to 0.0. @@ -351,7 +351,7 @@ def generate(self, x, max_length=256): def forward_tensor(self, x): position_embeds = self.get_position_embed(x) - # Combine input embedding, position embedding + # Combine input embedding, position embeding hidden_states = x + position_embeds hidden_states = self.drop(hidden_states) diff --git a/ppsci/autodiff/ad.py b/ppsci/autodiff/ad.py index f7f442afb..6eec7eebc 100644 --- a/ppsci/autodiff/ad.py +++ b/ppsci/autodiff/ad.py @@ -18,7 +18,6 @@ from __future__ import annotations -from typing import Dict from typing import Optional import paddle @@ -43,15 +42,9 @@ def __init__(self, ys: "paddle.Tensor", xs: "paddle.Tensor"): self.dim_y = ys.shape[1] self.dim_x = xs.shape[1] - self.J: Dict[str, paddle.Tensor] = {} + self.J = {} - def __call__( - self, - i: int = 0, - j: Optional[int] = None, - retain_graph: Optional[bool] = None, - create_graph: bool = True, - ) -> "paddle.Tensor": + def __call__(self, i: int = 0, j: Optional[int] = None) -> "paddle.Tensor": """Returns J[`i`][`j`]. If `j` is ``None``, returns the gradient of y_i, i.e., J[i]. """ @@ -62,9 +55,7 @@ def __call__( # Compute J[i] if i not in self.J: y = self.ys[:, i : i + 1] if self.dim_y > 1 else self.ys - self.J[i] = paddle.grad( - y, self.xs, retain_graph=retain_graph, create_graph=create_graph - )[0] + self.J[i] = paddle.grad(y, self.xs, create_graph=True)[0] return self.J[i] if (j is None or self.dim_x == 1) else self.J[i][:, j : j + 1] @@ -90,8 +81,6 @@ def __call__( xs: "paddle.Tensor", i: int = 0, j: Optional[int] = None, - retain_graph: Optional[bool] = None, - create_graph: bool = True, ) -> "paddle.Tensor": """Compute jacobians for given ys and xs. @@ -100,15 +89,6 @@ def __call__( xs (paddle.Tensor): Input tensor. i (int, optional): i-th output variable. Defaults to 0. j (Optional[int]): j-th input variable. Defaults to None. - retain_graph (Optional[bool]): whether to retain the forward graph which - is used to calculate the gradient. When it is True, the graph would - be retained, in which way users can calculate backward twice for the - same graph. When it is False, the graph would be freed. Default None, - which means it is equal to `create_graph`. - create_graph (bool, optional): whether to create the gradient graphs of - the computing process. When it is True, higher order derivatives are - supported to compute; when it is False, the gradient graphs of the - computing process would be discarded. Default False. Returns: paddle.Tensor: Jacobian matrix of ys[i] to xs[j]. @@ -124,7 +104,7 @@ def __call__( key = (ys, xs) if key not in self.Js: self.Js[key] = _Jacobian(ys, xs) - return self.Js[key](i, j, retain_graph, create_graph) + return self.Js[key](i, j) def _clear(self): """Clear cached Jacobians.""" @@ -176,21 +156,12 @@ def __init__( component = 0 if grad_y is None: - # `create_graph` of first order(jacobian) should be `True` in _Hessian. - grad_y = jacobian( - ys, xs, i=component, j=None, retain_graph=None, create_graph=True - ) + grad_y = jacobian(ys, xs, i=component, j=None) self.H = _Jacobian(grad_y, xs) - def __call__( - self, - i: int = 0, - j: int = 0, - retain_graph: Optional[bool] = None, - create_graph: bool = True, - ): + def __call__(self, i: int = 0, j: int = 0): """Returns H[`i`][`j`].""" - return self.H(i, j, retain_graph, create_graph) + return self.H(i, j) class Hessians: @@ -216,8 +187,6 @@ def __call__( i: int = 0, j: int = 0, grad_y: Optional["paddle.Tensor"] = None, - retain_graph: Optional[bool] = None, - create_graph: bool = True, ) -> "paddle.Tensor": """Compute hessian matrix for given ys and xs. @@ -231,15 +200,6 @@ def __call__( j (int, optional): j-th input variable. Defaults to 0. grad_y (Optional[paddle.Tensor]): The gradient of `y` w.r.t. `xs`. Provide `grad_y` if known to avoid duplicate computation. Defaults to None. - retain_graph (Optional[bool]): whether to retain the forward graph which - is used to calculate the gradient. When it is True, the graph would - be retained, in which way users can calculate backward twice for the - same graph. When it is False, the graph would be freed. Default None, - which means it is equal to `create_graph`. - create_graph (bool, optional): whether to create the gradient graphs of - the computing process. When it is True, higher order derivatives are - supported to compute; when it is False, the gradient graphs of the - computing process would be discarded. Default False. Returns: paddle.Tensor: Hessian matrix. @@ -255,7 +215,7 @@ def __call__( key = (ys, xs, component) if key not in self.Hs: self.Hs[key] = _Hessian(ys, xs, component=component, grad_y=grad_y) - return self.Hs[key](i, j, retain_graph, create_graph) + return self.Hs[key](i, j) def _clear(self): """Clear cached Hessians.""" diff --git a/ppsci/constraint/integral_constraint.py b/ppsci/constraint/integral_constraint.py index f9cb22674..1b0205be6 100644 --- a/ppsci/constraint/integral_constraint.py +++ b/ppsci/constraint/integral_constraint.py @@ -18,7 +18,6 @@ from typing import Any from typing import Callable from typing import Dict -from typing import List from typing import Optional from typing import Union @@ -100,7 +99,7 @@ def __init__( criteria = eval(criteria) # prepare input - input_list: List[Dict[str, np.ndarray]] = [] + input_list = [] for _ in range( dataloader_cfg["batch_size"] * dataloader_cfg["iters_per_epoch"] ): diff --git a/ppsci/data/__init__.py b/ppsci/data/__init__.py index a1933cfb7..f39a663ff 100644 --- a/ppsci/data/__init__.py +++ b/ppsci/data/__init__.py @@ -56,7 +56,7 @@ def worker_init_fn(worker_id, num_workers, rank, base_seed): def build_dataloader(_dataset, cfg): world_size = dist.get_world_size() - # just return IterableDataset as dataloader + # just return IterableDataset as datalaoder if isinstance(_dataset, io.IterableDataset): if world_size > 1: raise ValueError( @@ -67,34 +67,24 @@ def build_dataloader(_dataset, cfg): cfg = copy.deepcopy(cfg) # build sampler - sampler_cfg = cfg.pop("sampler", None) - if sampler_cfg is not None: - sampler_cls = sampler_cfg.pop("name") - if sampler_cls == "BatchSampler": - if world_size > 1: - sampler_cls = "DistributedBatchSampler" - logger.warning( - f"Automatically use 'DistributedBatchSampler' instead of " - f"'BatchSampler' when world_size({world_size}) > 1" - ) - - sampler_cfg["batch_size"] = cfg["batch_size"] - sampler = getattr(io, sampler_cls)(_dataset, **sampler_cfg) - else: - if cfg["batch_size"] != 1: - raise ValueError( - f"`batch_size` should be 1 when sampler config is None, but got {cfg['batch_size']}." + sampler_cfg = cfg.pop("sampler") + sampler_cls = sampler_cfg.pop("name") + if sampler_cls == "BatchSampler": + if world_size > 1: + sampler_cls = "DistributedBatchSampler" + logger.warning( + f"Automatically use 'DistributedBatchSampler' instead of " + f"'BatchSampler' when world_size({world_size}) > 1" ) - logger.warning( - "`batch_size` is set to 1 as neither sampler config or batch_size is set." - ) - sampler = None + + sampler_cfg["batch_size"] = cfg["batch_size"] + sampler = getattr(io, sampler_cls)(_dataset, **sampler_cfg) # build collate_fn if specified batch_transforms_cfg = cfg.pop("batch_transforms", None) collate_fn = None - if isinstance(batch_transforms_cfg, (list, tuple)): + if isinstance(batch_transforms_cfg, dict) and batch_transforms_cfg: collate_fn = batch_transform.build_batch_transforms(batch_transforms_cfg) # build init function @@ -106,33 +96,15 @@ def build_dataloader(_dataset, cfg): ) # build dataloader - if getattr(_dataset, "use_pgl", False): - # Use special dataloader from "Paddle Graph Learning" toolkit. - try: - from pgl.utils import data as pgl_data - except ModuleNotFoundError as e: - logger.error("Please install pgl with `pip install pgl`.") - raise ModuleNotFoundError(str(e)) - - collate_fn = batch_transform.default_collate_fn - dataloader_ = pgl_data.Dataloader( - dataset=_dataset, - batch_size=cfg["batch_size"], - drop_last=sampler_cfg.get("drop_last", False), - shuffle=sampler_cfg.get("shuffle", False), - num_workers=cfg.get("num_workers", 1), - collate_fn=collate_fn, - ) - else: - dataloader_ = io.DataLoader( - dataset=_dataset, - places=device.get_device(), - batch_sampler=sampler, - collate_fn=collate_fn, - num_workers=cfg.get("num_workers", 1), - use_shared_memory=cfg.get("use_shared_memory", False), - worker_init_fn=init_fn, - ) + dataloader_ = io.DataLoader( + dataset=_dataset, + places=device.get_device(), + batch_sampler=sampler, + collate_fn=collate_fn, + num_workers=cfg.get("num_workers", 0), + use_shared_memory=cfg.get("use_shared_memory", False), + worker_init_fn=init_fn, + ) if len(dataloader_) == 0: raise ValueError( diff --git a/ppsci/data/dataset/__init__.py b/ppsci/data/dataset/__init__.py index 997573502..58fb2c1f8 100644 --- a/ppsci/data/dataset/__init__.py +++ b/ppsci/data/dataset/__init__.py @@ -13,14 +13,11 @@ # limitations under the License. import copy -from typing import TYPE_CHECKING -from ppsci.data.dataset.airfoil_dataset import MeshAirfoilDataset from ppsci.data.dataset.array_dataset import IterableNamedArrayDataset from ppsci.data.dataset.array_dataset import NamedArrayDataset from ppsci.data.dataset.csv_dataset import CSVDataset from ppsci.data.dataset.csv_dataset import IterableCSVDataset -from ppsci.data.dataset.cylinder_dataset import MeshCylinderDataset from ppsci.data.dataset.era5_dataset import ERA5Dataset from ppsci.data.dataset.era5_dataset import ERA5SampledDataset from ppsci.data.dataset.mat_dataset import IterableMatDataset @@ -34,9 +31,6 @@ from ppsci.data.process import transform from ppsci.utils import logger -if TYPE_CHECKING: - from paddle import io - __all__ = [ "IterableNamedArrayDataset", "NamedArrayDataset", @@ -52,13 +46,11 @@ "LorenzDataset", "RosslerDataset", "VtuDataset", - "MeshAirfoilDataset", - "MeshCylinderDataset", "build_dataset", ] -def build_dataset(cfg) -> "io.Dataset": +def build_dataset(cfg): """Build dataset Args: diff --git a/ppsci/data/dataset/array_dataset.py b/ppsci/data/dataset/array_dataset.py index 91cdd6a7e..7f0621702 100644 --- a/ppsci/data/dataset/array_dataset.py +++ b/ppsci/data/dataset/array_dataset.py @@ -62,10 +62,9 @@ def __getitem__(self, idx): label_item = {key: value[idx] for key, value in self.label.items()} weight_item = {key: value[idx] for key, value in self.weight.items()} + # TODO(sensen): Transforms may be applied on label and weight. if self.transforms is not None: - input_item, label_item, weight_item = self.transforms( - (input_item, label_item, weight_item) - ) + input_item = self.transforms(input_item) return (input_item, label_item, weight_item) @@ -118,10 +117,7 @@ def num_samples(self): def __iter__(self): if callable(self.transforms): - input_, label_, weight_ = self.transforms( - self.input, self.label, self.weight - ) - yield input_, label_, weight_ + yield self.transforms(self.input), self.label, self.weight else: yield self.input, self.label, self.weight diff --git a/ppsci/data/dataset/csv_dataset.py b/ppsci/data/dataset/csv_dataset.py index 22e5f0f8a..eec11e3b9 100644 --- a/ppsci/data/dataset/csv_dataset.py +++ b/ppsci/data/dataset/csv_dataset.py @@ -138,10 +138,9 @@ def __getitem__(self, idx): label_item = {key: value[idx] for key, value in self.label.items()} weight_item = {key: value[idx] for key, value in self.weight.items()} + # TODO(sensen): Transforms may be applied on label and weight. if self.transforms is not None: - input_item, label_item, weight_item = self.transforms( - (input_item, label_item, weight_item) - ) + input_item = self.transforms(input_item) return (input_item, label_item, weight_item) diff --git a/ppsci/data/dataset/mat_dataset.py b/ppsci/data/dataset/mat_dataset.py index f681b5b44..344efb3d7 100644 --- a/ppsci/data/dataset/mat_dataset.py +++ b/ppsci/data/dataset/mat_dataset.py @@ -138,10 +138,9 @@ def __getitem__(self, idx): label_item = {key: value[idx] for key, value in self.label.items()} weight_item = {key: value[idx] for key, value in self.weight.items()} + # TODO(sensen): Transforms may be applied on label and weight. if self.transforms is not None: - input_item, label_item, weight_item = self.transforms( - (input_item, label_item, weight_item) - ) + input_item = self.transforms(input_item) return (input_item, label_item, weight_item) diff --git a/ppsci/data/dataset/npz_dataset.py b/ppsci/data/dataset/npz_dataset.py index 6be0a1720..9f5526e96 100644 --- a/ppsci/data/dataset/npz_dataset.py +++ b/ppsci/data/dataset/npz_dataset.py @@ -136,10 +136,9 @@ def __getitem__(self, idx): label_item = {key: value[idx] for key, value in self.label.items()} weight_item = {key: value[idx] for key, value in self.weight.items()} + # TODO(sensen): Transforms may be applied on label and weight. if self.transforms is not None: - input_item, label_item, weight_item = self.transforms( - (input_item, label_item, weight_item) - ) + input_item = self.transforms(input_item) return (input_item, label_item, weight_item) diff --git a/ppsci/data/dataset/vtu_dataset.py b/ppsci/data/dataset/vtu_dataset.py index 4a454a1e9..ef94cdc36 100644 --- a/ppsci/data/dataset/vtu_dataset.py +++ b/ppsci/data/dataset/vtu_dataset.py @@ -14,7 +14,6 @@ from __future__ import annotations -from typing import Dict from typing import Optional from typing import Tuple @@ -32,9 +31,9 @@ class VtuDataset(io.Dataset): file_path (str): *.vtu file path. input_keys (Optional[Tuple[str, ...]]): Tuple of input keys. Defaults to None. label_keys (Optional[Tuple[str, ...]]): Tuple of label keys. Defaults to None. - time_step (Optional[int]): Time step with unit second. Defaults to None. + time_step (int): Time step with unit second. time_index (Optional[Tuple[int, ...]]): Time index tuple in increasing order. - labels (Optional[Dict[str, float]]): Temporary variable for [load_vtk_with_time_file]. + labels : Temporary variable for [load_vtk_with_time_file]. transforms (vision.Compose, optional): Compose object contains sample wise. transform(s). """ @@ -44,9 +43,9 @@ def __init__( file_path: str, input_keys: Optional[Tuple[str, ...]] = None, label_keys: Optional[Tuple[str, ...]] = None, - time_step: Optional[int] = None, + time_step: int = None, time_index: Optional[Tuple[int, ...]] = None, - labels: Optional[Dict[str, float]] = None, + labels=None, transforms: Optional[vision.Compose] = None, ): super().__init__() diff --git a/ppsci/data/process/batch_transform/__init__.py b/ppsci/data/process/batch_transform/__init__.py index 4f546f9a0..2887aa027 100644 --- a/ppsci/data/process/batch_transform/__init__.py +++ b/ppsci/data/process/batch_transform/__init__.py @@ -22,22 +22,14 @@ import numpy as np import paddle -try: - import pgl -except ModuleNotFoundError: - pass - from ppsci.data.process import transform -__all__ = ["build_batch_transforms", "default_collate_fn"] +__all__ = ["build_batch_transforms"] def default_collate_fn(batch: List[Any]) -> Any: """Default_collate_fn for paddle dataloader. - NOTE: This `default_collate_fn` is different from official `default_collate_fn` - which specially adapt case where sample is `None` and `pgl.Graph`. - ref: https://github.com/PaddlePaddle/Paddle/blob/develop/python/paddle/io/dataloader/collate.py#L25 Args: @@ -47,9 +39,7 @@ def default_collate_fn(batch: List[Any]) -> Any: Any: Collated batch data. """ sample = batch[0] - if sample is None: - return None - elif isinstance(sample, np.ndarray): + if isinstance(sample, np.ndarray): batch = np.stack(batch, axis=0) return batch elif isinstance(sample, (paddle.Tensor, paddle.framework.core.eager.Tensor)): @@ -64,23 +54,12 @@ def default_collate_fn(batch: List[Any]) -> Any: elif isinstance(sample, Sequence): sample_fields_num = len(sample) if not all(len(sample) == sample_fields_num for sample in iter(batch)): - raise RuntimeError("Fields number not same among samples in a batch") + raise RuntimeError("fileds number not same among samples in a batch") return [default_collate_fn(fields) for fields in zip(*batch)] - elif str(type(sample)) == "": - # use str(type()) instead of isinstance() in case of pgl is not installed. - graph = pgl.Graph(num_nodes=sample.num_nodes, edges=sample.edges) - graph.x = np.concatenate([g.x for g in batch]) - graph.y = np.concatenate([g.y for g in batch]) - graph.edge_index = np.concatenate([g.edge_index for g in batch], axis=1) - graph.edge_attr = np.concatenate([g.edge_attr for g in batch]) - graph.pos = np.concatenate([g.pos for g in batch]) - graph.tensor() - graph.shape = [len(batch)] - return graph raise TypeError( - "batch data can only contains: paddle.Tensor, numpy.ndarray, " - f"dict, list, number, None, pgl.Graph, but got {type(sample)}" + "batch data can only contains: tensor, numpy.ndarray, " + f"dict, list, number, None, but got {type(sample)}" ) @@ -89,7 +68,7 @@ def build_batch_transforms(cfg): batch_transforms = transform.build_transforms(cfg) def collate_fn_batch_transforms(batch: List[Any]): - # apply batch transform on separate data + # apply batch transform on uncollated data batch = batch_transforms(batch) # then do collate return default_collate_fn(batch) diff --git a/ppsci/data/process/transform/__init__.py b/ppsci/data/process/transform/__init__.py index f5a4baa28..b5bd7cfd0 100644 --- a/ppsci/data/process/transform/__init__.py +++ b/ppsci/data/process/transform/__init__.py @@ -12,10 +12,8 @@ # See the License for the specific language governing permissions and # limitations under the License. +# from ppsci.data.process.postprocess import * import copy -import traceback -from typing import Any -from typing import Tuple from paddle import vision @@ -39,27 +37,9 @@ ] -class Compose(vision.Compose): - """Custom Compose for multiple items in given data.""" - - def __call__(self, *data: Tuple[Any, ...]): - for f in self.transforms: - try: - # NOTE: This is different from vision.Compose to allow receive multiple data items - data = f(*data) - except Exception as e: - stack_info = traceback.format_exc() - print( - f"fail to perform transform [{f}] with error: " - f"{e} and stack:\n{str(stack_info)}" - ) - raise e - return data - - def build_transforms(cfg): if not cfg: - return Compose([]) + return vision.Compose([]) cfg = copy.deepcopy(cfg) transform_list = [] @@ -69,4 +49,4 @@ def build_transforms(cfg): transform = eval(transform_cls)(**transform_cfg) transform_list.append(transform) - return Compose(transform_list) + return vision.Compose(transform_list) diff --git a/ppsci/data/process/transform/preprocess.py b/ppsci/data/process/transform/preprocess.py index 737d53ad8..0376c6a76 100644 --- a/ppsci/data/process/transform/preprocess.py +++ b/ppsci/data/process/transform/preprocess.py @@ -37,12 +37,11 @@ class Translate: def __init__(self, offset: Dict[str, float]): self.offset = offset - def __call__(self, input_dict, label_dict, weight_dict): - input_dict_copy = {**input_dict} + def __call__(self, data_dict): for key in self.offset: - if key in input_dict: - input_dict_copy[key] += self.offset[key] - return input_dict_copy, label_dict, weight_dict + if key in data_dict: + data_dict[key] += self.offset[key] + return data_dict class Scale: @@ -60,20 +59,19 @@ class Scale: def __init__(self, scale: Dict[str, float]): self.scale = scale - def __call__(self, input_dict, label_dict, weight_dict): - input_dict_copy = {**input_dict} + def __call__(self, data_dict): for key in self.scale: - if key in input_dict: - input_dict_copy[key] *= self.scale[key] - return input_dict_copy, label_dict, weight_dict + if key in data_dict: + data_dict[key] *= self.scale[key] + return data_dict class Normalize: """Normalize data class. Args: - mean (Union[np.ndarray, Tuple[float, ...]]): Mean of training dataset. - std (Union[np.ndarray, Tuple[float, ...]]): Standard Deviation of training dataset. + mean (Union[np.array, Tuple[float, ...]]): Mean of training dataset. + std (Union[np.array, Tuple[float, ...]]): Standard Deviation of training dataset. apply_keys (Tuple[str, ...], optional): Which data is the normalization method applied to. Defaults to ("input", "label"). Examples: @@ -83,8 +81,8 @@ class Normalize: def __init__( self, - mean: Union[np.ndarray, Tuple[float, ...]], - std: Union[np.ndarray, Tuple[float, ...]], + mean: Union[np.array, Tuple[float, ...]], + std: Union[np.array, Tuple[float, ...]], apply_keys: Tuple[str, ...] = ("input", "label"), ): if len(apply_keys) == 0 or len(set(apply_keys) | {"input", "label"}) > 2: @@ -95,16 +93,15 @@ def __init__( self.std = std self.apply_keys = apply_keys - def __call__(self, input_item, label_item, weight_item): - input_item_copy = {**input_item} - label_item_copy = {**label_item} + def __call__(self, data): + input_item, label_item, weight_item = data if "input" in self.apply_keys: - for key, value in input_item_copy.items(): - input_item_copy[key] = (value - self.mean) / self.std + for key, value in input_item.items(): + input_item[key] = (value - self.mean) / self.std if "label" in self.apply_keys: - for key, value in label_item_copy.items(): - label_item_copy[key] = (value - self.mean) / self.std - return input_item_copy, label_item_copy, weight_item + for key, value in label_item.items(): + label_item[key] = (value - self.mean) / self.std + return input_item, label_item, weight_item class Log1p: @@ -131,16 +128,15 @@ def __init__( self.scale = scale self.apply_keys = apply_keys - def __call__(self, input_item, label_item, weight_item): - input_item_copy = {**input_item} - label_item_copy = {**label_item} + def __call__(self, data): + input_item, label_item, weight_item = data if "input" in self.apply_keys: - for key, value in input_item_copy.items(): - input_item_copy[key] = np.log1p(value / self.scale) + for key, value in input_item.items(): + input_item[key] = np.log1p(value / self.scale) if "label" in self.apply_keys: - for key, value in label_item_copy.items(): - label_item_copy[key] = np.log1p(value / self.scale) - return input_item_copy, label_item_copy, weight_item + for key, value in label_item.items(): + label_item[key] = np.log1p(value / self.scale) + return input_item, label_item, weight_item class CropData: @@ -170,24 +166,23 @@ def __init__( self.xmax = xmax self.apply_keys = apply_keys - def __call__(self, input_item, label_item, weight_item): - input_item_copy = {**input_item} - label_item_copy = {**label_item} + def __call__(self, data): + input_item, label_item, weight_item = data if "input" in self.apply_keys: - for key, value in input_item_copy.items(): - input_item_copy[key] = value[ + for key, value in input_item.items(): + input_item[key] = value[ :, self.xmin[0] : self.xmax[0], self.xmin[1] : self.xmax[1] ] if "label" in self.apply_keys: - for key, value in label_item_copy.items(): - label_item_copy[key] = value[ + for key, value in label_item.items(): + label_item[key] = value[ :, self.xmin[0] : self.xmax[0], self.xmin[1] : self.xmax[1] ] - return input_item_copy, label_item_copy, weight_item + return input_item, label_item, weight_item class SqueezeData: - """Squeeze data class. + """Squeeze data clsss. Args: apply_keys (Tuple[str, ...], optional): Which data is the squeeze method applied to. Defaults to ("input", "label"). @@ -204,28 +199,27 @@ def __init__(self, apply_keys: Tuple[str, ...] = ("input", "label")): ) self.apply_keys = apply_keys - def __call__(self, input_item, label_item, weight_item): - input_item_copy = {**input_item} - label_item_copy = {**label_item} + def __call__(self, data): + input_item, label_item, weight_item = data if "input" in self.apply_keys: - for key, value in input_item_copy.items(): + for key, value in input_item.items(): if value.ndim == 4: B, C, H, W = value.shape - input_item_copy[key] = value.reshape((B * C, H, W)) + input_item[key] = value.reshape((B * C, H, W)) if value.ndim != 3: raise ValueError( f"Only support squeeze data to ndim=3 now, but got ndim={value.ndim}" ) if "label" in self.apply_keys: - for key, value in label_item_copy.items(): + for key, value in label_item.items(): if value.ndim == 4: B, C, H, W = value.shape - label_item_copy[key] = value.reshape((B * C, H, W)) + label_item[key] = value.reshape((B * C, H, W)) if value.ndim != 3: raise ValueError( f"Only support squeeze data to ndim=3 now, but got ndim={value.ndim}" ) - return input_item_copy, label_item_copy, weight_item + return input_item, label_item, weight_item class FunctionalTransform: @@ -237,11 +231,11 @@ class FunctionalTransform: Examples: >>> import ppsci >>> import numpy as np - >>> def transform_func(data_dict, label_dict, weight_dict): + >>> def transform_func(data_dict): ... rand_ratio = np.random.rand() ... for key in data_dict: ... data_dict[key] = data_dict[key] * rand_ratio - ... return data_dict, label_dict, weight_dict + ... return data_dict >>> transform_cfg = { ... "transforms": ( ... { @@ -259,11 +253,5 @@ def __init__( ): self.transform_func = transform_func - def __call__( - self, *data: Tuple[Dict[str, np.ndarray], ...] - ) -> Tuple[Dict[str, np.ndarray], ...]: - data_dict, label_dict, weight_dict = data - data_dict_copy = {**data_dict} - label_dict_copy = {**label_dict} - weight_dict_copy = {**weight_dict} if weight_dict is not None else {} - return self.transform_func(data_dict_copy, label_dict_copy, weight_dict_copy) + def __call__(self, data_dict: Dict[str, np.ndarray]): + return self.transform_func(data_dict) diff --git a/ppsci/equation/pde/base.py b/ppsci/equation/pde/base.py index 27444a493..a9cfa599a 100644 --- a/ppsci/equation/pde/base.py +++ b/ppsci/equation/pde/base.py @@ -19,7 +19,6 @@ from typing import List from typing import Optional from typing import Tuple -from typing import Union import paddle import sympy @@ -39,16 +38,14 @@ def __init__(self): self.detach_keys: Optional[Tuple[str, ...]] = None - def create_symbols( - self, symbol_str: str - ) -> Union[sympy.Symbol, Tuple[sympy.Symbol, ...]]: + def create_symbols(self, symbol_str: str) -> Tuple[sympy.Symbol, ...]: """Create symbols Args: symbol_str (str): String contains symbols, such as "x", "x y z". Returns: - Union[sympy.Symbol, Tuple[sympy.Symbol, ...]]: Created symbol(s). + Tuple[sympy.Symbol, ...]: Created symbol(s). """ return sympy.symbols(symbol_str) diff --git a/ppsci/equation/pde/navier_stokes.py b/ppsci/equation/pde/navier_stokes.py index 41cb819bf..041d035c2 100644 --- a/ppsci/equation/pde/navier_stokes.py +++ b/ppsci/equation/pde/navier_stokes.py @@ -58,7 +58,7 @@ class NavierStokes(base.PDE): nu (Union[float, str]): Dynamic viscosity. rho (Union[float, str]): Density. dim (int): Dimension of equation. - time (bool): Whether the equation is time-dependent. + time (bool): Whether the euqation is time-dependent. detach_keys (Optional[Tuple[str, ...]]): Keys used for detach during computing. Defaults to None. diff --git a/ppsci/geometry/csg.py b/ppsci/geometry/csg.py index 87534bedd..c09a4b468 100644 --- a/ppsci/geometry/csg.py +++ b/ppsci/geometry/csg.py @@ -128,7 +128,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: value, the shape is [N, D]. Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. """ sdf1 = self.geom1.sdf_func(points) sdf2 = self.geom2.sdf_func(points) @@ -222,7 +222,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: value, the shape is [N, D]. Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. """ sdf1 = self.geom1.sdf_func(points) sdf2 = self.geom2.sdf_func(points) @@ -330,7 +330,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: value the shape is [N, D]. Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. """ sdf1 = self.geom1.sdf_func(points) sdf2 = self.geom2.sdf_func(points) diff --git a/ppsci/geometry/geometry.py b/ppsci/geometry/geometry.py index 2b2709955..ee5be07fa 100644 --- a/ppsci/geometry/geometry.py +++ b/ppsci/geometry/geometry.py @@ -58,7 +58,7 @@ def boundary_normal(self, x): raise NotImplementedError(f"{self}.boundary_normal is not implemented") def uniform_points(self, n: int, boundary=True): - """Compute the equi-spaced points in the geometry.""" + """Compute the equispaced points in the geometry.""" logger.warning( f"{self}.uniform_points not implemented. " f"Use random_points instead." ) @@ -100,25 +100,25 @@ def sample_interior( if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample interior points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) # if sdf_func added, return x_dict and sdf_dict, else, only return the x_dict if hasattr(self, "sdf_func"): sdf = -self.sdf_func(x) sdf_dict = misc.convert_to_dict(sdf, ("sdf",)) - sdf_derives_dict = {} + sdf_derivs_dict = {} if compute_sdf_derivatives: - sdf_derives = -self.sdf_derivatives(x) - sdf_derives_dict = misc.convert_to_dict( - sdf_derives, tuple(f"sdf__{key}" for key in self.dim_keys) + sdf_derivs = -self.sdf_derivatives(x) + sdf_derivs_dict = misc.convert_to_dict( + sdf_derivs, tuple(f"sdf__{key}" for key in self.dim_keys) ) else: sdf_dict = {} - sdf_derives_dict = {} + sdf_derivs_dict = {} x_dict = misc.convert_to_dict(x, self.dim_keys) - return {**x_dict, **sdf_dict, **sdf_derives_dict} + return {**x_dict, **sdf_dict, **sdf_derivs_dict} def sample_boundary(self, n, random="pseudo", criteria=None, evenly=False): """Compute the random points in the geometry and return those meet criteria.""" @@ -189,7 +189,7 @@ def random_points(self, n: int, random: str = "pseudo"): """Compute the random points in the geometry.""" def uniform_boundary_points(self, n: int): - """Compute the equi-spaced points on the boundary.""" + """Compute the equispaced points on the boundary.""" logger.warning( f"{self}.uniform_boundary_points not implemented. " f"Use random_boundary_points instead." @@ -223,13 +223,13 @@ def sdf_derivatives(self, x: np.ndarray, epsilon: float = 1e-4) -> np.ndarray: "when using 'sdf_derivatives'." ) # Only compute sdf derivatives for those already implement `sdf_func` method. - sdf_derives = np.empty_like(x) + sdf_derivs = np.empty_like(x) for i in range(self.ndim): h = np.zeros_like(x) h[:, i] += epsilon / 2 - derives_at_i = (self.sdf_func(x + h) - self.sdf_func(x - h)) / epsilon - sdf_derives[:, i : i + 1] = derives_at_i - return sdf_derives + derivs_at_i = (self.sdf_func(x + h) - self.sdf_func(x - h)) / epsilon + sdf_derivs[:, i : i + 1] = derivs_at_i + return sdf_derivs def union(self, other): """CSG Union.""" diff --git a/ppsci/geometry/geometry_1d.py b/ppsci/geometry/geometry_1d.py index d5de01fe5..ed5c30f2b 100644 --- a/ppsci/geometry/geometry_1d.py +++ b/ppsci/geometry/geometry_1d.py @@ -104,7 +104,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape is [N, 1] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside diff --git a/ppsci/geometry/geometry_2d.py b/ppsci/geometry/geometry_2d.py index a984c6429..d56ed7b20 100644 --- a/ppsci/geometry/geometry_2d.py +++ b/ppsci/geometry/geometry_2d.py @@ -88,7 +88,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape is [N, 2] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside @@ -211,7 +211,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape of the array is [N, 2]. Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside @@ -412,7 +412,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape of the array is [N, 2]. Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside @@ -457,7 +457,7 @@ class Polygon(geometry.Geometry): Args: vertices (Tuple[Tuple[float, float], ...]): The order of vertices can be in a - clockwise or counter-clockwise direction. The vertices will be re-ordered in + clockwise or counterclockwisedirection. The vertices will be re-ordered in counterclockwise (right hand rule). Examples: @@ -611,7 +611,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: points (np.ndarray): The coordinate points used to calculate the SDF value, the shape is [N, 2] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside the object(interior points) is negative, the outside is positive, and the edge diff --git a/ppsci/geometry/geometry_3d.py b/ppsci/geometry/geometry_3d.py index 8af958b1b..7089b9896 100644 --- a/ppsci/geometry/geometry_3d.py +++ b/ppsci/geometry/geometry_3d.py @@ -140,7 +140,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape is [N, 3] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside @@ -186,7 +186,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape is [N, 3] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside diff --git a/ppsci/geometry/geometry_nd.py b/ppsci/geometry/geometry_nd.py index 84a8a3edb..7b1b988f3 100644 --- a/ppsci/geometry/geometry_nd.py +++ b/ppsci/geometry/geometry_nd.py @@ -76,6 +76,10 @@ def boundary_normal(self, x): # For vertices, the normal is averaged for all directions idx = np.count_nonzero(_n, axis=-1) > 1 if np.any(idx): + print( + f"Warning: {self.__class__.__name__} boundary_normal called on vertices. " + "You may use PDE(..., exclusions=...) to exclude the vertices." + ) l = np.linalg.norm(_n[idx], axis=-1, keepdims=True) _n[idx] /= l return _n diff --git a/ppsci/geometry/mesh.py b/ppsci/geometry/mesh.py index 2e03ffb54..cd30668a9 100644 --- a/ppsci/geometry/mesh.py +++ b/ppsci/geometry/mesh.py @@ -18,7 +18,6 @@ from typing import Callable from typing import Dict from typing import Optional -from typing import Tuple from typing import Union import numpy as np @@ -59,35 +58,10 @@ def __init__(self, mesh: Union["pymesh.Mesh", str]): elif isinstance(mesh, pymesh.Mesh): self.py_mesh = mesh else: - raise ValueError("arg `mesh` should be path string or `pymesh.Mesh`") + raise ValueError("arg `mesh` should be path string or or `pymesh.Mesh`") self.init_mesh() - @classmethod - def from_pymesh(cls, mesh: "pymesh.Mesh") -> "Mesh": - """Instantiate Mesh object with given PyMesh object. - - Args: - mesh (pymesh.Mesh): PyMesh object. - - Returns: - Mesh: Instantiated ppsci.geometry.Mesh object. - """ - # check if pymesh is installed when using Mesh Class - if not checker.dynamic_import_to_globals(["pymesh"]): - raise ImportError( - "Could not import pymesh python package." - "Please install it as https://pymesh.readthedocs.io/en/latest/installation.html." - ) - import pymesh - - if isinstance(mesh, pymesh.Mesh): - return cls(mesh) - else: - raise ValueError( - f"arg `mesh` should be type of `pymesh.Mesh`, but got {type(mesh)}" - ) - def init_mesh(self): """Initialize necessary variables for mesh""" if "face_normal" not in self.py_mesh.get_attribute_names(): @@ -143,7 +117,7 @@ def sdf_func(self, points: np.ndarray) -> np.ndarray: the shape is [N, 3] Returns: - np.ndarray: SDF values of input points without squared, the shape is [N, 1]. + np.ndarray: Unsquared SDF values of input points, the shape is [N, 1]. NOTE: This function usually returns ndarray with negative values, because according to the definition of SDF, the SDF value of the coordinate point inside @@ -169,20 +143,7 @@ def is_inside(self, x): def on_boundary(self, x): return np.isclose(self.sdf_func(x), 0.0).flatten() - def translate(self, translation: np.ndarray, relative: bool = True) -> "Mesh": - """Translate by given offsets. - - NOTE: This API generate a completely new Mesh object with translated geometry, - without modifying original Mesh object inplace. - - Args: - translation (np.ndarray): Translation offsets, numpy array of shape (3,): - [offset_x, offset_y, offset_z]. - relative (bool, optional): Whether translate relatively. Defaults to True. - - Returns: - Mesh: Translated Mesh object. - """ + def translate(self, translation, relative=True): vertices = np.array(self.vertices, dtype=paddle.get_default_dtype()) faces = np.array(self.faces) @@ -200,26 +161,13 @@ def translate(self, translation: np.ndarray, relative: bool = True) -> "Mesh": open3d.utility.Vector3iVector(faces), ) open3d_mesh = open3d_mesh.translate(translation, relative) - translated_mesh = pymesh.form_mesh( + self.py_mesh = pymesh.form_mesh( np.asarray(open3d_mesh.vertices, dtype=paddle.get_default_dtype()), faces ) - # Generate a new Mesh object using class method - return Mesh.from_pymesh(translated_mesh) - - def scale(self, scale: float, center: Tuple[float, float, float] = (0, 0, 0)): - """Scale by given scale coefficient and center coordinate. - - NOTE: This API generate a completely new Mesh object with scaled geometry, - without modifying original Mesh object inplace. - - Args: - scale (float): Scale coefficient. - center (Tuple[float,float,float], optional): Center coordinate, [x, y, z]. - Defaults to (0, 0, 0). + self.init_mesh() + return self - Returns: - Mesh: Scaled Mesh object. - """ + def scale(self, scale, center=(0, 0, 0)): vertices = np.array(self.vertices, dtype=paddle.get_default_dtype()) faces = np.array(self.faces, dtype=paddle.get_default_dtype()) @@ -237,14 +185,14 @@ def scale(self, scale: float, center: Tuple[float, float, float] = (0, 0, 0)): open3d.utility.Vector3iVector(faces), ) open3d_mesh = open3d_mesh.scale(scale, center) - scaled_pymesh = pymesh.form_mesh( + self.py_mesh = pymesh.form_mesh( np.asarray(open3d_mesh.vertices, dtype=paddle.get_default_dtype()), faces ) - # Generate a new Mesh object using class method - return Mesh.from_pymesh(scaled_pymesh) + self.init_mesh() + return self def uniform_boundary_points(self, n: int): - """Compute the equi-spaced points on the boundary.""" + """Compute the equispaced points on the boundary.""" return self.pysdf.sample_surface(n) def inflated_random_points(self, n, distance, random="pseudo", criteria=None): @@ -393,7 +341,7 @@ def sample_boundary( evenly, inflation_dist=None, ) - for key, value in data_dict.items(): + for key, value in data_dict: if key not in inflated_data_dict: inflated_data_dict[key] = value else: @@ -433,7 +381,7 @@ def sample_boundary( if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample boundary points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) all_points = np.concatenate(all_points, axis=0) @@ -499,18 +447,18 @@ def sample_interior( x_dict = misc.convert_to_dict(points, self.dim_keys) area_dict = misc.convert_to_dict(areas, ("area",)) - # NOTE: add negative to the sdf values because weight should be positive. + # NOTE: add negtive to the sdf values because weight should be positive. sdf = -self.sdf_func(points) sdf_dict = misc.convert_to_dict(sdf, ("sdf",)) - sdf_derives_dict = {} + sdf_derivs_dict = {} if compute_sdf_derivatives: - sdf_derives = -self.sdf_derivatives(points) - sdf_derives_dict = misc.convert_to_dict( - sdf_derives, tuple(f"sdf__{key}" for key in self.dim_keys) + sdf_derivs = -self.sdf_derivatives(points) + sdf_derivs_dict = misc.convert_to_dict( + sdf_derivs, tuple(f"sdf__{key}" for key in self.dim_keys) ) - return {**x_dict, **area_dict, **sdf_dict, **sdf_derives_dict} + return {**x_dict, **area_dict, **sdf_dict, **sdf_derivs_dict} def union(self, other: "Mesh"): if not checker.dynamic_import_to_globals(["pymesh"]): diff --git a/ppsci/geometry/pointcloud.py b/ppsci/geometry/pointcloud.py index cad7667a6..adedd847b 100644 --- a/ppsci/geometry/pointcloud.py +++ b/ppsci/geometry/pointcloud.py @@ -119,7 +119,7 @@ def scale(self, scale): return self def uniform_boundary_points(self, n: int): - """Compute the equi-spaced points on the boundary.""" + """Compute the equispaced points on the boundary.""" raise NotImplementedError( "PointCloud do not have 'uniform_boundary_points' method" ) @@ -147,7 +147,7 @@ def random_points(self, n, random="pseudo"): ] def uniform_points(self, n: int, boundary=True): - """Compute the equi-spaced points in the geometry.""" + """Compute the equispaced points in the geometry.""" return self.interior[:n] def union(self, other): diff --git a/ppsci/geometry/sampler.py b/ppsci/geometry/sampler.py index 3960bf29c..6190bd923 100644 --- a/ppsci/geometry/sampler.py +++ b/ppsci/geometry/sampler.py @@ -27,7 +27,7 @@ def sample( n_samples: int, ndim: int, method: Literal["pseudo", "LHS"] = "pseudo" ) -> np.ndarray: - """Generate pseudorandom or quasi-random samples in [0, 1]^ndim. + """Generate pseudorandom or quasirandom samples in [0, 1]^ndim. Args: n_samples (int): The number of samples. diff --git a/ppsci/geometry/timedomain.py b/ppsci/geometry/timedomain.py index 740a1a71b..8d9d51141 100644 --- a/ppsci/geometry/timedomain.py +++ b/ppsci/geometry/timedomain.py @@ -111,7 +111,7 @@ def boundary_normal(self, x): return np.hstack((x[:, :1], normal)) def uniform_points(self, n, boundary=True): - """Uniform points on the spatial-temporal domain. + """Uniform points on the spatio-temporal domain. Geometry volume ~ bbox. Time volume ~ diam. @@ -246,7 +246,7 @@ def random_points(self, n, random="pseudo", criteria=None): if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample interior points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) tx = [] @@ -288,7 +288,7 @@ def random_points(self, n, random="pseudo", criteria=None): return np.hstack((t, x)) def uniform_boundary_points(self, n, criteria=None): - """Uniform boundary points on the spatial-temporal domain. + """Uniform boundary points on the spatio-temporal domain. Geometry surface area ~ bbox. Time surface area ~ diam. @@ -329,7 +329,7 @@ def uniform_boundary_points(self, n, criteria=None): if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample boundary points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) nx = len(x) @@ -390,7 +390,7 @@ def random_boundary_points(self, n, random="pseudo", criteria=None): if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample boundary points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) t_x = [] @@ -464,7 +464,7 @@ def random_boundary_points(self, n, random="pseudo", criteria=None): if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample boundary points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) t_x = [] @@ -573,27 +573,27 @@ def sample_initial_interior( if _ntry >= 1000 and _nsuc == 0: raise ValueError( "Sample initial interior points failed, " - "please check correctness of geometry and given criteria." + "please check correctness of geometry and given creteria." ) # if sdf_func added, return x_dict and sdf_dict, else, only return the x_dict if hasattr(self.geometry, "sdf_func"): - # compute sdf excluding time t + # compute sdf excluding timet t sdf = -self.geometry.sdf_func(x[..., 1:]) sdf_dict = misc.convert_to_dict(sdf, ("sdf",)) - sdf_derives_dict = {} + sdf_derivs_dict = {} if compute_sdf_derivatives: - # compute sdf derivatives excluding time t - sdf_derives = -self.geometry.sdf_derivatives(x[..., 1:]) - sdf_derives_dict = misc.convert_to_dict( - sdf_derives, tuple(f"sdf__{key}" for key in self.geometry.dim_keys) + # compute sdf derivatives excluding timet t + sdf_derivs = -self.geometry.sdf_derivatives(x[..., 1:]) + sdf_derivs_dict = misc.convert_to_dict( + sdf_derivs, tuple(f"sdf__{key}" for key in self.geometry.dim_keys) ) else: sdf_dict = {} - sdf_derives_dict = {} + sdf_derivs_dict = {} x_dict = misc.convert_to_dict(x, self.dim_keys) - return {**x_dict, **sdf_dict, **sdf_derives_dict} + return {**x_dict, **sdf_dict, **sdf_derivs_dict} def __str__(self) -> str: """Return the name of class""" diff --git a/ppsci/loss/mtl/agda.py b/ppsci/loss/mtl/agda.py index 5ce66101d..997dc83a5 100644 --- a/ppsci/loss/mtl/agda.py +++ b/ppsci/loss/mtl/agda.py @@ -55,8 +55,8 @@ def __init__(self, model: nn.Layer, M: int = 100, gamma: float = 0.999) -> None: self.gamma = gamma self.Lf_smooth = 0 self.Lu_smooth = 0 - self.Lf_tilde_acc = 0.0 - self.Lu_tilde_acc = 0.0 + self.Lf_tilde_acc = 0 + self.Lu_tilde_acc = 0 def __call__(self, losses, step: int = 0): if len(losses) != 2: @@ -133,7 +133,7 @@ def _refine_grads(self, grads_list: List[paddle.Tensor]) -> List[paddle.Tensor]: gu_bar = gu_bar - (dot_product / (gf_bar * gf_bar).sum()) * gf_bar grads_list = [gf_bar, gu_bar] - proj_grads: List[paddle.Tensor] = [] + proj_grads = [] for j in range(len(self.losses)): start_idx = 0 for idx, var in enumerate(self.model.parameters()): diff --git a/ppsci/loss/mtl/pcgrad.py b/ppsci/loss/mtl/pcgrad.py index fad64aab7..ab79de219 100644 --- a/ppsci/loss/mtl/pcgrad.py +++ b/ppsci/loss/mtl/pcgrad.py @@ -95,7 +95,7 @@ def proj_grad(grad: paddle.Tensor): grads_list = [proj_grad(grad) for grad in grads_list] # Unpack flattened projected gradients back to their original shapes. - proj_grads: List[paddle.Tensor] = [] + proj_grads = [] for j in range(self.loss_num): start_idx = 0 for idx, var in enumerate(self.model.parameters()): diff --git a/ppsci/metric/l2_rel.py b/ppsci/metric/l2_rel.py index 4de9c186d..5fd6ff45a 100644 --- a/ppsci/metric/l2_rel.py +++ b/ppsci/metric/l2_rel.py @@ -26,7 +26,7 @@ class L2Rel(base.Metric): NOTE: This metric API is slightly different from `MeanL2Rel`, difference is as below: - `L2Rel` regards the input sample as a whole and calculates the l2 relative error of the whole; - - `MeanL2Rel` will calculate L2Rel separately for each input sample and return the average of l2 relative error for all samples. + - `MeanL2Rel` will calculate L2Rel separately for each input sample and return the average of l2 relarive error for all samples. $$ metric = \dfrac{\Vert \mathbf{x} - \mathbf{y} \Vert_2}{\max(\Vert \mathbf{y} \Vert_2, \epsilon)} @@ -70,7 +70,7 @@ class MeanL2Rel(base.Metric): NOTE: This metric API is slightly different from `L2Rel`, difference is as below: - - `MeanL2Rel` will calculate L2Rel separately for each input sample and return the average of l2 relative error for all samples. + - `MeanL2Rel` will calculate L2Rel separately for each input sample and return the average of l2 relarive error for all samples. - `L2Rel` regards the input sample as a whole and calculates the l2 relative error of the whole; $$ diff --git a/ppsci/optimizer/lr_scheduler.py b/ppsci/optimizer/lr_scheduler.py index 4c7cc44fe..70100b160 100644 --- a/ppsci/optimizer/lr_scheduler.py +++ b/ppsci/optimizer/lr_scheduler.py @@ -85,7 +85,7 @@ def __init__( self.verbose = verbose @abc.abstractmethod - def __call__(self, *args, **kwargs) -> lr.LRScheduler: + def __call__(self, *kargs, **kwargs) -> lr.LRScheduler: """Generate an learning rate scheduler. Returns: @@ -150,7 +150,7 @@ class Linear(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.Linear(10, 2, 0.001)() + >>> lr = ppsci.optimizer.lr_scheduler.Linear(10, 2, 0.001) """ def __init__( @@ -218,7 +218,7 @@ class ExponentialDecay(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.ExponentialDecay(10, 2, 1e-3, 0.95, 3)() + >>> lr = ppsci.optimizer.lr_scheduler.ExponentialDecay(10, 2, 1e-3, 0.95, 3) """ def __init__( @@ -280,7 +280,7 @@ class Cosine(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.Cosine(10, 2, 1e-3)() + >>> lr = ppsci.optimizer.lr_scheduler.Cosine(10, 2, 1e-3) """ def __init__( @@ -345,7 +345,7 @@ class Step(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.Step(10, 1, 1e-3, 2, 0.95)() + >>> lr = ppsci.optimizer.lr_scheduler.Step(10, 1, 1e-3, 2, 0.95) """ def __init__( @@ -407,9 +407,7 @@ class Piecewise(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.Piecewise( - ... 10, 1, [2, 4], (1e-3, 1e-4, 1e-5) - ... )() + >>> lr = ppsci.optimizer.lr_scheduler.Piecewise(10, 1, [2, 4], (1e-3, 1e-4)) """ def __init__( @@ -469,7 +467,7 @@ class MultiStepDecay(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.MultiStepDecay(10, 1, 1e-3, (4, 5))() + >>> lr = ppsci.optimizer.lr_scheduler.MultiStepDecay(10, 1, 1e-3, (4, 5)) """ def __init__( @@ -603,7 +601,7 @@ class CosineWarmRestarts(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.CosineWarmRestarts(20, 1, 1e-3, 14, 2)() + >>> lr = ppsci.optimizer.lr_scheduler.CosineWarmRestarts(20, 1, 1e-3, 14, 2) """ def __init__( @@ -658,9 +656,9 @@ class OneCycleLR(LRBase): It has been proposed in [Super-Convergence: Very Fast Training of Neural Networks Using Large Learning Rates](https://arxiv.org/abs/1708.07120). - Please note that the default behavior of this scheduler follows the fastai implementation of one cycle, + Please note that the default behaviour of this scheduler follows the fastai implementation of one cycle, which claims that **"unpublished work has shown even better results by using only two phases"**. - If you want the behavior of this scheduler to be consistent with the paper, please set `three_phase=True`. + If you want the behaviour of this scheduler to be consistent with the paper, please set `three_phase=True`. Args: epochs (int): Total epoch(s). @@ -678,7 +676,7 @@ class OneCycleLR(LRBase): Examples: >>> import ppsci - >>> lr = ppsci.optimizer.lr_scheduler.OneCycleLR(100, 1, 1e-3)() + >>> lr = ppsci.optimizer.lr_scheduler.OneCycleLR(1e-3, 100) """ def __init__( diff --git a/ppsci/optimizer/optimizer.py b/ppsci/optimizer/optimizer.py index 12151a026..c1a505d6d 100644 --- a/ppsci/optimizer/optimizer.py +++ b/ppsci/optimizer/optimizer.py @@ -45,7 +45,7 @@ class SGD: weight_decay (Optional[Union[float, regularizer.L1Decay, regularizer.L2Decay]]): Regularization strategy. Defaults to None. grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): - Gradient clipping strategy. Defaults to None. + Gradient cliping strategy. Defaults to None. Examples: >>> import ppsci @@ -93,7 +93,7 @@ class Momentum: weight_decay (Optional[Union[float, regularizer.L1Decay, regularizer.L2Decay]]): Regularization strategy. Defaults to None. grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): - Gradient clipping strategy. Defaults to None. + Gradient cliping strategy. Defaults to None. use_nesterov (bool, optional): Whether to use nesterov momentum. Defaults to False. no_weight_decay_name (Optional[str]): List of names of no weight decay parameters split by white space. Defaults to None. @@ -186,7 +186,7 @@ class Adam: beta2 (float, optional): The exponential decay rate for the 2nd moment estimates. Defaults to 0.999. epsilon (float, optional): A small float value for numerical stability. Defaults to 1e-08. weight_decay (Optional[Union[float, regularizer.L1Decay, regularizer.L2Decay]]): Regularization strategy. Defaults to None. - grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): Gradient clipping strategy. Defaults to None. + grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): Gradient cliping strategy. Defaults to None. lazy_mode (bool, optional): Whether to enable lazy mode for moving-average. Defaults to False. Examples: @@ -252,7 +252,7 @@ class LBFGS: tolerance_grad (float, optional): Termination tolerance on first order optimality. Defaults to 1e-07. tolerance_change (float, optional): termination tolerance on function - value/parameter changes. Defaults to 1e-09. + value/parameterchanges. Defaults to 1e-09. history_size (int, optional): Update history size. Defaults to 100. line_search_fn (Optional[Literal["strong_wolfe"]]): Either 'strong_wolfe' or None. Defaults to "strong_wolfe". @@ -325,7 +325,7 @@ class RMSProp: weight_decay (Optional[Union[float, regularizer.L1Decay, regularizer.L2Decay]]): Regularization strategy. Defaults to None. grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): - Gradient clipping strategy. Defaults to None. + Gradient cliping strategy. Defaults to None. Examples: >>> import ppsci @@ -382,8 +382,8 @@ class AdamW: beta1 (float, optional): The exponential decay rate for the 1st moment estimates. Defaults to 0.9. beta2 (float, optional): The exponential decay rate for the 2nd moment estimates. Defaults to 0.999. epsilon (float, optional): A small float value for numerical stability. Defaults to 1e-8. - weight_decay (float, optional): Regularization coefficient. Defaults to 0.01. - grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): Gradient clipping strategy. Defaults to None. + weight_decay (float, optional): Regularization cofficient. Defaults to 0.01. + grad_clip (Optional[Union[nn.ClipGradByNorm, nn.ClipGradByValue, nn.ClipGradByGlobalNorm]]): Gradient cliping strategy. Defaults to None. no_weight_decay_name (Optional[str]): List of names of no weight decay parameters split by white space. Defaults to None. one_dim_param_no_weight_decay (bool, optional): Apply no weight decay on 1-D parameter(s). Defaults to False. diff --git a/ppsci/probability/hmc.py b/ppsci/probability/hmc.py index fa3f5ea82..010b20901 100644 --- a/ppsci/probability/hmc.py +++ b/ppsci/probability/hmc.py @@ -12,8 +12,6 @@ # See the License for the specific language governing permissions and # limitations under the License. -from __future__ import annotations - from typing import Callable from typing import Dict @@ -104,7 +102,7 @@ def sample( def run_chain( self, epochs: int, initial_position: Dict[str, paddle.Tensor] ) -> Dict[str, paddle.Tensor]: - sampling_result: Dict[str, paddle.Tensor] = {} + sampling_result = {} for k in initial_position.keys(): sampling_result[k] = [] pos = initial_position diff --git a/ppsci/solver/eval.py b/ppsci/solver/eval.py index 8948a4b44..95a2832d1 100644 --- a/ppsci/solver/eval.py +++ b/ppsci/solver/eval.py @@ -12,13 +12,10 @@ # See the License for the specific language governing permissions and # limitations under the License. -from __future__ import annotations - import time from typing import TYPE_CHECKING from typing import Dict from typing import Tuple -from typing import Union import paddle from paddle import io @@ -29,41 +26,13 @@ # from ppsci.utils import profiler if TYPE_CHECKING: - from pgl.utils import data as pgl_data - from ppsci import solver -def _get_dataset_length( - data_loader: Union["io.DataLoader", "pgl_data.Dataloader", "io.IterableDataset"] -) -> int: - """Get full dataset length of given dataloader. - - Args: - data_loader (Union[io.DataLoader, pgl_data.Dataloader, io.IterableDataset]): - Given dataloader. - - Returns: - int: Length of full dataset. - """ - if isinstance(data_loader, io.DataLoader): - num_samples = len(data_loader.dataset) - elif isinstance(data_loader, io.IterableDataset): - num_samples = data_loader.num_samples - elif str(type(data_loader)) == "": - num_samples = len(data_loader.dataset) - else: - raise NotImplementedError( - f"Can not fetch the length of given dataset({type(data_loader)})." - ) - - return num_samples - - def _eval_by_dataset( solver: "solver.Solver", epoch_id: int, log_freq: int ) -> Tuple[float, Dict[str, Dict[str, float]]]: - """Evaluate with computing metric on total samples(default process). + """Evaluate with computing metric on total samples. Args: solver (solver.Solver): Main Solver. @@ -74,12 +43,15 @@ def _eval_by_dataset( Tuple[float, Dict[str, Dict[str, float]]]: Target metric and all metric dicts computed during evaluation. """ - target_metric: float = float("inf") + target_metric: float = None for _, _validator in solver.validator.items(): all_input = misc.Prettydefaultdict(list) all_output = misc.Prettydefaultdict(list) all_label = misc.Prettydefaultdict(list) - num_samples = _get_dataset_length(_validator.data_loader) + if isinstance(_validator.data_loader, io.DataLoader): + num_samples = len(_validator.data_loader.dataset) + else: + num_samples = _validator.data_loader.num_samples loss_dict = misc.Prettydefaultdict(float) reader_tic = time.perf_counter() @@ -114,21 +86,19 @@ def _eval_by_dataset( # collect batch data for key, input in input_dict.items(): all_input[key].append( - (input.detach() if hasattr(input, "detach") else input) + input.detach() if solver.world_size == 1 else misc.all_gather(input.detach()) ) - for key, output in output_dict.items(): all_output[key].append( - (output.detach() if hasattr(output, "detach") else output) + output.detach() if solver.world_size == 1 else misc.all_gather(output.detach()) ) - for key, label in label_dict.items(): all_label[key].append( - (label.detach() if hasattr(label, "detach") else label) + label.detach() if solver.world_size == 1 else misc.all_gather(label.detach()) ) @@ -150,31 +120,24 @@ def _eval_by_dataset( reader_tic = time.perf_counter() batch_tic = time.perf_counter() - # concatenate all data and discard padded sample(s) + # concate all data and discard padded sample(s) for key in all_input: - if paddle.is_tensor(all_input[key][0]): - all_input[key] = paddle.concat(all_input[key]) + all_input[key] = paddle.concat(all_input[key]) if len(all_input[key]) > num_samples: all_input[key] = all_input[key][:num_samples] - for key in all_output: - if paddle.is_tensor(all_output[key][0]): - all_output[key] = paddle.concat(all_output[key]) + all_output[key] = paddle.concat(all_output[key]) if len(all_output[key]) > num_samples: all_output[key] = all_output[key][:num_samples] - for key in all_label: - if paddle.is_tensor(all_label[key][0]): - all_label[key] = paddle.concat(all_label[key]) + all_label[key] = paddle.concat(all_label[key]) if len(all_label[key]) > num_samples: all_label[key] = all_label[key][:num_samples] - metric_dict_group: Dict[str, Dict[str, float]] = misc.PrettyOrderedDict() + metric_dict_group = misc.PrettyOrderedDict() for metric_name, metric_func in _validator.metric.items(): metric_dict = metric_func(all_output, all_label) - metric_dict_group[metric_name] = { - k: float(v) for k, v in metric_dict.items() - } + metric_dict_group[metric_name] = metric_dict for var_name, metric_value in metric_dict.items(): metric_str = f"{metric_name}.{var_name}({_validator.name})" if metric_str not in solver.eval_output_info: @@ -186,11 +149,10 @@ def _eval_by_dataset( ) # use the first metric for return value - tmp = metric_dict_group - while isinstance(tmp, dict): - tmp = next(iter(tmp.values())) - # avoid that none of metric is set - if isinstance(tmp, float): + if target_metric is None: + tmp = metric_dict_group + while isinstance(tmp, dict): + tmp = next(iter(tmp.values())) target_metric = float(tmp) return target_metric, metric_dict_group @@ -210,12 +172,15 @@ def _eval_by_batch( Tuple[float, Dict[str, Dict[str, float]]]: Target metric and all metric dicts computed during evaluation. """ - target_metric: float = float("inf") + target_metric: float = None for _, _validator in solver.validator.items(): - num_samples = _get_dataset_length(_validator.data_loader) + if isinstance(_validator.data_loader, io.DataLoader): + num_samples = len(_validator.data_loader.dataset) + else: + num_samples = _validator.data_loader.num_samples loss_dict = misc.Prettydefaultdict(float) - metric_dict_group: Dict[str, Dict[str, float]] = misc.PrettyOrderedDict() + metric_dict_group = misc.PrettyOrderedDict() reader_tic = time.perf_counter() batch_tic = time.perf_counter() for iter_id, batch in enumerate(_validator.data_loader, start=1): @@ -274,7 +239,7 @@ def _eval_by_batch( reader_tic = time.perf_counter() batch_tic = time.perf_counter() - # concatenate all metric and discard metric of padded sample(s) + # concate all metric and discard metric of padded sample(s) for metric_name, metric_dict in metric_dict_group.items(): for var_name, metric_value in metric_dict.items(): metric_value = paddle.concat(metric_value)[:num_samples] @@ -288,11 +253,10 @@ def _eval_by_batch( solver.eval_output_info[metric_str].update(metric_value, num_samples) # use the first metric for return value - tmp = metric_dict_group - while isinstance(tmp, dict): - tmp = next(iter(tmp.values())) - # avoid that none of metric is set - if isinstance(tmp, float): + if target_metric is None: + tmp = metric_dict_group + while isinstance(tmp, dict): + tmp = next(iter(tmp.values())) target_metric = tmp return target_metric, metric_dict_group diff --git a/ppsci/solver/solver.py b/ppsci/solver/solver.py index dfa6f9d22..f23bf79a2 100644 --- a/ppsci/solver/solver.py +++ b/ppsci/solver/solver.py @@ -16,12 +16,12 @@ import contextlib import itertools +import os import sys +from typing import Any from typing import Callable from typing import Dict -from typing import Mapping from typing import Optional -from typing import Tuple from typing import Union import numpy as np @@ -39,6 +39,7 @@ import ppsci from ppsci.loss import mtl +from ppsci.utils import config from ppsci.utils import expression from ppsci.utils import logger from ppsci.utils import misc @@ -125,7 +126,7 @@ def __init__( seed: int = 42, use_vdl: bool = False, use_wandb: bool = False, - wandb_config: Optional[Mapping] = None, + wandb_config: Optional[Dict[str, str]] = None, device: Literal["cpu", "gpu", "xpu"] = "gpu", equation: Optional[Dict[str, ppsci.equation.PDE]] = None, geom: Optional[Dict[str, ppsci.geometry.Geometry]] = None, @@ -167,13 +168,13 @@ def __init__( self.start_eval_epoch = start_eval_epoch self.eval_freq = eval_freq - # initialize training log recorder for loss, time cost, metric, etc. + # initialize traning log recorder for loss, time cost, metric, etc. self.train_output_info: Dict[str, misc.AverageMeter] = {} self.train_time_info = { "batch_cost": misc.AverageMeter("batch_cost", ".5f", postfix="s"), "reader_cost": misc.AverageMeter("reader_cost", ".5f", postfix="s"), } - self.train_loss_info: Dict[str, misc.AverageMeter] = {} + self.train_loss_info = {} # initialize evaluation log recorder for loss, time cost, metric, etc. self.eval_output_info: Dict[str, misc.AverageMeter] = {} @@ -286,8 +287,6 @@ def __init__( # TODO(sensen): support different kind of DistributedStrategy fleet.init(is_collective=True) self.model = fleet.distributed_model(self.model) - self.model.input_keys = self.model._layers.input_keys - self.model.output_keys = self.model._layers.output_keys if self.optimizer is not None: self.optimizer = fleet.distributed_optimizer(self.optimizer) logger.warning( @@ -308,7 +307,7 @@ def __init__( self.forward_helper = expression.ExpressionSolver() - # whether enable static for forward pass, defaults to False + # whether enable static for forward pass, default to Fals jit.enable_to_static(to_static) logger.info(f"Set to_static={to_static} for forward computation.") @@ -322,10 +321,13 @@ def __init__( extra_parameters += list(equation.learnable_parameters) def convert_expr( - container_dict: Union[ - Dict[str, ppsci.constraint.Constraint], - Dict[str, ppsci.validate.Validator], - Dict[str, ppsci.visualize.Visualizer], + container_dict: Dict[ + str, + Union[ + ppsci.constraint.Constraint, + ppsci.validate.Validator, + ppsci.visualize.Visualizer, + ], ] ) -> None: for container in container_dict.values(): @@ -347,6 +349,95 @@ def convert_expr( if self.visualizer: convert_expr(self.visualizer) + @staticmethod + def from_config(cfg: Dict[str, Any]) -> Solver: + """Initialize solver from given config. + + Args: + cfg (Dict[str, Any]): Dict config, e.g. AttrDict parsed from yaml. + + Returns: + Solver: Initialized solver object. + """ + config.print_config(cfg) + # TODO(sensen): sanity check for config + output_dir = cfg["Global"]["output_dir"] + epochs = cfg["Global"]["epochs"] + iters_per_epoch = cfg["Global"]["iters_per_epoch"] + save_freq = cfg["Global"]["save_freq"] + eval_during_train = cfg["Global"]["eval_during_train"] + eval_freq = cfg["Global"]["eval_freq"] + + seed = cfg["Global"].get("seed", 42) + rank = dist.get_rank() + misc.set_random_seed(seed + rank) + + model = ppsci.arch.build_model(cfg["Arch"]) + geom = ppsci.geometry.build_geometry(cfg.get("Geometry", None)) + equation = ppsci.equation.build_equation(cfg.get("Equation", None)) + constraint = ppsci.constraint.build_constraint( + cfg["Global"].get("Constraint", None), + equation, + geom, + ) + optimizer, lr_scheduler = ppsci.optimizer.build_optimizer( + cfg["Global"]["Optimizer"], + model + ([eq for eq in equation.values()] if equation is not None else []), + epochs, + iters_per_epoch, + ) + + vdl_writer = None + if cfg["Global"].get("vdl_writer", False): + vdl_writer_path = os.path.join(output_dir, "vdl") + os.makedirs(vdl_writer_path, exist_ok=True) + vdl_writer = vdl.LogWriter(vdl_writer_path) + + log_freq = cfg["Global"].get("log_freq", 10) + device = cfg["Global"].get("device", "gpu") + validator = ppsci.validate.build_validator( + cfg.get("Validator", None), equation, geom + ) + visualizer = ppsci.visualize.build_visualizer(cfg.get("Visualizer", None)) + use_amp = "AMP" in cfg + amp_level = cfg["AMP"].pop("level", "O1").upper() if use_amp else "O0" + + start_eval_epoch = cfg["Global"].get("start_eval_epoch", 1) + update_freq = cfg["Global"].get("update_freq", 1) + pretrained_model_path = cfg["Global"].get("pretrained_model_path", None) + checkpoint_path = cfg["Global"].get("checkpoint_path", None) + compute_metric_by_batch = cfg["Global"].get("compute_metric_by_batch", False) + eval_with_no_grad = cfg["Global"].get("eval_with_no_grad", False) + + return Solver( + model, + constraint, + output_dir, + optimizer, + lr_scheduler, + epochs, + iters_per_epoch, + update_freq, + save_freq, + log_freq, + eval_during_train, + start_eval_epoch, + eval_freq, + seed, + vdl_writer, + device, + equation, + geom, + validator, + visualizer, + use_amp, + amp_level, + pretrained_model_path, + checkpoint_path, + compute_metric_by_batch, + eval_with_no_grad, + ) + def train(self): """Training.""" self.global_step = self.best_metric["epoch"] * self.iters_per_epoch @@ -368,7 +459,8 @@ def train(self): and epoch_id % self.eval_freq == 0 and epoch_id >= self.start_eval_epoch ): - cur_metric, metric_dict_group = self.eval(epoch_id) + cur_metric = self.eval(epoch_id) + cur_metric, metric_dict = self.eval(epoch_id) if cur_metric < self.best_metric["metric"]: self.best_metric["metric"] = cur_metric self.best_metric["epoch"] = epoch_id @@ -385,10 +477,7 @@ def train(self): f"[Eval][Epoch {epoch_id}]" f"[best metric: {self.best_metric['metric']}]" ) - for metric_dict in metric_dict_group.values(): - logger.scaler( - metric_dict, epoch_id, self.vdl_writer, self.wandb_writer - ) + logger.scaler(metric_dict, epoch_id, self.vdl_writer, self.wandb_writer) # visualize after evaluation if self.visualizer is not None: @@ -426,15 +515,14 @@ def train(self): self.vdl_writer.close() @misc.run_on_eval_mode - def eval(self, epoch_id: int = 0) -> Tuple[float, Dict[str, Dict[str, float]]]: + def eval(self, epoch_id: int = 0) -> float: """Evaluation. Args: epoch_id (int, optional): Epoch id. Defaults to 0. Returns: - Tuple[float, Dict[str, Dict[str, float]]]: A targe metric value(float) and - all metric(s)(dict) of evaluation, used to judge the quality of the model. + float: The value of the evaluation, used to judge the quality of the model. """ # set eval func self.eval_func = ppsci.solver.eval.eval_func @@ -545,7 +633,7 @@ def predict( key: misc.all_gather(value) for key, value in pred_dict.items() } - # rearrange predictions as the same order of input_dict according to inverse + # rearange predictions as the same order of input_dict according to inverse # permutation, then discard predictions of padding data at the end perm = np.arange(num_samples_pad, dtype="int64") perm = np.concatenate( @@ -661,7 +749,7 @@ def plot_loss_history( """ loss_dict = {} for key in self.train_loss_info: - loss_arr = np.asarray(self.train_loss_info[key].history) + loss_arr = np.array(self.train_loss_info[key].history) if by_epoch: loss_arr = np.mean( np.reshape(loss_arr, (-1, self.iters_per_epoch)), diff --git a/ppsci/solver/train.py b/ppsci/solver/train.py index b31363091..a251e668b 100644 --- a/ppsci/solver/train.py +++ b/ppsci/solver/train.py @@ -12,8 +12,6 @@ # See the License for the specific language governing permissions and # limitations under the License. -from __future__ import annotations - import time from typing import TYPE_CHECKING @@ -64,8 +62,7 @@ def train_epoch_func(solver: "solver.Solver", epoch_id: int, log_freq: int): solver.train_time_info[key].reset() reader_cost += time.perf_counter() - reader_tic for v in input_dict.values(): - if hasattr(v, "stop_gradient"): - v.stop_gradient = False + v.stop_gradient = False # gather each constraint's input, label, weight to a list input_dicts.append(input_dict) @@ -166,8 +163,7 @@ def train_LBFGS_epoch_func(solver: "solver.Solver", epoch_id: int, log_freq: int input_dict, label_dict, weight_dict = next(_constraint.data_iter) reader_cost += time.perf_counter() - reader_tic for v in input_dict.values(): - if hasattr(v, "stop_gradient"): - v.stop_gradient = False + v.stop_gradient = False # gather all constraint data into list input_dicts.append(input_dict) diff --git a/ppsci/solver/visu.py b/ppsci/solver/visu.py index f35c82e05..7876ed557 100644 --- a/ppsci/solver/visu.py +++ b/ppsci/solver/visu.py @@ -77,7 +77,7 @@ def visualize_func(solver: "solver.Solver", epoch_id: int): else misc.all_gather(batch_output.detach().astype("float32")) ) - # concatenate all data + # concate all data for key in all_input: all_input[key] = paddle.concat(all_input[key]) for key in all_output: diff --git a/ppsci/utils/__init__.py b/ppsci/utils/__init__.py index 8f34ed12d..e6e327ffe 100644 --- a/ppsci/utils/__init__.py +++ b/ppsci/utils/__init__.py @@ -35,9 +35,6 @@ from ppsci.utils.symbolic import lambdify __all__ = [ - "AttrDict", - "AverageMeter", - "ExpressionSolver", "initializer", "logger", "misc", @@ -51,6 +48,9 @@ "dynamic_import_to_globals", "run_check", "run_check_mesh", + "AttrDict", + "ExpressionSolver", + "AverageMeter", "set_random_seed", "load_checkpoint", "load_pretrain", diff --git a/ppsci/utils/checker.py b/ppsci/utils/checker.py index d3bb80ba2..4e1b68868 100644 --- a/ppsci/utils/checker.py +++ b/ppsci/utils/checker.py @@ -17,7 +17,7 @@ import importlib.util import traceback from typing import Dict -from typing import Sequence +from typing import Tuple from typing import Union import paddle @@ -245,12 +245,12 @@ def run_check_mesh() -> None: def dynamic_import_to_globals( - names: Union[str, Sequence[str]], alias: Dict[str, str] = None + names: Union[str, Tuple[str, ...]], alias: Dict[str, str] = None ) -> bool: """Import module and add it to globals() by given names dynamically. Args: - names (Union[str, Sequence[str]]): Module name or sequence of module names. + names (Union[str, Tuple[str, ...]]): Module name or list of module names. alias (Dict[str, str]): Alias name of module when imported into globals(). Returns: diff --git a/ppsci/utils/config.py b/ppsci/utils/config.py index f6b3faccf..771616ffc 100644 --- a/ppsci/utils/config.py +++ b/ppsci/utils/config.py @@ -68,7 +68,7 @@ def parse_config(cfg_file): def print_dict(d, delimiter=0): """ Recursively visualize a dict and - indenting according by the relationship of keys. + indenting acrrording by the relationship of keys. """ placeholder = "-" * 60 for k, v in d.items(): @@ -114,7 +114,7 @@ def str2num(v): if not isinstance(dl, (list, dict)): raise ValueError(f"{dl} should be a list or a dict") if len(ks) <= 0: - raise ValueError("length of keys should be larger than 0") + raise ValueError("lenght of keys should be larger than 0") if isinstance(dl, list): k = str2num(ks[0]) diff --git a/ppsci/utils/download.py b/ppsci/utils/download.py index 4c4186f53..c7d4b220e 100644 --- a/ppsci/utils/download.py +++ b/ppsci/utils/download.py @@ -191,7 +191,7 @@ def _decompress(fname): # For protecting decompressing interrupted, # decompress to fpath_tmp directory firstly, if decompress - # succeed, move decompress files to fpath and delete + # successed, move decompress files to fpath and delete # fpath_tmp and remove download compress file. if tarfile.is_tarfile(fname): @@ -199,7 +199,7 @@ def _decompress(fname): elif zipfile.is_zipfile(fname): uncompressed_path = _uncompress_file_zip(fname) else: - raise TypeError(f"Unsupported compress file type {fname}") + raise TypeError(f"Unsupport compress file type {fname}") return uncompressed_path diff --git a/ppsci/utils/logger.py b/ppsci/utils/logger.py index 3b5fc6f0d..d6b0171ef 100644 --- a/ppsci/utils/logger.py +++ b/ppsci/utils/logger.py @@ -172,8 +172,17 @@ def error(msg, *args): def scaler( metric_dict: Dict[str, float], step: int, vdl_writer=None, wandb_writer=None ): - """This function will add scaler data to visualdl or wandb for plotting curve(s). - + """ + [vdl_writer] + This function will draw a scalar curve generated by the visualdl. + Usage: Install visualdl: python -m pip install visualdl==2.0.0b4 + and then: + visualdl --logdir ./scalar --host 0.0.0.0 --port 8830 + to preview loss corve in real time. + + [wandb_writer] + This function will draw a scalar curve generated by the wandb. + Usage: Install wandb: python -m pip install wandb. Args: metric_dict (Dict[str, float]): Metrics dict with metric name and value. step (int): The step of the metric. diff --git a/ppsci/utils/misc.py b/ppsci/utils/misc.py index aaa6f78ea..bf4298860 100644 --- a/ppsci/utils/misc.py +++ b/ppsci/utils/misc.py @@ -18,12 +18,9 @@ import functools import os import random -import time -from contextlib import ContextDecorator from typing import Callable from typing import Dict from typing import List -from typing import Sequence from typing import Tuple from typing import Union @@ -32,14 +29,11 @@ from matplotlib import pyplot as plt from paddle import distributed as dist -from ppsci.utils import logger - __all__ = [ + "all_gather", "AverageMeter", "PrettyOrderedDict", "Prettydefaultdict", - "Timer", - "all_gather", "concat_dict_list", "convert_to_array", "convert_to_dict", @@ -117,57 +111,15 @@ def __str__(self): return "".join([str((k, v)) for k, v in self.items()]) -class Timer(ContextDecorator): - """Count time cost for code block within context. - - Args: - name (str, optional): Name of timer discriminate different code block. - Defaults to "Timer". - auto_print (bool, optional): Whether print time cost when exit context. - Defaults to True. - - Examples: - >>> import paddle - >>> from ppsci.utils import misc - >>> with misc.Timer("test1", auto_print=False) as timer: - ... w = sum(range(0, 10)) - >>> print(f"time cost of 'sum(range(0, 10))' is {timer.interval:.2f}") - time cost of 'sum(range(0, 10))' is 0.00 - - >>> @misc.Timer("test2", auto_print=True) - ... def func(): - ... w = sum(range(0, 10)) - >>> func() # doctest: +SKIP - - """ - - interval: float # Time cost for code within Timer context - - def __init__(self, name: str = "Timer", auto_print: bool = True): - super().__init__() - self.name = name - self.auto_print = auto_print - - def __enter__(self): - self.start_time = time.perf_counter() - return self - - def __exit__(self, type, value, traceback): - self.end_time = time.perf_counter() - self.interval = self.end_time - self.start_time - if self.auto_print: - logger.message(f"{self.name}.time_cost = {self.interval:.2f} s") - - def convert_to_dict(array: np.ndarray, keys: Tuple[str, ...]) -> Dict[str, np.ndarray]: """Split given array into single channel array at axis -1 in order of given keys. Args: - array (np.ndarray): Array to be split. + array (np.ndarray): Array to be splited. keys (Tuple[str, ...]):Keys used in split. Returns: - Dict[str, np.ndarray]: Split dict. + Dict[str, np.ndarray]: Splited dict. """ if array.shape[-1] != len(keys): raise ValueError( @@ -191,7 +143,7 @@ def all_gather( Returns: Union[paddle.Tensor, List[paddle.Tensor]]: Gathered Tensors """ - result: List[paddle.Tensor] = [] + result = [] paddle.distributed.all_gather(result, tensor) if concat: return paddle.concat(result, axis) @@ -212,12 +164,12 @@ def convert_to_array(dict_: Dict[str, np.ndarray], keys: Tuple[str, ...]) -> np. def concat_dict_list( - dict_list: Sequence[Dict[str, np.ndarray]] + dict_list: Tuple[Dict[str, np.ndarray], ...] ) -> Dict[str, np.ndarray]: """Concatenate arrays in tuple of dicts at axis 0. Args: - dict_list (Sequence[Dict[str, np.ndarray]]): Sequence of dicts. + dict_list (Tuple[Dict[str, np.ndarray], ...]): Tuple of dicts. Returns: Dict[str, np.ndarray]: A dict with concatenated arrays for each key. @@ -229,12 +181,12 @@ def concat_dict_list( def stack_dict_list( - dict_list: Sequence[Dict[str, np.ndarray]] + dict_list: Tuple[Dict[str, np.ndarray], ...] ) -> Dict[str, np.ndarray]: """Stack arrays in tuple of dicts at axis 0. Args: - dict_list (Sequence[Dict[str, np.ndarray]]): Sequence of dicts. + dict_list (Tuple[Dict[str, np.ndarray], ...]): Tuple of dicts. Returns: Dict[str, np.ndarray]: A dict with stacked arrays for each key. @@ -261,14 +213,14 @@ def combine_array_with_time(x: np.ndarray, t: Tuple[int, ...]) -> np.ndarray: """Combine given data x with time sequence t. Given x with shape (N, D) and t with shape (T, ), this function will repeat t_i for N times and will concat it with data x for each t_i in t, - finally return the stacked result, which is of shape (N×T, D+1). + finally return the stacked result, which is of shape (NxT, D+1). Args: x (np.ndarray): Points data with shape (N, D). t (Tuple[int, ...]): Time sequence with shape (T, ). Returns: - np.ndarray: Combined data with shape of (N×T, D+1). + np.ndarray: Combined data with shape of (NxT, D+1). """ nx = len(x) tx = [] @@ -284,17 +236,13 @@ def combine_array_with_time(x: np.ndarray, t: Tuple[int, ...]) -> np.ndarray: def cartesian_product(*arrays: np.ndarray) -> np.ndarray: """Cartesian product for input sequence of array(s). - Reference: https://stackoverflow.com/questions/11144513/cartesian-product-of-x-and-y-array-points-into-single-array-of-2d-points - Assume shapes of input arrays are: $(N_1,), (N_2,), (N_3,), ..., (N_M,)$, - then the cartesian product result will be shape of $(N_1×N_2×N_3×...×N_M, M)$. - - Args: - arrays (np.ndarray): Input arrays. + Assume input arrays shape are: (N_1,), (N_2,), (N_3,), ..., (N_M,), + then the cartesian product result will be shape of (N_1*N_2*N_3*...*N_M, M). Returns: - np.ndarray: Cartesian product result of shape $(N_1×N_2×N_3×...×N_M, M)$. + np.ndarray: Cartesian product result of shape (N_1*N_2*N_3*...*N_M, M). Examples: >>> t = np.array([1, 2]) @@ -370,7 +318,7 @@ def run_at_rank0(func: Callable) -> Callable: func (Callable): Given function. Returns: - Callable: Wrapped function which will only run at at rank 0, + Callable: Wrappered function which will only run at at rank 0, skipped at other rank. """ diff --git a/ppsci/utils/reader.py b/ppsci/utils/reader.py index f6738dec6..76c8ef299 100644 --- a/ppsci/utils/reader.py +++ b/ppsci/utils/reader.py @@ -16,6 +16,7 @@ import collections import csv +import sys from typing import Dict from typing import Optional from typing import Tuple @@ -25,6 +26,8 @@ import paddle import scipy.io as sio +from ppsci.utils import logger + __all__ = [ "load_csv_file", "load_mat_file", @@ -38,7 +41,7 @@ def load_csv_file( file_path: str, keys: Tuple[str, ...], alias_dict: Optional[Dict[str, str]] = None, - delimiter: str = ",", + delimeter: str = ",", encoding: str = "utf-8", ) -> Dict[str, np.ndarray]: """Load *.csv file and fetch data as given keys. @@ -59,13 +62,14 @@ def load_csv_file( try: # read all data from csv file with open(file_path, "r", encoding=encoding) as csv_file: - reader = csv.DictReader(csv_file, delimiter=delimiter) + reader = csv.DictReader(csv_file, delimiter=delimeter) raw_data = collections.defaultdict(list) for _, line_dict in enumerate(reader): for key, value in line_dict.items(): raw_data[key].append(value) - except FileNotFoundError as e: - raise e + except FileNotFoundError: + logger.error(f"{file_path} isn't a valid csv file.") + sys.exit() # convert to numpy array data_dict = {} @@ -101,8 +105,9 @@ def load_mat_file( try: # read all data from mat file raw_data = sio.loadmat(file_path) - except FileNotFoundError as e: - raise e + except FileNotFoundError: + logger.error(f"{file_path} isn't a valid mat file.") + raise # convert to numpy array data_dict = {} @@ -138,8 +143,9 @@ def load_npz_file( try: # read all data from npz file raw_data = np.load(file_path, allow_pickle=True) - except FileNotFoundError as e: - raise e + except FileNotFoundError: + logger.error(f"{file_path} isn't a valid npz file.") + raise # convert to numpy array data_dict = {} diff --git a/ppsci/utils/save_load.py b/ppsci/utils/save_load.py index 88480056a..5d6d10182 100644 --- a/ppsci/utils/save_load.py +++ b/ppsci/utils/save_load.py @@ -52,7 +52,7 @@ def _load_pretrain_from_path( ) param_state_dict = paddle.load(f"{path}.pdparams") - model.set_state_dict(param_state_dict) + model.set_dict(param_state_dict) if equation is not None: if not os.path.exists(f"{path}.pdeqn"): logger.warning(f"{path}.pdeqn not found.") @@ -75,11 +75,7 @@ def load_pretrain( equation (Optional[Dict[str, equation.PDE]]): Equations. Defaults to None. """ if path.startswith("http"): - path = download.get_weights_path_from_url(path) - - # remove ".pdparams" in suffix of path for convenient - if path.endswith(".pdparams"): - path = path[:-9] + path = download.get_weights_path_from_url(path).replace(".pdparams", "") _load_pretrain_from_path(path, model, equation) diff --git a/ppsci/utils/symbolic.py b/ppsci/utils/symbolic.py index 84d77ac3e..81e28c6c0 100644 --- a/ppsci/utils/symbolic.py +++ b/ppsci/utils/symbolic.py @@ -74,7 +74,7 @@ sp.Mul, ] -SYMPY_TO_PADDLE = { +SYMPT_TO_PADDLE = { sp.sin: paddle.sin, sp.sinh: paddle.sinh, sp.asin: paddle.asin, @@ -100,7 +100,7 @@ sp.sign: paddle.sign, sp.ceiling: paddle.ceil, sp.floor: paddle.floor, - # NOTE: sp.Add and sp.Mul is not included here for un-alignment with sympy + # NOTE: sp.Add and sp.Mul is not included here for unalignment with sympy # and are implemented manually. } @@ -185,11 +185,11 @@ class OperatorNode(Node): def __init__(self, expr: SYMPY_BUILTIN_FUNC): super().__init__(expr) - # preprocess children's key instead of processing at run-time in forward + # preprocess childs' key instead of processing at run-time in forward # which can reduce considerable overhead of time for calling "_cvt_to_key" if self.expr.func == sp.Derivative: self.childs = [_cvt_to_key(self.expr.args[0])] + [ - (_cvt_to_key(arg), int(order)) for (arg, order) in self.expr.args[1:] + (_cvt_to_key(arg), order) for (arg, order) in self.expr.args[1:] ] else: self.childs = [_cvt_to_key(arg) for arg in self.expr.args] @@ -202,14 +202,14 @@ def __init__(self, expr: SYMPY_BUILTIN_FUNC): self._apply_func = self._derivate_operator_func elif self.expr.func == sp.Heaviside: self._apply_func = self._heaviside_operator_func - self._auxiliary_func = SYMPY_TO_PADDLE[sp.Heaviside] + self._auxiliary_func = SYMPT_TO_PADDLE[sp.Heaviside] elif self.expr.func == sp.Min: self._apply_func = self._minimum_operator_func elif self.expr.func == sp.Max: self._apply_func = self._maximum_operator_func else: self._apply_func = self._vanilla_operator_func - self._auxiliary_func = SYMPY_TO_PADDLE[self.expr.func] + self._auxiliary_func = SYMPT_TO_PADDLE[self.expr.func] def forward(self, data_dict: DATA_DICT): # use cache @@ -369,14 +369,14 @@ def forward(self, data_dict: DATA_DICT) -> DATA_DICT: def _post_traverse(cur_node: sp.Basic, nodes: List[sp.Basic]) -> List[sp.Basic]: - """Traverse sympy expression tree in post-order. + """Traverse sympy expression tree in postorder. Args: cur_node (sp.Basic): Sympy expression of current node. - nodes (List[sp.Basic]): Node list storing all tree nodes in post-order. + nodes (List[sp.Basic]): Node list storing all tree nodes in postorder. Returns: - List[sp.Basic]: Node list storing all tree nodes in post-order. + List[sp.Basic]: Node list storing all tree nodes in postorder. """ # traverse into sub-nodes if isinstance(cur_node, sp.Function): @@ -446,7 +446,7 @@ def get_operator_name(node): graph = pygraphviz.AGraph(directed=True, rankdir="TB") C_FUNC = "#9196f1" # purple color function node - C_DATA = "#feb64d" # orange color for data node + C_DATA = "#feb64d" # oringe color for data node C_EDGE = "#000000" # black color for edge def add_edge(u: str, v: str, u_color: str = C_DATA, v_color: str = C_DATA): @@ -488,13 +488,13 @@ def add_edge(u: str, v: str, u_color: str = C_DATA, v_color: str = C_DATA): graph.draw(image_path, prog="dot") graph.write(dot_path) logger.message( - f"Computational graph has been written to {image_path} and {dot_path}. " + f"Computational graph has been writen to {image_path} and {dot_path}. " "dot file can be visualized at https://dreampuf.github.io/GraphvizOnline/" ) def lambdify( - expr: sp.Basic, + expr: sp.Expr, models: Optional[Union[arch.Arch, Tuple[arch.Arch, ...]]] = None, extra_parameters: Optional[Sequence[paddle.Tensor]] = None, graph_filename: Optional[str] = None, @@ -502,7 +502,7 @@ def lambdify( """Convert sympy expression to callable function. Args: - expr (sp.Basic): Sympy expression to be converted. + expr (sp.Expr): Sympy expression to be converted. models (Optional[Union[arch.Arch, Tuple[arch.Arch, ...]]]): Model(s) for computing forward result in `LayerNode`. extra_parameters (Optional[nn.ParameterList]): Extra learnable parameters. @@ -564,11 +564,11 @@ def lambdify( # remove 1.0 from sympy expression tree expr = expr.subs(1.0, 1) - # convert sympy expression tree to list of nodes in post-order - sympy_nodes: List[sp.Basic] = [] + # convert sympy expression tree to list of nodes in postorder + sympy_nodes = [] sympy_nodes = _post_traverse(expr, sympy_nodes) - # remove unnecessary symbol nodes already in input dict(except for parameter symbol) + # remove unnecessary symbol nodes already in input dict(except for paramter symbol) if not extra_parameters: extra_parameters = () _parameter_names = tuple(param.name for param in extra_parameters) @@ -578,7 +578,7 @@ def lambdify( if (not node.is_Symbol) or (_cvt_to_key(node) in _parameter_names) ] - # remove duplicates with topological order kept + # remove duplicates with topo-order kept sympy_nodes = list(dict.fromkeys(sympy_nodes)) if isinstance(models, arch.ModelList): @@ -590,7 +590,7 @@ def lambdify( callable_nodes = [] for i, node in enumerate(sympy_nodes): if isinstance( - node, tuple(SYMPY_TO_PADDLE.keys()) + (sp.Add, sp.Mul, sp.Derivative) + node, tuple(SYMPT_TO_PADDLE.keys()) + (sp.Add, sp.Mul, sp.Derivative) ): callable_nodes.append(OperatorNode(node)) elif isinstance(node, sp.Function): diff --git a/ppsci/validate/base.py b/ppsci/validate/base.py index 84760f25d..8e7b8959c 100644 --- a/ppsci/validate/base.py +++ b/ppsci/validate/base.py @@ -17,7 +17,6 @@ from typing import TYPE_CHECKING from typing import Any from typing import Dict -from typing import Optional from paddle import io @@ -35,7 +34,7 @@ class Validator: dataset (io.Dataset): Dataset for validator. dataloader_cfg (Dict[str, Any]): Dataloader config. loss (loss.Loss): Loss functor. - metric (Optional[Dict[str, metric.Metric]]): Named metric functors in dict. + metric (Dict[str, metric.Metric]): Named metric functors in dict. name (str): Name of validator. """ @@ -44,7 +43,7 @@ def __init__( dataset: io.Dataset, dataloader_cfg: Dict[str, Any], loss: "loss.Loss", - metric: Optional[Dict[str, "metric.Metric"]], + metric: Dict[str, "metric.Metric"], name: str, ): self.data_loader = data.build_dataloader(dataset, dataloader_cfg) diff --git a/ppsci/validate/sup_validator.py b/ppsci/validate/sup_validator.py index a88a02af5..56f2b9a50 100644 --- a/ppsci/validate/sup_validator.py +++ b/ppsci/validate/sup_validator.py @@ -37,7 +37,7 @@ class SupervisedValidator(base.Validator): Examples: >>> import ppsci - >>> valid_dataloader_cfg = { + >>> valida_dataloader_cfg = { ... "dataset": { ... "name": "MatDataset", ... "file_path": "/path/to/file.mat", @@ -52,7 +52,7 @@ class SupervisedValidator(base.Validator): ... }, ... } # doctest: +SKIP >>> eta_mse_validator = ppsci.validate.SupervisedValidator( - ... valid_dataloader_cfg, + ... valida_dataloader_cfg, ... ppsci.loss.MSELoss("mean"), ... {"eta": lambda out: out["eta"]}, ... metric={"MSE": ppsci.metric.MSE()}, diff --git a/ppsci/visualize/plot.py b/ppsci/visualize/plot.py index 19ebda4bf..e53f0bbe0 100644 --- a/ppsci/visualize/plot.py +++ b/ppsci/visualize/plot.py @@ -80,7 +80,6 @@ def _save_plot_from_1d_array(filename, coord, value, value_keys, num_timestamps= value_keys (Tuple[str, ...]): Value keys. num_timestamps (int, optional): Number of timestamps coord/value contains. Defaults to 1. """ - os.makedirs(os.path.dirname(filename), exist_ok=True) fig, a = plt.subplots(len(value_keys), num_timestamps, squeeze=False) fig.subplots_adjust(hspace=0.8) @@ -174,7 +173,6 @@ def _save_plot_from_2d_array( xticks (Optional[Tuple[float, ...]]): Tuple of xtick locations. Defaults to None. yticks (Optional[Tuple[float, ...]]): Tuple of ytick locations. Defaults to None. """ - os.makedirs(os.path.dirname(filename), exist_ok=True) plt.close("all") matplotlib.rcParams["xtick.labelsize"] = 5 @@ -283,7 +281,7 @@ class HandlerColormap(HandlerBase): Args: cmap (matplotlib.cm): Matplotlib colormap. - num_stripes (int, optional): Number of contour levels (strips) in rectangle. Defaults to 8. + num_stripes (int, optional): Number of countour levels (strips) in rectangle. Defaults to 8. """ def __init__(self, cmap: matplotlib.cm, num_stripes: int = 8, **kw): @@ -321,7 +319,6 @@ def _save_plot_from_3d_array( visu_keys (Tuple[str, ...]): Keys for visualizing data. such as ("u", "v"). num_timestamps (int, optional): Number of timestamps coord/value contains. Defaults to 1. """ - os.makedirs(os.path.dirname(filename), exist_ok=True) fig = plt.figure(figsize=(10, 10)) len_ts = len(visu_data[0]) // num_timestamps @@ -407,12 +404,12 @@ def _save_plot_weather_from_array( pred_key (str): The key of predict data. target_key (str): The key of target data. xticks (Tuple[float, ...]): The list of xtick locations. - xticklabels (Tuple[str, ...]): The x-axis' tick labels. + xticklabels (Tuple[str, ...]): The xaxis' tick labels. yticks (Tuple[float, ...]): The list of ytick locations. - yticklabels (Tuple[str, ...]): The y-axis' tick labels. + yticklabels (Tuple[str, ...]): The yaxis' tick labels. vmin (float): Minimum value that the colormap covers. vmax (float): Maximal value that the colormap covers. - colorbar_label (str, optional): The color-bar label. Defaults to "". + colorbar_label (str, optional): The colorbar label. Defaults to "". log_norm (bool, optional): Whether use log norm. Defaults to False. """ @@ -450,7 +447,6 @@ def plot_weather( ) plt.colorbar(mappable=map_, cax=None, ax=None, shrink=0.5, label=colorbar_label) - os.makedirs(os.path.dirname(filename), exist_ok=True) fig = plt.figure(facecolor="w", figsize=(7, 7)) ax = fig.add_subplot(2, 1, 1) plot_weather( @@ -482,7 +478,7 @@ def plot_weather( def save_plot_weather_from_dict( - foldername: str, + flodername: str, data_dict: Dict[str, Union[np.ndarray, paddle.Tensor]], visu_keys: Tuple[str, ...], xticks: Tuple[float, ...], @@ -498,20 +494,20 @@ def save_plot_weather_from_dict( """Plot weather result as file from dict data. Args: - foldername (str): Output folder name. + flodername (str): Output floder name. data_dict (Dict[str, Union[np.ndarray, paddle.Tensor]]): Data in dict. visu_keys (Tuple[str, ...]): Keys for visualizing data. such as ("output_6h", "target_6h"). xticks (Tuple[float, ...]): The list of xtick locations. - xticklabels (Tuple[str, ...]): The x-axis' tick labels. + xticklabels (Tuple[str, ...]): The xaxis' tick labels. yticks (Tuple[float, ...]): The list of ytick locations, - yticklabels (Tuple[str, ...]): The y-axis' tick labels. + yticklabels (Tuple[str, ...]): The yaxis' tick labels. vmin (float): Minimum value that the colormap covers. vmax (float): Maximal value that the colormap covers. colorbar_label (str, optional): The colorbar label. Defaults to "". log_norm (bool, optional): Whether use log norm. Defaults to False. num_timestamps (int): Number of timestamp in data_dict. Defaults to 1. """ - os.makedirs(foldername, exist_ok=True) + os.makedirs(flodername, exist_ok=True) visu_data = [data_dict[k] for k in visu_keys] if isinstance(visu_data[0], paddle.Tensor): @@ -522,7 +518,7 @@ def save_plot_weather_from_dict( pred_key, target_key = visu_keys[2 * t], visu_keys[2 * t + 1] pred_data = visu_data[2 * t] target_data = visu_data[2 * t + 1] - filename_t = os.path.join(foldername, f"{t}.png") + filename_t = os.path.join(flodername, f"{t}.png") _save_plot_weather_from_array( filename_t, pred_data, @@ -539,7 +535,7 @@ def save_plot_weather_from_dict( log_norm=log_norm, ) frames.append(imageio.imread(filename_t)) - filename = os.path.join(foldername, "result.gif") + filename = os.path.join(flodername, "result.gif") imageio.mimsave( filename, frames, diff --git a/ppsci/visualize/visualizer.py b/ppsci/visualize/visualizer.py index e3e602daa..4a477bc99 100644 --- a/ppsci/visualize/visualizer.py +++ b/ppsci/visualize/visualizer.py @@ -80,9 +80,9 @@ class VisualizerScatter3D(base.Visualizer): Examples: >>> import ppsci - >>> vis_data = {"states": np.random.randn(16, 1)} + >>> vis_datas = {"states": np.random.randn(16, 1)} >>> visualizer = ppsci.visualize.VisualizerScatter3D( - ... vis_data, + ... vis_datas, ... {"states": lambda d: d["states"]}, ... num_timestamps=1, ... prefix="result_states", @@ -216,12 +216,12 @@ class Visualizer2DPlot(Visualizer2D): Examples: >>> import ppsci - >>> vis_data = { + >>> vis_datas = { ... "target_ux": np.random.randn(128, 20, 1), ... "pred_ux": np.random.randn(128, 20, 1), ... } >>> visualizer_states = ppsci.visualize.Visualizer2DPlot( - ... vis_data, + ... vis_datas, ... { ... "target_ux": lambda d: d["states"][:, :, 0], ... "pred_ux": lambda d: output_transform(d)[:, :, 0], @@ -327,12 +327,12 @@ class VisualizerWeather(base.Visualizer): input_dict (Dict[str, np.ndarray]): Input dict. output_expr (Dict[str, Callable]): Output expression. xticks (Tuple[float, ...]): The list of xtick locations. - xticklabels (Tuple[str, ...]): The x-axis' tick labels. + xticklabels (Tuple[str, ...]): The xaxis' tick labels. yticks (Tuple[float, ...]): The list of ytick locations. - yticklabels (Tuple[str, ...]): The y-axis' tick labels. + yticklabels (Tuple[str, ...]): The yaxis' tick labels. vmin (float): Minimum value that the colormap covers. vmax (float): Maximal value that the colormap covers. - colorbar_label (str, optional): The color-bar label. Defaults to "". + colorbar_label (str, optional): The colorbar label. Defaults to "". log_norm (bool, optional): Whether use log norm. Defaults to False. batch_size (int, optional): : Batch size of data when computing result in visu.py. Defaults to 1. num_timestamps (int, optional): Number of timestamps. Defaults to 1. @@ -341,12 +341,12 @@ class VisualizerWeather(base.Visualizer): Examples: >>> import ppsci >>> import numpy as np - >>> vis_data = { + >>> vis_datas = { ... "output_6h": np.random.randn(1, 720, 1440), ... "target_6h": np.random.randn(1, 720, 1440), ... } >>> visualizer_weather = ppsci.visualize.VisualizerWeather( - ... vis_data, + ... vis_datas, ... { ... "output_6h": lambda d: d["output_6h"], ... "target_6h": lambda d: d["target_6h"], diff --git a/ppsci/visualize/vtu.py b/ppsci/visualize/vtu.py index f0d76e987..41ac1659b 100644 --- a/ppsci/visualize/vtu.py +++ b/ppsci/visualize/vtu.py @@ -14,7 +14,6 @@ from __future__ import annotations -import os from typing import Dict from typing import Tuple @@ -53,8 +52,6 @@ def _save_vtu_from_array(filename, coord, value, value_keys, num_timestamps=1): if coord.shape[1] not in [2, 3]: raise ValueError(f"ndim of coord({coord.shape[1]}) should be 2 or 3.") - os.makedirs(os.path.dirname(filename), exist_ok=True) - # discard extension name if filename.endswith(".vtu"): filename = filename[:-4] @@ -152,5 +149,4 @@ def save_vtu_to_mesh( points=points.T, cells=[("vertex", np.arange(npoint).reshape(npoint, 1))] ) mesh.point_data = {key: data_dict[key] for key in value_keys} - os.makedirs(os.path.dirname(filename), exist_ok=True) mesh.write(filename) diff --git a/test/equation/test_navier_stokes.py b/test/equation/test_navier_stokes.py index b2ba2cfb4..0279374ac 100644 --- a/test/equation/test_navier_stokes.py +++ b/test/equation/test_navier_stokes.py @@ -173,9 +173,7 @@ def test_navierstokes(nu, rho, dim, time): # check result whether is equal for name in test_output_names: - assert paddle.allclose( - expected_output[name], test_output[name], atol=1e-7 - ), f"{name}" + assert paddle.allclose(expected_output[name], test_output[name]), f"{name}" if __name__ == "__main__":