- Relationship between Maximum likelihood and distance metrix?
- [solution]:
- 如何理解最小二乘与最大似然估计
- (https://www.zhihu.com/question/20447622)
- 论及本质,其实两者只是用不同的度量空间来进行的投影,OLS的度量是L2 norm distance,而极大似然的度量是Kullback-Leibler divergence.
- 最大似然估计就是去找到那个(组)参数估计值,使得前面已经实现的样本值发生概率最大。因为你手头上的样本已经实现了,其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化,是个连乘积,只要取对数,就变成了线性加总。此时通过对参数求导数,并令一阶导数为零,就可以通过解方程(组),得到最大似然估计值。
- 实例理解
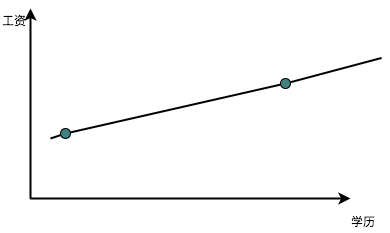
- 最小二乘 设想一个例子,教育程度和工资之间的关系。我们观察到的数据无非就是一个教育程度,对应着一个工资。我们希望的自然是找到两者之间的规律:如果把教育程度的初中、高中、大学、研究生及博士定义为1234的话,我们希望找到类似于工资=1000 +2000x教育程度 的这种规律,其中1000和2000是我们需要从数据里面发现的,前者称之为底薪,后者称之为教育增量薪水。如果我们就观察到两个数据,那解起来很简单,直接把两个数据带进去,二元一次方程组,就得到底薪和教育程度增量薪水之间的关系。这个在图上就体现为两点决定一条直线:
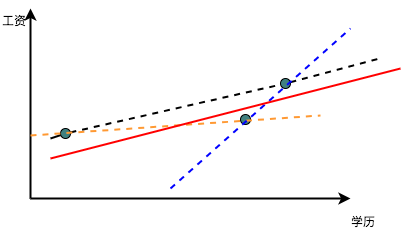
但是如果现在有三个数据,怎么办呢?如果这三个点不在一条线上,我们就需要作出取舍了,如果我们取任意两个点,那么就没有好好的利用第三个点带来的新信息,并且因为这三个点在数据中的地位相同,我们如何来断定应该选用哪两个点来作为我们的基准呢?这就都是问题了。这个时候我们最直观的想法就是『折衷』一下,在这三个数据,三条线中间取得某种平衡作为我们的最终结果,类似于图中的红线这样:
那怎么取平衡呢?那我们现在必须引入误差的存在,也就是我们要承认观测到的数据中有一些因素是不可知的,不能完全的被学历所解释。而这个不能解释的程度,自然就是每个点到红线在Y轴的距离。 但是我们尽管痛苦的承认了有不能解释的因素,但是我们依然想尽可能的让这种『不被解释』的程度最小,于是我们就想最小化这种不被解释的程度。因为点可能在线的上面或者下面,故而距离有正有负,取绝对值又太麻烦,于是我们就直接把每个距离都取一个平方变成正的,然后试图找出一个距离所有点的距离的平方最小的这条线,这就是最小二乘法了,简单粗暴而有效。
- 而极大似然则更加的有哲理一些。还用上面的例子,我们观察到了三个点,于是我们开始反思,为什么我们观察到的是这三个点而不是另外三个?大千世界,芸芸众生,这么多人都有不同的工资,不同的学历,但是偏偏这三个点让我给观察到了。这肯定说明了某种世界的真相。
什么世界的真相呢?因为我们观察到了这三个点,反过来说,冥冥之中注定了这三个点被我们观察到的概率可能是最大的。所以我们希望找到一个特定的底薪和教育增量薪水的组合,让我们观察到这三个点的概率最大,这个找的过程就是极大似然估计。
具体的做法很简单,因为底薪和教育增量薪水虽然我们不知道,但是它一定存在,所以是个固定的值,能够随机变动的就是我们观察不到的神秘误差,那么给定一组底薪和教育增量薪水,必然存在一个唯一的误差与之对应,共同组合成了我们看到的数据。比如说,我们观察到一个人是:
高中毕业(学历变量=2) 工资 4500,如果我们假定工资=1000 +2000x教育程度的话,那么理论上工资应该是5000,而我们观察到了4500,所以这个时候误差为500。而误差=500,根据我们假设的误差的概率函数,总是存在一个概率与之相对应的(这个概率的分布我们可以假设)。而极大似然估计,就是把我们观察到每个样本所对应的误差的概率乘到一起,然后试图调整参数以最大化这个概率的乘积。
其背后的直觉是:假想有一个神秘的超自然力量,他全知全能,自然也知道真实的数据背后的规律。他在你抽样之前先做了一次复杂的计算,把无数个可能的抽样中,最可能出现的那个抽样展示给你。于是你根据这个抽样,逆流而上,倒推出来了数据背后的真实规律。
总结一句话,最小二乘法的核心是权衡,因为你要在很多条线中间选择,选择出距离所有的点之和最短的;而极大似然的核心是自恋,要相信自己是天选之子,自己看到的,就是冥冥之中最接近真相的。
- 最小二乘 设想一个例子,教育程度和工资之间的关系。我们观察到的数据无非就是一个教育程度,对应着一个工资。我们希望的自然是找到两者之间的规律:如果把教育程度的初中、高中、大学、研究生及博士定义为1234的话,我们希望找到类似于工资=1000 +2000x教育程度 的这种规律,其中1000和2000是我们需要从数据里面发现的,前者称之为底薪,后者称之为教育增量薪水。如果我们就观察到两个数据,那解起来很简单,直接把两个数据带进去,二元一次方程组,就得到底薪和教育程度增量薪水之间的关系。这个在图上就体现为两点决定一条直线:
- A和B是两个矩阵,求 tr(A'B),A'指A的转置。(写出来后,我没有检查AB是否size相同,他说应该考虑这种边界条件,并说你考虑了AB是否空矩阵这是比较好的一点)
- 讲一讲SVM,知道多少说多少?为什么要用对偶问题求解?(今日头条)
- 简单讲一下BP是如何计算的?
- SVM加核函数用过吗?讲一讲其中的差别?(今日头条)
- 训练样本多,维度大就可以用核函数;如果样本少,用核函数比较容易过拟合
- SVM在训练的时候有没有遇到hard example?(今日头条)
- SVM对hard example的应用很重要,先用一部分训练集训练一个模型,然后用剩下的一部分训练集的一部分做测试,把出错的再送入重新训练,重复二三次,效果会比较好
- SVM核函数的选择?多项式核和RBF核的关系?
- 说LR和SVM损失函数。
- 推导PCA。具体问很多为什么。为什么是方差最大化?你这个是方差吗?
- XGBoost了解吗
- 讲一下生成模型和判别模型有什么区别
-
你觉得滴滴打车的拼车价是怎么计算出来的,详细描述。(路径规划,订单预测之类的)
-
你觉得滴滴打车的溢价,1.1倍,1.2倍,这些数值是怎么计算出来的?(订单预测,当前司机数量),目的是什么?
-
推导BP神经网络的反向求导。(可以用均方损失函数)