- 定义：树是n个结点的有限集合，在任何一个非空的树中
- 有且只有一个根节点
- 子女：结点的子树非空，结点子树的根即为结点的子女
- 双亲：结点有子女，该结点是子女的双亲
- 兄弟：某一结点的所有子女，互为兄弟
- 度：结点的子女个数
- 分支结点：非终端结点
- 叶：终端结点
- 祖先：沿着双亲的路径返回均为祖先
- 子孙：下属所有结点
- 结点的层次：规定根节点在第一层，子女依次加1
- 深度：层次的最大值
- 树的高度：根节点的高度->所有子女高度+1
- 有序树：树的结点的各棵子树是从左到右有顺序的
- 无序树：无序，各棵子树之间的次序可以呼唤
- 森林：m棵互不相交的树组成
- 二叉树中不存在度大于2的结点
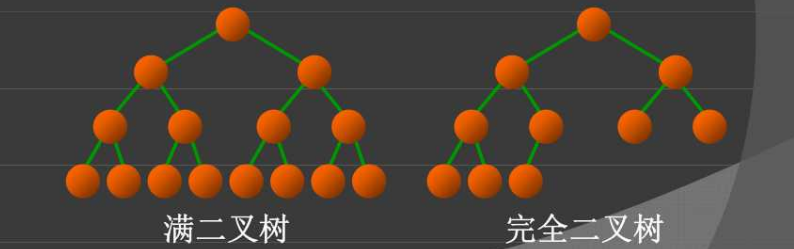
- 满二叉树
- 完全二叉树：k层二叉树除了第k层有从有向左的连续缺失的结点
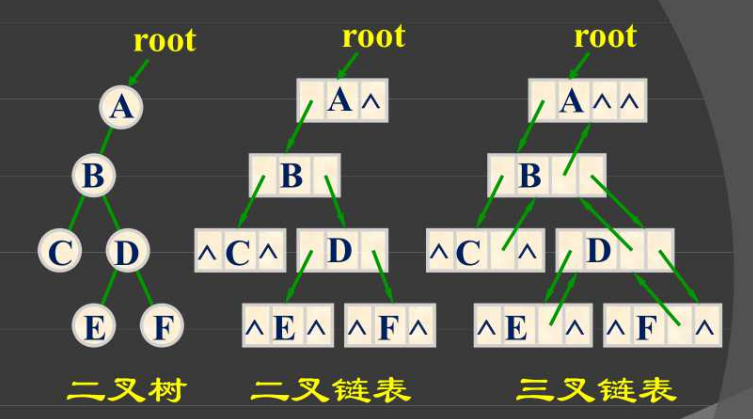
- 二叉树的顺序表示
- 按照满二叉树的顺序，有数则填，无数则留空
- 极端情况下，资源利用率特别低
- 二叉树的链式表示
- 二叉链表
- 三叉链表
- 二叉树遍历
- 前序遍历（VLR）【-+a*b-cd/ef】
- 中序遍历（LVR）【a+b*c-d-e/f】
- 后序遍历（LRV）【abcd-*+ef/-】
- 线索化二叉树
- 经过事先预处理后，将某种遍历顺序下的前驱后继关系记录。
- 树转化为二叉树
一般树转换为二叉树表示就是用树的孩子、兄弟表示来存储树的结构
- 在所有的兄弟结点间加一条连线
- 对每个结点，保留与其长子的连线外，去掉和其他孩子的连线
- 森林转化为二叉树
- 把每棵树变为二叉树
- 将各个二叉树的根节点视为兄弟连在一起
- 树的先根次序遍历
- 访问根节点
- 依次先根遍历根的各棵子树
- 结果和对应的二叉树的前序遍历相同
- 树的后根次序遍历
- 依次后根遍历根的各棵子树
- 访问根节点
- 结果和对应二叉树的中序遍历相同
- 森林的先根次序遍历
- 森林的后根次序遍历
- Huffman树
- 两个结点之间的路径长度，是连接两结点的路径上的分支数
- 树的路径长度是各结点到根结点的路径长度之和
- 完全二叉树或理想平衡树满足路径长度最小的要求
- Huffman树带权路径
- 带权后，平衡树不一定是路径长度最小值的满足条件