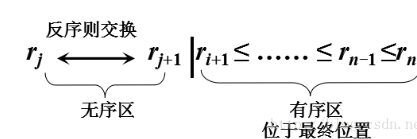最近在研究一些经常用到的东西想把它们做一个汇总,想了想用到最多的应该是排序算法,所以对排序算法做了个总结
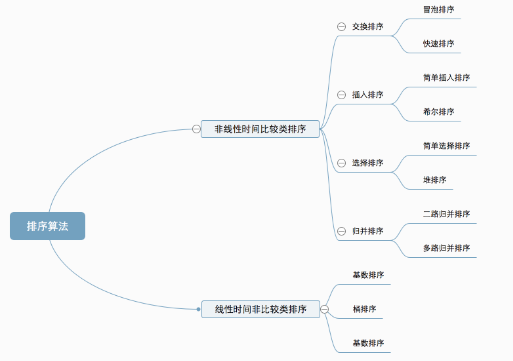
十种常见排序算法可以分为两大类:
非线性时间比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此称为非线性时间比较类排序。
线性时间非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此称为线性时间非比较类排序。
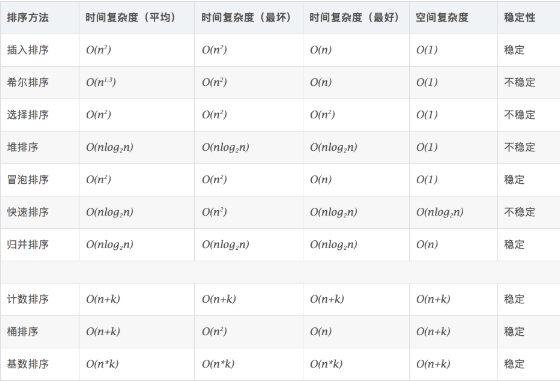
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
**空间复杂度:**是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便,就让第一个数6作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在6的右边,比基准数小的数放在6的左边,类似下面这种排列:
3 1 2 5 4 6 9 7 10 8
在初始状态下,数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置,假设这个位置是k。现在就需要寻找这个k,并且以第k位为分界点,左边的数都小于等于6,右边的数都大于等于6,递归对左右两个区间进行同样排序即可。想一想,你有办法可以做到这点吗?这就是快速排序所解决的问题。
快速排序是C.R.A.Hoare于1962年提出的一种划分交换排序。它采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。它的平均时间复杂度为O(nlogn),最坏时间复杂度为O(n^2).
首先上图:
从图中我们可以看到:
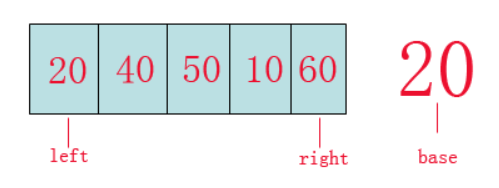
left指针,right指针,base参照数。
其实思想是蛮简单的,就是通过第一遍的遍历(让left和right指针重合)来找到数组的切割点。
第一步:首先我们从数组的left位置取出该数(20)作为基准(base)参照物。(如果是选取随机的,则找到随机的哨兵之后,将它与第一个元素交换,开始普通的快排)
第二步:从数组的right位置向前找,一直找到比(base)小的数,如果找到,将此数赋给left位置(也就是将10赋给20),此时数组为:10,40,50,10,60, left和right指针分别为前后的10。
第三步:从数组的left位置向后找,一直找到比(base)大的数,如果找到,将此数赋给right的位置(也就是40赋给10),此时数组为:10,40,50,40,60, left和right指针分别为前后的40。
第四步:重复“第二,第三“步骤,直到left和right指针重合,最后将(base)放到40的位置, 此时数组值为: 10,20,50,40,60,至此完成一次排序。
第五步:此时20已经潜入到数组的内部,20的左侧一组数都比20小,20的右侧作为一组数都比20大, 以20为切入点对左右两边数按照"第一,第二,第三,第四"步骤进行,最终快排大功告成。
快速排序代码如下:
1 //快速排序,随机选取哨兵放前面
2 void QuickSort(int* h, int left, int right)
3 {
4 if(h==NULL) return;
5 if(left>=right) return;
6
7 //防止有序队列导致快速排序效率降低
8 srand((unsigned)time(NULL));
9 int len=right-left;
10 int kindex=rand()%(len+1)+left;
11 Swap(h[left],h[kindex]);
12
13 int key=h[left],i=left,j=right;
14 while(i<j)
15 {
16 while(h[j]>=key && i<j) --j;
17 if(i<j) h[i]=h[j];
18 while(h[i]<key && i<j) ++i;
19 if(i<j) h[j]=h[i];
20 }
21
22 h[i]=key;
23
24 //QuickSort(&h[left],0,i-1);
25 //QuickSort(&h[j+1],0,right-j-1);
26
27 QuickSort(h,left,i-1);
28 QuickSort(h,j+1,right);
29 }冒泡排序在扫描过程中两两比较相邻记录,如果反序则交换,最终,最大记录就被“沉到”了序列的最后一个位置,第二遍扫描将第二大记录“沉到”了倒数第二个位置,重复上述操作,直到n-1 遍扫描后,整个序列就排好序了。
1 //冒泡排序
2 void BubbleSort(int* h, size_t len)
3 {
4 if(h==NULL) return;
5 if(len<=1) return;
6 //i是次数,j是具体下标
7 for(int i=0;i<len-1;++i)
8 for(int j=0;j<len-1-i;++j)
9 if(h[j]>h[j+1])
10 Swap(h[j],h[j+1]);
11
12 return;
13 } 选择排序也是一种简单直观的排序算法。它的工作原理很容易理解:初始时在序列中找到最小(大)元素,放到序列的起始位置作为已排序序列;然后,再从剩余未排序元素中继续寻找最小(大)元素,放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
注意选择排序与冒泡排序的区别:冒泡排序通过依次交换相邻两个顺序不合法的元素位置,从而将当前最小(大)元素放到合适的位置;而选择排序每遍历一次都记住了当前最小(大)元素的位置,最后仅需一次交换操作即可将其放到合适的位置。
1 //选择排序
2 void SelectionSort(int* h, size_t len)
3 {
4 if(h==NULL) return;
5 if(len<=1) return;
6
7 int minindex,i,j;
8 //i是次数,也即排好的个数;j是继续排
9 for(i=0;i<len-1;++i)
10 {
11 minindex=i;
12 for(j=i+1;j<len;++j)
13 {
14 if(h[j]<h[minindex]) minindex=j;
15 }
16 Swap(h[i],h[minindex]);
17 }
18
19 return;
20 }直接插入排序(straight insertion sort),有时也简称为插入排序(insertion sort),是减治法的一种典型应用。其基本思想如下:
- 对于一个数组A[0,n]的排序问题,假设认为数组在A[0,n-1]排序的问题已经解决了。
- 考虑A[n]的值,从右向左扫描有序数组A[0,n-1],直到第一个小于等于A[n]的元素,将A[n]插在这个元素的后面。
很显然,基于增量法的思想在解决这个问题上拥有更高的效率。
直接插入排序对于最坏情况(严格递减的数组),需要比较和移位的次数为n(n-1)/2;对于最好的情况(严格递增的数组),需要比较的次数是n-1,需要移位的次数是0。当然,对于最好和最坏的研究其实没有太大的意义,因为实际情况下,一般不会出现如此极端的情况。然而,直接插入排序对于基本有序的数组,会体现出良好的性能,这一特性,也给了它进一步优化的可能性。(希尔排序)。直接插入排序的时间复杂度是O(n^2),空间复杂度是O(1),同时也是稳定排序。
下面用一个具体的场景,直观地体会一下直接插入排序的过程:
场景:
现有一个无序数组,共7个数:89 45 54 29 90 34 68。
使用直接插入排序法,对这个数组进行升序排序。
89 45 54 29 90 34 68
45 89 54 29 90 34 68
45 54 89 29 90 34 68
29 45 54 89 90 34 68
29 45 54 89 90 34 68
29 34 45 54 89 90 68
29 34 45 54 68 89 90
算法实现:
1 //插入排序
2 void InsertSort(int* h, size_t len)
3 {
4 if(h==NULL) return;
5 if(len<=1) return;
6
7 int i,j;
8 //i是次数,也即排好的个数;j是继续排
9 for(i=1;i<len;++i)
10 for(j=i;j>0;--j)
11 if(h[j]<h[j-1]) Swap(h[j],h[j-1]);
12 else break;
13
14 return;
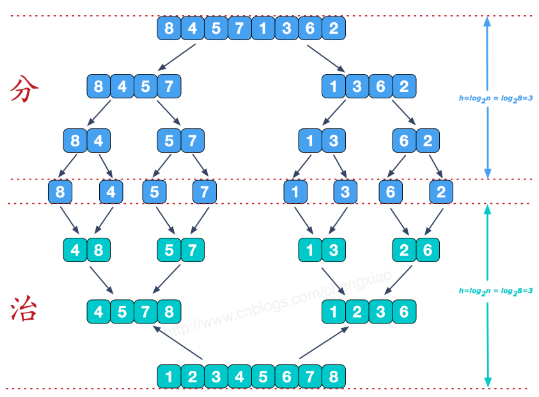
15 }归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而**治(conquer)**的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
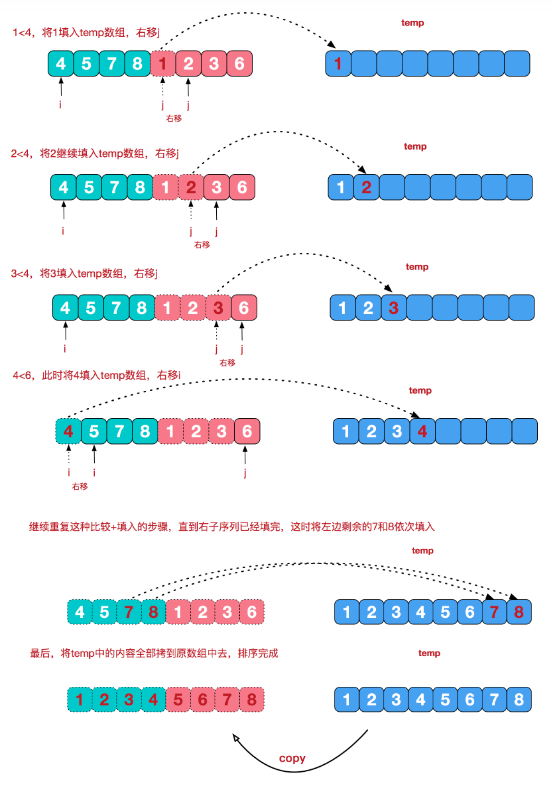
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
1 //归并排序
2 void MergeArray(int* arr, size_t left, size_t mid, size_t right, int* temp)
3 {
4 if(arr==NULL) return;
5
6 size_t i=left,j=mid+1,k=0;
7 while(i<=mid && j<=right)
8 {
9 if(arr[i]<=arr[j])
10 {
11 temp[k++]=arr[i++];
12 continue;
13 }
14
15 temp[k++]=arr[j++];
16 }
17
18 while(i<=mid)
19 temp[k++]=arr[i++];
20
21 while(j<=right)
22 temp[k++]=arr[j++];
23
24 memcpy(&arr[left],temp,k*sizeof(int));
25
26 return;
27 }
28
29 void MMergeSort(int* arr, size_t left, size_t right, int* temp)
30 {
31 if(left<right)
32 {
33 size_t mid=(left+right)/2;
34 MMergeSort(arr, left, mid, temp);
35 MMergeSort(arr, mid+1,right, temp);
36 MergeArray(arr,left, mid, right, temp);
37 }
38 }
39
40 void MergeSort(int* h, size_t len)
41 {
42 if(h==NULL) return;
43 if(len<=1) return;
44 int* temp=(int*)calloc(len,sizeof(int));
45 MMergeSort(h, 0, len-1, temp);
46
47 memcpy(h,temp,sizeof(int)*len);
48
49 free(temp);
50
51 return;
52 }希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。本文会以图解的方式详细介绍希尔排序的基本思想及其代码实现。
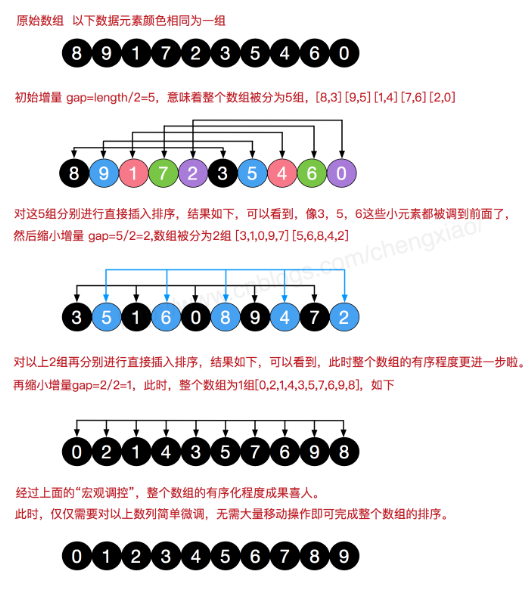
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
简单插入排序很循规蹈矩,不管数组分布是怎么样的,依然一步一步的对元素进行比较,移动,插入,比如[5,4,3,2,1,0]这种倒序序列,数组末端的0要回到首位置很是费劲,比较和移动元素均需n-1次。而希尔排序在数组中采用跳跃式分组的策略,通过某个增量将数组元素划分为若干组,然后分组进行插入排序,随后逐步缩小增量,继续按组进行插入排序操作,直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序,小的基本在前,大的基本在后。然后缩小增量,到增量为1时,其实多数情况下只需微调即可,不会涉及过多的数据移动。
我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2...1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
1 //希尔排序
2 void ShellSort(int* h, size_t len)
3 {
4 if(h==NULL) return;
5 if(len<=1) return;
6
7 for(int div=len/2;div>=1;div/=2)
8 for(int k=0;k<div;++k)
9 for(int i=div+k;i<len;i+=div)
10 for(int j=i;j>k;j-=div)
11 if(h[j]<h[j-div]) Swap(h[j],h[j-div]);
12 else break;
13
14 return;
15 } 堆排序实际上是利用堆的性质来进行排序的,要知道堆排序的原理我们首先一定要知道什么是堆。
堆的定义:
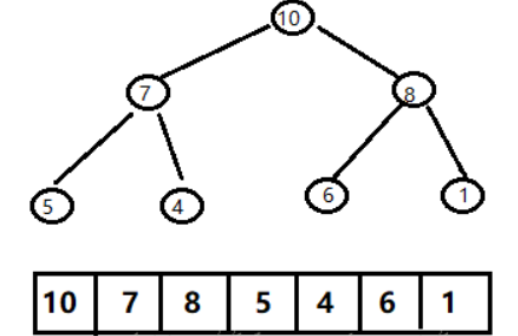
堆实际上是一棵完全二叉树。
堆满足两个性质:
1、堆的每一个父节点都大于(或小于)其子节点;
2、堆的每个左子树和右子树也是一个堆。
堆的分类:
堆分为两类:
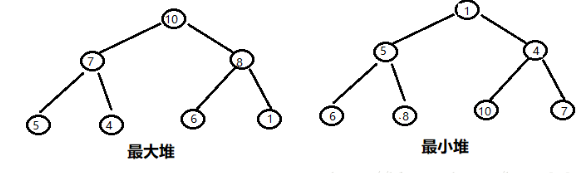
1、最大堆(大顶堆):堆的每个父节点都大于其孩子节点;
2、最小堆(小顶堆):堆的每个父节点都小于其孩子节点;
1 //堆排序
2 /*
3 大顶堆sort之后,数组为从小到大排序
4 */
5 //====调整=====
6 void AdjustHeap(int* h, int node, int len) //----node为需要调整的结点编号,从0开始编号;len为堆长度
7 {
8 int index=node;
9 int child=2*index+1; //左孩子,第一个节点编号为0
10 while(child<len)
11 {
12 //右子树
13 if(child+1<len && h[child]<h[child+1])
14 {
15 child++;
16 }
17 if(h[index]>=h[child]) break;
18 Swap(h[index],h[child]);
19 index=child;
20 child=2*index+1;
21 }
22 }
23
24
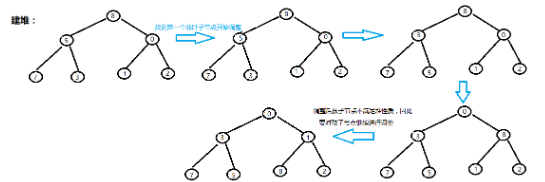
25 //====建堆=====
26 void MakeHeap(int* h, int len)
27 {
28 for(int i=len/2;i>=0;--i)
29 {
30 AdjustHeap(h, i, len);
31 }
32 }
33
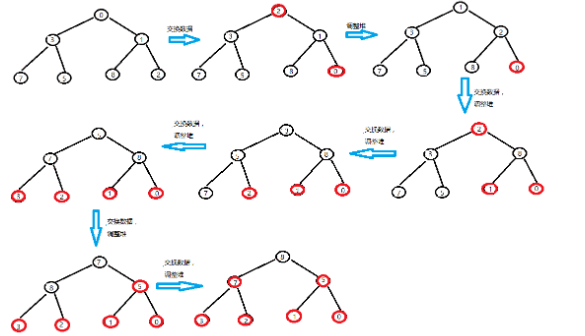
34 //====排序=====
35 void HeapSort(int* h, int len)
36 {
37 MakeHeap(h, len);
38 for(int i=len-1;i>=0;--i)
39 {
40 Swap(h[i],h[0]);
41 AdjustHeap(h, 0, i);
42 }
43 }基数排序与本系列前面讲解的七种排序方法都不同,它不需要比较关键字的大小。
它是根据关键字中各位的值,通过对排序的N个元素进行若干趟“分配”与“收集”来实现排序的。
不妨通过一个具体的实例来展示一下,基数排序是如何进行的。
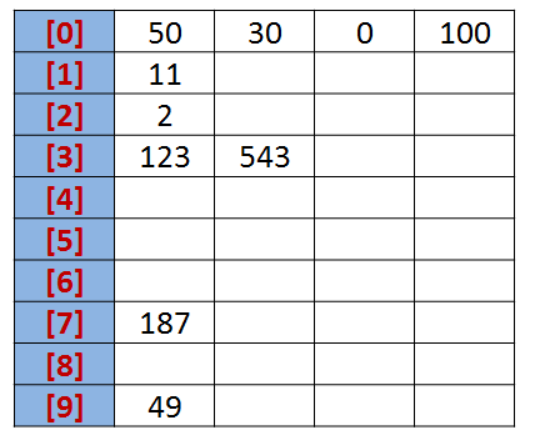
设有一个初始序列为: R {50, 123, 543, 187, 49, 30, 0, 2, 11, 100}。
我们知道,任何一个阿拉伯数,它的各个位数上的基数都是以0~9来表示的。
所以我们不妨把0~9视为10个桶。
我们先根据序列的个位数的数字来进行分类,将其分到指定的桶中。例如:R[0] = 50,个位数上是0,将这个数存入编号为0的桶中。
分类后,我们在从各个桶中,将这些数按照从编号0到编号9的顺序依次将所有数取出来。
这时,得到的序列就是个位数上呈递增趋势的序列。
按照个位数排序: {50, 30, 0, 100, 11, 2, 123, 543, 187, 49}。
接下来,可以对十位数、百位数也按照这种方法进行排序,最后就能得到排序完成的序列。
1 int GetMaxDight(int* h, int len)
2 {
3 if(h==NULL) return 0;
4 if(len<1) return 0;
5
6 int max=h[0];
7 for(int i=1;i<len;++i)
8 {
9 if(h[i]>max) max=h[i];
10 }
11
12 int digit=1;
13 while(max/10!=0)
14 {
15 max/=10;
16 ++digit;
17 }
18
19 return digit;
20 }
21
22 int GetReminder(int value,int digit)
23 {
24 int div=1;
25 for(int i=1;i<digit;++i)
26 div*=10;
27
28 return value/div%10;
29 }
30
31 void RadixSort_LSD(int* h, int len)
32 {
33 if(h==NULL) return;
34 if(len<=1) return;
35
36 int digit=GetMaxDight(h,len);
37 //printf("MaxDigit:%d\n", digit);
38
39 int count[10]={0};
40 int *tmp=(int*)calloc(len,sizeof(int));
41
42 for(int d=1;d<=digit;++d)
43 {
44 memset(count,0,sizeof(count));
45
46 for(int i=0;i<len;++i)
47 {
48 count[GetReminder(h[i],d)]++;
49 }
50
51 //求右边界
52 for(int i=1;i<10;++i)
53 {
54 count[i]+=count[i-1];
55 }
56
57 for(int i=len-1;i>=0;--i)
58 {
59 int r=GetReminder(h[i],d);
60 int index=count[r];
61 tmp[index-1]=h[i];
62 count[r]--;
63 }
64
65 memcpy(h,tmp,len*sizeof(int));
66 }
67
68 free(tmp);
69 }
70
71 void RadixSort_LSD_Reverse(int* h, int len)
72 {
73 if(h==NULL) return;
74 if(len<=1) return;
75
76 int digit=GetMaxDight(h,len);
77 //printf("MaxDigit:%d\n", digit);
78
79 int count[10]={0};
80
81 int *tmp=(int*)calloc(len,sizeof(int));
82
83 for(int d=1;d<=digit;++d)
84 {
85 memset(count,0,sizeof(count));
86
87 for(int i=0;i<len;++i)
88 {
89 count[GetReminder(h[i],d)]++;
90 }
91
92 //printf("haha\n");
93
94 //求右边界
95 for(int i=8;i>=0;--i)
96 {
97 count[i]+=count[i+1];
98 }
99
100
101
102 for(int i=len-1;i>=0;--i)
103 {
104 int r=GetReminder(h[i],d);
105 int index=count[r];
106 tmp[index-1]=h[i];
107 count[r]--;
108 }
109
110 memcpy(h,tmp,len*sizeof(int));
111 }
112
113 free(tmp);
114 }下面我们直接来介绍MSD基数排序的步骤。
MSD基数排序是从最高位开始对序列进行分组,到最低位为止。但是其实现过程是和LSD基数排序不同的,排序过程中需要用到递归函数。
待排序序列
170, 45, 75, 90, 2, 24, 802, 66
我们看到,这里面的最大的数是3位数。所以说我们开始从百位对这些数进行分组
0: 045, 075, 090,002, 024, 066 1: 170 2-7: 空 8: 802 9: 空
从这里开始就和LSD基数排序有差别了。在LSD基数排序中,每次分好组以后开始对桶中的数据进行收集。然后根据下一位,对收集后的序列进行分组。而对于MSD,在这里不会对桶中的数据进行收集。我们要做的是检测每个桶中的数据。当桶中的元素个数多于1个的时候,要对这个桶递归进行下一位的分组。
在这个例子中,我们要对0桶中的所有元素根据十位上的数字进行分组
0: 002 1: 空 2: 024 3: 空 4: 045 5: 空 6: 066 7: 075 8: 空 9: 090
按照上面所说,我们应该再递归的对每个桶中的元素根据个位上的数进行分组。但是我们发现,现在在每个桶中的元素的个数都是小于等于1的。因此,到这一步我们就开始回退了。也就是说我们开始收集桶中的数据。收集完成以后,回退到上一层。此时按照百位进行分组的桶变成了如下的形式
0: 002, 024, 045,066, 075, 090 1: 170 2-7: 空 8: 802 9: 空
然后我们在对这个桶中的数据进行收集。收集起来以后序列如下
2, 24, 45, 66, 75, 90, 170, 802
整个MSD基数排序就是按照上面的过程进行的。
在我对MSD基数排序步骤进行叙述的时候,中间递归函数的过程可能叙述的不够清楚。我个人建议对递归函数不了解的可以先了解一下递归函数的原理,然后再回来看这个过程可能对MSD基数排序过程更容易理解。
1 int GetMaxDight(int* h, int len)
2 {
3 if(h==NULL) return 0;
4 if(len<1) return 0;
5
6 int max=h[0];
7 for(int i=1;i<len;++i)
8 {
9 if(h[i]>max) max=h[i];
10 }
11
12 int digit=1;
13 while(max/10!=0)
14 {
15 max/=10;
16 ++digit;
17 }
18
19 return digit;
20 }
21
22 int GetReminder(int value,int digit)
23 {
24 int div=1;
25 for(int i=1;i<digit;++i)
26 div*=10;
27
28 return value/div%10;
29 }
30
31 void RRadixSort_MSD(int* h, int begin, int end, int digit)
32 {
33 if(h==NULL) return;
34 if(begin>=end) return;
35 if(digit<1) return;
36
37 int start[10];
38 int count[10]={0};
39 int *tmp=(int*)calloc(end-begin+1,sizeof(int));
40
41 for(int i=begin;i<=end;++i)
42 {
43 count[GetReminder(h[i],digit)]++;
44 }
45
46 memcpy(start,count,sizeof(start));
47
48 //求右边界
49 for(int i=1;i<10;++i)
50 {
51 start[i]+=start[i-1];
52 }
53
54 for(int i=end;i>=begin;--i)
55 {
56 int r=GetReminder(h[i],digit);
57 int index=start[r];
58 tmp[index-1]=h[i];
59 start[r]--;
60 }
61
62 /*
63 for(int i=0;i<10;++i)
64 {
65 printf("%d ",start[i]);
66 }
67
68 printf("\n");
69 */
70
71 memcpy(&h[begin],tmp,(end-begin+1)*sizeof(int));
72
73 for(int i=0;i<10;++i)
74 {
75 if(count[i]>1)
76 {
77 RRadixSort_MSD(h, start[i], start[i]+count[i]-1, digit-1);
78 }
79 }
80 }
81
82 void RadixSort_MSD(int* h, int len)
83 {
84 if(h==NULL) return;
85 if(len<=1) return;
86
87 int digit=GetMaxDight(h,len);
88
89 //printf("MaxDigit:%d\n",digit);
90
91 RRadixSort_MSD(h, 0, len-1, digit);
92 }
93
94 void RRadixSort_MSD_Reverse(int* h, int begin, int end, int digit)
95 {
96 if(h==NULL) return;
97 if(begin>=end) return;
98 if(digit<1) return;
99
100 int start[10];
101 int count[10]={0};
102 int *tmp=(int*)calloc(end-begin+1,sizeof(int));
103
104 for(int i=begin;i<=end;++i)
105 {
106 count[GetReminder(h[i],digit)]++;
107 }
108
109 memcpy(start,count,sizeof(start));
110
111 //求右边界
112 for(int i=8;i>=0;--i)
113 {
114 start[i]+=start[i+1];
115 }
116
117 for(int i=end;i>=begin;--i)
118 {
119 int r=GetReminder(h[i],digit);
120 int index=start[r];
121 tmp[index-1]=h[i];
122 start[r]--;
123 }
124
125 /*
126 for(int i=0;i<10;++i)
127 {
128 printf("%d ",start[i]);
129 }
130
131 printf("\n");
132 */
133
134 memcpy(&h[begin],tmp,(end-begin+1)*sizeof(int));
135
136 for(int i=0;i<10;++i)
137 {
138 if(count[i]>1)
139 {
140 RRadixSort_MSD_Reverse(h, start[i], start[i]+count[i]-1, digit-1);
141 }
142 }
143 }
144
145 void RadixSort_MSD_Reverse(int* h, int len)
146 {
147 if(h==NULL) return;
148 if(len<=1) return;
149
150 int digit=GetMaxDight(h,len);
151
152 //printf("MaxDigit:%d\n",digit);
153
154 RRadixSort_MSD_Reverse(h, 0, len-1, digit);
155 } 1 void Swap(int& a, int& b)
2 {
3 int t=a;
4 a=b;
5 b=t;
6
7 return;
8 }
9
10 int main()
11 {
12 int A[10]={0};
13 srand((unsigned)time(NULL));
14
15 printf("before:\n");
16 for(int i=0;i<10;++i)
17 {
18 A[i]=rand()%100;
19 printf("%d ",A[i]);
20 }
21 printf("\n");
22
23 printf("after:\n");
24 //QuickSort(A,0,9);
25 //BubbleSort(A,sizeof(A)/sizeof(int));
26 //SelectionSort(A,sizeof(A)/sizeof(int));
27 //InsertSort(A,sizeof(A)/sizeof(int));
28 //MergeSort(A,sizeof(A)/sizeof(int));
29 //ShellSort(A,sizeof(A)/sizeof(int));
30 //HeapSort(A,sizeof(A)/sizeof(int));
31 //RadixSort_LSD(A,sizeof(A)/sizeof(int));
32 //RadixSort_MSD(A,sizeof(A)/sizeof(int));
33 //RadixSort_LSD_Reverse(A,sizeof(A)/sizeof(int));
34 RadixSort_MSD_Reverse(A,sizeof(A)/sizeof(int));
35 for(int i=0;i<sizeof(A)/sizeof(int);++i)
36 {
37 printf("%d ",A[i]);
38 }
39 printf("\n");
40
41 return 0;
42 }