README.md

KryPy

KryPy is a Python 3 module for Krylov subspace methods for the solution of linear algebraic systems. This includes enhanced versions of CG, MINRES and GMRES as well as methods for the efficient solution of sequences of linear systems.

Features

KryPy gives you an easy-to-use yet flexible interface to Krylov subspace methods for linear algebraic systems. Compared to the implementations in SciPy (or MATLAB), KryPy allows you to supply additional arguments that may help you to tune the solver for the specific problem you want to solve. The additional arguments may also be of interest if you are doing research on Krylov subspace methods.

Some features of KryPy are:

• User-defined inner products - useful when solving a linear algebraic system whose operator is self-adjoined in a non-Euclidean inner-product. This way, CG or MINRES can be applied to self-adjoined (but non-symmetric/non-Hermitian) operators easily.
• Full control of preconditioners - the order of applying preconditioners matters. This is why you can supply two left preconditioners (one of whom implicitly changes the inner product and thus has to be positive definite) and one right preconditioner. Take a look at the arguments M, Ml and Mr.
• Get the Arnoldi/Lanczos basis and Hessenberg matrix - you want to extract further information from the generated vectors (e.g. recycling)? Just pass the optional argument store_arnoldi=True.
• Explicitly computed residuals on demand - if you do research on Krylov subspace methods or preconditioners, then you sometimes want to know the explicitly computed residual in each iteration (in contrast to an updated residual which can be obtained implicitly). Then you should pass the optional argument explicit_residual=True.
• Compute errors - if you have (for research purposes) the exact solution at hand and want to monitor the error in each iteration instead of the residual, you can supply the optional argument exact_solution=x_exact to the LinearSystem.

Usage

Documentation

The documentation is hosted at krypy.readthedocs.org.

Example

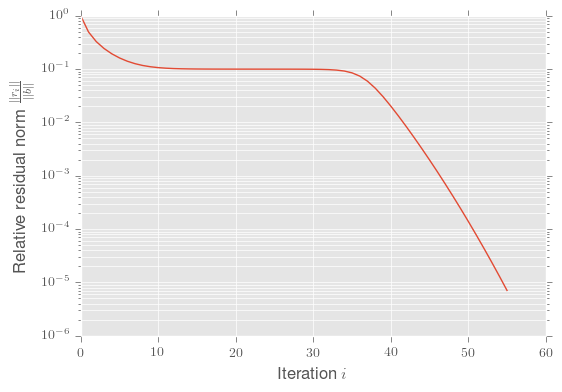
The above convergence history is obtained with the following example where the Gmres method is used to solve the linear system A*x=b with the diagonal matrix A=diag(1e-3,2,...,100) and right hand side b=[1,...,1].

import numpy
import krypy

A = numpy.diag([1.0e-3] + list(range(2, 101)))
b = numpy.ones(100)

# sol, out = krypy.cg(A, b)
# sol, out = krypy.minres(A, b)
sol, out = krypy.gmres(A, b)

# sol is None if no solution has been found
# out.resnorms the relative residual norms and some more data

# plot residuals
import matplotlib.pyplot as plt
plt.semilogy(out.resnorms)
plt.show()

Of course, this is just a toy example where you would not use GMRES in practice. KryPy can handle arbitrary large matrices - as long as the (hopefully sparse) matrices and the generated basis of the Krylov subspace fit into your memory. ;) Furthermore, in actual applications, you definitely want to adjust Gmres' parameters such as the residual tolerance.

Help

Help can be optained via Python's builtin help system. For example, you can use the ? in ipython:

from krypy.linsys import Gmres
?Gmres

Installing

pip / PyPi

Simply run pip install krypy.

Ubuntu

There's an Ubuntu PPA with packages for Python 2 and Python 3.

Installing from source

KryPy has the following dependencies:

• NumPy
• SciPy

Development

KryPy is currently maintained by André Gaul. Feel free to contact André. Please submit feature requests and bugs as github issues.

KryPy is developed with continuous integration. Current status:

Distribution

To create a new release

1. bump the __version__ number,

2. create a Git tag,

   $ git tag -a v0.3.1
   $ git push --tags
   

   and

3. upload to PyPi:

   $ make upload
   

License

KryPy is free software licensed under the MIT License.

References

KryPy evolved from the PyNosh package (Python framework for nonlinear Schrödinger equations; joint work with Nico Schlömer) which was used for experiments in the following publication:

• Preconditioned Recycling Krylov subspace methods for self-adjoint problems, A. Gaul and N. Schlömer, arxiv: 1208.0264, 2012