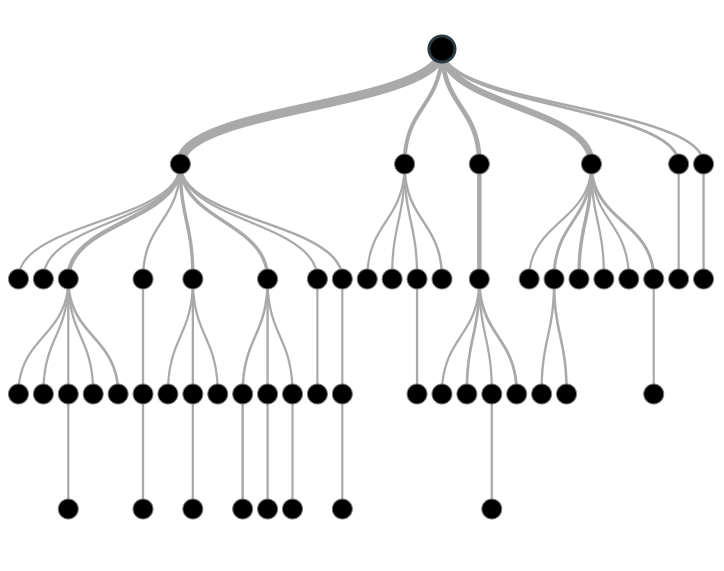
Recall in data structures learning about the different types of tree structures - binary, red black, and splay trees. In tree based modeling, we work off these structures for classification prediction.
Tree based machine learning is great because it's incredibly accurate and stable, as well as easy to interpret. Despite being a linear model, tree based models map non-linear relationships well. The general structure is as follows:
Decision trees are a type of supervised learning algorithm used in classification that works for both categorical and continuous input/output variables. This typle of model includes structures with nodes which represent tests on attributes and the end nodes (leaves) of each branch represent class labels. Between these nodes are what we call edges, which represent a 'decision' that separates the data from the previous node based on some criteria.
Looks familiar, right?
As mentioned above, nodes are an important part of the structure of Decision Trees. In this section, we'll review different types of nodes.
The root node is the node at the very top. It represents an entire population or sample because it has yet to be divided by any edges.
Decision Nodes are the nodes that occur between the root node and leaves of your decision tree. It's considered a decision node because it's a resulting node of an edge that then splits once again into either more decision nodes, or the leaves.
As mentioned before, leaves are the final nodes at the bottom of the decision tree that represent a class label in classification. They're also called terminal nodes because more nodes do not split off of them.
A node, which is divided into sub-nodes is called parent node of sub-nodes where as sub-nodes are the child of parent node.
-
Easy to Understand: Decision tree output is fairly easy to understand since it doesn't require any statistical knowledge to read and interpret them. Its graphical representation is very intuitive and users can easily relate their hypothesis.
-
Useful in Data exploration: Decision tree is one of the fastest way to identify most significant variables and relation between two or more variables. With the help of decision trees, we can create new variables / features that has better power to predict target variable. You can refer article (Trick to enhance power of regression model) for one such trick. It can also be used in data exploration stage. For example, we are working on a problem where we have information available in hundreds of variables, there decision tree will help to identify most significant variable.
-
Less data cleaning required: It requires less data cleaning compared to some other modeling techniques. It is not influenced by outliers and missing values to a fair degree.
-
Data type is not a constraint: It can handle both numerical and categorical variables.
-
Non Parametric Method: Decision tree is considered to be a non-parametric method. This means that decision trees have no assumptions about the space distribution and the classifier structure.
-
Over fitting: Over fitting is one of the most practical difficulty for decision tree models. This problem gets solved by setting constraints on model parameters and pruning (discussed in detailed below).
-
Not fit for continuous variables: While working with continuous numerical variables, decision tree looses information when it categorizes variables in different categories.
In this output, the rows show result for trees with different numbers of nodes. The column xerror represents the cross-validation error and the CP represents the complexity parameter.
Decision Tree pruning is a technique that reduces the size of decision trees by removing sections (nodes) of the tree that provide little power to classify instances. This is great because it reduces the complexity of the final classifier, which results in increased predictive accuracy by reducing overfitting.
Ultimately, our aim is to reduce the cross-validation error. First, we index with the smallest complexity parameter:
Recall the ensemble learning method from the Optimization lecture. Random Forests are an ensemble learning method for classification and regression. It works by combining individual decision trees through bagging. This allows us to overcome overfitting.
First, we create many decision trees through bagging. Once completed, we inject randomness into the decision trees by allowing the trees to grow to their maximum sizes, leaving them unpruned.
We make sure that each split is based on randomly selected subset of attributes, which reduces the correlation between different trees.
Now we get into the random forest by voting on categories by majority. We begin by splitting the training data into K bootstrap samples by drawing samples from training data with replacement.
Next, we estimate individual trees ti to the samples and have every regression tree predict a value for the unseen data. Lastly, we estimate those predictions with the formula:
where ŷ is the response vector and x = [x1,...,xN]T ∈ X as the input parameters.
Random Forests allow us to learn non-linearity with a simple algorithm and good performance. It's also a fast training algorithm and resistant to overfitting.
What's also phenomenal about Random Forests is that increasing the number of trees decreases the variance without increasing the bias, so the worry of the variance-bias tradeoff isn't as present.
The averaging portion of the algorithm also allows the real structure of the data to reveal. Lastly, the noisy signals of individual trees cancel out.
Unfortunately, random forests have high memory consumption because of the many tree constructions. There's also little performance gain from larger training datasets.
==========================================================================================
TThis guide was written in Python 3.6.
Let's install the modules we'll need for this tutorial. Open up your terminal and enter the following commands to install the needed python modules:
pip3 install scipy
pip3 install numpy
Ensemble Learning allows us to combine predictions from different multiple learning algorithms. This is what we consider to be the "ensemble". By doing this, we can have a result with a better predictive performance compared to a single learner.
It's important to note that one drawback is that there's increased computation time and reduces interpretability.
Bagging is a technique where reuse the same training algorithm several times on different subsets of the training data.
Given a training dataset D of size N, bagging will generate new training sets Di of size M by sampling with replacement from D. Some observations might be repeated in each Di.
If we set M to N, then on average 63.2% of the original dataset D is represented, the rest will be duplicates.
The final step is that we train the classifer C on each Ci separately.
Boosting is an optimization technique that allows us to combine multiple classifiers to improve classification accuracy. In boosting, none of the classifiers just need to be at least slightly better than chance.
Boosting involves training classifiers on a subset of the training data that is most informative given the current classifiers.
The general boosting algorithm first involves fitting a simple model to subsample of the data. Next, we identify misclassified observations (ones that are hard to predict). we focus subsequent learners on these samples to get them right. Lastly, we combine these weak learners to form a more complex but accurate predictor.
Now, instead of resampling, we can reweight misclassified training examples:
Aside from its easy implementation, AdaBoosting is great because it's a simple combination of multiple classifiers. These classifiers can also be different.
On the other hand, AdaBoost is sensitive to misclassified points in the training data.