hd_log_reg_rmarkdown.Rmd

---
title: "Heart Disease UCI - Logistic Regression"
author: "Dany Park"
date: "11/02/2021"
output: rmarkdown::github_document
---

# Logistic Regression and Prediction of Heart Disease
The project is to apply logistic regression to the heart disease datatset and apply the fitted model to predict the potential patient.

## 1. Overview of Logistic Regression
Consider a dataset with the response variable(Y) falls into two categories. Logistic regression is a statistical model that focuses on the probability of each Y variable's class given values of the independent variables(X). Since the model is based on the probability, at any given X value, the result has to fall between 0 and 1. Mathematically speaking, 0 ≤ P(X) ≤ 1. The value of P(X) should always produce the outputs within the range. 

![Logistic Regression](https://www.dotnetlovers.com/Images/LogisticRegressionFormula1020201890212AM.png)

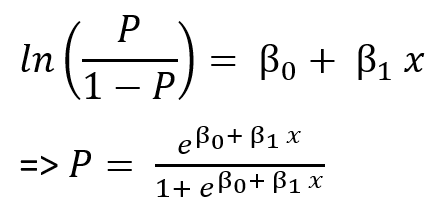
The regression is fitted using the maximum likelihood method because of its statistical properties. The method estimates the model's coefficients such that the predicted probability corresponds as closely as possible to the individual's observations. In other words, predicted β0 and β1 are found such that plugging these estimates into p(X), yields a number close to one for all individuals who defaulted, and a number close to zero for all individuals who did not¹.

## 2. The Dataset 
The original [dataset](https://archive.ics.uci.edu/ml/datasets/Heart+Disease) from UCI contained 76 attributes which represent a patient's condition. The dataset for this article is from [Kaggle - Heart Disease UCI](https://www.kaggle.com/ronitf/heart-disease-uci). The subset of 14 attributes with every incident represents a patient.

| Attribute | Description |
| :---: | :---: |
| target | Patients with heart disease, Response variable |
| age | Age of patients |
| sex | Gender of patients |
| cp | chest pain type (4 values) |
| trestbps | resting blood pressure |
| sr | serum cholestoral in mg/dl |
| fbs | fasting blood sugar > 120 mg/dl |
| restang | resting electrocardiographic results (values 0,1,2) |
| hr | maximum heart rate achieved |
| exang | exercise induced angina |
| oldpeak | ST depression induced by exercise relative to rest |
| slope | the slope of the peak exercise ST segment |
| fbs | number of major vessels (0-3) colored by flourosopy |
| thal | 3 = normal; 6 = fixed defect; 7 = reversable defect |

The data is imported from the local device and printed summary of the dataframe to get the overview. 
```{r Importation, echo=TRUE}
#import dataframe: csv
df<-read.csv("heart.csv", header =TRUE)
summary(df)
head(df,5)
```
The dataset has a total of 14 attributes and 303 incidences. Of those, `sex`, `cp`, `fbs`, `restecg`, `exang`, `slope`, `thal` and `target` are the characterized as categorical variable. The rest, `age`, `trestbps`, `chol`, `thalach` and `oldpeak`, are the continuous variable. However, before we proceed, there's an erroneous attribute: `ï..age`. It is corrected to `age`. 
```{r Attribute name change, echo=TRUE}
#change erronous attribute name:  ï..age
colnames(df)[colnames(df)=='ï..age'] <-'age'
head(df,5)
```
Most of the time, the categorical variable in the dataframe requires to be converted to the factor type in Rstudio. Initially, all the variables were categorized as an integer. Before analyzing the data, categorical variables must be converted from int to factor. The code `as.factor` is used to change the type of attribute. As shown below, the results between the first `str` and the second run are different. The second `str` overrode the type accordingly.
```{r Change of attribute type, echo=TRUE}
#check the type of each attribute and change to factor or int
str(df)

df$sex <- as.factor(df$sex)
df$cp <- as.factor(df$cp)
df$fbs <- as.factor(df$fbs)
df$restecg <- as.factor(df$restecg)
df$exang <- as.factor(df$exang)
df$slope <- as.factor(df$slope)
df$thal <- as.factor(df$thal)

str(df) #re-run
```
One of the most crucial steps in data analysis is dealing with the missing data. Usually, the complete dataset doesn't take place at the industry level. The code `missmap` is the perfect tool to visualize the missing data in each attribute. Luckily, the graph suggests that there isn't any missing data for this dataframe. 
```{r Missmap, echo=TRUE}
#check for any missing data
library(Amelia)
missmap(df, main = "Missing Data vs Observed")
```

The final step before analyzing the data is checking the ratio of the categories in the response variable. The resampling method can resolve the high imbalance between the classification. However, the below result provides that the imbalance isn't significant enough to apply under/over-sampling algorithm.
```{r Count each categorical value, echo=TRUE}
#check the ratio of reponse variable and see if it requires to rebalance
library(plyr)
count(df,vars="target")
```

## 3. Data Visualization

```{r Data Visualization Package,echo=TRUE}
#Data Visualization
library(GGally)
library(ggsci)
```

```{r Frequency of Target, echo=TRUE, fig.height=5, fig.width=4}
#1. Count of Target variable
ggplot(df, aes(factor(target), fill=factor(target)))+
  geom_bar(stat="count", width=0.5, color="black")+
  ggtitle("Count of Target")+xlab("Target")+ylab("Count")+labs(fill="Target")+
  theme_bw()+
  scale_fill_npg()
```

```{r Frequency of Gender broken by Target, echo=TRUE, fig.height=5, fig.width=6}
#2. Barplot of Gender broken down by Target
ggplot(df, aes(sex, fill=factor(target)))+
  geom_bar(stat="count", width=0.5, color="black", position=position_dodge())+
  ggtitle("Gender of Patient, Broken by Target")+xlab("Gender")+ylab("Count")+labs(fill="Target")+
  theme_bw()+
  scale_fill_npg()
```

```{r For Loop Barplot of Categorical Variables, echo=TRUE, fig.height=5, fig.width=6}
#3. Barplot for categorical variables broken down by Target
cat_var <- c("sex", "cp", "fbs", "restecg", "exang", "slope", "thal", "target")
cat_df <- df[cat_var]

for(i in 1:7){
  print(ggplot(cat_df, aes(x=cat_df[,i], fill=factor(target)))+
    geom_bar(stat="count", width=0.5, color="black", position=position_dodge())+
    ggtitle(paste(colnames(cat_df)[i], ": Broken by Target"))+
    xlab(colnames(cat_df)[i])+ylab("Count")+labs(fill="Target")+
    theme_bw()+
    scale_fill_npg())
}
```

```{r Boxplot of Age broken by Target, echo=TRUE}
library(ggpubr)
#4. Age distribution by Target
mp <- ggplot(df, aes(sex, age, fill=factor(target)))+
  geom_boxplot(width=0.5)+
  ggtitle("Distribution of Age, by Gender", subtitle="")+xlab("Gender")+ylab("Age")+labs(fill="Target")+
  theme_bw()+
  scale_fill_npg()
#4-1. subplots
xplot <- ggplot(df, aes(sex, fill=factor(target)))+
  geom_bar(stat="count", width=0.5, alpha=0.4,color="black", position=position_dodge())+
  labs(fill="Target")+
  theme_bw()+
  scale_fill_npg()
yplot <- ggplot(df, aes(age, fill=factor(target)))+
  geom_density(alpha=0.4)+
  labs(fill="Target")+
  theme_bw()+
  scale_fill_npg()+
  rotate()
#4-2. combination
library(ggpubr)
ggarrange(xplot, NULL, mp, yplot,
          ncol =2, nrow=2, align = "hv",
          widths= c(3,1), heights = c(1,2),
          common.legend= TRUE)
```

```{r For Loop Boxplot of Continuous Variables, echo=TRUE}
#5. Boxplot for continuous variables broken down by Target
cont_var <- c("age", "trestbps", "chol", "thalach", "oldpeak", "target")
cont_df <- df[cont_var]

for(i in 1:5){
  print(ggplot(cont_df, aes(x=cont_df[,i], y=factor(target), fill=factor(target)))+
          geom_boxplot(width=0.5)+
          geom_point(position=position_dodge(width=0.5), alpha=0.2)+
          ggtitle(paste(colnames(cont_df)[i], ": Broken by Target"))+
          xlab(colnames(cont_df)[i])+ylab("Target")+labs(fill="Target")+
          theme_bw()+
          scale_fill_npg())
}
```

## 4. Logistic Regression
At the beginning of this notebook, we studied the concept of logistic regression. Unlike the linear regression, the classification method applies accuracy, precision, F1 score, and related indicators to measure the validity. Splitting the entire data frame between the train and test sets is essential to avoid biased results. The `train_df` is used only to study and determine the appropriate model.
For this study, I split the data frame between the train and test sets with the ratio of 4:1. It is crucial to randomly allocate the incidences in the data sets. First, `set.seed` will randomize the incidences, followed by the division. Once the statistical model is discovered and validated, the same model will be used to predict the possible patient.
```{r Train-Test Split, echo=TRUE}
#Train,Test Split
library(caTools)
set.seed(1234)
sample <- sample.split(df, SplitRatio = 0.75) #Randomly set identifier
train_df <- subset(df, sample==TRUE) #Train dataset
test_df  <- subset(df, sample==FALSE) #Test dataset
```

#### 4-1. Fitting the model
Discovering the statistically significant variable is extremely difficult with the help of data visualization. The `train_df` is applied to the logistic regression. As our response variable consists of only two categories, the binomial distribution is chosen as the `family` in `glm`.
The summary of the first model indicates the AIC score of 171.97 with 197 degrees of freedom. The coefficient gives an insight into the full model of logistic regression. In the printed summary, the rightmost column is the P-value of each coefficient in the model. The more they are statistically significant, the more codes appear on the right side. 
```{r Fitting Train_df, echo=TRUE}
#Logistic Regression: full fitting with train dataset
df_model <- glm(target~., data=train_df, family=binomial(link="logit"))
exp(coef(df_model))
summary(df_model)
```
The result above indicates that the variables, `sex`, `cp`, `trestbps`, `thalach`, `oldpeak`, and `ca`, are statistically significant. I created `df_model.part` by fitting only listed variables. The summary below is the fitted model of only significant variables: the AIC score of 171.89 with the degrees of freedom of 206. The AIC difference between partial and complete model is -0.0749. The reduced model has a lower AIC score, which suggests that it is better fitted than the full model. The ANOVA test is conducted to prove the difference exists between the comprehensive and partial model.

```{r Fitting only significant variables, echo=TRUE}
#create a model with the statistically siginifcant variables only
df_model.part <- glm(target~sex+cp+trestbps+thalach+oldpeak+ca, data=train_df, family=binomial(link="logit"))
exp(coef(df_model.part))
summary(df_model.part)
print(df_model.part$aic - df_model$aic) #difference of AIC score
```
The ANOVA test is used to compare the difference between the two statistical figures. The Chi-Square test helps determine whether the `df_model.part` differs significantly from the `df_model`. The p-value of the test is the key to decide between the rejection of the Null Hypothesis. The lower the p-value, the evidence of difference is, hence confidently reject the null hypothesis. The p-value is compared with the significance value to make the decision. 

* H_0: `df_model.part` = `df_model`
* H_A: `df_model.part` ≠ `df_model`

The test result shows a p-value of 0.02496 which, is lower compare to 0.05. Based on this result, we can reject the null and select the alternative hypothesis. The prediction steps will use the `df_model.part` as it is proved that the reduced model is statistically more fit.
```{r ANOVA test for two diffent models, echo=TRUE}
#validate that the reduced model is statistically siginifcant over the full model
anova(df_model.part, df_model, test="Chisq")
```
#### 4-2. Predictability and Performance Evaluation

The previous step was to fit, check and discover the appropriate regression model. The final step of the logistic regression analysis is to apply the model to `test_df` and test the predictability. The two most commonly used technics are Confusion Matrix and Receiver Operating Characteristic Curve.
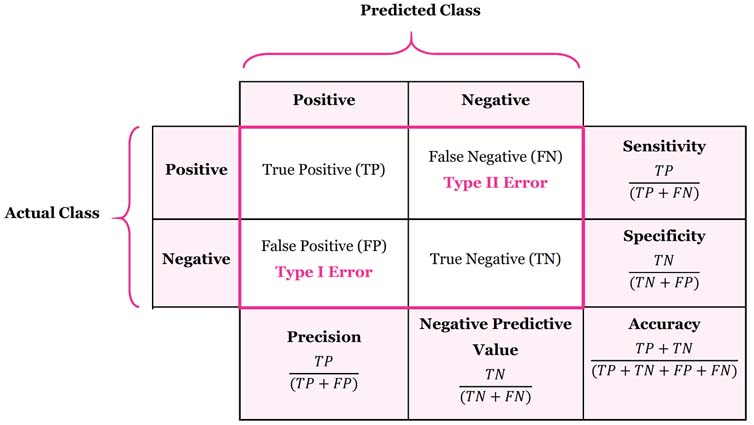
A confusion matrix is a table used to describe the performance of a classification model. A table layout helps to exhibit the performance of the model. It contains two dimensions, 'actual' and 'predicted', and the cells are determined by the number of categories in a response variable. It is an excellent tool to present the accuracy of a model, Type I and Type II errors. The insight and calculations are presented in the image below.

![Confusion Matrix](https://2.bp.blogspot.com/-EvSXDotTOwc/XMfeOGZ-CVI/AAAAAAAAEiE/oePFfvhfOQM11dgRn9FkPxlegCXbgOF4QCLcBGAs/s1600/confusionMatrxiUpdated.jpg)

Another measure of predictability of the model is Receiver Operating Characteristic(ROC) curve and Area Under the Curve (AUC) Score. The ROC measures the performance of a classification model. The plot represents the trade-off between True Positive Rate (also known as Sensitivity) versus False Positive Rate (1-Specificity). As the name of AUC suggests, it is derived from the plot by calculating the area below the curve. Higher the AUC, better predictability of the fitted model. 

![ROC Curve](https://ars.els-cdn.com/content/image/3-s2.0-B9780128030141000029-f02-01-9780128030141.jpg)

The below curve is the sample of the ROC Curve with the AUC of the fitted model versus the actual data. It is not crucial to derive the curve and score of the fitted model. As the curve is based on predictability, it is wise to use the technic to the `test_df`.
```{r ROC and AUC partial model, echo=TRUE}
#ROC and AUC for the partial model
library(pROC)
par(pty="s")
roc(train_df$target, df_model.part$fitted.values, plot=TRUE, legacy.axes=TRUE,
    col="Red", print.auc = TRUE, print.auc.x=0.35,
    xlab="False Positive Rate",
    ylab="True Positive Rate")
```

Using the reduced model, we can predict the heart disease `target` for the `test_df`. The code produces predicted values. The prediction is then compared with the actual `target` from the test dataframe. 
Based on the summary of Confusion Matrix, a total of 67 sample patients were accurately predicted. Out of 19 false predictions, 8 are Type I error and, 11 are Type II errors. Even though eight patients didn't have heart disease, they are falsely diagnosed. Eleven patients have heart disease but are predicted to be none. The accuracy of the model is 77.91% with a confidence interval of (67.67%, 86.14%). The p-value of accuracy is lower than 0.05, which indicates that the confusion matrix is statistically significant. 
```{r Confusion Matrix, echo=TRUE}
#Fiiting the model to test dataset and Confusion Matrix of the fitted model
df_model_fit <- predict(df_model.part, newdata=test_df, type="response")
df_model_confmat <- ifelse(df_model_fit >0.5, 1, 0)

library(caret)
confusionMatrix(factor(df_model_confmat), factor(test_df$target), positive=as.character(1))
```
Another way to measure the predictability of the model is by deriving the ROC curve and AUC score. The graph is clearly above the diagonal line. It is also close to the blue line. Hence it can be considered as an accurate model. AUC score for the curve is 0.8696, which is very close to 1. As the maximum value of AUC is 1 (which is the perfect prediction), the prediction is achieved accurately. 
```{r ROC and AUC of Fitted Model, echo=TRUE, fig.height=6, fig.width=6}
#ROC and AUC for the fitted model
library(ROCR)
df_prediction <- prediction(df_model_fit, test_df$target)
df_performance <- performance(df_prediction, measure = "tpr", x.measure="fpr")
plot(df_performance, col = "Red", 
     main = "ROC Curve",
     xlab="False Postiive Rate", ylab="True Positive Rate")+ 
  abline(v=0, h=1, col="Blue", lty=2)+
  abline(a=0, b=1, col= "Grey", lty=3)+
  plot(df_performance, col = "Red", 
     main = "ROC Curve",
     xlab="False Postiive Rate", ylab="True Positive Rate", add=TRUE)


df_auc <- performance(df_prediction, measure = "auc")
df_auc <- df_auc@y.values
print(paste("AUC: ", lapply(df_auc,round,4)))
```

## 5. Conclusion
The logistic regression initially started with the importation of the data from the local device. The dataframe didn't contain any missing data hence not many of cleansing technique was required. However, the type of every attribute is characterized as an integer. To successfully conduct the classification, I changed categorical variables into type factors. The completion of cleansing led to data visualization.

The most crucial step of this study was discovering the regression model and predict patients. First, I split `train` and `test` data sets from the complete dataframe. Of course, the division of incidences was conducted at random. 
Initially, the regression was fit only by the `train_df`. The summary of the fit suggested that `sex`, `cp`, `trestbps`, `thalach`, `oldpeak` and `ca` are statistically significant. The model was then chosen only significant variables and fitted again. The formula of the regression was:

* **target** = 0.4415 + 0.1261[**sex1**] + 5.6280[**cp1**] + 8.9356[**cp2**] + 13.1413[**cp3**] + 0.9775[**trestbps**] + 1.0386[**thalach**] + 0.4781[**oldpeak**] + 0.3140[**ca**]

The AIC score difference between full and partial model was **-0.07491**. The reduced model produced better result. The ANOVA test follwed to statistically prove that the reduced model was better fit. With the p-value of **0.02496**, I could conclude that the reduced model outperformed the full model.
The main goal of the study was to predict the heart disease of the patient. I used the two most well-known techniques to check the predictability of the fitted model: the confusion matrix and the ROC curve. The accuracy of the prediction was **77.91%**: out of 86 sample sizes, 67 were predicted correctly. The shape of the ROC curve was close to the blue line with an AUC score of **0.8696**. These results confirm that the predictability of the model is statistically accurate.