README.md

1594. Maximum Non Negative Product in a Matrix

You are given a m x n matrix grid. Initially, you are located at the top-left corner (0, 0), and in each step, you can only move right or down in the matrix.

Among all possible paths starting from the top-left corner (0, 0) and ending in the bottom-right corner (m - 1, n - 1), find the path with the maximum non-negative product. The product of a path is the product of all integers in the grid cells visited along the path.

Return the maximum non-negative product modulo 109 + 7. If the maximum product is negative, return -1.

Notice that the modulo is performed after getting the maximum product.

Example 1:

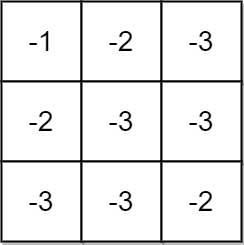
Input: grid = [[-1,-2,-3],[-2,-3,-3],[-3,-3,-2]]
Output: -1
Explanation: It is not possible to get non-negative product in the path from (0, 0) to (2, 2), so return -1.

Example 2:

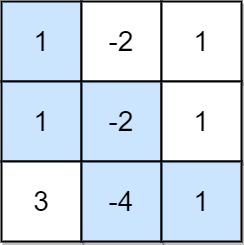
Input: grid = [[1,-2,1],[1,-2,1],[3,-4,1]]
Output: 8
Explanation: Maximum non-negative product is shown (1 * 1 * -2 * -4 * 1 = 8).

Example 3:

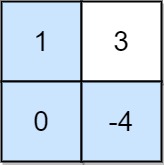
Input: grid = [[1,3],[0,-4]]
Output: 0
Explanation: Maximum non-negative product is shown (1 * 0 * -4 = 0).

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 15
• -4 <= grid[i][j] <= 4

Solutions (Rust)

1. Solution

impl Solution {
    pub fn max_product_path(grid: Vec<Vec<i32>>) -> i32 {
        let m = grid.len();
        let n = grid[0].len();
        let mut products = vec![vec![[1, -1]; n]; m];
        products[0][0] = [grid[0][0].min(1) as i64, grid[0][0].max(-1) as i64];

        for i in 0..m {
            for j in 0..n {
                if i + 1 < m {
                    if grid[i + 1][j] > 0 {
                        products[i + 1][j][0] =
                            products[i + 1][j][0].min(products[i][j][0] * grid[i + 1][j] as i64);
                        products[i + 1][j][1] =
                            products[i + 1][j][1].max(products[i][j][1] * grid[i + 1][j] as i64);
                    } else if grid[i + 1][j] < 0 {
                        products[i + 1][j][0] =
                            products[i + 1][j][0].min(products[i][j][1] * grid[i + 1][j] as i64);
                        products[i + 1][j][1] =
                            products[i + 1][j][1].max(products[i][j][0] * grid[i + 1][j] as i64);
                    } else {
                        products[i + 1][j] = [0, 0];
                    }
                }
                if j + 1 < n {
                    if grid[i][j + 1] > 0 {
                        products[i][j + 1][0] =
                            products[i][j + 1][0].min(products[i][j][0] * grid[i][j + 1] as i64);
                        products[i][j + 1][1] =
                            products[i][j + 1][1].max(products[i][j][1] * grid[i][j + 1] as i64);
                    } else if grid[i][j + 1] < 0 {
                        products[i][j + 1][0] =
                            products[i][j + 1][0].min(products[i][j][1] * grid[i][j + 1] as i64);
                        products[i][j + 1][1] =
                            products[i][j + 1][1].max(products[i][j][0] * grid[i][j + 1] as i64);
                    } else {
                        products[i][j + 1] = [0, 0];
                    }
                }
            }
        }

        (products[m - 1][n - 1][1] % 1_000_000_007) as i32
    }
}