Skip to content

Latest commit

 

History

History
146 lines (80 loc) · 4.92 KB

B-Tree.md

File metadata and controls

146 lines (80 loc) · 4.92 KB
Raw

B-Tree



1) 정의

B-tree는 이진트리의 확장된 개념으로 하나의 노드가 가질 수 있는 자식 노드가 2개 이상인 트리를 말합니다. B-tree는 방대한 양의 데이터를 저장하고 관리하는 곳에 주로 쓰이며 데이터베이스와 파일 시스템에 사용됩니다.





2) 노드의 구조와 특징


노드의 구조

  • k개의 키 : 오름차순으로 정렬되어있음
  • k+1개의 포인터
    • 왼쪽 : 해당 키 값보다 작은 키들이 있는 자식노드
    • 오른쪽 : 해당 키 값보다 큰 키들이 있는 자식노드

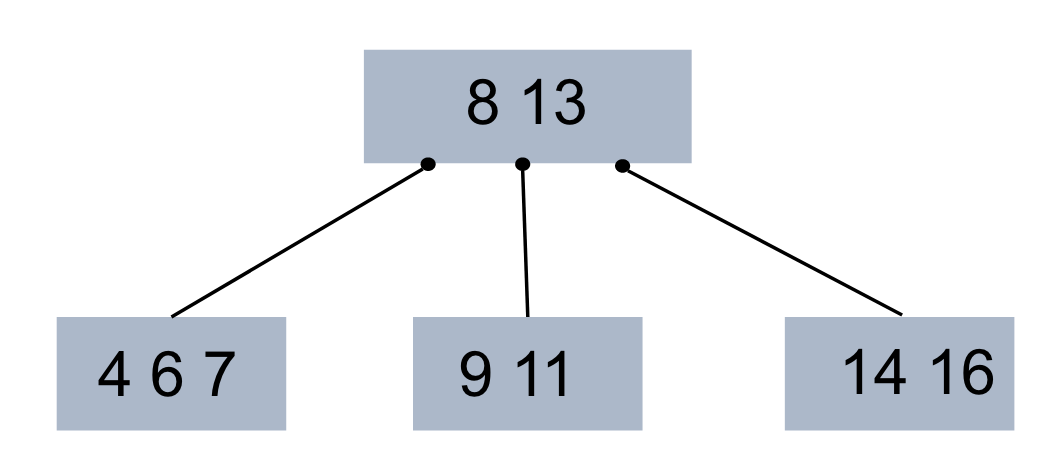
특징1) 차수 : 노드가 최대로 가질 수 있는 key개수
ex)그림은 3차 B트리

특징2) 균형을 이뤄야한다(Balanced Tree) = 모든 리프노드로까지의 길이가 같아야한다

특징3) 중복된 값을 입력할 수 없다





3) key검색

: 균형트리이기때문에 어떤 키도 O(logN)안에 탐색에 가능하며, 이진트리와 다르게 자식노드를 여러개 갖기 때문에 레벨이 낮아 훨씬 빨리 탐색가능

알고리즘

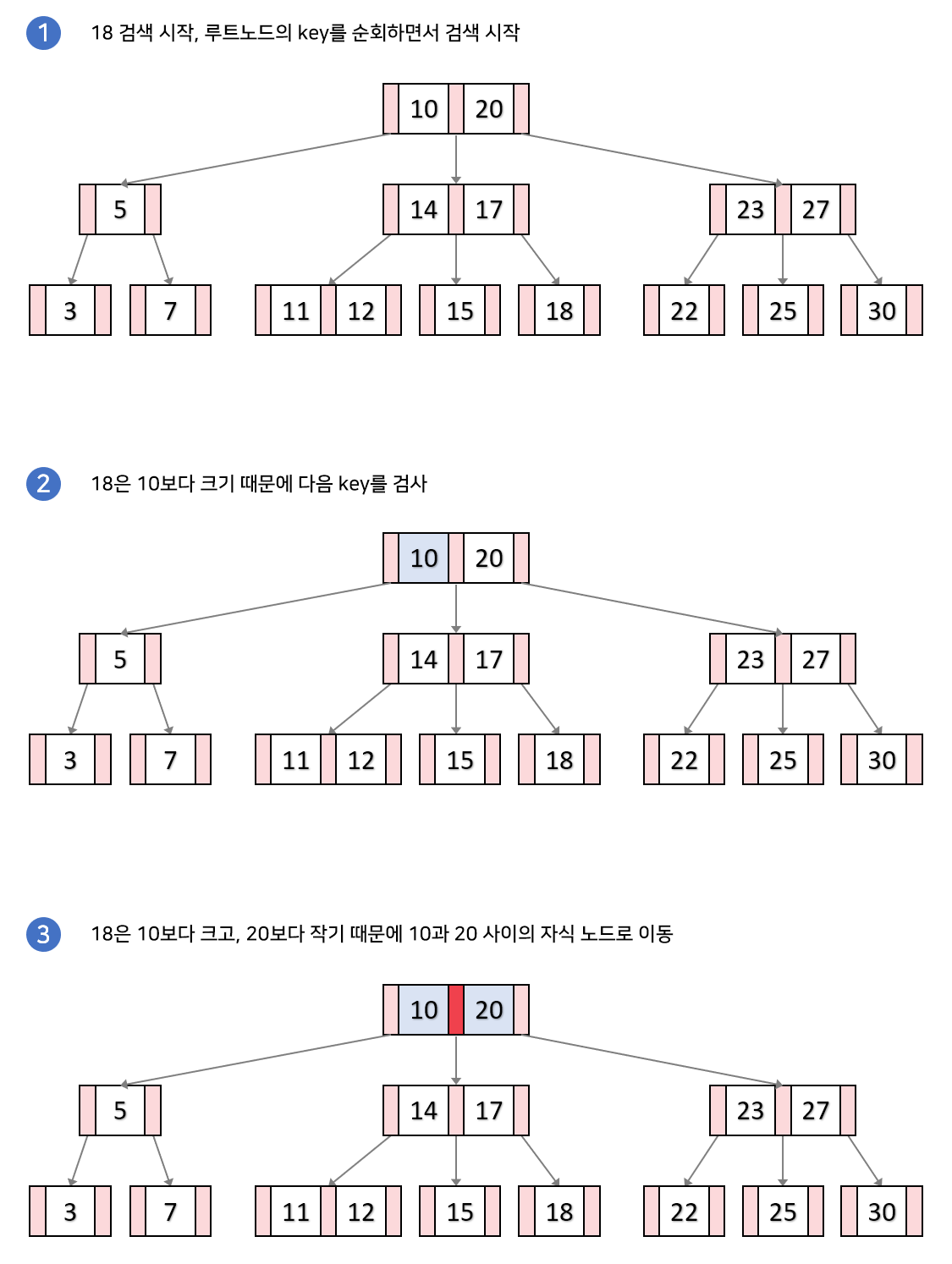
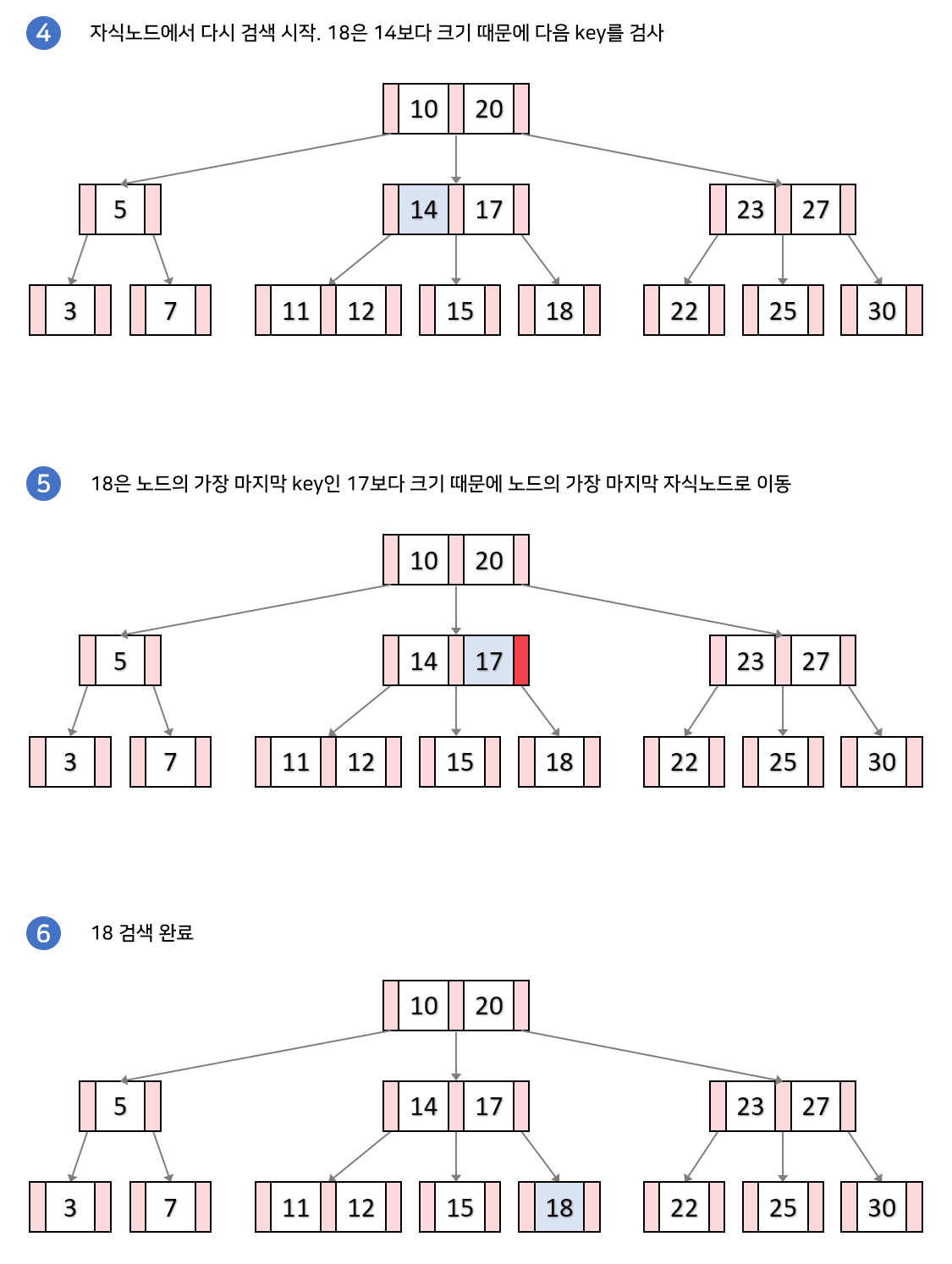
  • 루트노드부터 시작

    • 노드에 있는 키와 순차적으로 대소비교를 통해 포인터를 선택
    • 찾는 값과 같은 키 발견하면 종료

  • 리프노드까지 반복, 끝까지 찾지못한다면 탐색실패







4) key삽입

알고리즘

  • 아무것도 없을 때 : 루트노드만들고 key삽입
  • 루트노드만 있을 때
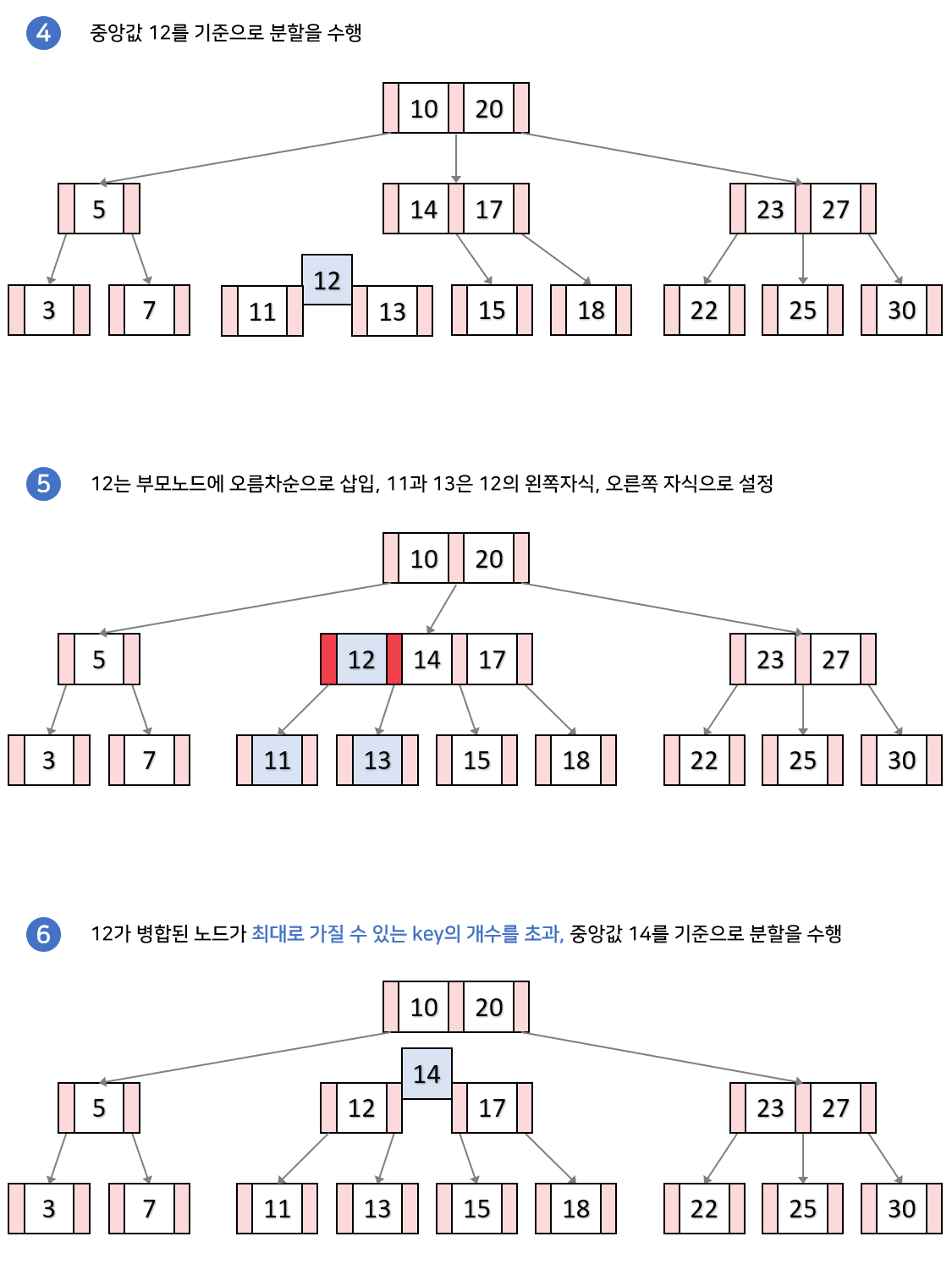
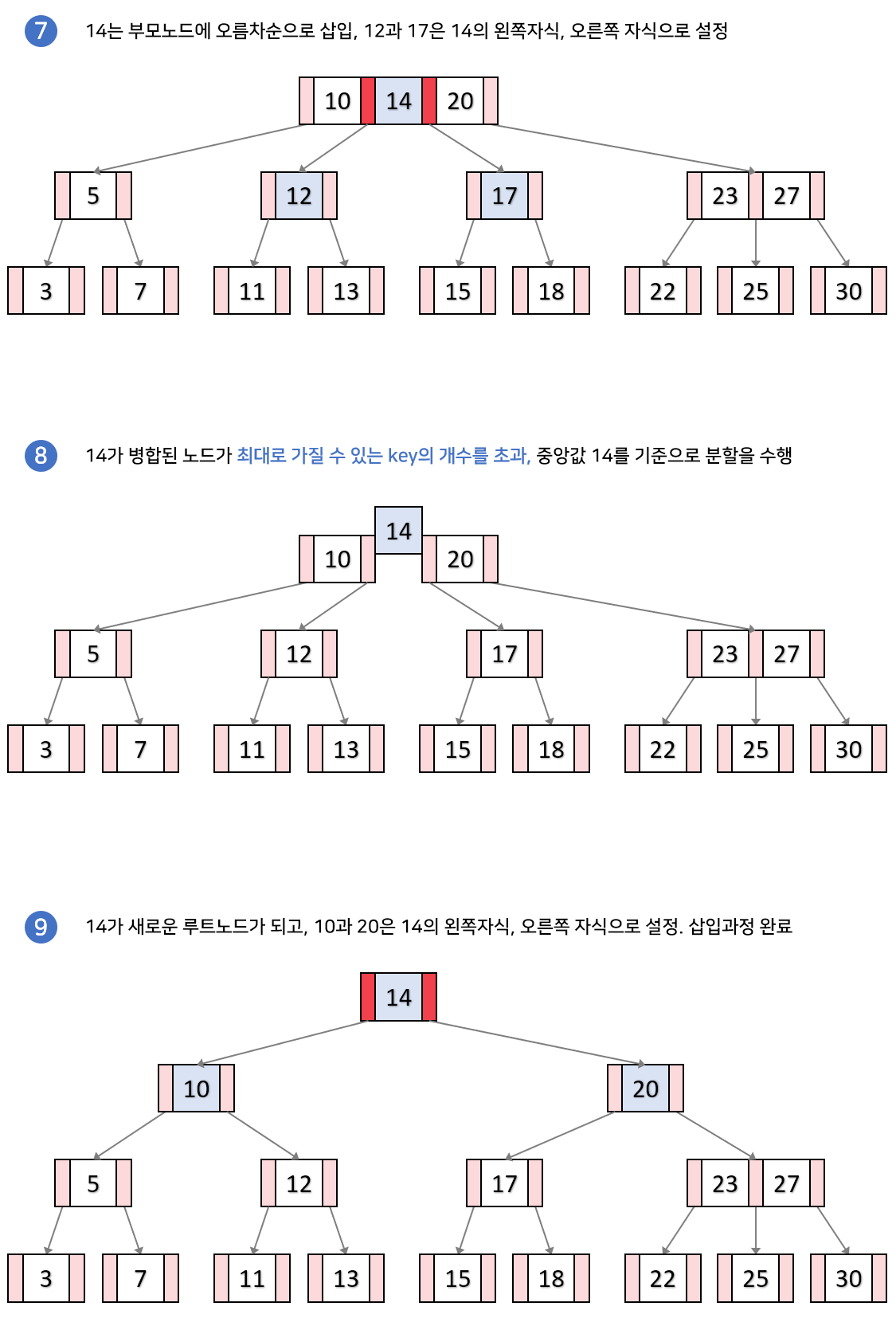
    • 꽉 찼을 때: 루트노드에 넣고 중간키를 노드로 만들어서 위로 올린뒤 중간보다 작은값들을 왼쪽노드로 중간보다 큰 값들을 오른쪽 노드로 분할한다.
    • 자리 있을 때: 오름차순으로 키 값 삽입
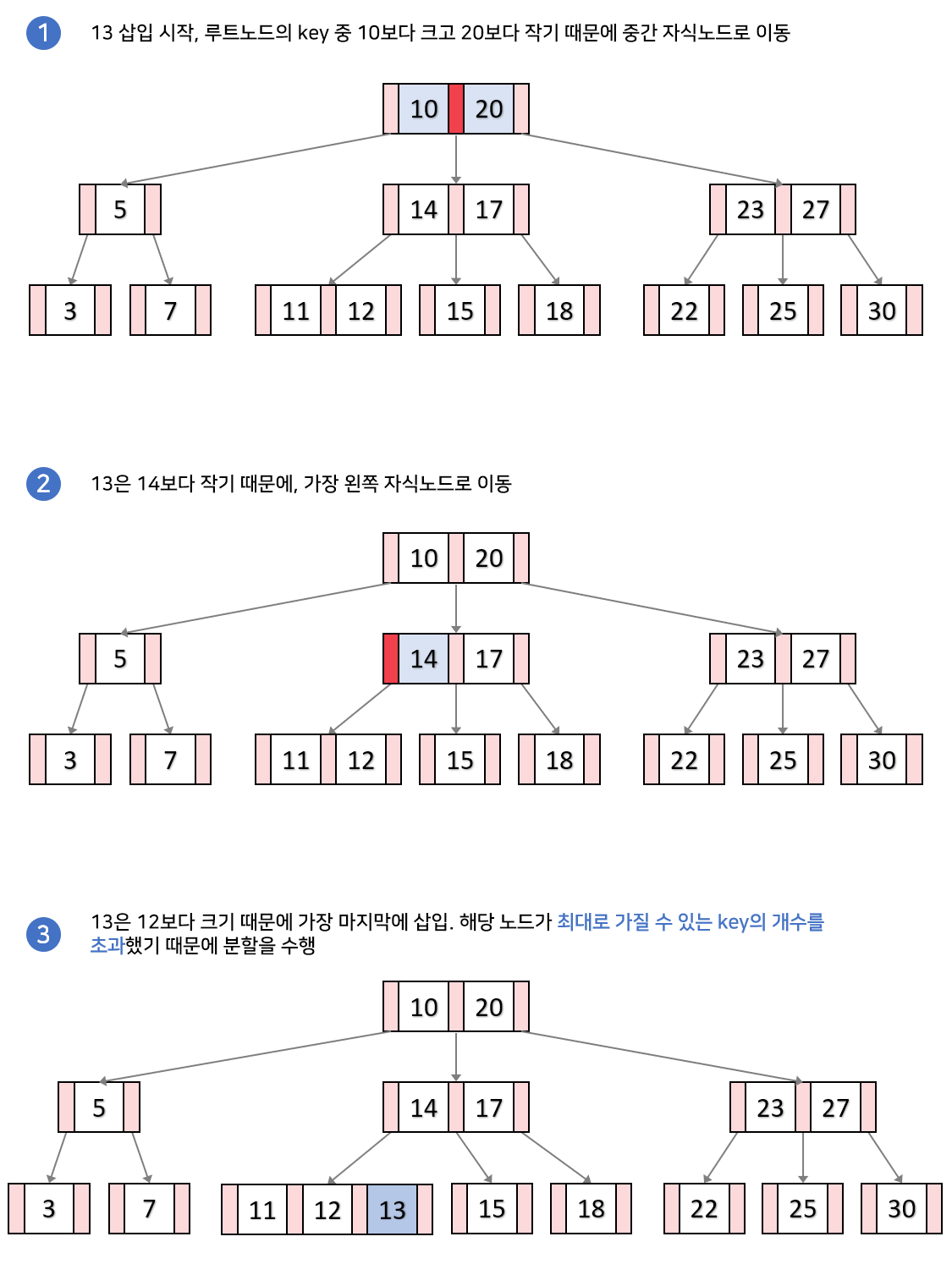
  • 여러 노드들 있을 때: 비교를 통해 삽입 값이 들어갈 적합한 리프노드까지 내려간다
    • 리프노드 꽉 찼을 때: 리프노드에 넣고 중간키를 부모노드로 올리고 포인터를 알맞게 매치해준다 *
    • 리프노드 자리 있을 때: 오름차순으로 키 값 삽입



*인 경우




5) key삭제

알고리즘

  • 삭제할 키가 리프에 있는 경우

    • 노드에 최소 키 이상있는 경우 : 삭제
    • 노드가 최소 키인 경우
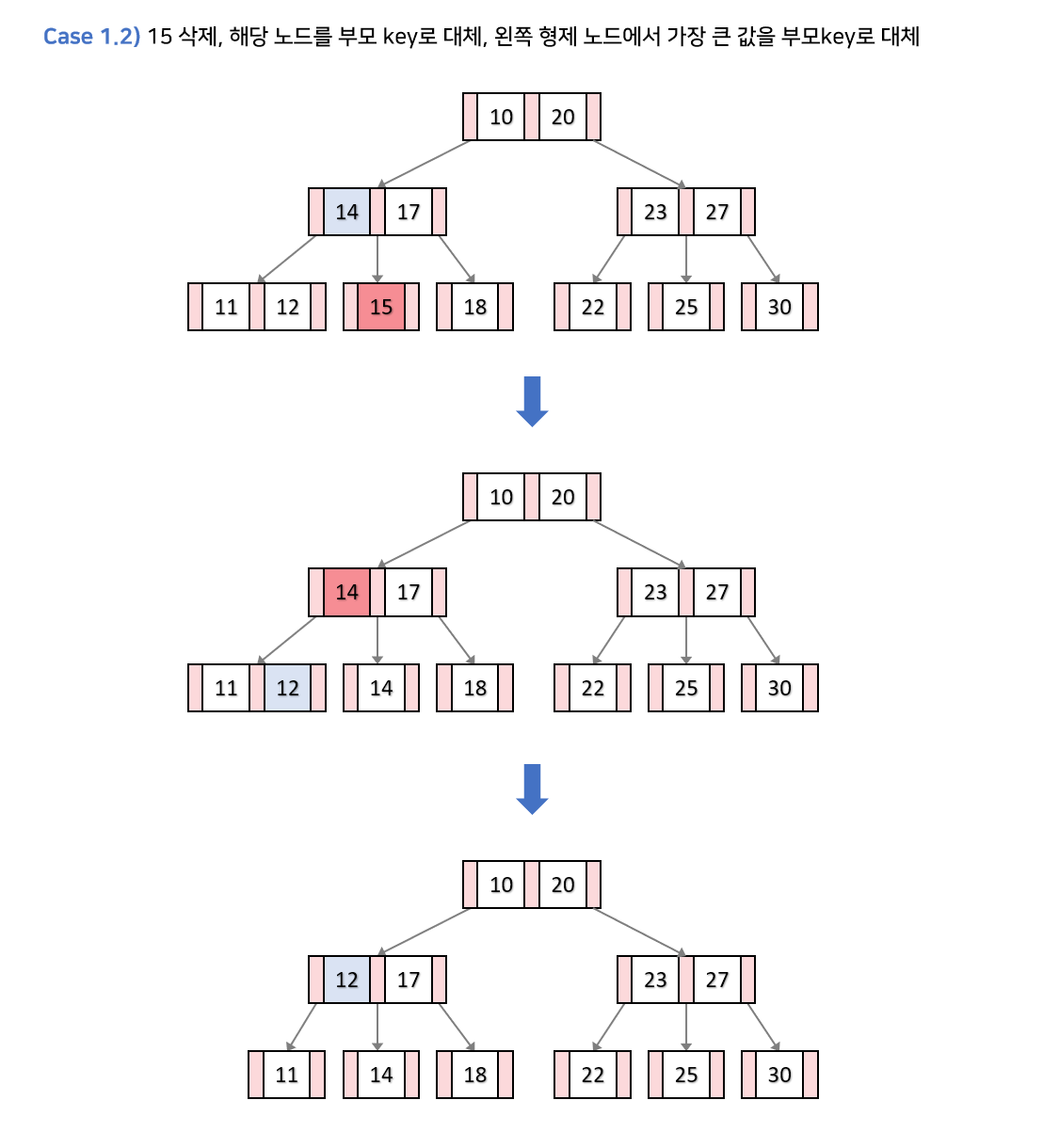
      • 형제노드가 최소가 키가 아닌 경우 : 삭제 후 부모키를 내리고 부모키자리에 적절한 형제 노드의 키를 올린다 (1)
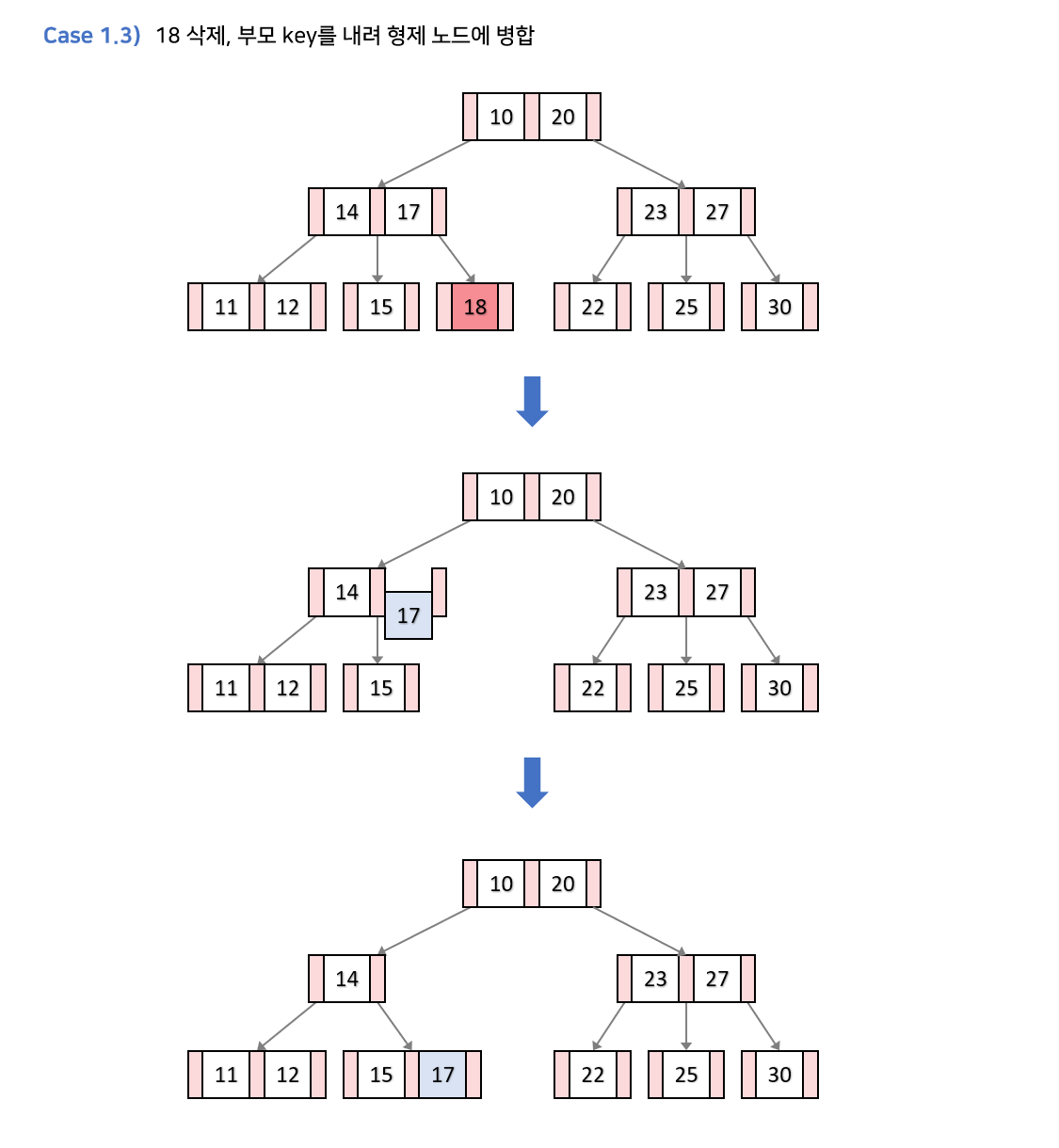
      • 형제노드가 모두 최소 키인 경우 : 삭제 후 부모키와 형제노드 병합 (2)



(1)



(2)





알골리즘

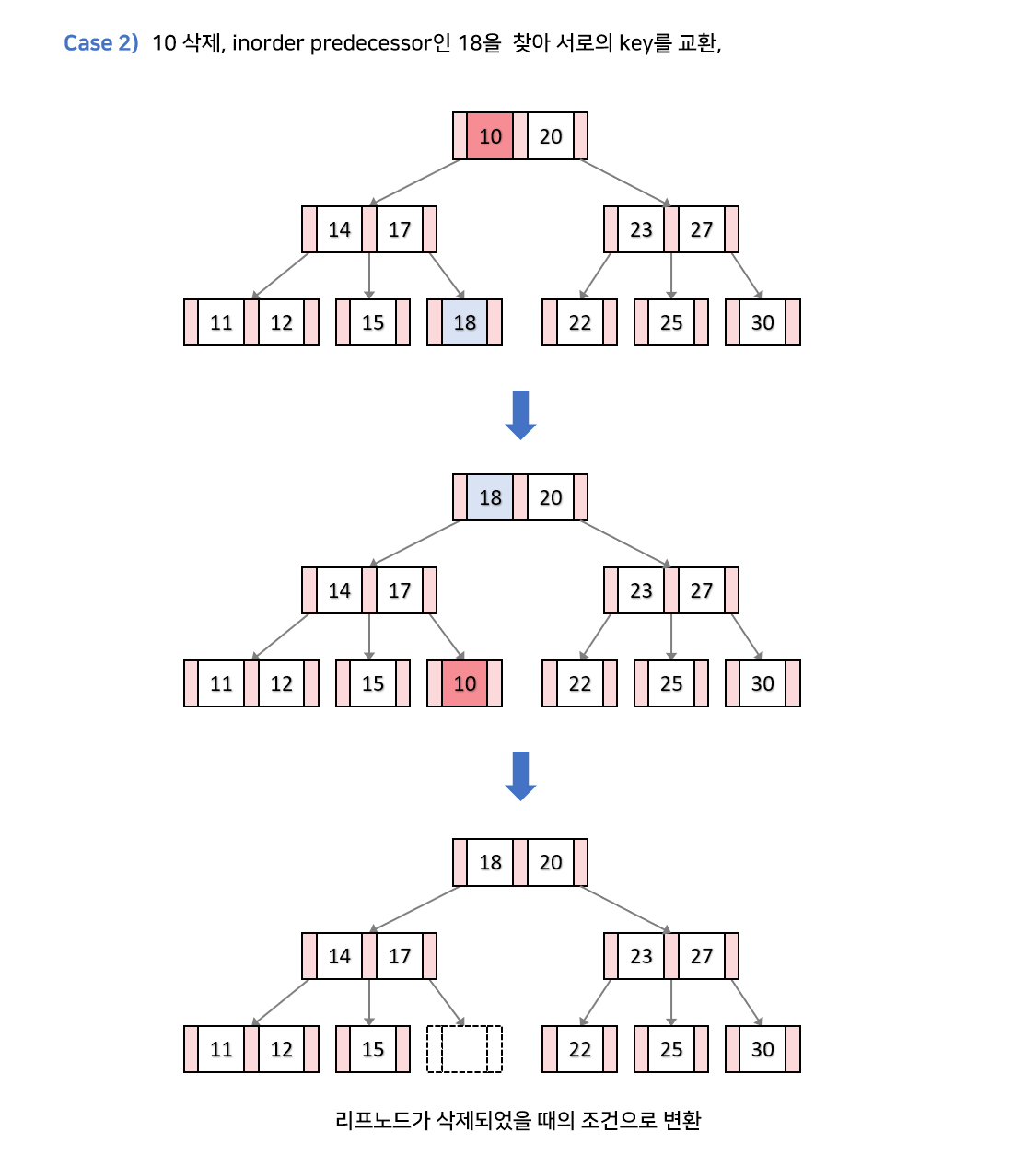
  • 삭제할 키가 내부노드에 있는 경우
    • 노드나 자식노드의 키 수가 최소 키보다 많을 경우 : 자식 중 가장큰값(or 가장작은값)과 교환 후 삭제 -> 리프노드삭제로 변환 (3)
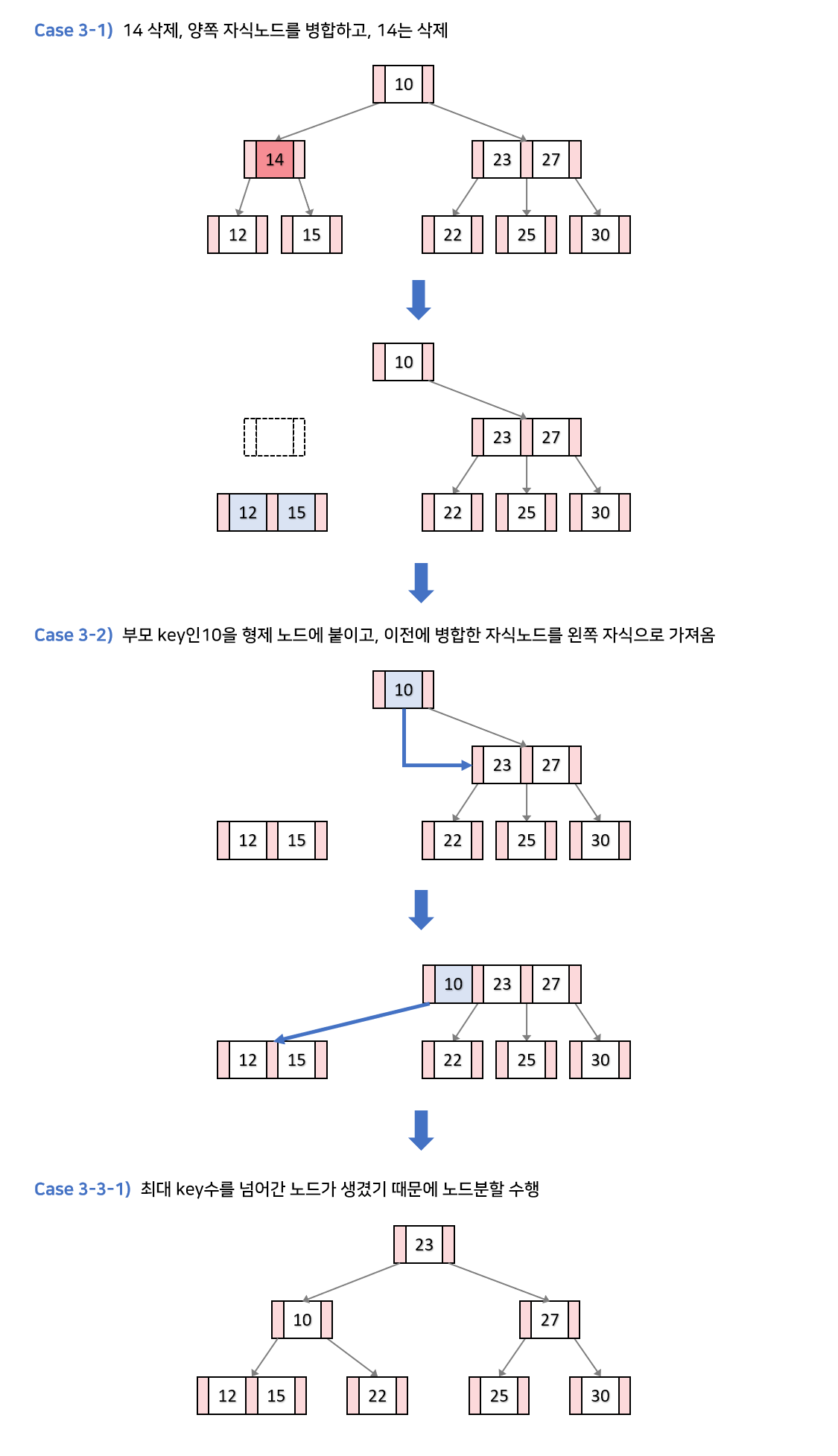
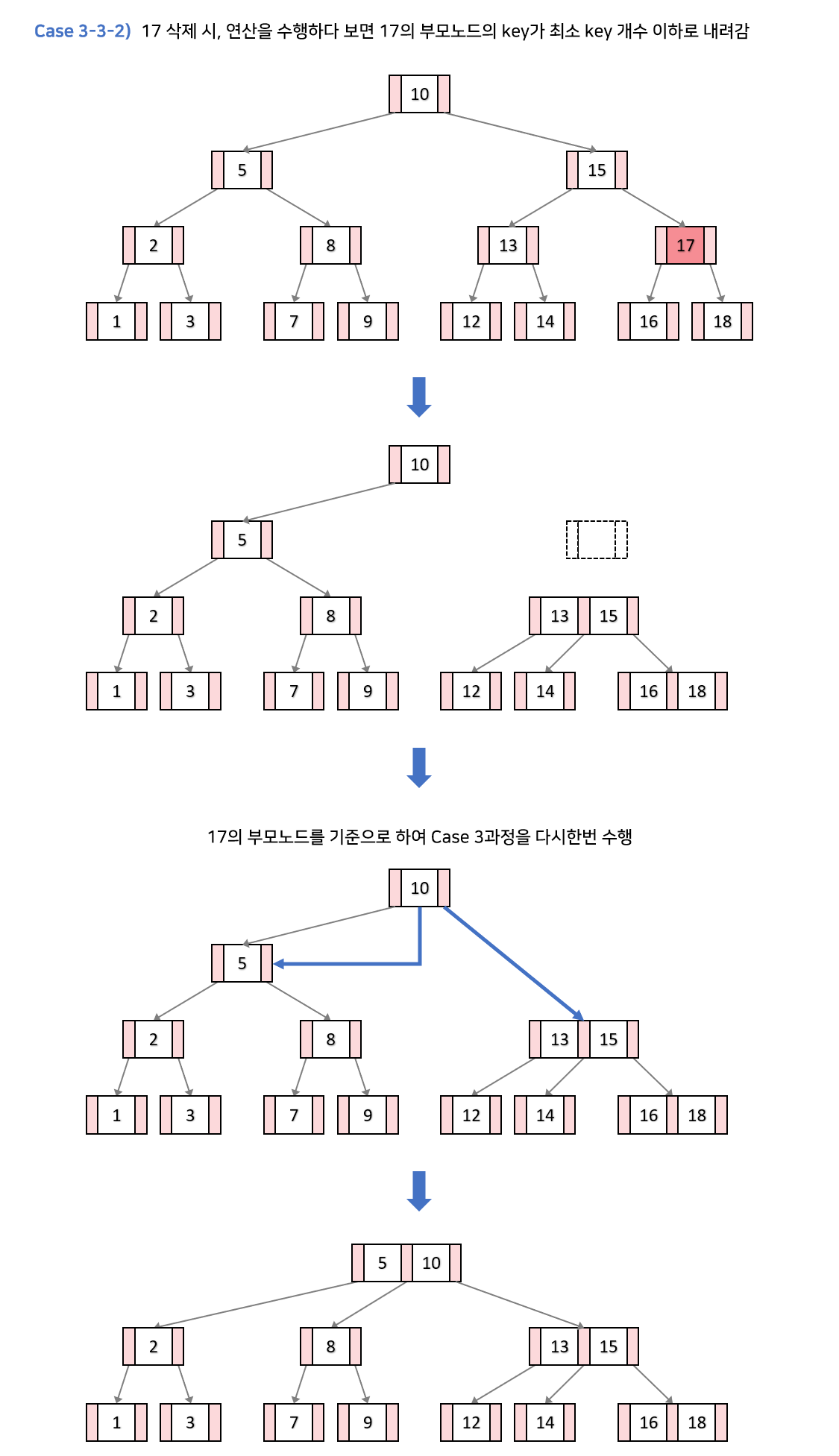
    • 노드나 자식노드의 키 수가 최소 키일경우 : 삭제 후 자식노드를 합치고 부모키도 인접 자식키와 합칩니다. 그뒤에 그 부모키의 자식노드를 합친 자식노드들로 갖게 합니다. (4)

(3)



(4-1) 최대키수 넘는 경우 : 재분배



(4-2) 균형이 망가지는 경우 : 병합





참고