Consider matrix addition. Can one use shared memory to reduce the global memory bandwidth consumption? Hint: Analyze the elements accessed by each thread and see if there is any commonality between threads.
No, it can't. The thread which computes Output(i, j) only needs Input_1(i,j) and Input_2(i, j). No input element is shared by multiple threads.
Draw the equivalent of Fig. 4.14 for an 8× 8 matrix multiplication with 2× 2 tiling and 4× 4 tiling. Verify that the reduction in global memory bandwidth is indeed proportional to the dimensions of the tiles.
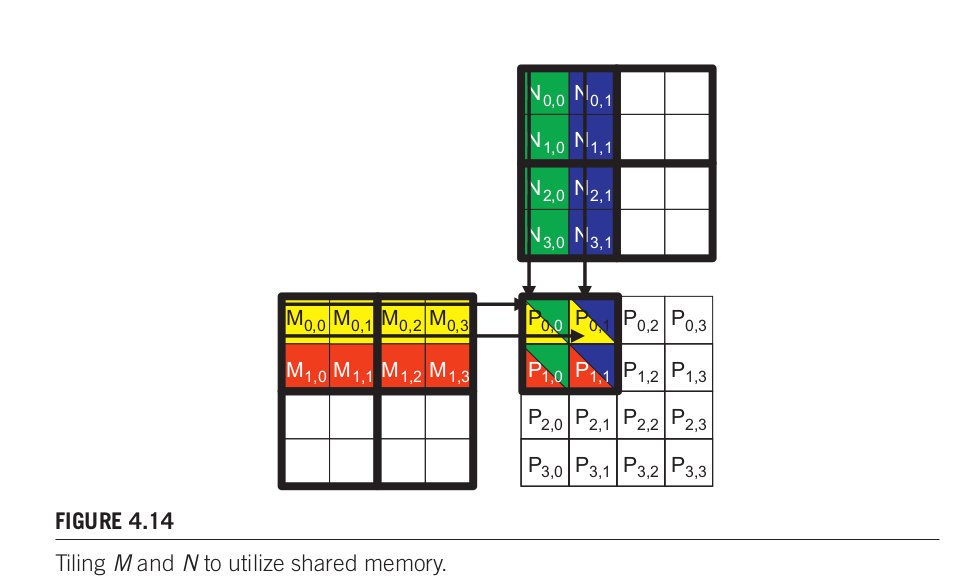
Dimension of inputs and output: 8*8 times 8*8 -> 8*8
If using 2*2 tile, the total number of tiles is 16. For each tile, the total number of global memory access is 2*(2*8).
If using 4*4 tile, the total number of tiles is 4. For each tile, the total number of global memory access is 2*(4*8) .
If the input and output are (n,n) square matrix and tile size is (t, t), there are tiles in total. The number of global memory access in a tile is
. The total number of global memory access is
.
The result shows that the global memory accesses decreases with bigger tile size. Using bigger tiles could accelerate matrix multiplication, but is needs bigger shared memory.
What type of incorrect execution behavior can happen if one or both __syncthreads() are omitted in the kernel of Fig. 4.16?

A thread may access a location in shared memory when data is not ready.
Assuming that capacity is not an issue for registers or shared memory, give one important reason why it would be valuable to use shared memory instead of registers to hold values fetched from global memory? Explain your answer.
Shared memory is shared between threads in a block. There are common conditions where multiple thread read the same data, which only need to be fetched and stored once in shared memory.
For our tiled matrix–matrix multiplication kernel, if we use a 32x32 tile, what is the reduction of memory bandwidth usage for input matrices M and N? A. 1/8 of the original usage B. 1/16 of the original usage C. 1/32 of the original usage D. 1/64 of the original usage
C. According to Exercise 4.2, the number of shared memory access after tiling is , which is originally
. The reduction is 1/32.
In the previous question, if a variable is declared as a shared memory variable, how many versions of the variable will be created throughout the lifetime of the execution of the kernel?
D. Local variable belongs to a particular thread.
In the previous question, if a variable is declared as a shared memory variable, how many versions of the variable will be created throughout the lifetime of the execution of the kernel?
C. Shared memory belongs to a block.
Consider performing a matrix multiplication of two input matrices with dimensions N × N. How many times is each element in the input matrices requested from global memory in the following situations? A. There is no tiling. B. Tiles of size T × T are used.
A: N.
B: N/T
A kernel performs 36 floating-point operations and 7 32-bit word global memory accesses per thread. For each of the following device properties, indicate whether this kernel is compute- or memory-bound. A. Peak FLOPS= 200 GFLOPS, Peak Memory Bandwidth= 100 GB/s B. Peak FLOPS= 300 GFLOPS, Peak Memory Bandwidth= 250 GB/s
Actual computation memory access ratio = 36/(7*4 Byte) = 1.28
A: Peak computation memory access ratio = 200/100 = 2 > 1.28. Memory bound
B: Peak computation memory access ratio = 300/250 = 1.2< 1.28. Compute bound
To manipulate tiles, a new CUDA programmer has written the following device kernel, which will transpose each tile in a matrix. The tiles are of size
BLOCK_WIDTHbyBLOCK_WIDTH, and each of the dimensions of matrix A is known to be a multiple of BLOCK_WIDTH . The kernel invocation and code are shown below.BLOCK_WIDTHis known at compile time, but could be set anywhere from 1 to 20.dim3 blockDim(BLOCK_WIDTH,BLOCK_WIDTH); dim3 gridDim(A_width/blockDim.x,A_height/blockDim.y); BlockTranspose<<<gridDim, blockDim>>>(A, A_width, A_height); __global__ void BlockTranspose(float* A_elements, int A_width, int A_height) { __shared__ float blockA[BLOCK_WIDTH][BLOCK_WIDTH]; int baseIdx=blockIdx.x * BLOCK_SIZE + threadIdx.x; baseIdx += (blockIdx.y * BLOCK_SIZE + threadIdx.y) * A_width; blockA[threadIdx.y][threadIdx.x]=A_elements[baseIdx]; A_elements[baseIdx]=blockA[threadIdx.x][threadIdx.y]; }A. Out of the possible range of values for
BLOCK_SIZE, for what values ofBLOCK_SIZEwill this kernel function execute correctly on the device? B. If the code does not execute correctly for allBLOCK_SIZEvalues, suggest a fix to the code to make it work for allBLOCK_SIZEvalues.
A: Only if BLOCK_SIZE=1 could the kernels execute correctly.
B:
dim3 blockDim(BLOCK_WIDTH,BLOCK_WIDTH);
dim3 gridDim(A_width/blockDim.x,A_height/blockDim.y);
BlockTranspose<<<gridDim, blockDim>>>(A, A_width, A_height);
__global__ void BlockTranspose(float* A_elements, int A_width, int A_height)
{
__shared__ float blockA[BLOCK_WIDTH][BLOCK_WIDTH];
int baseIdx=blockIdx.x * BLOCK_SIZE + threadIdx.x;
baseIdx += (blockIdx.y * BLOCK_SIZE + threadIdx.y) * A_width;
blockA[threadIdx.y][threadIdx.x]=A_elements[baseIdx];
__syncthreads(); // added
A_elements[baseIdx]=blockA[threadIdx.x][threadIdx.y];
}
