고정 소수점 & 부동 소수점.md

고정 소수점 & 부동 소수점

컴퓨터에서 실수를 표현하는 방법은 고정 소수점과 부동 소수점 두가지 방식이 존재한다.

1. 고정 소수점(Fixed Point)

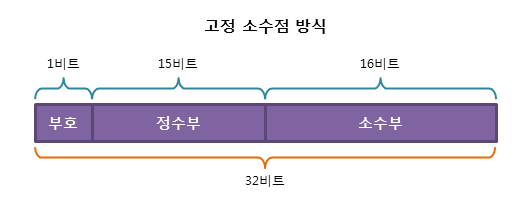
   소수점이 찍힐 위치를 미리 정해놓고 소수를 표현하는 방식 (정수 + 소수)

   -3.141592는 부호(-)와 정수부(3), 소수부(0.141592) 3가지 요소 필요함
   

   

   장점 : 실수를 정수부와 소수부로 표현하여 단순하다.

   단점 : 표현의 범위가 너무 적어서 활용하기 힘들다. (정수부는 15bit, 소수부는 16bit)

   
   
   

2. 부동 소수점(Floating Point)

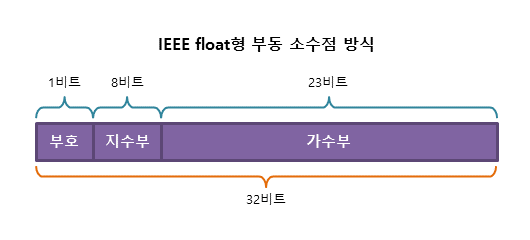
   실수를 가수부 + 지수부로 표현한다.

   • 가수 : 실수의 실제값 표현
   • 지수 : 크기를 표현함. 가수의 어디쯤에 소수점이 있는지 나타냄

   지수의 값에 따라 소수점이 움직이는 방식을 활용한 실수 표현 방법이다.

   즉, 소수점의 위치가 고정되어 있지 않는다.

   

   장점 : 표현할 수 있는 수의 범위가 넓어진다. (현재 대부분 시스템에서 활용 중)

   단점 : 오차가 발생할 수 있다. (부동소수점으로 표현할 수 있는 방법이 매우 다양함)

   
   
   

3. 고정 소수점과 부동 소수점의 일반적인 사용 사례.

고정 소수점 사용 상황.

1. 임베디드 시스켐과 마이크로컨트롤러

   • 메모리와 처리 능력이 제한된 환경에서 고정 소수점 연산이 일반적입니다. 이는 부동 소수점 연산을 지원하는 하드웨어가 없거나, 그러한 연산이 배터리 수명이나 다른 자원을 과도하게 소모할 수 있기 때문입니다.

2. 실시간 시스템

   • 예측 가능한 실행 시간이 중요한 실시간 응용 프로그램에서는 고정 소수점 연산이 선호됩니다. 이는 부동 소수점 연산이 가변적인 실행 시간을 가질 수 있기 때문입니다.

3. 비용 민감형 하드웨어

   • 부동 소수점 연산자를 지원하는 비용이 더 들 수 있어, 가격을 낮추기 위해 고정 소수점 연산을 사용하는 경우가 있습니다.

4. 디지털 신호 처리(DSP)

   • 일부 디지털 신호 처리 알고리즘은 정확하게 정의된 범위 내의 값을 사용하기 때문에 고정 소수점 연산으로 충분한 경우가 많습니다.

부동 소수점 사용 상황.

1. 과학적 계산

   • 넓은 범위의 값과 높은 정밀도가 요구되는 과학적 및 엔지니어링 계산에는 부동 소수점이 사용됩니다.

2. 3D 그래픽스

   • 3D 모델링과 같은 그래픽 작업에서는 부동 소수점 연산이 광범위하게 사용되며, 높은 정밀도와 다양한 크기의 값을 처리할 수 있어야 합니다.

3. 금융 분석

   • 복잡한 금융 모델링과 위험 평가에서는 높은 수준의 정밀도가 필요할 수 있으며, 부동 소수점 연산이 적합할 수 있습니다.

4. 컴퓨터 시뮬레이션

   • 물리적 시스템의 시뮬레이션은 넓은 범위의 값과 높은 정밀도를 요구하기 때문에, 부동 소수점 연산이 필수적입니다.

결론.

• 고정 소수점은 주로 리소스가 제한적이고 높은 정밀도가 필요하지 않은 환경에서 사용됩니다.
• 부동 소수점은 더 넓은 범위와 높은 정밀도를 필요로 하는 복잡한 계산에 적합합니다.
• 현대 프로세서의 경우, 부동 소수점 연산의 속도도 매우 빨라져서 예전만큼 고정 소수점과 부동 소수점 사이의 성능 차이가 크지 않을 수 있습니다.