Here is our report. Here is an old thesis.
SFT (sparse Fourier transform) algorithms aim to perform discrete Fourier transform in O(S) time, ignoring log factors, where S is the sparsity in frequency domain. In other words, the solution has a support of size S, plus some noise.
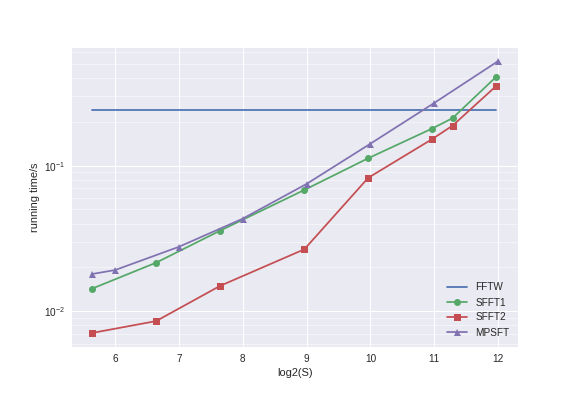
In MPSFT (Matrix Pencil Sparse Fourier Transform), we apply the matrix pencil method to improve the accuracy of mode identification and to reduce the chance of creating spurious modes (and having to correct them later). It makes SFT algorithms more feasible and practical. For N=2^22, we are faster than FFTW when S is less than around 1800. Previously, the fastest SFT algorithm that has a runtime of O(S) is faster for a much smaller range of S (around <= 200).
In the plot below, we fix N=2^22 and vary S (sparsity) and plot the running time. SFFT1 and SFFT2 are faster but they have a runtime of O(sqrt(NS)) ignoring log factors.
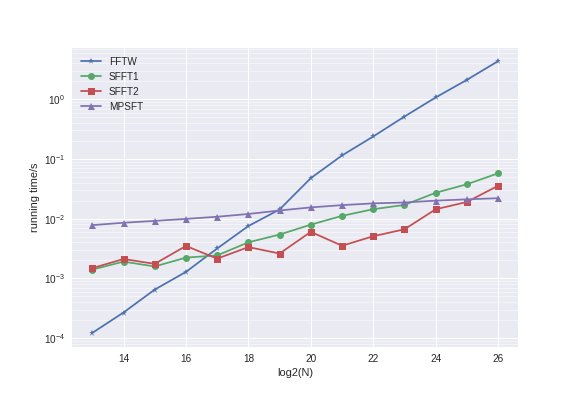
In the plot below, we fix K=50 and increase N.
For more details, please check out the report above.
For now, we will use the GPL license. This is mainly due to our use of FFTW. We do intend to move away from that in the near future, say using KissFFT.
We use Bazel (aka Blaze at Google). Do take a look at .bazelrc and modify accordingly.
MPSFT will need FFTW to perform FFT on much smaller vectors.
For comparison purposes, it is also good to build FFTW from source optimized for your machine.
./configure --enable-shared --enable-threads --enable-openmp
make
make installWe use Eigen though this dependency should probably be removed. It would be convenient to make install so that the headers are more accessible.
We run benchmarks using Google benchmarks. Remember to build using release mode.
mkdir build
cd build
cmake -DCMAKE_BUILD_TYPE=Release ../
make
sudo make installAfter that, make a symbolic link to the static lib in the src directory. You should be able to build :benchmark as a quick test.
ln -s /usr/local/lib/libbenchmark.a libbenchmark.aMake sure CPU scaling is turned off. See miscel section. Make sure everything is compiled from source and optimized for your machine. Make sure we use only a single core for fair comparison. (It is easy to parallelize. We do that later.)
bazel build --config=opt :binner_bench
./bazel-bin/binner_bench---------------------------------------------------------
Benchmark Time CPU Iterations
---------------------------------------------------------
BM_BinInTime/0/22 51322353 ns 51313717 ns 14
BM_BinInTime/1/22 34020450 ns 33825153 ns 21
BM_BinInTime/2/22 15582897 ns 15464899 ns 45
BM_BinInTime/3/22 15502842 ns 15498434 ns 46
BM_BinInTime/4/22 13180163 ns 13177513 ns 53
BM_BinInFreq/0/22 189558 ns 189515 ns 3693
BM_BinInFreq/1/22 91830 ns 91742 ns 7624
The first parameter selects the binner. The second parameter is log2(n).
From V0 to V1 for both BinInTime and BinInFreq, we exploit symmetry to roughly halve the number of trigonometric operations.
From V1 to V2 and BinInTime, we do some vectorization and also some Chebyshev approximation of sines and cosines. However, this introduces some errors which might accumulate and slow down convergence. They are also not the most robust.
From V2 to V3 and BinInTime, we switch to using Boost SIMD just for the sines and cosines computation. The speed is the same but the precision is way better.
From V3 to V4 and BinInTime, we vectorize more by splitting early into real and imaginary components.
As expected, FFTW is a lot faster when n is a power of 2. Hence, for benchmarking FFTW, we shall only use powers of 2. The FFTW plan flags used are either FFTW_ESTIMATE or FFTW_MEASURE. The latter will tell FFTW to plan harder. We do not use that in MPSFT. But for benchmarking, we will consider both. The first set of results uses FFTW_ESTIMATE. The second set of results uses FFTW_MEASURE.
-----------------------------------------------------------
Benchmark Time CPU Iterations
-----------------------------------------------------------
BM_FFTW/512/64 2784 ns 2785 ns 251328
BM_FFTW/1024/64 7057 ns 7059 ns 98574
BM_FFTW/2048/64 16129 ns 16132 ns 43301
BM_FFTW/4096/64 43010 ns 43025 ns 16215
BM_FFTW/8192/64 100024 ns 100037 ns 7000
BM_FFTW/16384/64 216689 ns 216756 ns 3208
BM_FFTW/32768/64 562530 ns 562611 ns 1233
BM_FFTW/65536/64 1081297 ns 1081531 ns 646
BM_FFTW/131072/64 2553803 ns 2554061 ns 278
BM_FFTW/262144/64 6379433 ns 6381363 ns 107
BM_FFTW/524288/64 13313930 ns 13317937 ns 54
BM_FFTW/1048576/64 44782775 ns 44791387 ns 16
BM_FFTW/2097152/64 106720464 ns 106719305 ns 6
BM_FFTW/4194304/64 225274535 ns 225334617 ns 3
BM_FFTW/8388608/64 481276039 ns 481304161 ns 2
BM_FFTW/16777216/64 1065906592 ns 1066002488 ns 1
BM_FFTW/33554432/64 2128920804 ns 2129135073 ns 1
BM_FFTW/67108864/64 4910248197 ns 4910418695 ns 1
BM_FFTW/512/0 2656 ns 2656 ns 264675
BM_FFTW/1024/0 5680 ns 5680 ns 122469
BM_FFTW/2048/0 12892 ns 12894 ns 54325
BM_FFTW/4096/0 29686 ns 29689 ns 23483
BM_FFTW/8192/0 66266 ns 66262 ns 10555
BM_FFTW/16384/0 150574 ns 150589 ns 4620
BM_FFTW/32768/0 336730 ns 336759 ns 2075
BM_FFTW/65536/0 727801 ns 727724 ns 961
BM_FFTW/131072/0 1547164 ns 1547240 ns 452
BM_FFTW/262144/0 3920139 ns 3919367 ns 178
BM_FFTW/524288/0 9995230 ns 9995484 ns 70
BM_FFTW/1048576/0 22117878 ns 22117107 ns 31
BM_FFTW/2097152/0 48003328 ns 47998012 ns 15
BM_FFTW/4194304/0 102253167 ns 102220593 ns 7
BM_FFTW/8388608/0 213492117 ns 213439206 ns 3
BM_FFTW/16777216/0 446109139 ns 445996409 ns 2
BM_FFTW/33554432/0 949558592 ns 949981237 ns 1
BM_FFTW/67108864/0 1987623996 ns 1987469827 ns 1
We use the following parameters.
n = 2^22
window_delta = 1e-5
window_threshold = 0.1
max_stale_iter = 5
min_bins = 51
sigma = 0.1
Here are the results. We see that the sparsity has to be around 1000 in order for MPSFT to be faster than FFTW.
bazel build --config=opt :demo1_bench
./bazel-bin/demo1_bench
./bazel-bin/demo1_bench \
--benchmark_repetitions=10 \
--benchmark_report_aggregates_only \
--benchmark_format=csvResults:
-------------------------------------------------------------
Benchmark Time CPU Iterations
-------------------------------------------------------------
BM_Demo1/4194301/64 19377235 ns 19362666 ns 35
BM_Demo1/4194301/128 27925545 ns 27918524 ns 26
BM_Demo1/4194301/256 42799864 ns 42788946 ns 16
BM_Demo1/4194301/512 75832472 ns 75829542 ns 8
BM_Demo1/4194301/1024 140758228 ns 140741482 ns 5
BM_Demo1/4194301/2048 263362872 ns 263305957 ns 3
BM_Demo1/4194301/4096 502254839 ns 502098835 ns 1
BM_Demo1/8191/50 7747979 ns 7746307 ns 91
BM_Demo1/16381/50 8427378 ns 8425902 ns 87
BM_Demo1/32771/50 9059204 ns 9056464 ns 78
BM_Demo1/65537/50 9837977 ns 9836558 ns 71
BM_Demo1/131071/50 10522716 ns 10519329 ns 65
BM_Demo1/262147/50 11284314 ns 11284282 ns 60
BM_Demo1/524287/50 13438242 ns 13436563 ns 54
BM_Demo1/1048573/50 14808361 ns 14807199 ns 47
BM_Demo1/2097143/50 16005829 ns 16001887 ns 43
BM_Demo1/4194301/50 17459595 ns 17456724 ns 39
BM_Demo1/8388617/50 18360027 ns 18354558 ns 37
BM_Demo1/16777213/50 20521324 ns 20519239 ns 34
A couple of parameters are not the most aggressive. For example, window_delta can be slightly bigger.
We use trials=1 because there is quite little noise here and there is no need to do any probability amplification. We expect trials to be odd and the running time is roughly proportional to trials. So using trials=3 will slow us down by ~3X.
Install gperftools. Link binary to this.
bazel build --config=opt --linkopt="-lprofiler" :demo1_main
BIN=./bazel-bin/demo1_main
$BIN
DATE=20170722
pprof --svg $BIN /tmp/demo1_main.prof > profile/demo1_main_${DATE}.svg
pprof --pdf $BIN /tmp/demo1_main.prof > profile/demo1_main_${DATE}.pdf
pprof --text $BIN /tmp/demo1_main.prof > profile/demo1_main_${DATE}.txt
pprof $BIN /tmp/demo1_main.profWe see that BinInTime takes up most of the running time.
Total: 164 samples
81 49.4% 49.4% 152 92.7% mps::BinInTimeV2::Run
54 32.9% 82.3% 57 34.8% sincos
14 8.5% 90.9% 14 8.5% __muldc3
4 2.4% 93.3% 4 2.4% __fmod_finite
3 1.8% 95.1% 3 1.8% nearbyint
2 1.2% 96.3% 2 1.2% gammal
1 0.6% 97.0% 2 1.2% Eigen::internal::svd_precondition_2x2_block_to_be_real::run
1 0.6% 97.6% 1 0.6% __nss_passwd_lookup
1 0.6% 98.2% 1 0.6% apply@1ee10
1 0.6% 98.8% 1 0.6% boost::math::detail::erf_imp
1 0.6% 99.4% 1 0.6% fmod
1 0.6% 100.0% 8 4.9% mps::BinInFreqV1::Run
0 0.0% 100.0% 2 1.2% Eigen::JacobiSVD::compute
0 0.0% 100.0% 164 100.0% __libc_start_main
Here is the visualization.
After tweaking sin-cos operations, such that it is almost 10X faster, we have:
Total: 96 samples
71 74.0% 74.0% 89 92.7% mps::BinInTimeV2::Run
18 18.8% 92.7% 18 18.8% mps::SinCosTwoPi
2 2.1% 94.8% 2 2.1% Eigen::internal::real_2x2_jacobi_svd
2 2.1% 96.9% 2 2.1% t2_25
1 1.0% 97.9% 3 3.1% apply@1b6f0
1 1.0% 99.0% 4 4.2% mps::BinInFreqV1::Run
1 1.0% 100.0% 1 1.0% mps::Window::Window
0 0.0% 100.0% 2 2.1% Eigen::JacobiSVD::compute
Here is the visualization.
Unfortunately, the sin-cos earlier is not precise or robust enough. We switched to using Boost.SIMD just for this part. The new profile results is:
Total: 69 samples
48 69.6% 69.6% 55 79.7% mps::BinInTimeV4::Run
12 17.4% 87.0% 12 17.4% sincos
4 5.8% 92.8% 12 17.4% mps::BinInFreqV1::Run
2 2.9% 95.7% 2 2.9% gammal
2 2.9% 98.6% 2 2.9% t2_25
1 1.4% 100.0% 1 1.4% erf
0 0.0% 100.0% 69 100.0% __libc_start_main
0 0.0% 100.0% 69 100.0% _start
0 0.0% 100.0% 2 2.9% apply@1b6f0
0 0.0% 100.0% 2 2.9% apply@1cad0
Here is the visualization.
Switch between performance and powersave.
cat /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor
for CPUFREQ in /sys/devices/system/cpu/cpu*/cpufreq/scaling_governor; do [ -f $CPUFREQ ] || continue; echo -n performance > $CPUFREQ; done