1168

1168. Optimize Water Distribution in a Village (Hard)

There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.

For each house i, we can either build a well inside it directly with cost wells[i - 1] (note the -1 due to 0-indexing), or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[j] = [house1j, house2j, costj] represents the cost to connect house1j and house2j together using a pipe. Connections are bidirectional.

Return the minimum total cost to supply water to all houses.

 

Example 1:

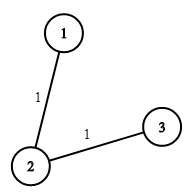
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation: 
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.

 

Constraints:

• 1 <= n <= 104
• wells.length == n
• 0 <= wells[i] <= 105
• 1 <= pipes.length <= 104
• pipes[j].length == 3
• 1 <= house1j, house2j <= n
• 0 <= costj <= 105
• house1j != house2j

Companies:
Google, Facebook, Yahoo

Related Topics:
Union Find, Graph, Minimum Spanning Tree

Solution 1. Greedy

// OJ: https://leetcode.com/problems/optimize-water-distribution-in-a-village/
// Author: github.com/lzl124631x
// Time: O(E + (V + E) * log(V + E))
// Space: O(E + V)
class Solution {
public:
    int minCostToSupplyWater(int n, vector<int>& W, vector<vector<int>>& P) {
        vector<vector<pair<int, int>>> G(n);
        for (auto &p : P) {
            int u = p[0] - 1, v = p[1] - 1, cost = p[2];
            G[u].emplace_back(v, cost);
            G[v].emplace_back(u, cost);
        }
        unordered_set<int> seen;
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq; // cost, index
        for (int i = 0; i < n; ++i) pq.emplace(W[i], i);
        int ans = 0;
        while (seen.size() < n) {
            auto [cost, u] = pq.top();
            pq.pop();
            if (seen.count(u)) continue;
            seen.insert(u);
            ans += cost;
            for (auto &[v, c] : G[u]) {
                if (seen.count(v)) continue;
                pq.emplace(c, v);
            }
        }
        return ans;
    }
};