Skip to content

Latest commit

 

History

History
111 lines (104 loc) · 5.26 KB

README.md

File metadata and controls

111 lines (104 loc) · 5.26 KB
Raw

2603. Collect Coins in a Tree (Hard)

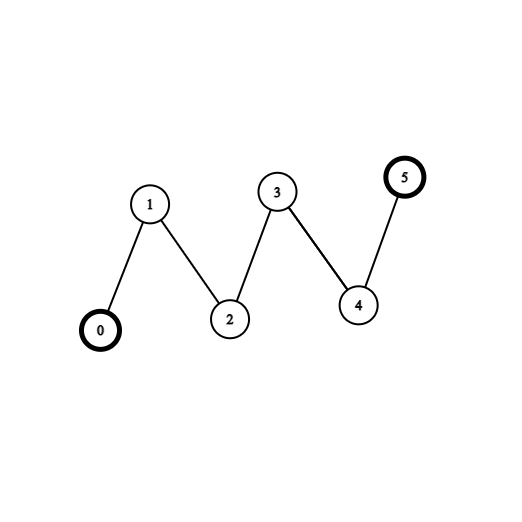
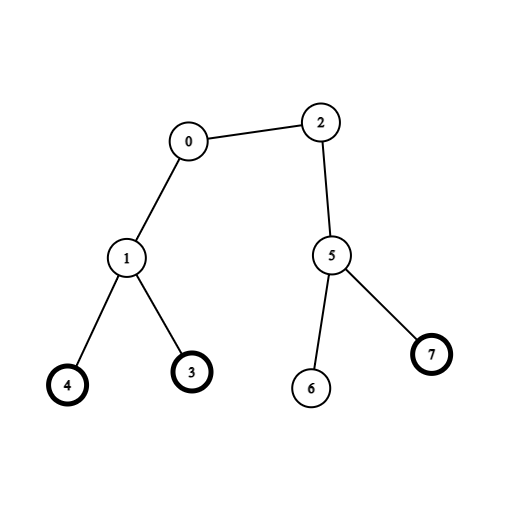
There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given an integer n and a 2D integer array edges of length n - 1, where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an array coins of size n where coins[i] can be either 0 or 1, where 1 indicates the presence of a coin in the vertex i.

Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times: 

  • Collect all the coins that are at a distance of at most 2 from the current vertex, or
  • Move to any adjacent vertex in the tree.

Find the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex.

Note that if you pass an edge several times, you need to count it into the answer several times.

 

Example 1:

Input: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]
Output: 2
Explanation: Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.

Example 2:

Input: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]
Output: 2
Explanation: Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2,  collect the coin at vertex 7, then move back to vertex 0.

 

Constraints:

  • n == coins.length
  • 1 <= n <= 3 * 104
  • 0 <= coins[i] <= 1
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • edges represents a valid tree.

Companies: Uber, Lucid

Related Topics:
Array, Tree, Graph, Topological Sort

Similar Questions:

Solution 1. Topological Sort

  • Delete the nodes without coins from leaf node, until it reachs a node with coin or a non-leaf node
  • Now all the leaf nodes are with coins. Start from these leave nodes, delete two layer of nodes.
  • Count the number of edges connecting any remaining nodes. The answer is this number multiplied by 2.
// OJ: https://leetcode.com/problems/collect-coins-in-a-tree
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(N)
class Solution {
public:
    int collectTheCoins(vector<int>& A, vector<vector<int>>& E) {
        int N = A.size(), ans = 0;
        if (N <= 3) return 0;
        vector<vector<int>> G(N);
        vector<int> deg(N);
        vector<bool> del(N);
        for (auto &e : E) { // Built graph
            int u = e[0], v = e[1];
            G[u].push_back(v);
            G[v].push_back(u);
            deg[u]++;
            deg[v]++;
        }
        queue<int> q;
        for (int i = 0; i < N; ++i) { // Collect leaf nodes without coins and delete them
            if (deg[i] == 1 && A[i] == 0) {
                q.push(i);
                del[i] = true;
            }
        }
        while (q.size()) { // Keep deleting leaf nodes without coins
            int u = q.front();
            q.pop();
            for (int v : G[u]) {
                if (del[v]) continue;
                if (--deg[v] <= 1 && A[v] == 0) {
                    del[v] = true;
                    q.push(v);
                }
            }
        }
        for (int i = 0; i < N; ++i) { // Collect the leaf nodes with coins, and delete them
            if (deg[i] == 1 && !del[i]) {
                q.push(i);
                del[i] = true;
            }
        }
        while (q.size()) { // Delete one layer further from those leaf nodes
            int u = q.front();
            q.pop();
            for (int v : G[u]) {
                if (del[v]) continue;
                if (--deg[v] <= 1) del[v] = true;
            }
        }
        for (auto &e : E) { // Count the number of edges connecting undeleted nodes.
            ans += !del[e[0]] && !del[e[1]];
        }
        return ans * 2;
    }
};