298

298. Binary Tree Longest Consecutive Sequence (Medium)

Given the root of a binary tree, return the length of the longest consecutive sequence path.

The path refers to any sequence of nodes from some starting node to any node in the tree along the parent-child connections. The longest consecutive path needs to be from parent to child (cannot be the reverse).

 

Example 1:

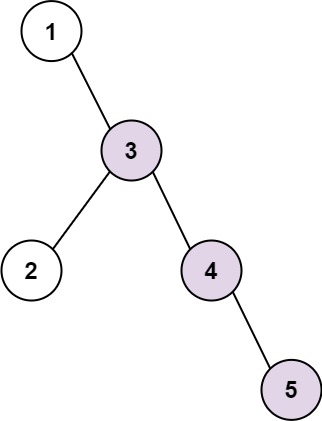
Input: root = [1,null,3,2,4,null,null,null,5]
Output: 3
Explanation: Longest consecutive sequence path is 3-4-5, so return 3.

Example 2:

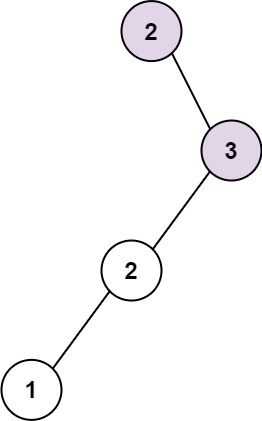
Input: root = [2,null,3,2,null,1]
Output: 2
Explanation: Longest consecutive sequence path is 2-3, not 3-2-1, so return 2.

 

Constraints:

• The number of nodes in the tree is in the range [1, 3 * 104].
• -3 * 104 <= Node.val <= 3 * 104

Companies:
ByteDance

Related Topics:
Tree, Depth-First Search, Binary Tree

Similar Questions:

• Longest Consecutive Sequence (Medium)
• Binary Tree Longest Consecutive Sequence II (Medium)

Solution 1. Pre-order Traversal

// OJ: https://leetcode.com/problems/binary-tree-longest-consecutive-sequence/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    int ans = 0;
    void dfs(TreeNode *root, TreeNode *parent = NULL, int length = 1) {
        if (!root) return;
        length = parent && parent->val + 1 == root->val ? length + 1 : 1;
        ans = max(ans, length);
        dfs(root->left, root, length);
        dfs(root->right, root, length);
    }
public:
    int longestConsecutive(TreeNode* root) {
        dfs(root);
        return ans;
    }
};

Solution 2. Post-order Traversal

// OJ: https://leetcode.com/problems/binary-tree-longest-consecutive-sequence/
// Author: github.com/lzl124631x
// Time: O(N)
// Space: O(H)
class Solution {
    int ans = 0;
    int dfs(TreeNode *root) {
        if (!root) return 0;
        int left = dfs(root->left), right = dfs(root->right);
        if (root->left && root->val + 1 != root->left->val) left = 0;
        if (root->right && root->val + 1 != root->right->val) right = 0;
        ans = max({ ans, 1 + left, 1 + right });
        return 1 + max(left, right);
    }
public:
    int longestConsecutive(TreeNode* root) {
        dfs(root);
        return ans;
    }
};