304

304. Range Sum Query 2D - Immutable (Medium)

Given a 2D matrix matrix, handle multiple queries of the following type:

• Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

• NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
• int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

You must design an algorithm where sumRegion works on O(1) time complexity.

 

Example 1:

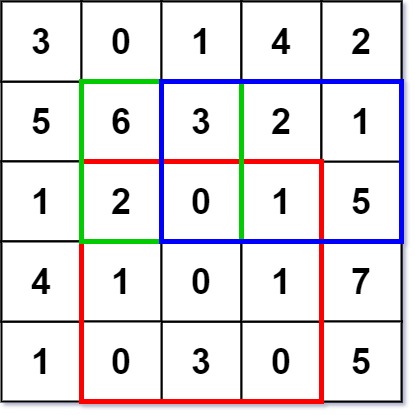
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]
Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

 

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -104 <= matrix[i][j] <= 104
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• At most 104 calls will be made to sumRegion.

Companies: Facebook, Lyft, Amazon, Google, Nvidia, Samsung, Uber, Snowflake

Related Topics:
Array, Design, Matrix, Prefix Sum

Similar Questions:

• Range Sum Query - Immutable (Easy)
• Range Sum Query 2D - Mutable (Hard)

Solution 1.

// OJ: https://leetcode.com/problems/range-sum-query-2d-immutable
// Author: github.com/lzl124631x
// Time:
//      NumMatrix: O(MN)
//      sumRegion: O(1)
// Space: O(MN)
class NumMatrix {
    vector<vector<int>> sum;
public:
    NumMatrix(vector<vector<int>>& A) {
        int M = A.size(), N = A[0].size();
        sum.assign(M + 1, vector<int>(N + 1));
        for (int i = 0; i < M; ++i) {
            int s = 0;
            for (int j = 0; j < N; ++j) {
                s += A[i][j];
                sum[i + 1][j + 1] = s + sum[i][j + 1];
            }
        }
    }
    int sumRegion(int row1, int col1, int row2, int col2) {
        return sum[row2 + 1][col2 + 1] - sum[row1][col2 + 1] - sum[row2 + 1][col1] + sum[row1][col1];
    }
};