-
Notifications
You must be signed in to change notification settings - Fork 291
/
gmm.md
40 lines (20 loc) · 1.82 KB
/
gmm.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
1)概述
正态分布也叫高斯分布,正态分布的概率密度曲线也叫高斯分布概率曲线_。_
GaussianMixtureModel\(混合高斯模型,GMM\)。
聚类算法大多数通过相似度来判断,而相似度又大多采用欧式距离长短作为衡量依据。而GMM采用了新的判断依据:概率,即通过属于某一类的概率大小来判断最终的归属类别。
GMM的基本思想就是:任意形状的概率分布都可以用多个高斯分布函数去近似,也就是说GMM就是有多个单高斯密度分布(Gaussian)组成的,每个Gaussian叫一个"Component",这些"Component"线性加成在一起就组成了 GMM 的概率密度函数,也就是下面的函数。
2)数学公式
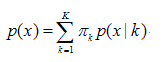
K:模型的个数,即Component的个数(聚类的个数)
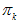为第k个高斯的权重
p(x \|k) 则为第k个高斯概率密度,其均值为μk,方差为σk
上述参数,除了K是直接给定之外,其他参数都是通过EM算法估算出来的。\(有个参数是指定EM算法参数的\)
3)GaussianMixtureModel 算法函数
a)from sklearn.mixture.GaussianMixture
b)主要参数([详细参数](http://scikit-learn.org/dev/modules/generated/sklearn.mixture.GaussianMixture.html#sklearn.mixture.GaussianMixture))
n\_components :高斯模型的个数,即聚类的目标个数
covariance\_type : 通过EM算法估算参数时使用的协方差类型,默认是"full"
full:每个模型使用自己的一般协方差矩阵
tied:所用模型共享一个一般协方差矩阵
diag:每个模型使用自己的对角线协方差矩阵
spherical:每个模型使用自己的单一方差