-
Notifications
You must be signed in to change notification settings - Fork 291
/
gaosi-kernel.md
154 lines (97 loc) · 9.49 KB
/
gaosi-kernel.md
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
# [支持向量机高斯核调参小结](http://www.cnblogs.com/pinard/p/6126077.html)
在支持向量机\(以下简称SVM\)的核函数中,高斯核\(以下简称RBF\)是最常用的,从理论上讲, RBF一定不比线性核函数差,但是在实际应用中,却面临着几个重要的超参数的调优问题。如果调的不好,可能比线性核函数还要差。所以我们实际应用中,能用线性核函数得到较好效果的都会选择线性核函数。如果线性核不好,我们就需要使用RBF,在享受RBF对非线性数据的良好分类效果前,我们需要对主要的超参数进行选取。本文我们就对scikit-learn中 SVM RBF的调参做一个小结。
# 1. SVM RBF 主要超参数概述
如果是SVM分类模型,这两个超参数分别是惩罚系数C和RBF核函数的系数$$\gamma$$。当然如果是nu-SVC的话,惩罚系数C代替为分类错误率上限nu, 由于惩罚系数C和分类错误率上限nu起的作用等价,因此本文只讨论带惩罚系数C的分类SVM。
惩罚系数C即我们在之前原理篇里讲到的松弛变量的系数。它在优化函数里主要是平衡支持向量的复杂度和误分类率这两者之间的关系,可以理解为正则化系数。当C比较大时,我们的损失函数也会越大,这意味着我们不愿意放弃比较远的离群点。这样我们会有更加多的支持向量,也就是说支持向量和超平面的模型也会变得越复杂,也容易过拟合。反之,当C比较小时,意味我们不想理那些离群点,会选择较少的样本来做支持向量,最终的支持向量和超平面的模型也会简单。scikit-learn中默认值是1。
另一个超参数是RBF核函数的参数$$\gamma$$。回忆下RBF 核函数$$K(x, z) = exp(-\gamma||x-z||^2)\;\;\gamma>0$$,$$\gamma$$主要定义了单个样本对整个分类超平面的影响,当$$\gamma$$比较小时,单个样本对整个分类超平面的影响比较大,更容易被选择为支持向量,反之,当$$\gamma$$比较大时,单个样本对整个分类超平面的影响比较小,不容易被选择为支持向量,或者说整个模型的支持向量也会少。scikit-learn中默认值是$$\frac{1}{num-samples}$$
如果把惩罚系数C和RBF核函数的系数$$\gamma$$一起看,当C比较大, $$\gamma$$比较小时,我们会有更多的支持向量,我们的模型会比较复杂,容易过拟合一些。如果C比较小 , $$\gamma$$比较大时,模型会变得简单,支持向量的个数会少。
以上是SVM分类模型,我们再来看看回归模型。
SVM回归模型的RBF核比分类模型要复杂一点,因为此时我们除了惩罚系数C和RBF核函数的系数$$\gamma$$之外,还多了一个损失距离度量$$\epsilon$$。如果是nu-SVR的话,损失距离度量$$\epsilon$$代替为分类错误率上限nu,由于损失距离度量$$\epsilon$$和分类错误率上限nu起的作用等价,因此本文只讨论带距离度量$$\epsilon$$的回归SVM。
对于惩罚系数C和RBF核函数的系数$$\gamma$$,回归模型和分类模型的作用基本相同。对于损失距离度量$$\epsilon$$,它决定了样本点到超平面的距离损失,当$$\epsilon$$比较大时,损失$$|y_i - w \bullet \phi(x_i ) -b| - \epsilon$$较小,更多的点在损失距离范围之内,而没有损失,模型较简单,而当$$\epsilon$$比较小时,损失函数会较大,模型也会变得复杂。scikit-learn中默认值是0.1。
如果把惩罚系数C,RBF核函数的系数$$\gamma$$和损失距离度量$$\epsilon$$一起看,当C比较大,$$\gamma$$比较小,$$\epsilon$$比较小时,我们会有更多的支持向量,我们的模型会比较复杂,容易过拟合一些。如果C比较小 ,$$\gamma$$比较大,$$\epsilon$$比较大时,模型会变得简单,支持向量的个数会少。
# 2. SVM RBF 主要调参方法
对于SVM的RBF核,我们主要的调参方法都是交叉验证。具体在scikit-learn中,主要是使用网格搜索,即GridSearchCV类。当然也可以使用cross\_val\_score类来调参,但是个人觉得没有GridSearchCV方便。本文我们只讨论用GridSearchCV来进行SVM的RBF核的调参。
我们将GridSearchCV类用于SVM RBF调参时要注意的参数有:
1\) estimator :即我们的模型,此处我们就是带高斯核的SVC或者SVR
2\) param\_grid:即我们要调参的参数列表。 比如我们用SVC分类模型的话,那么param\_grid可以定义为{"C":\[0.1, 1, 10\], "gamma": \[0.1, 0.2, 0.3\]},这样我们就会有9种超参数的组合来进行网格搜索,选择一个拟合分数最好的超平面系数。
3\) cv: S折交叉验证的折数,即将训练集分成多少份来进行交叉验证。默认是3,。如果样本较多的话,可以适度增大cv的值。
网格搜索结束后,我们可以得到最好的模型estimator, param\_grid中最好的参数组合,最好的模型分数。
下面我用一个具体的分类例子来观察SVM RBF调参的过程
# 3. 一个SVM RBF分类调参的例子
这里我们用一个实例来讲解SVM RBF分类调参。推荐在ipython notebook运行下面的例子。
首先我们载入一些类的定义。
```
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets, svm
from sklearn.svm import SVC
from sklearn.datasets import make_moons, make_circles, make_classification
%matplotlib inline
```
接着我们生成一些随机数据来让我们后面去分类,为了数据难一点,我们加入了一些噪音。生成数据的同时把数据归一化
```
X, y = make_circles(noise=0.2, factor=0.5, random_state=1);
from sklearn.preprocessing import StandardScaler
X = StandardScaler().fit_transform(X)
```
我们先看看我的数据是什么样子的,这里做一次可视化如下:
```
from matplotlib.colors import ListedColormap
cm = plt.cm.RdBu
cm_bright = ListedColormap(['#FF0000', '#0000FF'])
ax = plt.subplot()
ax.set_title("Input data")
# Plot the training points
ax.scatter(X[:, 0], X[:, 1], c=y, cmap=cm_bright)
ax.set_xticks(())
ax.set_yticks(())
plt.tight_layout()
plt.show()
```
生成的图如下, 由于是随机生成的所以如果你跑这段代码,生成的图可能有些不同。
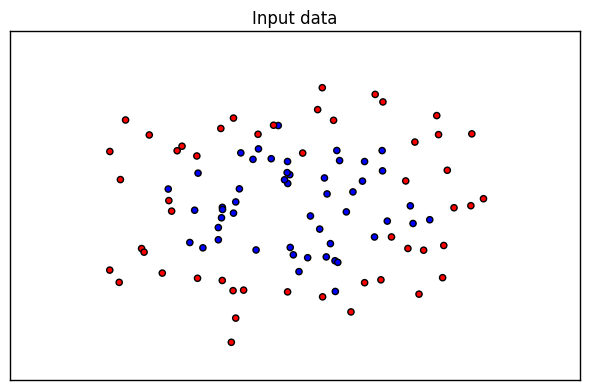
好了,现在我们要对这个数据集进行SVM RBF分类了,分类时我们使用了网格搜索,在C=\(0.1,1,10\)和gamma=\(1, 0.1, 0.01\)形成的9种情况中选择最好的超参数,我们用了4折交叉验证。这里只是一个例子,实际运用中,你可能需要更多的参数组合来进行调参。
```
from sklearn.model_selection import GridSearchCV
grid = GridSearchCV(SVC(), param_grid={"C":[0.1, 1, 10], "gamma": [1, 0.1, 0.01]}, cv=4)
grid.fit(X, y)
print("The best parameters are %s with a score of %0.2f"
% (grid.best_params_, grid.best_score_))
```
最终的输出如下:
The best parameters are {'C': 10, 'gamma': 0.1} with a score of 0.91
也就是说,通过网格搜索,在我们给定的9组超参数中,C=10, Gamma=0.1 分数最高,这就是我们最终的参数候选。
到这里,我们的调参举例就结束了。不过我们可以看看我们的普通的SVM分类后的可视化。这里我们把这9种组合各个训练后,通过对网格里的点预测来标色,观察分类的效果图。代码如下:
```
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max,0.02),
np.arange(y_min, y_max, 0.02))
for i, C in enumerate((0.1, 1, 10)):
for j, gamma in enumerate((1, 0.1, 0.01)):
plt.subplot()
clf = SVC(C=C, gamma=gamma)
clf.fit(X,y)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.8)
# Plot also the training points
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.coolwarm)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())
plt.xticks(())
plt.yticks(())
plt.xlabel(" gamma=" + str(gamma) + " C=" + str(C))
plt.show()
```
生成的9个组合的效果图如下:
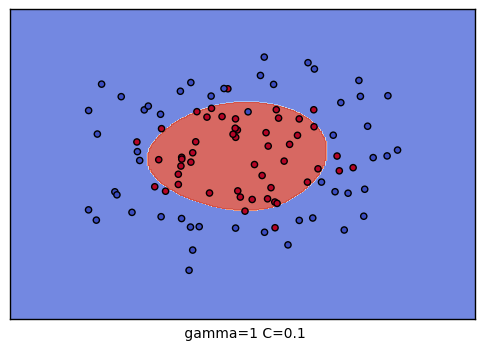


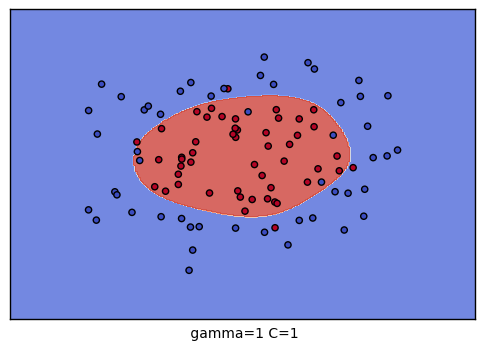
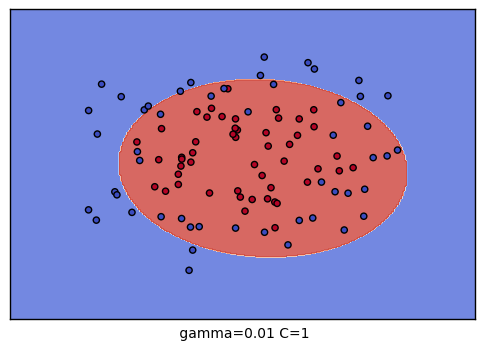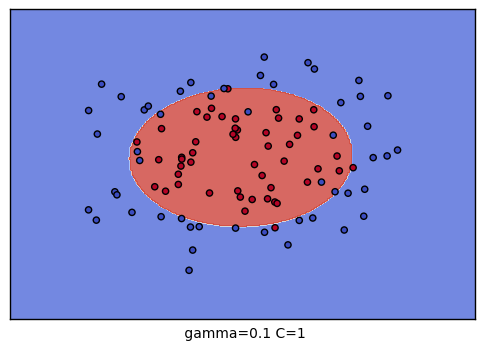
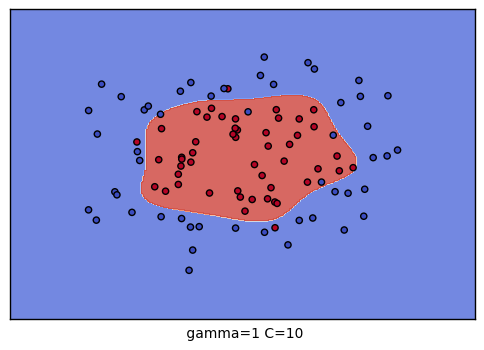


以上就是SVM RBF调参的一些总结,希望可以帮到朋友们。