-
Notifications
You must be signed in to change notification settings - Fork 68
New issue
Have a question about this project? Sign up for a free GitHub account to open an issue and contact its maintainers and the community.
By clicking “Sign up for GitHub”, you agree to our terms of service and privacy statement. We’ll occasionally send you account related emails.
Already on GitHub? Sign in to your account
Child groups of "equal elevation"? #85
Comments
|
Hey @fosskers! Sure, happy to help :) I think what we really need here is breadth-first search, but we could start with a simpler but less efficient approach: -- Find the vertices that have no dependencies
-- O(n) complexity
leaves :: Ord a => AdjacencyMap a -> Set a
leaves x = Set.filter (null . flip postSet x) $ vertexSet x
-- Split a graph into batches of mutually independent vertices
-- Probably O(m * n * log(n)) complexity
batch :: Ord a => AdjacencyMap a -> [Set a]
batch g
| isEmpty g = []
| otherwise = ls : batch (induce (`Set.notMember` ls) g)
where
ls = leaves gSeems to do what you need, although produces the list in the reverse order. > g = edges [('A','C'), ('A','D'), ('B','D'), ('B','E'), ('C','F'), ('D','F'), ('E','G')]
> batch g
[fromList "FG",fromList "CDE",fromList "AB"]This is very suboptimal in terms of performance. BFS could do this in O(n + m) time. How large are your graphs? Perhaps this implementation is sufficient? It's advantage is that it's simple. If it's too slow, let's try to implement a BFS-based algorithm. |
|
I edited my comment above. I initially misjudged the complexity of my solution, but then remembered that |
|
These graphs won't be too big for the average user (dozens of vertices at most), but I have gotten reports of people with ~300 packages needing updates, would could balloon into a 500+ vertex graph. |
|
I think my naive implementation will take sub-second time for graphs with <1000 vertices, so if you are going to do anything non-trivial with the packages, e.g. download or build them, it will be just noise. But I'm still interested in implementing a fast version, so I'll keep thinking. |
|
Oh yeah, this app is completely IO-bound in terms of perf, so I suppose this isn't a worry. |
|
Alright, the algorithm as-is does work. For performance, I'm comparing the solving of dependencies for a very complicated package tree ( Timings
Sweet, so no real slowdown for big trees. |
|
@fosskers Great! I've been thinking about the algorithm I suggested and there is one peculiarity I'd like to highlight, since it may be surprising. The current implementation maximises concurrency among leaves, instead of maximising concurrency among roots. For example, if you have a graph with three vertices Note that in general, neither of these two schedules is better than the other. If the tasks take time |
|
The "leaves first" approach is probably fine, considering that the leaves here are package dependencies that need to be built and installed before their parents can be built. |
|
I see, sounds good. Do you need any further help with Alga? If not, I guess we can close this issue. |
|
Yup, case closed, I think! Thank you very much. |
|
No problem, happy to help again in future. |
Hi there, I'm the author of a particular package manager written in Haskell. About 6 months ago you offered your help for when I reached the stage of evaluating
algebraic-graphs. I'm there now, so hi!Here's the general problem I'm looking to solve:
Packages on a Linux system have dependencies, and these dependency relationships form a graph. I'd like to implement the function:
the return value of which corresponds to the following:
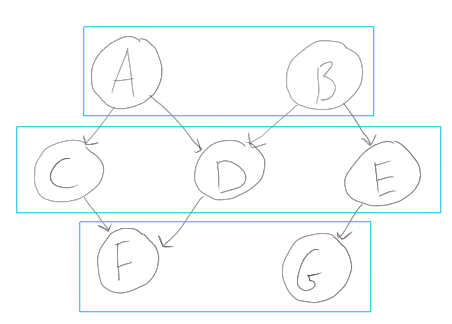
Each cyan box of packages are sibling-like and "safe" to build and install at the same time, since they aren't interdependent. For this example, I'd expect the output of
sortPackagesto resemble:Looking at your API, I suspect these functions are probably what I'm looking for. In the current version of my code, I'm using
topSortfromData.Graphto naively get the overall safe ordering, then building one-at-a-time sincetopSortloses other "elevation information".Can
algebraic-graphshelp me here?Please and thanks,
Colin
The text was updated successfully, but these errors were encountered: