N/A :calendar: Chapter completed on June 2 2020 🎉
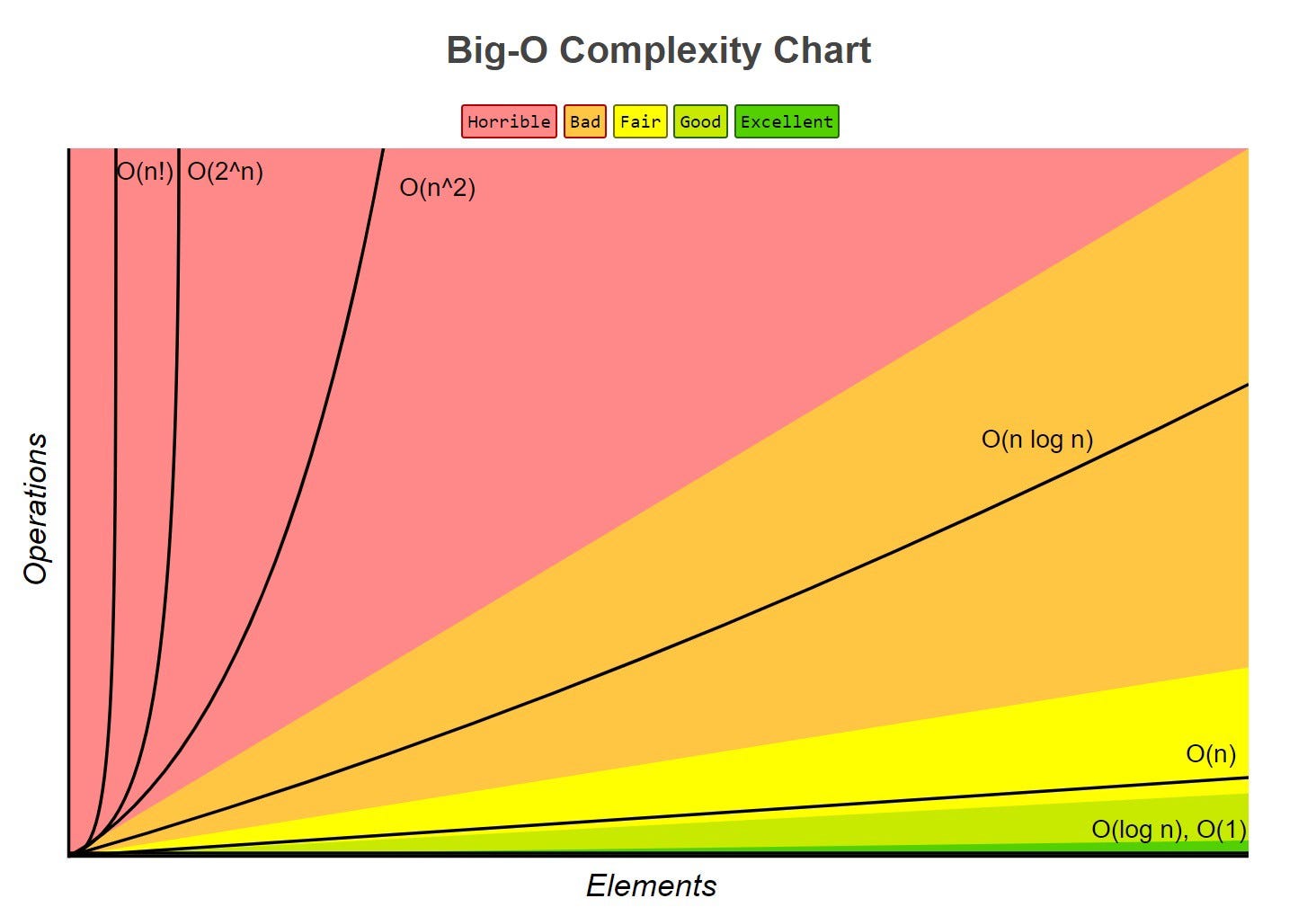
Big O, or asymptotic runtime, is the language and metric we use to describe the efficiency of algorithms. Big O describes the rate of increase -- no matter the size of the constant is or how slow the linear increase is, linear will at some point surpass the constant.
We rarely ever discuss best case time complexity, because it's not a very useful concept. After all, we could take essentially any algorithm, special case some input, and then get an O(1) runtime in the best case. For many -- probably most -- algorithms, the worst case and expected case are the same.
Caused by specific input or just unluckiness, the worst case is the slowest run time of an algorithm. Perhaps in quick sort, your pivot is the first element in a reverse-ordered array so each recursive step only shrinks the subarray by 1 element instead of splitting the array in half.
The average runtime, in which the worst case isn't repeating itself recursively.
If we need to create an array of size n, this will require O(n) space. If we need a two-dimensional array of size n by n, this will require O(n^2) space.
Stack space in recurive calls count too! But just because you have n calls doesn't mean it takes O(n) space. Example: Looping through a list ([0, 1, 2, 3, 4, ...]) and adding adjacent numbers using a pairSum() helper method doesn't add more space to the call stack.
Constants are dropped in Big O because O(n) could potentially run faster than O(1). Similarly, O(2 n) is simplified to O(n).
In practice, one O(n) algorithm might be much faster than another -- and the O(n^2 algorithm might be faster than both on some inputs.)
- O(n^2 + n) => O(n^2)
- O(n + log n) => O(n)
- O((5 * 2^n) + (1000 * n^100) => O(2^n)
If your algorithm is in the form "do this, then, when you're all done, do that" then you add the runtimes. If your algorithm is in the form "do this for each time you do that" then you multiply the runtimes.
Consider you have a list of size n. You add an item to the list, and the array reaches its capacity, so it must dynamically resize. To create an array of size 2n and copy over n elements will take O(n) time. However, this occurrence is rare -- amortized time takes note of that.
When you see a problem where the number of elements in the problem space gets halved each time, that will likely be a O(log n) runtime.
When you have a recursive function that makes multiple calls, the runtime will often (but not always) look like O(branches^depth), where branches is the number of times each recursive call branches.