A chainable timeseries analysis tool.
Transform your data, filter it, smooth it, remove the noise, get stats, get a preview chart of the data, ...
This lib was conceived to analyze noisy financial data but is suitable to any type of timeseries.
npm install timeseries-analysis
var timeseries = require("timeseries-analysis");
This package is in early alpha, and is currently under active development.
The format or name of the methods might change in the future.
The data must be in the following format:
var data = [
[date, value],
[date, value],
[date, value],
...
];
date can be in any format you want, but it is recommanded you use date value that is comaptible with a JS Date object.
value must be a number.
// Load the data
var t = new timeseries.main(data);
Alternatively, you can also load the data from your database:
// Unfiltered data out of MongoDB:
var data = [{
"_id": "53373f538126b69273039245",
"adjClose": 26.52,
"close": 26.52,
"date": "2013-04-15T03:00:00.000Z",
"high": 27.48,
"low": 26.36,
"open": 27.16,
"symbol": "fb",
"volume": 30275400
},
{
"_id": "53373f538126b69273039246",
"adjClose": 26.92,
"close": 26.92,
"date": "2013-04-16T03:00:00.000Z",
"high": 27.11,
"low": 26.4,
"open": 26.81,
"symbol": "fb",
"volume": 27365900
},
{
"_id": "53373f538126b69273039247",
"adjClose": 26.63,
"close": 26.63,
"date": "2013-04-17T03:00:00.000Z",
"high": 27.2,
"low": 26.39,
"open": 26.65,
"symbol": "fb",
"volume": 26440600
},
...
];
// Load the data
var t = new timeseries.main(timeseries.adapter.fromDB(data, {
date: 'date', // Name of the property containing the Date (must be compatible with new Date(date) )
value: 'close' // Name of the property containign the value. here we'll use the "close" price.
}));
This is the data I will use in the doc:
Finaly, you can load the data from an array:
// Data out of MongoDB:
var data = [12,16,14,13,11,10,9,11,23,...];
// Load the data
var t = new timeseries.main(timeseries.adapter.fromArray(data));
You can chain the methods. For example, you can calculate the moving average, then apply a Linear Weighted Moving Average on top of the first Moving Average:
t.ma().lwma();
When you are done processing the data, you can get the processed timeseries using output():
var processed = t.ma().output();
You can plot your data using Google Static Image Chart, as simply as calling the chart() method:
var chart_url = t.ma({period: 14}).chart();
// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:JDOLhghn0s92xuilnptvxz1110zzzyyvrlgZUPMHA&chco=76a4fb&chm=&chds=63.13,70.78&chxr=0,63.13,70.78,10
You can include the original data in your chart:
var chart_url = t.ma({period: 14}).chart({main:true});
// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:ebgfqpqtzv40yxrstuwxyz000zzzzyyxvsqmjhfdZ,ebgfqpqtzv40yxvrw740914wswyupqdgPRNOXYLAB&chco=76a4fb,ac7cc7&chm=&chds=56.75,72.03&chxr=0,56.75,72.03,10
You can chart more than one dataset, using the save() method. You can use the reset() method to reset the buffer.
save() will save a copy the current buffer and add it to the list of datasets to chart.
reset() will reset the buffer back to its original data.
// Chart the Moving Average and a Linear Weighted Moving Average on on the same chart, in addition to the original data:
var chart_url = t.ma({period: 8}).save('moving average').reset().lwma({period:8}).save('LWMA').chart({main:true});
// returns https://chart.googleapis.com/chart?cht=lc&chs=800x200&chxt=y&chd=s:ebgfqpqthjnptuwyzyzyxyy024211yxusrojfbWUQ,ebgfqpqtzv40yxvrw740914wswyupqdgPRNOXYLAB,ebgfqpqtknqtvwxyxxyyy0022200zwvrpmidZXVTP,ebgfqpqthjnptuwyzyzyxyy024211yxusrojfbWUQ&chco=76a4fb,9190e1,ac7cc7,c667ad&chm=&chds=56.75,72.03&chxr=0,56.75,72.03,10
You can obtain stats about your data. The stats will be calculated based on the current buffer.
var min = t.min(); // 56.75
var max = t.max(); // 72.03
var mean = t.mean(); // 66.34024390243898
var stdev = t.stdev(); // 3.994277911972647
There are a few smoothing options implemented:
t.ma({
period: 6
});
t.lwma({
period: 6
});
Created by John Ehlers to smooth noisy data without lag. alpha must be between 0 and 1.
t.dsp_itrend({
alpha: 0.7
});
Most smoothing algorithms induce lag in the data. Algorithms like Ehler's iTrend algorithm has no lag, but won't be able to perform really well on a really noisy dataset as you can see in the example above.
For that reason, this package has a set of lagless noise-removal and noise-separation algorithms.
t.smoother({
period: 10
});
You can extract the noise from the signal.
t.smoother({period:10}).noiseData();
// Here, we add a line on y=0, and we don't display the orignal data.
var chart_url = t.chart({main:false, lines:[0]})
You can also smooth the noise, to attempt to find patterns:
t.smoother({period:10}).noiseData().smoother({period:5});
This package allows you to easily forecast future values by calculating the Auto-Regression (AR) coefficients for your data.
The AR coefficients can be calculated using both the Least Square and using the Max Entropy methods.
Both methods have a degree parameter that let you define what AR degree you wish to calculate. The default is 5.
Both methods were ported to Javascript for this package from Paul Bourke's C code. Credit to Alex Sergejew, Nick Hawthorn and Rainer Hegger for the original code of the Max Entropy method. Credit to Rainer Hegger for the original code of the Least Square method.
Let's generate a simple sin wave:
var t = new ts.main(ts.adapter.sin({cycles:4}));
Now we get the coefficients (default: degree 5) using the Max Entropy method:
var coeffs = t.ARMaxEntropy();
/* returns:
[
-4.996911311490191,
9.990105570823655,
-9.988844272139962,
4.995018589153196,
-0.9993685753936928
]
*/
Now let's calculate the coefficents using the Least Square method:
var coeffs = t.ARLeastSquare();
/* returns:
[
-0.1330958776419982,
1.1764459735164208,
1.3790630711914558,
-0.7736249950234015,
-0.6559429479401289
]
*/
To specify the degree:
var coeffs = t.ARMaxEntropy({degree: 3}); // Max Entropy method, degree 3
var coeffs = t.ARLeastSquare({degree: 7}); // Least Square method, degree 7.
Now, calculating the AR coefficients of the entire dataset might not be really useful for any type of real-life use.
You can specify what data you want to use to calculate the AR coefficients, allowing to use only a subset of your dataset using the data parameter:
// We'll use only the first 10 datapoints of the current data
var coeffs = t.ARMaxEntropy({
data: t.data.slice(0, 10)
});
/* returns:
[
-4.728362307674655,
9.12909005456654,
-9.002790480535127,
4.536763868018368,
-0.9347010551658372
]
*/
Now that we know how to calculate the AR coefficients, let's see how we can forecast a future value.
For this example, we are going to forecast the value of the 11th datapoint's value, based on the first 10 datapoints' values. We'll keep using the same sin wave.
// The sin wave
var t = new ts.main(ts.adapter.sin({cycles:4}));
// We're going to forecast the 11th datapoint
var forecastDatapoint = 11;
// We calculate the AR coefficients of the 10 previous points
var coeffs = t.ARMaxEntropy({
data: t.data.slice(0,10)
});
// Output the coefficients to the console
console.log(coeffs);
// Now, we calculate the forecasted value of that 11th datapoint using the AR coefficients:
var forecast = 0; // Init the value at 0.
for (var i=0;i<coeffs.length;i++) { // Loop through the coefficients
forecast -= t.data[10-i][1]*coeffs[i];
// Explanation for that line:
// t.data contains the current dataset, which is in the format [ [date, value], [date,value], ... ]
// For each coefficient, we substract from "forecast" the value of the "N - x" datapoint's value, multiplicated by the coefficient, where N is the last known datapoint value, and x is the coefficient's index.
}
console.log("forecast",forecast);
// Output: 92.7237232432106
Based on the value of the first 10 datapoints of the sin wave, out forecast indicates the 11th value should be around 92.72 so let's check that visually. I've re-generated the same sin wave, adding a red dot on the 11th point:
As we can see on the chart, the 11th datapoint's value seems to be around 92, as was forecasted.
We can also use regression_forecast method, which will using regression to forecast n datapoints based on defined sample from dataset. For resulting forecast datapoint same as above, we will first define the options:
var options = {
n: 1, // How many data points to be forecasted
sample: 10, // How many datapoints to be training dataset
start: 11, // Initial forecasting position
// method: "ARMaxEntropy", // What method for forecasting
// degree: 5, // How many degree for forecasting
// growthSampleMode: false, // Is the sample use only last x data points or up to entire data points?
}
Now, we generate the regression forecast on the data, then it resulted the MSE & trained data:
var MSE = t.regression_forecast(options)
console.log(MSE) // 0.000022902164211893183
console.log(t.data[10][1]) // 93.97404769915791
Based on the value of the first 10 datapoints of the sin wave, out forecast indicates the 11th value is 93.97404769915791. This interesting because the 11th observed real datapoint value is 93.96926207859084, which means it seems as was forecasted.
In order to check the forecast accuracy on more complex data, you can access the sliding_regression_forecast method, which will use a sliding window to forecast all of the datapoints in your dataset, one by one. You can then chart this forecast and compare it t the original data.
First, let's generate a dataset that is a little bit more complex data than a regular sin wave. We'll increase the sin wave's frequency over time using the inertia parameter to control the increase:
var t = new ts.main(ts.adapter.sin({cycles:10, inertia:0.2}));
Now, we generate the sliding window forecast on the data, and chart the results:
// Our sin wave with its frequency increase
var t = new ts.main(ts.adapter.sin({cycles:10, inertia:0.2}));
// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)
// The default method used is Max Entropy
t.sliding_regression_forecast({sample:20, degree: 5});
// Now we chart the results, comparing the the original data.
// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:
var chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});
And here is the result:
- The red line is the original data.
- The blue line is the forecasted data.
- The red dot indicate at which point the forecast starts.
Despite the frequency rising with time, the forecast is still pretty accurate. For the first 2 cycles, we can barely see the difference between the original data and the forecasted data.
Now, let's try on a more complex data.
Wee're going to generate a dataset using 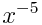
var t = new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));
Now we forecast the same way we did in the previous example on the sin wave:
var t = new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));
// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)
// The default method used is Max Entropy
t.sliding_regression_forecast({sample:20, degree: 5});
// Now we chart the results, comparing the the original data.
// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:
var chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});
Now let's try the same thing, using the Least Square method rather than the default Max Entropy method:
var t = new ts.main(ts.adapter.complex({cycles:10, inertia:0.1}));
// We are going to use the past 20 datapoints to predict the n+1 value, with an AR degree of 5 (default)
// The default method used is Max Entropy
t.sliding_regression_forecast({sample:20, degree: 5, method: 'ARLeastSquare'});
// Now we chart the results, comparing the the original data.
// Since we are using the past 20 datapoints to predict the next one, the forecasting only start at datapoint #21. To show that on the chart, we are displaying a red dot at the #21st datapoint:
var chart_url = t.chart({main:true,points:[{color:'ff0000',point:21,serie:0}]});
Now, let's try the forecasting on real data, using the stock price of Facebook ($FB):
// We fetch the financial data from MongoDB, then use adapter.fromDB() to load that data
var t = new ts.main(ts.adapter.fromDB(financial_data));
// Now we remove the noise from the data and save that noiseless data so we can display it on the chart
t.smoother({period:4}).save('smoothed');
// Now that the data is without noise, we use the sliding window forecasting
t.sliding_regression_forecast({sample:20, degree: 5});
/ Now we chart the data, including the original financial data (purple), the noiseless data (pink), and the forecast (blue)
var chart_url = t.chart({main:true,points:[{color:'ff0000',point:20,serie:0}]});
Exploring which degree to use, which method to use (Least Square or Max Entropy) and which sample size to use is time consumming, and you might not find the best settings by yourself.
Thats why there is a method that will incrementally search for the best settings, that will lead to the lowest MSE.
We'll use the $FB chart again, with its noise removed.
// We fetch the financial data from MongoDB, then use adapter.fromDB() to load that data
var t = new ts.main(ts.adapter.fromDB(financial_data));
// Now we remove the noise from the data and save that noiseless data so we can display it on the chart
t.smoother({period:4}).save('smoothed');
// Find the best settings for the forecasting:
var bestSettings = t.regression_forecast_optimize(); // returns { MSE: 0.05086675645862624, method: 'ARMaxEntropy', degree: 4, sample: 20 }
// Apply those settings to forecast the n+1 value
t.sliding_regression_forecast({
sample: bestSettings.sample,
degree: bestSettings.degree,
method: bestSettings.method
});
// Chart the data, with a red dot where the forecasting starts
var chart_url = t.chart({main:false,points:[{color:'ff0000',point:bestSettings.sample,serie:0}]});
MIT