The solution based on the vehicle routing problem is in this repository described in python by me in notebook format.
Click here to read my article about it on Medium: Desmistificando roteirizações com Python
Jupyter Notebook
1 - For you to run the notebook, you need to have Jupyter installed on your computer or access it in the cloud.
2 - You also need to create a Mapbox account to get the token so you can plot the clustered routes on the map
In the notebook put your token in the following variable
mapbox_token = <Your_Token>3 - You need to have installed the following packages
3 - Just run It
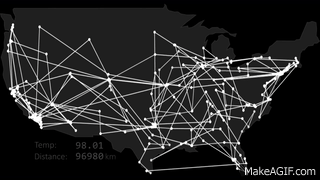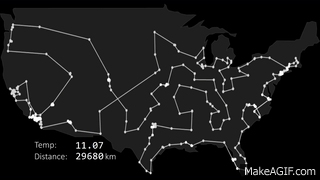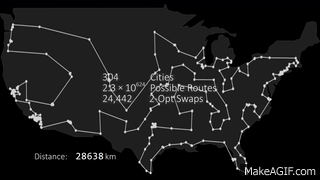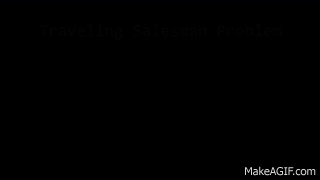
I used in the implementation as a reference all the US states as visiting points, the spreadsheet with the data is in the project.
Further explanations about the implementation can be found in the notebook
One of the most famous and well-known problems in the areas of computer science and operations research is the traveling salesman problem (TSP) which consists of: Given a set of cities and their positions, the problem is to find the shortest route for each city be visited only once and finally return to the starting point.
The problem can be solved by analyzing each round-trip route to determine the shortest. However, as the number of destinations increases, the corresponding number of round trips exceeds the capabilities of even the fastest computers. With 10 destinations, there can be over 300,000 permutations and round-trip combinations. With 15 destinations, the number of possible routes could exceed 87 billion.
In the Vehicle Routing Problem (VRP), the objective is to find optimal routes for multiple vehicles visiting a set of locations. (When there is only one vehicle, it boils down to the Traveling Salesman Problem.)
Vehicle routing problems are inherently intractable: the time required to resolve them grows exponentially with the size of the problem.
But what do we mean by "optimal routes" for a VRP? One answer is the routes with the shortest total distance. However, if there are no other restrictions, the ideal solution is to assign only one vehicle to visit all locations and find the shortest route for that vehicle. This is essentially the same problem as TSP.
A better way to define optimal routes is to minimize the length of the longest single route among all vehicles. This is the right definition if the goal is to complete all deliveries as quickly as possible.