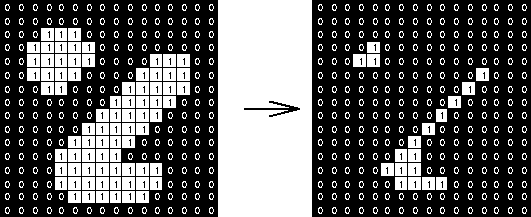========
The purpose of morph.js is to make the low level image processing and computer vision functions defined by mathematical morphology available for use with preproccessed input from the webcam via window.getUserMedia(). Morph.js deals with binary images, in other words, all operations are done on arrays of ones and zeroes.
Mathematical morphology (MM) is a theory and technique for the analysis and processing of geometrical structures, based on set theory, lattice theory, topology, and random functions. MM is most commonly applied to digital images, but it can be employed as well on graphs, surface meshes, solids, and many other spatial structures. Topological and geometrical continuous-space concepts such as size, shape, convexity, connectivity, and geodesic distance, were introduced by MM on both continuous and discrete spaces. MM is also the foundation of morphological image processing, which consists of a set of operators that transform images according to the above characterizations. MM was originally developed for binary images, and was later extended to grayscale functions and images. The subsequent generalization to complete lattices is widely accepted today as MM's theoretical foundation.
To initialize a morph object:
var height = 200
var width = 270
var morph = new Morph(height, width, bits)
where bits is an array of 1s and 0s with length (height * width), usually derived from some image.
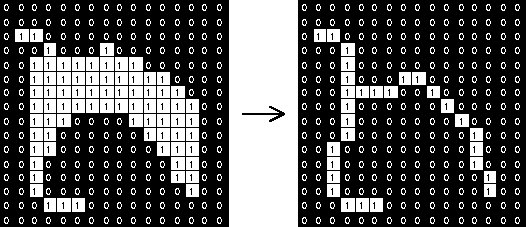
Basic functionality in Morphological image processing (MIP) is defined by the erode and dilate operations.
morph.erodeWithElement()
when no structuring element argument is provided all operations default to using a default 3x3 rectangular structuring element that looks like this:
[1,1,1,
1,1,1,
1,1,1]
And will provide results like this:
Users can select from other predefined structuring elements like MORPH_3x3_CROSS_ELEMENT, or define their own structuring elements:
var el = new StructuringElement(3,[1,1,1,
0,1,0,
0,0,0])
Where the 1st argument is the dimension of the element.
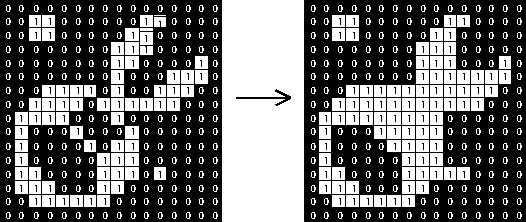
morph.dilateWithElement()
Will provide results like this:
Example usage: http://somatostat.in/swarmSandbox.html
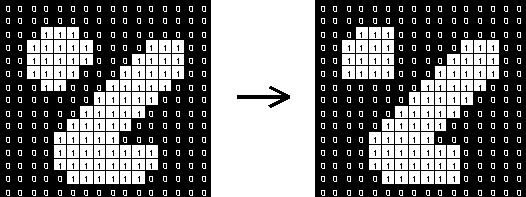
In image processing, closing is, together with opening, the basic workhorse of morphological noise removal. Opening removes small objects, while closing removes small holes [wikipedia].
morph.closingWithElement()
Closing is the dilation operation followed by the erosion operation and depending on the structuring elements used, gives an effect similar to below.
morph.openingWithElement()
effect:
removing a small object with opening:
The hit-miss transform can be described as a very simplistic corner detector. In morph.js you cannot specify the structuring elements used in the hit-miss transform.
morph.hitMissTransform()
Here is the effect:
Thinning is the act of iteratively subtracting the hit miss transform from the image it was generated from.
var iterations = 6;
morph.iterativeThinning(iterations);
If you set the parameter high enough then it will eventually converge to the 'skeletonization' of the image, shown below.
Be aware: the time complexity of reaching a complete skeletonization is prohibitive for most real-time processing applications.
var componentData = morph.labelConnectedComponents()
componentData.contours.forEach(function(contour){
console.log(contour)
// returns an array of normalized x,y values [ [0.1,0.2], [0.8,0.1], .... ]
})
This is (in my opinion) the most useful algo in morph.js. Given a binary image, it will label connected sections with integers (not neccesarily consecutive). It is an implementation of the "two pass" algorithm described on wikipedia (http://en.wikipedia.org/wiki/Connected-component_labeling), and labels regions that are "8-connected". It is also relatively speedy, running linearly wrt the number of pixels. Using the connected component data you can color a bitmap image like this:
For more info about morphological image proccessing, check out this site, which I referenced extensively above: http://homepages.inf.ed.ac.uk/rbf/HIPR2/morops.htm