Metallurgy

The Metallurgy package enables calculation of approximate properties of alloy mixtures, based on the linear mixture of elemental properties.

Installation

The metallurgy package can be installed from pypi using pip:

pip install metallurgy

Usage

Alloys

Most of the features of metallurgy are based on the concept of an alloy, a mixture of elements:

import metallurgy as mg

Bronze = mg.Alloy("Cu88Sn12")

An alloy can be defined in several ways:

>>> mg.Alloy("Cu50Zr50")
Cu50Zr50

>>> mg.Alloy("CuZr")
Cu50Zr50

>>> mg.Alloy("CuZrFeCo")
Cu25Zr25Fe25Co25

>>> mg.Alloy("(Fe70Co30)50Ni50")
Ni50Fe35Co15

>>> mg.Alloy("(FeCo)50Ni50")
Ni50Fe25Co25

>>> mg.Alloy({"Pt": 30, "Al": 45, "Ag": 25})
Al45Pt30Ag25

While formally, an alloy is defined as "a mixture of chemical elements of which at least one is a metal", no such limitation is enforced in this package -- you can create any mixture you want.

An Alloy object has access to properties containing the percentage values of the composition, the elements in the composition, and has helper functions which can convert the composition to a simple string or even a LaTeX formatted string:

>>> Bronze.composition
{'Cu': 0.88, 'Sn': 0.12}

>>> Bronze.elements
['Cu', 'Sn']

>>> Bronze.to_string()
'Cu88Sn12'

>>> Bronze.to_pretty_string()
'Cu$_{88}$Sn$_{12}$'

Calculating alloy properties

Properties of alloys may be approximated from the properties of their constituent elements via the linear mixture rule:

$$\Sigma A = \sum_{i=1}^{N} c_i A_i $$

where $\Sigma A$ is the approximate mixed value of a property $A$ for an alloy that contains $N$ elements with percentages $c_i$. Similarly, the deviation of these elemental property values for the elements present in an alloy can be calculated:

$$\delta A = \sqrt{\sum_{i=1}^{N} c_i \left(1 - \frac{A_i}{\Sigma A}\right)^2} $$

The metallurgy package can be used to calculate a variety of approximate alloy properties:

Bronze = mg.Alloy("Cu88Sn12")

>>> mg.linear_mixture(Bronze, "mass")
70.16568

>>> mg.linear_mixture(Bronze, "density")
8.7566

>>> mg.linear_mixture(Bronze, "valence")
2.24

>>> mg.deviation(Bronze, "mass")
17.926178182133523

>>> mg.deviation(Bronze, "density")
0.5508098038343185

>>> mg.deviation(Bronze, "valence")
0.6499230723708769

Elemental data is provided by the elementy package. Metallurgy can calculate a variety of other alloy properties that are more complex than simple linear mixture or deviations of elemental properties:

>>> mg.enthalpy.mixing_Gibbs_free_energy(Bronze)
-2039.0961905675026

>>> mg.entropy.ideal_entropy(Bronze)
0.3669249912727096

>>> mg.density.theoretical_density(Bronze)
8.554783679490685

>>> mg.valence.d_valence(Bronze)
0.8661417322834646

See our June 2022 paper "Machine-learning improves understanding of glass formation in metallic systems" that used code which later became the metallurgy package for definitions of these alloy properties.

Generating alloy datasets

Metallurgy can also be used to generate collections of alloys, either randomly or across a composition-space.

>>> mg.generate.binary(["Fe", "Co"], step=10)
[Fe100, Fe90Co10, Fe80Co20, Fe70Co30, Fe60Co40,
Fe50Co50, Co60Fe40, Co70Fe30, Co80Fe20, Co90Fe10, Co100]

>>> mg.generate.ternary(["Fe", "Co", "Al"], step=20)
[Fe100, Fe80Co20, Fe80Al20, Fe60Co40, Fe60Co20Al20,
Fe60Al40, Co60Fe40, Fe40Co40Al20, Fe40Al40Co20, Al60Fe40,
Co80Fe20, Co60Fe20Al20, Co40Al40Fe20, Al60Fe20Co20,
Al80Fe20, Co100, Co80Al20, Co60Al40, Al60Co40, Al80Co20, Al100]

>>> mg.generate.random_alloy()
Cs28.9Db25.4Hs12Ce11.9La10.6Cu9.6Kr1.6

>>> mg.generate.random_alloy()
Ba94.5Y5.5

We can apply constraints to the randomly generated alloy, such as limits on the maximum and minimum number of constituent elements, requirements on the percentage range that particular elements must be within, and whitelists of allowed elements:

>>> mg.generate.random_alloy(min_elements=2, max_elements=3)
Au50.7Hf36.3Ru13

>>> mg.generate.random_alloy(min_elements=2, max_elements=3, percentage_constraints={"Cu":{"min":0.3, "max":0.8}})
Cu63.9Sr23.9Be12.2

>>> mg.generate.random_alloy(min_elements=2, max_elements=3, percentage_constraints={"Cu":{"min":0.3, "max":0.8}}, allowed_elements=["Fe", "Cu", "Co", "Ni", "Yb"])
Yb64.8Cu30Ni5.2

The process of generating random alloys can be performed in bulk to create datasets of random alloys:

>>> mg.generate.random_alloys(10, min_elements=2, max_elements=3)
[Fl94.6Xe5.4, Po64.2Tl23.3Np12.5, Tb61.6Ta38.4, Lu50.8Ho38.1In11.1, Rn69Es31, S70.4Ts29.6, Pr79.3He13.4Cm7.3, As84.3V15.7, Ge45.3Xe41.2Na13.5, Ra70.4He29.6]

Plotting alloy information

Once you have created a dataset of alloys, you may wish to view graphically a particular material property on a population level:

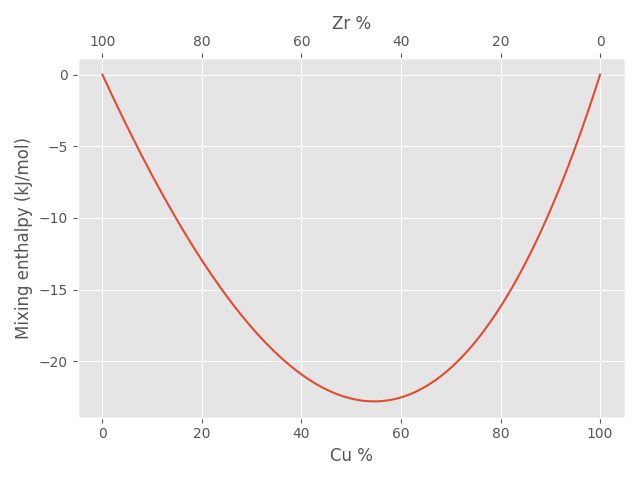
>>> binary, percentages = mg.generate.binary(["Cu", "Zr"])
>>> mixing_enthalpies = mg.enthalpy.mixing_enthalpy(binary)
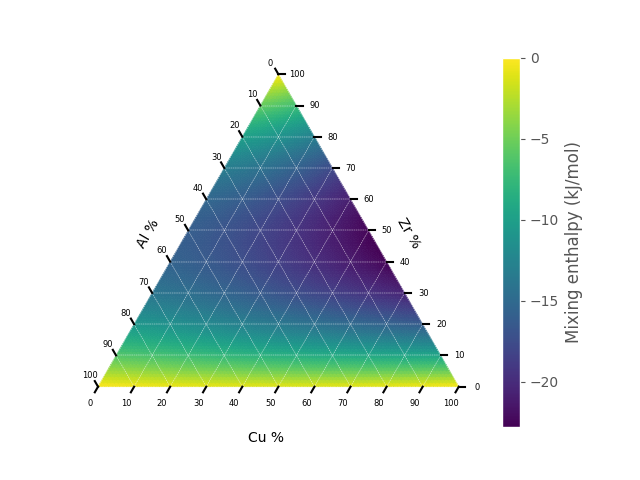
>>> mg.plots.binary(binary, mixing_enthalpies, ylabel="Mixing enthalpy (kJ/mol)")

>>> ternary, percentages = mg.generate.ternary(["Cu", "Zr", "Al"])
>>> mixing_enthalpies = mg.enthalpy.mixing_enthalpy(ternary)
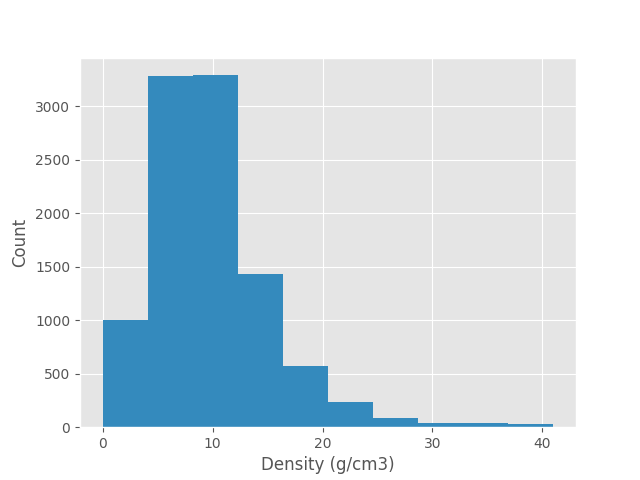
>>> mg.plots.ternary(ternary, mixing_enthalpies, label="Mixing enthalpy (kJ/mol)")

>>> import matplotlib.pyplot as plt
>>> alloys = mg.generate.random_alloys(10000)
>>> plt.hist(mg.linear_mixture(alloys, "density"))

Documentation

Documentation is available here.