Note
To circumvent the GitHub Git LFS limit, both the data and model weights have been relocated to Google Drive. To replicate our repository, please download these files and place them in the appropriate directories.
Convolution operation
(Source: towardsdatascience.com)
(Source: towardsdatascience.com)
- 1. Introduction
- 2.Augmentation techniques
- 3. CNNs
- 4. Random Search
- 5. Training Procedure
- 6. Pre-training & Fine-tuning
- 7. Evaluation & Extension
- 8. Project Structure
The EMNIST dataset is a set of handwritten character digits derived from the NIST Special Database 19 and converted to a 28x28 pixel image format and dataset structure that directly matches the MNIST dataset. Further information on the dataset contents and conversion process can be found in the paper available at EMNIST: an extension of MNIST to handwritten letters.
There are six different splits provided in this dataset. A short summary of the dataset is provided below:
EMNIST ByClass: 814,255 characters. 62 unbalanced classes.
EMNIST ByMerge: 814,255 characters. 47 unbalanced classes.
EMNIST Balanced: 131,600 characters. 47 balanced classes.
EMNIST Letters: 145,600 characters. 26 balanced classes.
EMNIST Digits: 280,000 characters. 10 balanced classes.
EMNIST MNIST: 70,000 characters. 10 balanced classes.
Note: The dataset used has been bolded.
The full complement of the NIST Special Database 19 is available in the ByClass and ByMerge splits. The EMNIST Balanced dataset contains a set of characters with an equal number of samples per class. The EMNIST Letters dataset merges a balanced set of uppercase and lowercase letters into a single 26-class task. The EMNIST Digits and EMNIST MNIST datasets provide balanced handwritten digit datasets directly compatible with the original MNIST dataset.
Augmentation techniques referenced Stochastic optimization of plain convolutional neural networks with simplemethods.
In details, they are:
class AugmentDataset(Dataset):
def __init__(self, images, labels, augment):
self.images = images
self.labels = labels
# Define the data augmentation of images
self.transform = augment
def __len__(self):
return len(self.images)
def __getitem__(self, idx):
img = self.images[idx]
lab = self.labels[idx]
if self.transform:
img = self.transform(img)
return img, lab
# A combination of five data augmentation techniques,
# including rotation, shearing, shifting up and down, zooming, and rescale
augment = transforms.Compose([
transforms.RandomAffine(degrees=15, translate=(0.1, 0.1), scale=(0.9, 1.1), shear=3),
transforms.ToTensor(),
transforms.Normalize((mean, ), (std, )) # mean, std = 0.1736, 0.3248
])
Effects of augmentation techniques
Before choosing architectures, we referred to the MNIST leaderboard.
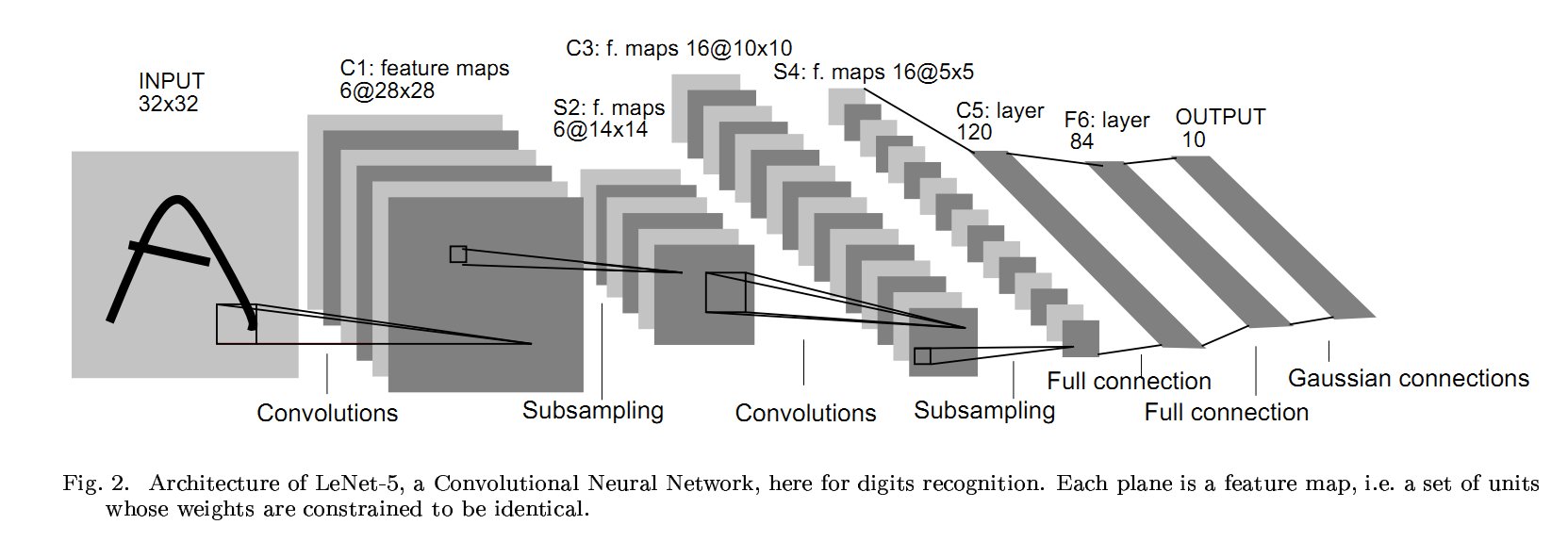
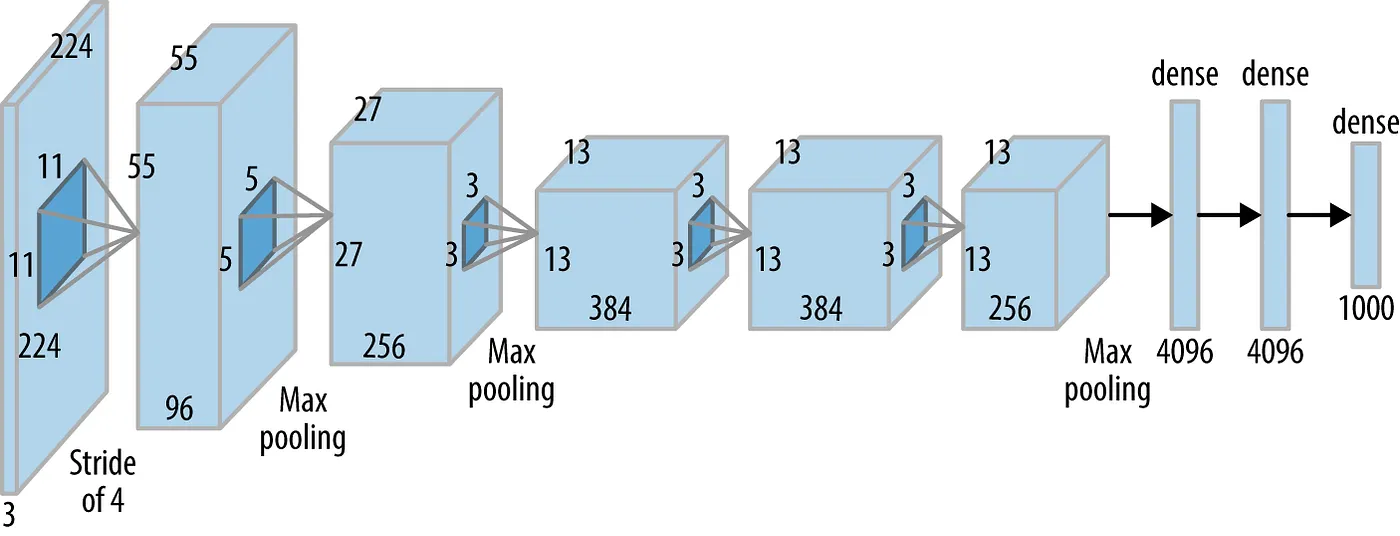
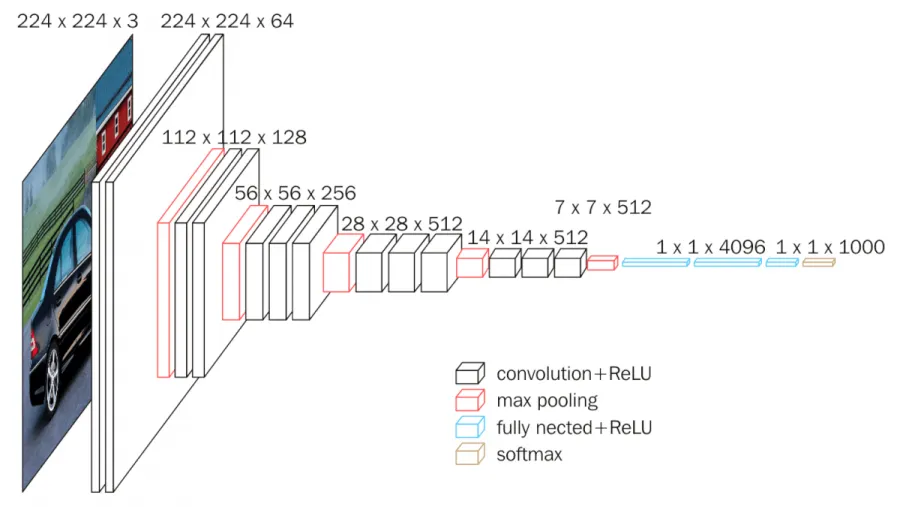
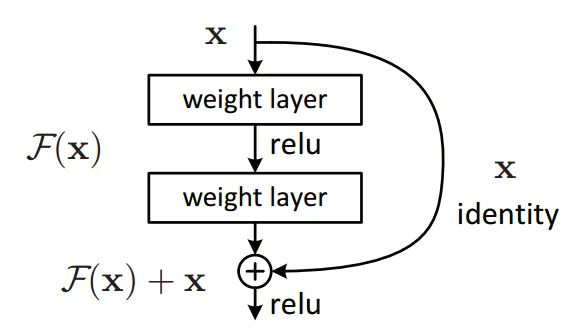
In this experiment, six different CNNs have been reproduced and modified.
LeNet-5
(Source: gamedevacademy.org)
(Source: gamedevacademy.org)
# A varient of LeNet
class LeNet(nn.Module):
def __init__(self, num_classes=62):
super(LeNet, self).__init__()
# Extract features
self.features = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2)
)
# Average pooling
self.avgpool = nn.AdaptiveAvgPool2d((3, 3))
# Feature classifier
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(16 * 3 * 3, 120),
nn.BatchNorm1d(120),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(120, 84),
nn.BatchNorm1d(84),
nn.ReLU(inplace=True),
nn.Linear(84, num_classes)
)
self._initialize_weights()
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
# Initialise the weights
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
# Kaiming normalisation
init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
init.constant_(m.weight, 1)
init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
init.normal_(m.weight, 0, 0.01)
init.constant_(m.bias, 0)
AlexNet
(Source: towardsdatascience.com)
(Source: towardsdatascience.com)
# A variant of AlexNet
class AlexNet(nn.Module):
def __init__(self, num_classes=62):
super(AlexNet, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=3, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(16, 48, kernel_size=3, padding=2),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Conv2d(48, 96, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(96, 64, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2),
)
self.avgpool = nn.AdaptiveAvgPool2d((3, 3))
self.classifier = nn.Sequential(
nn.Dropout(),
nn.Linear(64 * 3 * 3, 1024),
nn.BatchNorm1d(1024),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(1024, 1024),
nn.BatchNorm1d(1024),
nn.ReLU(inplace=True),
nn.Linear(1024, num_classes),
)
self._initialize_weights()
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
init.constant_(m.weight, 1)
init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
init.normal_(m.weight, 0, 0.01)
init.constant_(m.bias, 0)
VGGNet-16
(Source: towardsdatascience.com)
(Source: towardsdatascience.com)
# A variant of VGGNet
class VGGNet(nn.Module):
def __init__(self, num_classes=62):
super(VGGNet, self).__init__()
self.features = nn.Sequential(
# Block 1
nn.Conv2d(1, 16, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
# Block 2
nn.Conv2d(16, 32, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 3
nn.Conv2d(32, 64, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(64, 64, kernel_size=3, padding=1),
nn.ReLU(inplace=True),
# Block 4
nn.Conv2d(64, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 5
nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
nn.Conv2d(128, 128, kernel_size=3, stride=1, padding=1),
nn.ReLU(inplace=True),
)
self.avgpool = nn.AdaptiveAvgPool2d((3, 3))
self.classifier = nn.Sequential(
nn.Linear(128 * 3 * 3, 512),
nn.BatchNorm1d(512),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(512, 512),
nn.BatchNorm1d(512),
nn.ReLU(inplace=True),
nn.Dropout(),
nn.Linear(512, num_classes),
)
self._initialize_weights()
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x = self.classifier(x)
return x
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
init.constant_(m.weight, 1)
init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
init.normal_(m.weight, 0, 0.01)
init.constant_(m.bias, 0)
Single Residual Block
(Source: towardsdatascience.com)
(Source: towardsdatascience.com)
# A variant of ResNet
class BasicBlock(nn.Module):
def __init__(self, in_channels, out_channels, stride=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(in_channels, out_channels, kernel_size=3, stride=stride, padding=1, bias=False)
self.bn1 = nn.BatchNorm2d(out_channels)
self.conv2 = nn.Conv2d(out_channels, out_channels, kernel_size=3, stride=1, padding=1, bias=False)
self.bn2 = nn.BatchNorm2d(out_channels)
self.shortcut = nn.Sequential()
if stride != 1 or in_channels != out_channels:
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=stride, bias=False),
nn.BatchNorm2d(out_channels)
)
def forward(self, x):
out = nn.ReLU(inplace=True)(self.bn1(self.conv1(x)))
out = self.bn2(self.conv2(out))
out += self.shortcut(x)
out = nn.ReLU(inplace=True)(out)
return out
class ResNet(nn.Module):
def __init__(self, num_classes=62):
super(ResNet, self).__init__()
self.in_channels = 16
self.model = nn.Sequential(
nn.Conv2d(1, 16, kernel_size=3, stride=1, padding=1, bias=False),
nn.BatchNorm2d(16),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
self._make_layer(16, 2, stride=1),
self._make_layer(32, 2, stride=2),
self._make_layer(64, 2, stride=2),
self._make_layer(128, 2, stride=2),
nn.AdaptiveAvgPool2d((1, 1)),
nn.Flatten(start_dim=1),
nn.Linear(128, num_classes)
)
self._initialize_weights()
def _make_layer(self, out_channels, num_blocks, stride):
strides = [stride] + [1] * (num_blocks - 1)
layers = []
for stride in strides:
layers.append(BasicBlock(self.in_channels, out_channels, stride))
self.in_channels = out_channels
return nn.Sequential(*layers)
def forward(self, x):
return self.model(x)
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
nn.init.constant_(m.bias, 0)
SpinalNet Motivation
(Source: github.com/dipuk0506/SpinalNet)
(Source: github.com/dipuk0506/SpinalNet)
# A variant of SpinalNet
class SpinalNet(nn.Module):
def __init__(self, num_classes=62):
super(SpinalNet, self).__init__()
self.features = nn.Sequential(
# Block 1
nn.Conv2d(1, 32, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(32),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
# Block 2
nn.Conv2d(32, 64, kernel_size=5, stride=1, padding=2),
nn.BatchNorm2d(64),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.spinal_layer1 = nn.Linear(7 * 7 * 64 // 2, 50)
self.spinal_layer2 = nn.Linear(7 * 7 * 64 // 2 + 50, 50)
self.spinal_layer3 = nn.Linear(7 * 7 * 64 // 2 + 50, 50)
self.spinal_layer4 = nn.Linear(7 * 7 * 64 // 2 + 50, 50)
self.classifier = nn.Linear(50 * 4, num_classes)
self._initialize_weights()
def _initialize_weights(self):
for m in self.modules():
if isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
if m.bias is not None:
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.BatchNorm2d):
nn.init.constant_(m.weight, 1)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Linear):
nn.init.normal_(m.weight, 0, 0.01)
nn.init.constant_(m.bias, 0)
def forward(self, x):
x = self.features(x)
x = x.reshape(x.size(0), -1)
x1 = F.dropout(F.relu(self.spinal_layer1(x[:, :7 * 7 * 64 // 2])), training=self.training)
x2 = F.dropout(F.relu(self.spinal_layer2(torch.cat([x[:, 7 * 7 * 64 // 2:], x1], dim=1))), training=self.training)
x3 = F.dropout(F.relu(self.spinal_layer3(torch.cat([x[:, :7 * 7 * 64 // 2], x2], dim=1))), training=self.training)
x4 = F.dropout(F.relu(self.spinal_layer4(torch.cat([x[:, 7 * 7 * 64 // 2:], x3], dim=1))), training=self.training)
x = torch.cat([x1, x2, x3, x4], dim=1)
x = self.classifier(x)
return x# A variant of EnsNet
class EnsNet(nn.Module):
def __init__(self, num_classes=62):
super(EnsNet, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=3, padding=1),
nn.BatchNorm2d(64),
nn.ReLU(inplace=True),
nn.Dropout(0.35),
nn.Conv2d(64, 128, kernel_size=3),
nn.BatchNorm2d(128),
nn.ReLU(inplace=True),
nn.Dropout(0.35),
nn.Conv2d(128, 256, 3, padding=1),
nn.BatchNorm2d(256),
nn.ReLU(inplace=True),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Dropout(0.35),
nn.Conv2d(256, 512, kernel_size=3, padding=1),
nn.BatchNorm2d(512),
nn.ReLU(inplace=True),
nn.Dropout(0.35),
nn.Conv2d(512, 1024, kernel_size=3),
nn.BatchNorm2d(1024),
nn.ReLU(inplace=True),
nn.Dropout(0.35),
nn.Conv2d(1024, 2000, 3, padding=1),
nn.BatchNorm2d(2000),
nn.ReLU(inplace=True),
nn.MaxPool2d(2, 2),
nn.Dropout(0.35),
)
self.avgpool = nn.AdaptiveAvgPool2d((3, 3))
self.classifier_major = nn.Linear(200 * 3 * 3, num_classes)
self.classifiers = nn.ModuleList([
nn.Linear(200 * 3 * 3, num_classes)
for _ in range(10)
])
self.weights = nn.Parameter(torch.ones(11) / 11, requires_grad=True)
def forward(self, x):
x = self.features(x)
x = self.avgpool(x)
x = torch.flatten(x, 1)
x_major = self.classifier_major(x[:, :200 * 3 * 3])
x_rest = [classifier(x[:, 200 * i * 3 * 3:200 * (i + 1) * 3 * 3]) for i, classifier in enumerate(self.classifiers)]
all_x = torch.stack([x_major] + x_rest, dim=1)
weighted_x = torch.sum(all_x * self.weights.view(1, -1, 1), dim=1)
return weighted_x# Define a general hyperparameter search space for most of our models, except for ResNet
param_grid = {
'learning_rate': [1e-3, 1e-2, 1e-1], # Learning rate, one of the most important hyperparameters in machine learning and deep learning;
'batch_size': [16, 32, 64], # Batch size, another crucial hyperparameter related to training efficiency and quality;
'momentum': [0, 0.85, 0.9, 0.95], # Momentum, a hyperparameter of SGD, which is used to accelerate the convergence speed;
'weight_decay': [0, 1e-2, 1e-3, 1e-4] # Weight decay, a hyperparameter for L2 regularization to avoid overfitting.
}
def train_and_evaluate(model, optimizer, criterion, train_loader, val_loader, num_epochs):
'''Compute the validation loss during the training epochs'''
"""Parameters:
model, corresponds to a specific classifier;
optimizer, corresponds to a PyTorch optimizer, typically SGD and Adam;
criterion, corresponds to Cross Entropy Loss in our context;
train_loader, corresponds to a PyTorch DataLoader containing training inputs and labels;
valid_loader, corresponds to a PyTorch DataLoader containing validation inputs and labels;
num_epochs, correspond to the number of training epochs.
Return:
val_loss, the loss value on the validation set during the specific training procedure.
"""
# Switch the model to the training state
model.train()
# Train model for several epochs
for epoch in range(num_epochs):
for inputs, targets in train_loader:
optimizer.zero_grad()
outputs = model(inputs)
loss = criterion(outputs, targets)
loss.backward()
optimizer.step()
# Switch the model to the evaluation state
model.eval()
# Compute the loss value on the validation set
val_loss = 0
with torch.no_grad():
for inputs, targets in val_loader:
outputs = model(inputs)
loss = criterion(outputs, targets)
val_loss += loss.item()
val_loss /= len(val_loader)
return val_loss
def random_search(model_class, param_grid, n_iter=28, num_epochs=5):
'''Random search algorithm to find the locally optimal combination of hyperparameters.'''
""" Parameters:
model_class, corresponds to a specific model class, instead of an initialized model;
param_grid, corresponds to the hyperparameter search space;
n_iter, corresponds to the number of iterations for hyperparameter tuning, Default: 28 because it is 20% of the size of our general hyperparameter search space;
num_epochs, corresponds to the number of training epochs, Default: 5. For hyperparameter tuning, 20 epochs are usually enough.
Return:
best_param, corresponds to a Python dictionary which contains the specific hyperparameter's name and its optimal option.
"""
# Convert the hyperparameter search space from a Python dictionary to a Python list in order to sample them randomly
param_list = list(ParameterSampler(param_grid, n_iter))
best_loss = float('inf')
best_params = None
criterion = nn.CrossEntropyLoss()
# Use a Python set to avoid repeated combinations
params_attempt = set()
for params in tqdm(param_list):
params_tuple = tuple(params.items())
if params_tuple in params_attempt:
continue
else:
params_attempt.add(params_tuple)
# Initialise a model
model = model_class()
# Optimizer containing 3 hyperparameters
optimizer = optim.SGD(model.parameters(),
lr=params['learning_rate'], momentum=params['momentum'], weight_decay=params['weight_decay'])
# DataLoader containing 1 hyperparameter 'batch_size' for hyperparameter tuning
train_loader_tuning = DataLoader(emnist_mini_train, batch_size=params['batch_size'], shuffle=True, num_workers=2)
val_loader_tuning = DataLoader(emnist_mini_val, batch_size=params['batch_size'], shuffle=True, num_workers=2)
# Compute the validation loss value based on the function we defined before
val_loss = train_and_evaluate(model, optimizer, criterion, train_loader_tuning, val_loader_tuning, num_epochs)
# Compare the loss value
if val_loss < best_loss:
best_loss = val_loss
best_params = params
return best_paramsDue to the limitations of computational resources, we utilized a subset of the full dataset for training, comprising 120,000 images, which represents approximately 14% of the entire dataset.
The training procedure of VGGNet is shown below:
Training procedure of VGGNet
The main difference between pre-training and fine-tuning in this experiment is:
- Pre-training:
- Optimizer: SGD
- Proportion of the training data: 90%
- Fine-tuning:
- Optimizer: Adam
- Proportion of the training data: 100%
def evaluate(model, data_loader):
'''Model performance, including accuracy, precision, recall, F1-score, and confusion matrix'''
""" Parameters:
model, corresponds to
data_loader, corresponds to the specific PyTorch DataLoader,
If we want to evaluate the performance of the training set, we can use the DataLoader of the training dataset;
If we want to evaluate the performance of the test set, we can use the DataLoader of the test dataset.
Returns:
acc, corresponds to the accuracy of a model on the specific dataset;
precision, corresponds to the precision of a model on the specific dataset;
recall, corresponds to the recall of a model on the specific dataset;
f1, corresponds to the F1 score of a model on the specific dataset;
cm, corresponds to the confusion matrix of the specific model on the specific dataset, which is in 2D ndarray format.
"""
# Swith the model to the evaluation state
model.eval()
all_preds = []
all_labels = []
# Compute the predicted labels
with torch.no_grad():
for images, labels in data_loader:
images, labels = images.float().to(device), labels.to(device)
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
all_preds.extend(predicted.cpu().numpy())
all_labels.extend(labels.cpu().numpy())
# Convert the data type from PyTorch Tensor to NumPy ndarray
all_preds = np.array(all_preds)
all_labels = np.array(all_labels)
# Compute different metrics
acc = accuracy_score(all_labels, all_preds)
precision = precision_score(all_labels, all_preds, average='weighted') # Consider unbalanced classes
recall = recall_score(all_labels, all_preds, average='weighted') # Consider unbalanced classes
f1 = f1_score(all_labels, all_preds, average='weighted') # Consider unbalanced classes
cm = confusion_matrix(all_labels, all_preds)
# Swith the model back to the training state if we want to keep training
model.train()
return acc, precision, recall, f1, cm
def confusion_matrix_viz(cm):
'''Visualise the confusion matrix'''
""" Parameter:
cm, corresponds to a confusion matrix in 2D ndarray format.
"""
# A label mapping
label_map = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz"
plt.figure(figsize=(40, 40))
sns.set(font_scale=1.5)
sns.heatmap(cm, annot=True, fmt='g', cmap='Blues', xticklabels=label_map, yticklabels=label_map)
plt.xlabel('Predicted Labels')
plt.ylabel('True Labels')
plt.show()| AlexNet | VGGNet | SpinalNet | ResNet | |
| Accuracy | 87.95% | 89.80% | 87.15% | 89.28% |
| Precision | 87.62% | 90.01% | 86.18% | 89.24% |
| Recall | 87.95% | 89.80% | 87.15% | 89.28% |
| F1 score | 86.59% | 88.42% | 85.28% | 88.30% |
| AlexNet | VGGNet | SpinalNet | ResNet | |
| Accuracy | 86.96% | 87.24% | 85.92% | 86.88% |
| Precision | 85.55% | 86.43% | 85.92% | 86.88% |
| Recall | 86.96% | 87.24% | 85.92% | 86.88% |
| F1 score | 85.58% | 85.66% | 84.07% | 85.68% |
- Performance on the entire dataset: 814,255 images
Predictions on random sampling characters
Confusion matrix on the training set
Confusion matrix on the test set
- Performance on the downstream task: MNIST
| Training | Test | |
| Accuracy | 95.24% | 95.27% |
| Precision | 95.26% | 95.27% |
| Recall | 95.24% | 95.27% |
| F1 score | 95.24% | 95.27% |
├── charclf
| ├── tools
| | ├── eval.py
| | ├── fine_tune.py
| | ├── train.py
| | ├── viz.py
| | └── __init__.py
| ├── dataset.py
| ├── models.py
| └── __init__.py
├── data
| ├── dataset_description.txt
| ├── emnist_test.pkl
| └── emnist_train.pkl
├── model_hub
| ├── pre_trained/
| │ └── {model_name}.pth
| └── fine_tuned/
| └── {model_name}_tuned.pth
├── outputs/
│ └── *.png
├── LICENSE
├── notebook.ipynb
├── README.md
└── requirements.txt