Egyptian Ale Jug Puzzle

From: "Tutanhkamun's Book of Puzzles" by Tim Dedopulus, 2013, Metro Book, ISBN 978-1-4351-4899-4

Problem 23, page 32 reads:

The Keeper of Ale found himself with a problem earlier. I suspect that you
would have been able to advise him properly, Great One. He found himeself with just
three jars. The largest, an 8 hinu jar, was full of ale. The two smaller jars,
measuring 5 hinu and 3 hinu, were both empty. He needed to prepare two four-hinu
measures of ale. What is the most effective way that he could do so without
resorting to guesswork or findind some extra measuring devices?

According to Wikipedia, this is the canonical version of the problem: 3 jugs, 8, 5 and 3 measures capacity respectively, with the 8-measure jug full at the start. How about that!?!

Implementation

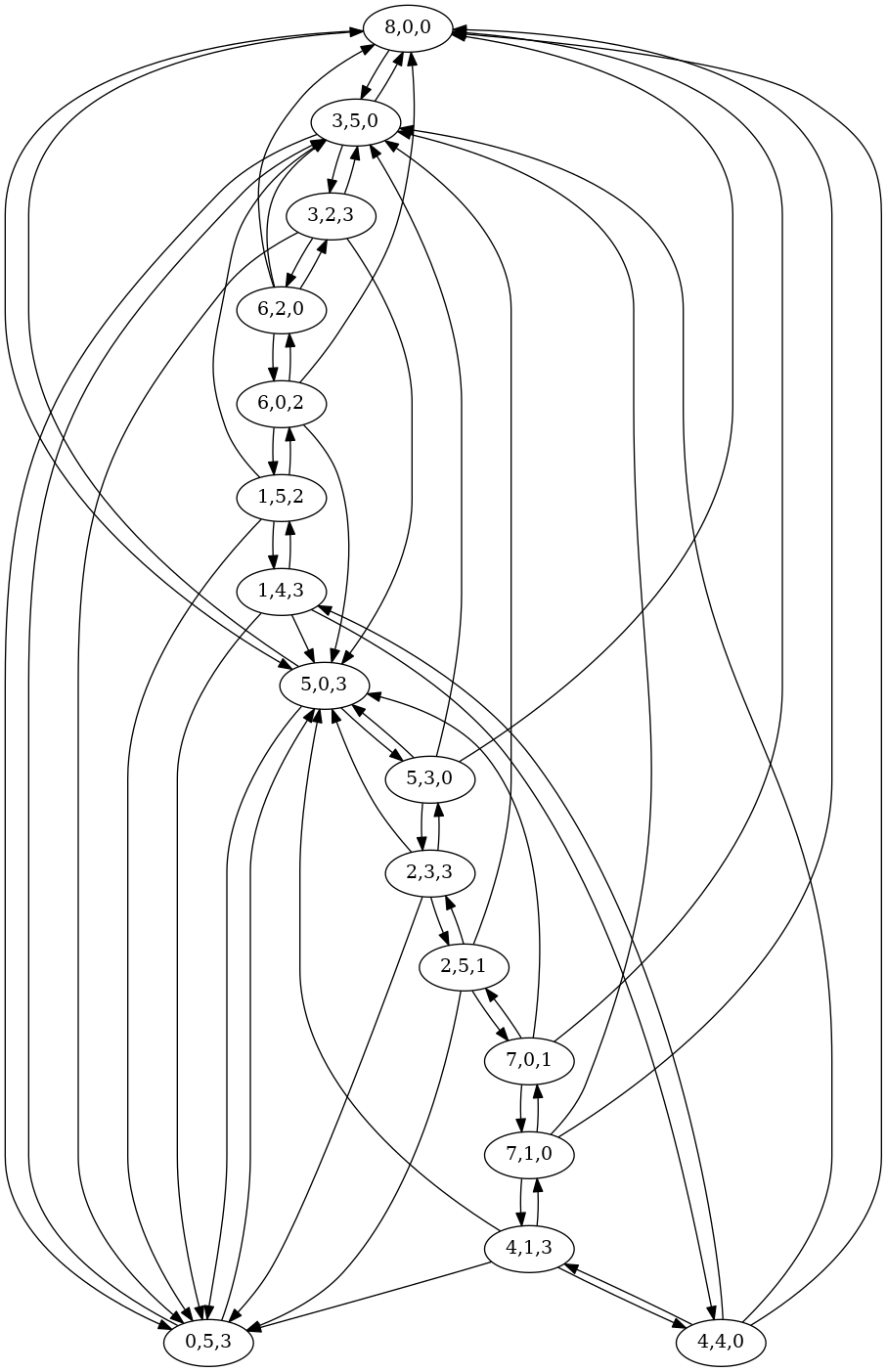
I wrote a small Python program to explore the entire state-space of the 3 jugs. Each state is a triplet of integers, like (8,0,0) or (0,5,3). Each triplet represents (in order) the amount of ale in the 8-hinu jug, the 5-hinu jug and the 3-hinu jug. Starting with (8,0,0), the program "pours" ale from an ale-containing jug into another jug, taking care not to "overflow" any particular jug. Each child triplet the program obtains gets pushed on a queue. For the (8,8,8) starting state, only child states (3,5,0) and '(5,0,3)` are possible.

When all child states have been created and enqueued, the program removes a triplet from the queue. Using the new triplet, it repeats the process of generating legal triplets. The program uses a Python dict object to keep track of any triplets for which it has generated child triplets. When the program removes a triplet from the queue, it checks the dict to ensure it hasn't examined this triplet before. So, if the state space of the jugs is finite, the program will eventually halt.

I made the python script (egypt) a little more general than the particular problem. You can set the starting state to whatever you'd like, as long as no jug overflows. I was not able to find a starting state that had an infinite state space, but some starting states, like (4,3,1) or (5,1,2), cannot be reached from the other states.

Solution

For the (8,0,0) starting triplet, the program finds a 16-state space with any number of cycles. No nodes are only "out" or "in" nodes, where you can only start at an "out" node and never get back, or arrive at an "in" node and never pour into another jug to reach a different triplet.

I make out the shortest path from (8,0,0) to (4,4,0) is:

1. (8,0,0) → (3,5,0) - fill the 5-hinu jar from the 8-hinu jar
2. (3,5,0) → (3,2,3) - fill the 3-hinu jar from the 5-hinu jar
3. (3,2,3) → (6,2,0) - pour the 3-hinu jar into the 8-hinu jar
4. (6,2,0) → (6,0,2) - pour the 5-hinu jar into the 3-hinu jar
5. (6,0,2) → (1,5,2) - fill the 5-hinu jar from the 8-hinu jar
6. (1,5,2) → (1,4,3) - fill the 3-hinu jar from the 5-hinu jar
7. (1,4,3) → (4,4,0) - pour the 3-hinu jar into the 8-hinu jar

This is different, and one step shorter, than the book's solution. I've written down the book's solution, annotated with its odd description.

1. (8,0,0) → (5,0,3) - Fill 3
2. (5,0,3) → (5,3,0) - put into 5
3. (5,3,0) → (2,3,3) - Fill 3 from 8
4. (2,3,3) → (2,5,1) - fill 5. The 8 now holds two, the 5 holds 3, the 3 holds 1
5. (2,5,1) → (7,0,1) - put 5 into 8
6. (7,0,1) → (7,1,0) - then 3 into 5
7. (7,1,0) → (4,1,3) - fill 3 from 8
8. (4,1,3) → (4,4,0) - put it into 5

State Space Chart

Recreating the state space chart

The Python program egypt creates dot language output, suitable for graphviz processing into an image. You could recreate the chart above like this (from the Linux command line, of course):

./egypt > egypt.dot
dot -Tpng -o egypt.png egypt.dot