BlueHash Algorithm Documentation - 中文文档

Overview

The BlueHash algorithm is a custom cryptographic hash function designed to generate secure hash values with varying bit lengths (128, 256, and 512 bits). It utilizes multiple rounds of transformations, including state updates, permutation functions, and constant generation, all of which contribute to the uniqueness and security of the final hash output.

This documentation provides an explanation of the algorithm's core components, including the state size, round counts, constant generation, and state update transformations. Mathematical formulas are provided to describe each step in the process.

Use Example

//You need to add the hex library to cargo.toml to print out the final hash, hex = “0.4.3”
extern crate hex;

fn main() {
    let key: u64 = 0x1234567890abcdef;
    let data = b"Hello, world! This is a test message for BlueHash.";

    // Create a 128-bit BlueHash instance
    let hash_algorithm_128 = BlueHash::BlueHash::new(BlueHash::DigestSize::Bit128, key);
    let mut hasher_128 = hash_algorithm_128;
    hasher_128.update(data);
    let hash_result_128 = hasher_128.finalize();

    // Create a 256-bit BlueHash instance
    let hash_algorithm_256 = BlueHash::BlueHash::new(BlueHash::DigestSize::Bit256, key);
    let mut hasher_256 = hash_algorithm_256;
    hasher_256.update(data);
    let hash_result_256 = hasher_256.finalize();

    // Create a 512-bit BlueHash instance
    let hash_algorithm_512 = BlueHash::BlueHash::new(BlueHash::DigestSize::Bit512, key);
    let mut hasher_512 = hash_algorithm_512;
    hasher_512.update(data);
    let hash_result_512 = hasher_512.finalize();

    println!("The full 128-bit hash result is: 0x{}", hex::encode(hash_result_128));
    println!("The full 256-bit hash result is: 0x{}", hex::encode(hash_result_256));
    println!("The full 512-bit hash result is: 0x{}", hex::encode(hash_result_512));
}

You will get output for example code

The full 128-bit hash result is: 0x6a2f8f3572697616894a8a0d02eb42f3
The full 256-bit hash result is: 0xb668bc23ecf63a45071829d992140992985c7323b43387cc617f0c7537764025
The full 512-bit hash result is: 0x73c2ef6642efeda5bb00b3385b6a644e9791ff29a06c559b4723a76f168312010b8cc657b130b720d77cccad2c2137b2ba5c5efdd817d5d1743b6420d065a29d

Key Components

1. State Size and Digest Length

The BlueHash algorithm uses a fixed state size and different digest lengths based on the desired output size.

• State Size: 25 64-bit words, i.e., ( STATE_SIZE = 25 ).
• Digest Length: Based on the digest size, which can be 128, 256, or 512 bits.

The number of rounds and the output length for each digest size are as follows:

$$ R(d) = \begin{cases} 56, & \text{if } d = 128 \text{ bits} \\ 64, & \text{if } d = 256 \text{ bits} \\ 80, & \text{if } d = 512 \text{ bits} \end{cases} $$

$$ L(d) = \begin{cases} 16, & \text{if } d = 128 \text{ bits} \\ 32, & \text{if } d = 256 \text{ bits} \\ 64, & \text{if } d = 512 \text{ bits} \end{cases} $$

2. Constants Generation

The generate_constants function generates a unique constant for each round of the hash transformation. The constant is based on several factors, including the round number, input data, and predefined constants.

The constant is generated using the following formula:

$$ \text{constant} = \left( p \ll (r \mod 64) \right) \times \left( r + \text{round factor} \right) \ll 32 + \left( r + \text{round factor} \right) \gg 16 + \text{extra prime} \ll (r \mod 32) + \text{noise} \ll 8 + \text{hash length} $$

Where:

• ( p ) is a fixed prime constant.
• ( r ) is the round number.
• round_factor is a function of the round number.
• extra_prime is a large constant prime.
• noise is generated from the input data and round number.
• hash_length is the length of the final digest.

This ensures that each round has a unique constant, enhancing the security and randomness of the hash process.

3. State Update and Permutation

The update and permute functions implement the core transformation logic of the algorithm. Each round involves updating the state using the current round constants and applying various bitwise operations to achieve diffusion and confusion.

The update formula for the state state[i] at round r is as follows:

$$ \text{state}[i] = \left( \text{state}[i] \ll 29 \right) + \text{constant} + \text{local\ vars}[2] \oplus \left( \text{local\ vars}[0] \land \text{local\ vars}[1] \right) \oplus \left( \text{local\ vars}[3] \gg 17 \right) \oplus \left( \text{constant} \ll 23 \right) $$

Where:

• state[i] is the i^{th} element of the state array.
• local vars are variables derived from neighboring state values.
• << and >> represent bitwise left and right shifts, respectively.
• ⊕ represents the bitwise XOR operation.
• & represents the bitwise AND operation.

This transformation ensures that each round of the hash function introduces non-linear mixing, which helps in achieving both diffusion (small input changes lead to large output changes) and confusion (output is not easily related to the input).

4. Finalizing the Hash

The final hash is produced by extracting bits from the internal state after all rounds of transformations are complete. The final digest is generated by taking chunks of 64 bits from the state and converting them to bytes.

The formula for generating the final digest is:

$$ \text{digest}[j] = \text{state}\left[\frac{j}{8} \mod \text{STATE\ SIZE}\right] $$

Where:

• digest[j] is the j^{th} byte of the final hash.
• state[j / 8 mod STATE_SIZE] represents the value taken from the state array.

The resulting bytes are concatenated to form the final hash value, which is the output of the finalize function.

5. Correctness and Security

The security of the BlueHash algorithm is based on the following principles:

• Uniqueness: Each round uses a unique constant that depends on the round number, input data, and a series of primes. This ensures that no two rounds produce the same transformation.
• Collision Resistance: The non-linear transformations and mixing of state variables at each round make it computationally difficult to find two distinct inputs that produce the same hash output.
• Diffusion and Confusion: The bitwise operations (XOR, AND, shifts) used in the state update function ensure that small changes in the input lead to significantly different hash values, which is the essence of a good cryptographic hash function.

By adhering to these principles, BlueHash is designed to be a robust cryptographic hash function, resistant to attacks such as collision finding and pre-image attacks.

Compare to SHA-3 (NIST)

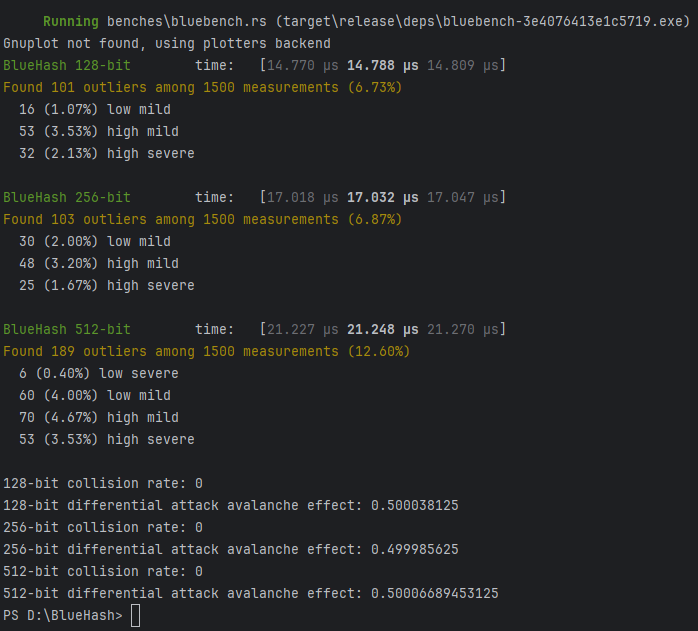
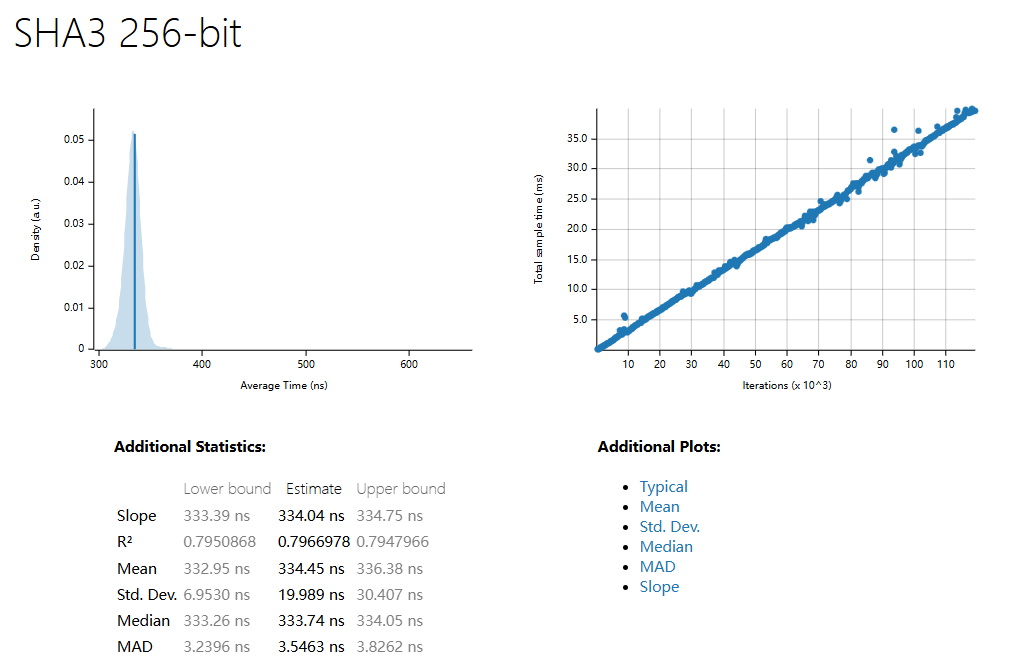
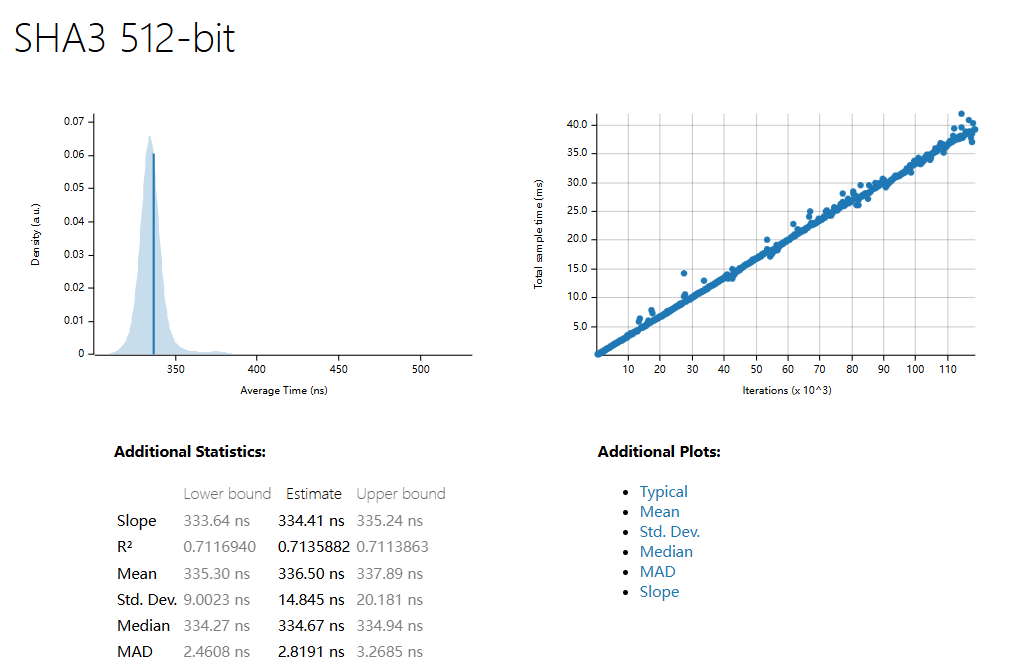
1500 Sample	SHA3 256	SHA3 512	BlueHash 128	BlueHash 256	BlueHash 512
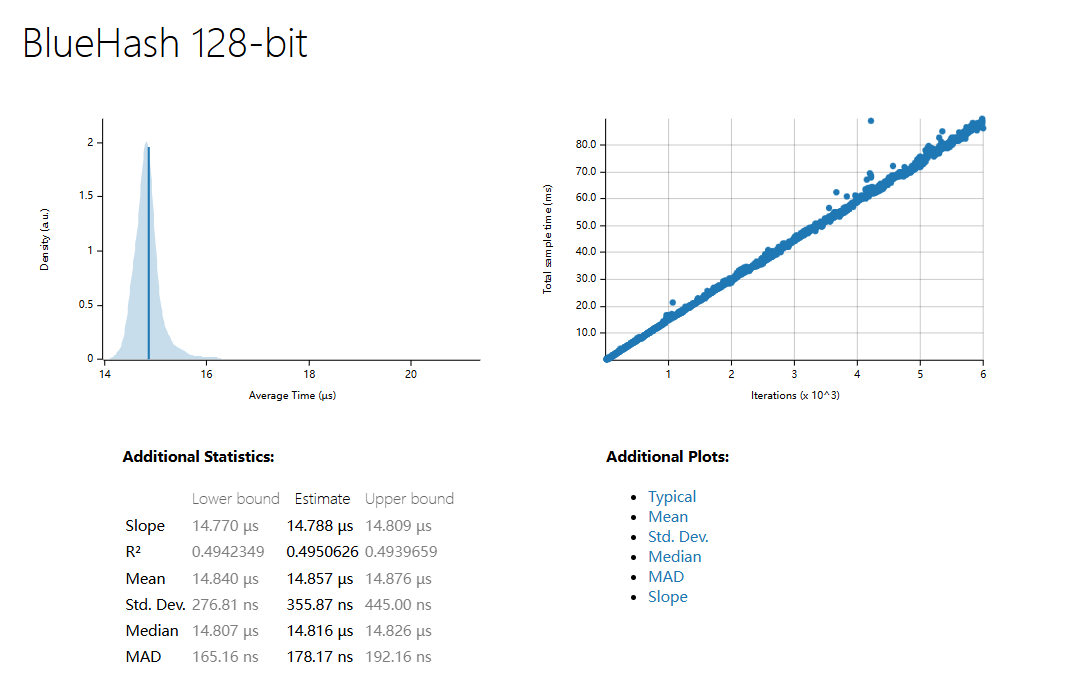
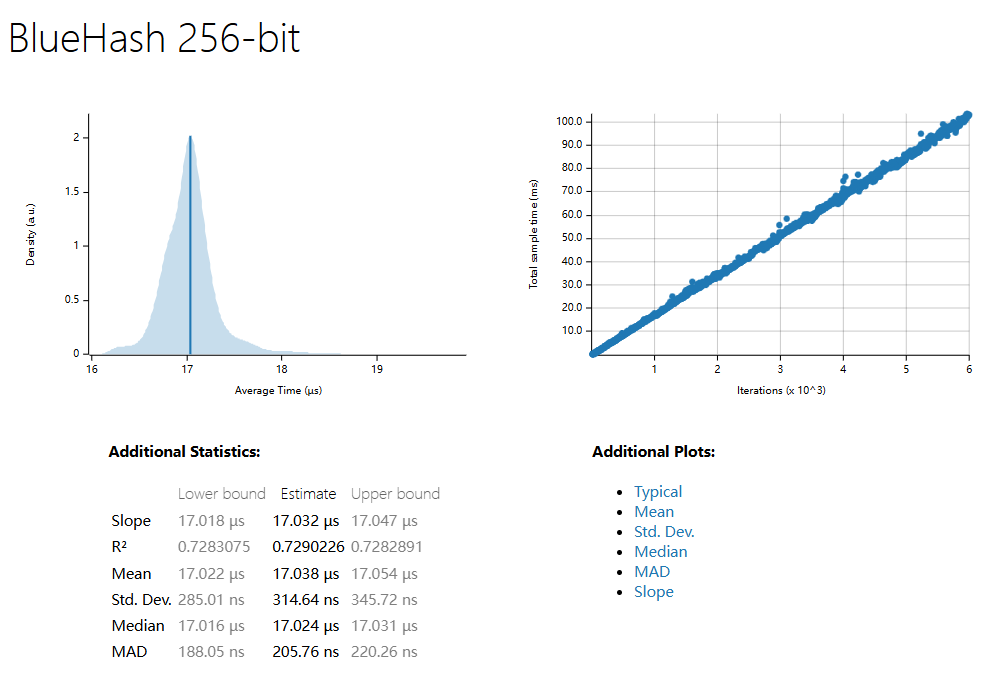
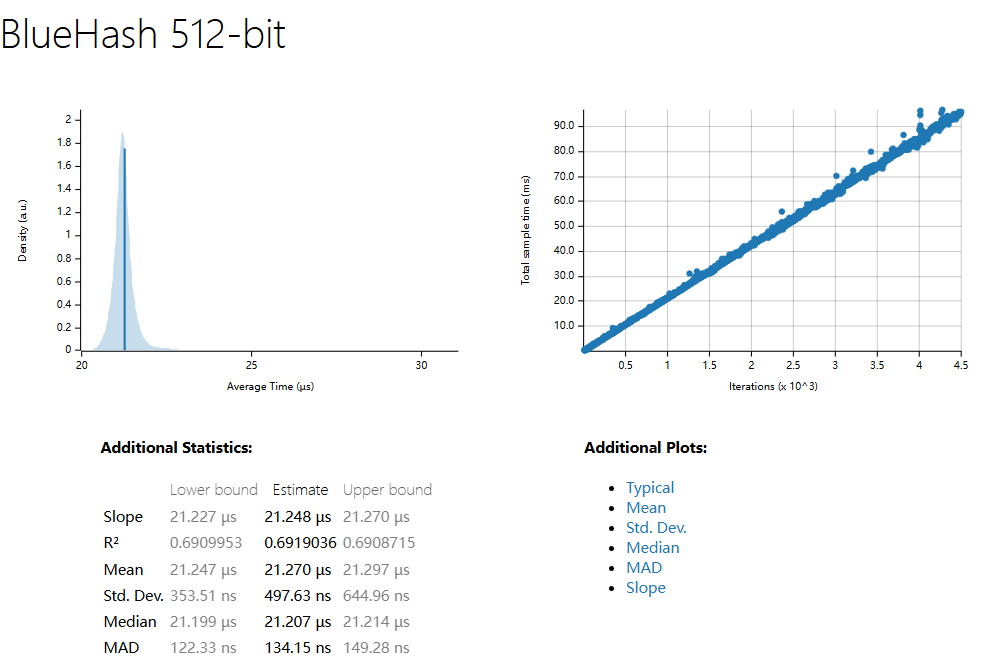
Slope	334.04 ns	334.41 ns	14.788 µs	17.032 µs	21.248 µs
R^2	0.7966978	0.7135882	0.4950626	0.7290226	0.6919036
Mean	334.45 ns	336.50 ns	14.857 µs	17.038 µs	21.270 µs
std. Dev	19.989 ns	14.845 ns	355.87 ns	314.64 ns	497.63 ns
Median	333.74 ns	334.67 ns	14.816 µs	17.024 µs	21.207 µs
MAD	3.5463 ns	2.8191 ns	178.17 ns	205.76 ns	134.15 ns

BenchMark for BlueHash and SHA3

BlueHash-128 (1500 Samples)

BlueHash-256 (1500 Samples)

BlueHash-512 (1500 Samples)

BlueHash Differential Attack (1500 Samples and 10 Million Trial Attack)

SHA3-256 (1500 Samples)

SHA3-512 (1500 Samples)

What is BlueHash Algorithm Pros and Cons?

The BlueHash algorithm has the following advantages over SHA3-256:

1. Resistance to Quantum Attacks: Provides greater resistance to quantum attacks through the mechanism of LWE noise and constant generation.

2. Higher Randomness and Complexity: Utilizes dynamic generation of constants, increasing the unpredictability of the hash algorithm. This adds complexity and makes the algorithm more resistant to differential attacks.

3. Stronger State Update and Replacement: Offers improved resistance to both conventional and quantum attacks through more diverse bit operations and hybrid operations.

4. Enhanced Noise Generation Mechanism: The addition of LWE noise not only increases security but also enhances defense, particularly against quantum computing.

5. Flexibility: Enables flexible adjustment of rounds and other parameters according to different hash lengths, optimizing performance while ensuring security.

Potential Limitations of BlueHash

1. Higher Performance Overhead: Multiple rounds of complex operations and noise generation increase the computational overhead and may impact efficiency in big data processing.

2. Higher Memory Consumption: More local variables and state storage requirements may lead to performance bottlenecks in low-memory environments.

3. Lack of Standardization and Auditing: Compared to SHA3-256, BlueHash lacks extensive security auditing and community validation, which may affect its trustworthiness in certain applications.

---

The BlueHash algorithm is a custom cryptographic hash function that leverages multiple rounds of complex transformations to generate secure hashes of varying lengths. It utilizes a fixed state size, round-based transformations, and constant generation to ensure the uniqueness and security of the final output.

---

Donations

USDT : Arbitrum One Network: 0x4051d34Af2025A33aFD5EacCA7A90046f7a64Bed	USDC: Arbitrum One Network: 0x4051d34Af2025A33aFD5EacCA7A90046f7a64Bed	Dash: Dash Network: XuJwtHWdsYzfLawymR3B3nDdS2W8dHnxyR