torch-optimizer

torch-optimizer -- collection of optimizers for PyTorch compatible with optim module.

Simple example

import torch_optimizer as optim

# model = ...
optimizer = optim.DiffGrad(model.parameters(), lr=0.001)
optimizer.step()

Installation

Installation process is simple, just:

$ pip install torch_optimizer

Documentation

https://pytorch-optimizer.rtfd.io

Supported Optimizers

A2GradExp	https://arxiv.org/abs/1810.00553
A2GradInc	https://arxiv.org/abs/1810.00553
A2GradUni	https://arxiv.org/abs/1810.00553
AccSGD	https://arxiv.org/abs/1803.05591
AdaBelief	https://arxiv.org/abs/2010.07468
AdaBound	https://arxiv.org/abs/1902.09843
AdaMod	https://arxiv.org/abs/1910.12249
Adafactor	https://arxiv.org/abs/1804.04235
Adahessian	https://arxiv.org/abs/2006.00719
AdamP	https://arxiv.org/abs/2006.08217
AggMo	https://arxiv.org/abs/1804.00325
Apollo	https://arxiv.org/abs/2009.13586
DiffGrad	https://arxiv.org/abs/1909.11015
Lamb	https://arxiv.org/abs/1904.00962
Lookahead	https://arxiv.org/abs/1907.08610
MADGRAD	https://arxiv.org/abs/2101.11075
NovoGrad	https://arxiv.org/abs/1905.11286
PID	https://www4.comp.polyu.edu.hk/~cslzhang/paper/CVPR18_PID.pdf
QHAdam	https://arxiv.org/abs/1810.06801
QHM	https://arxiv.org/abs/1810.06801
RAdam	https://arxiv.org/abs/1908.03265
Ranger	https://medium.com/@lessw/new-deep-learning-optimizer-ranger-synergistic-combination-of-radam-lookahead-for-the-best-of-2dc83f79a48d
RangerQH	https://arxiv.org/abs/1810.06801
RangerVA	https://arxiv.org/abs/1908.00700v2
SGDP	https://arxiv.org/abs/2006.08217
SGDW	https://arxiv.org/abs/1608.03983
SWATS	https://arxiv.org/abs/1712.07628
Shampoo	https://arxiv.org/abs/1802.09568
Yogi	https://papers.nips.cc/paper/8186-adaptive-methods-for-nonconvex-optimization

Visualizations

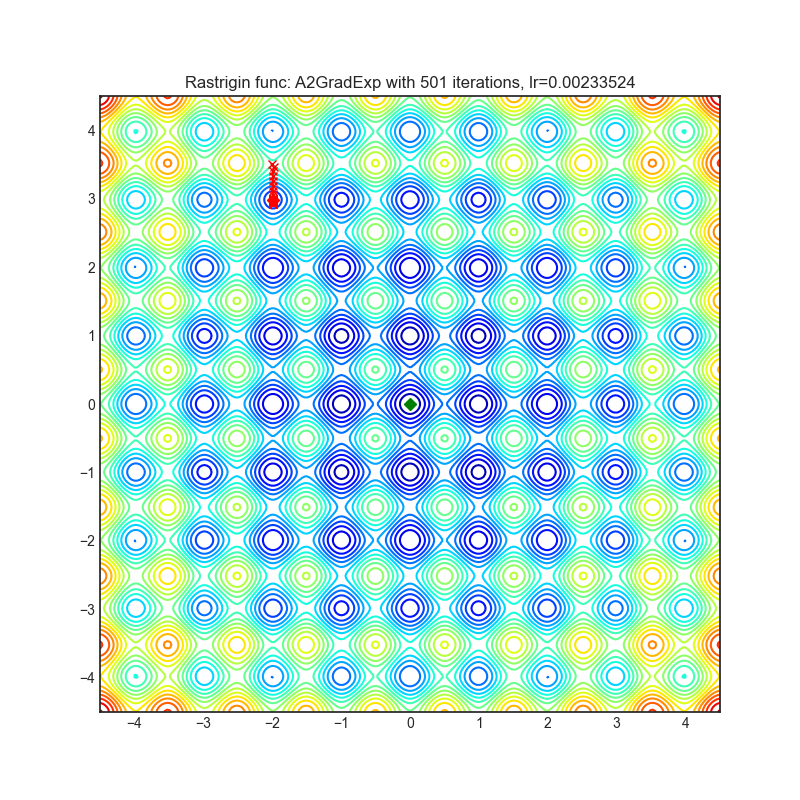
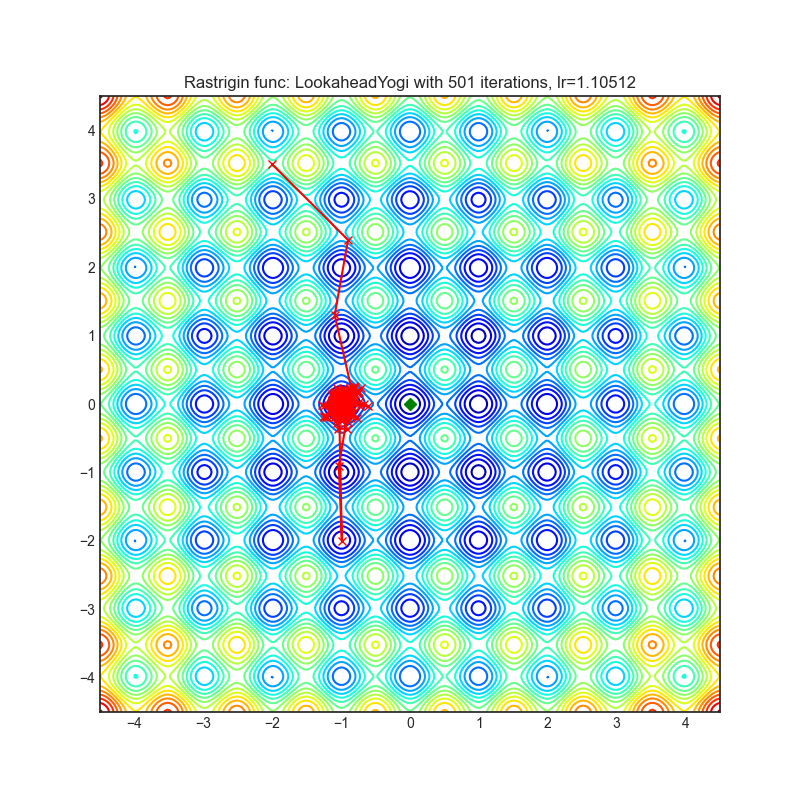
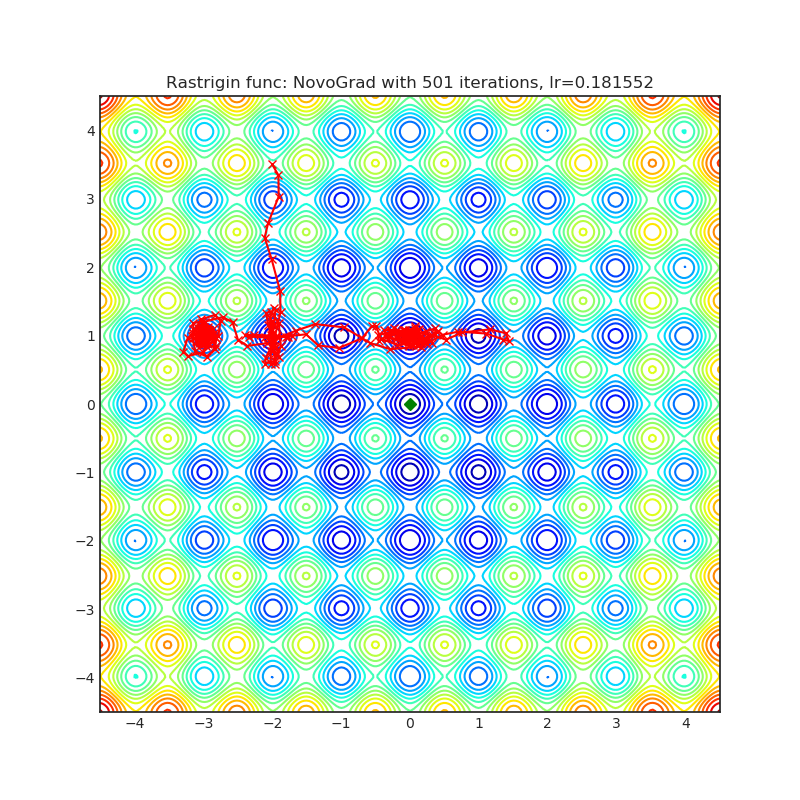
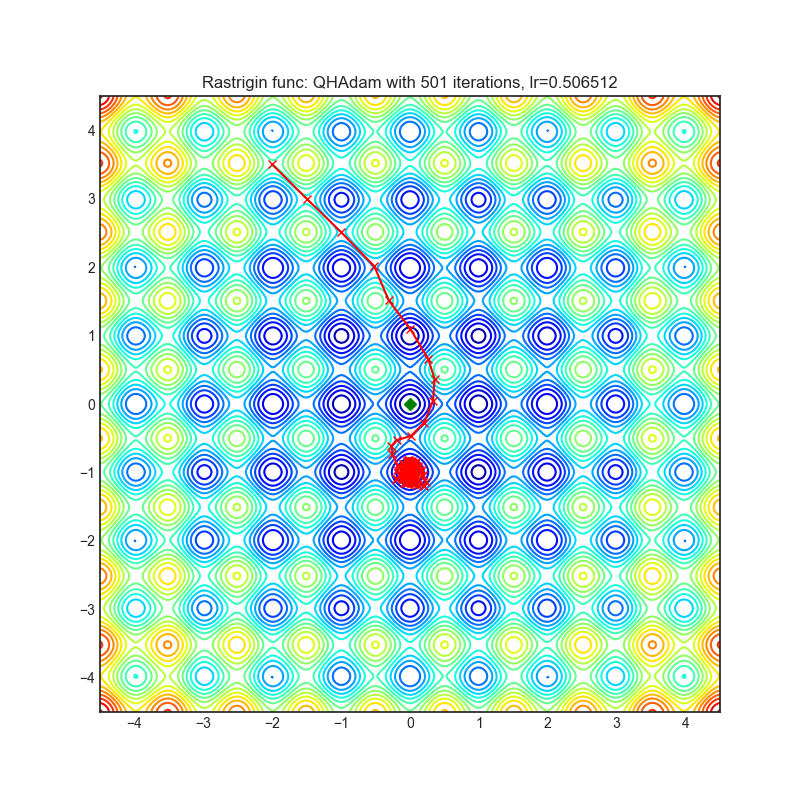
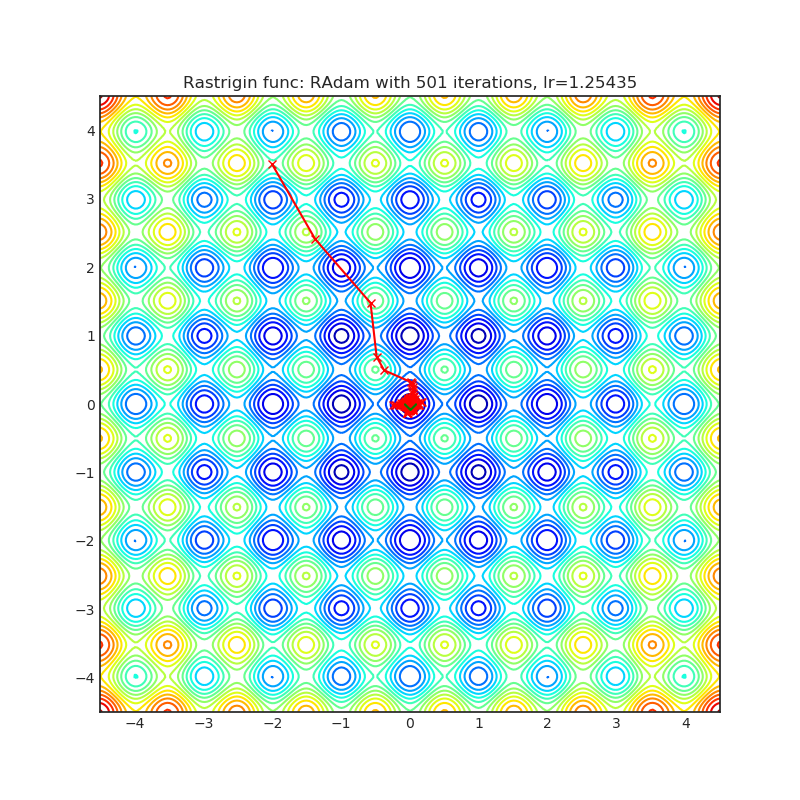
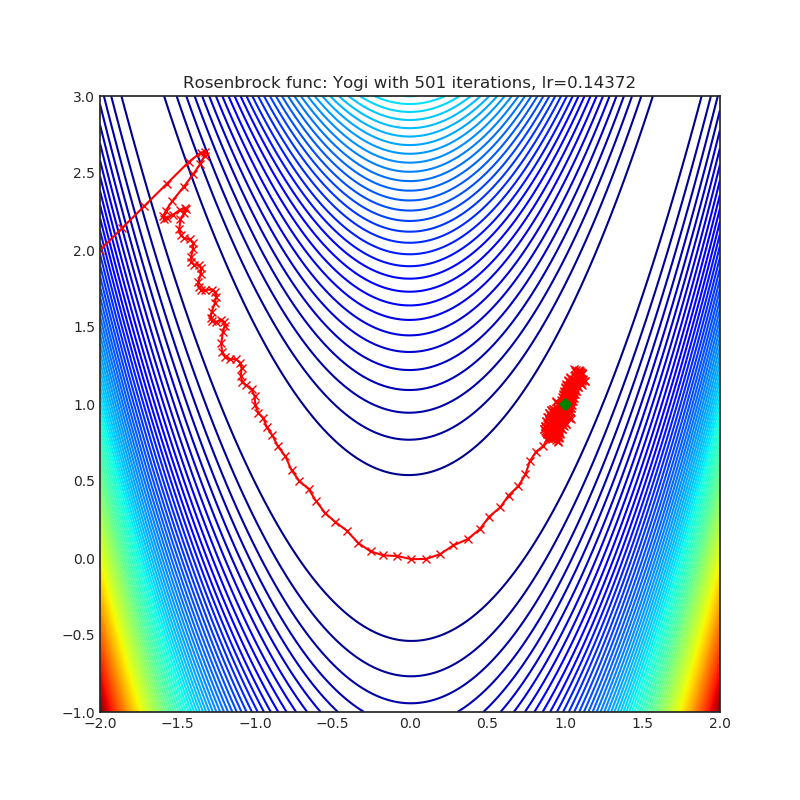
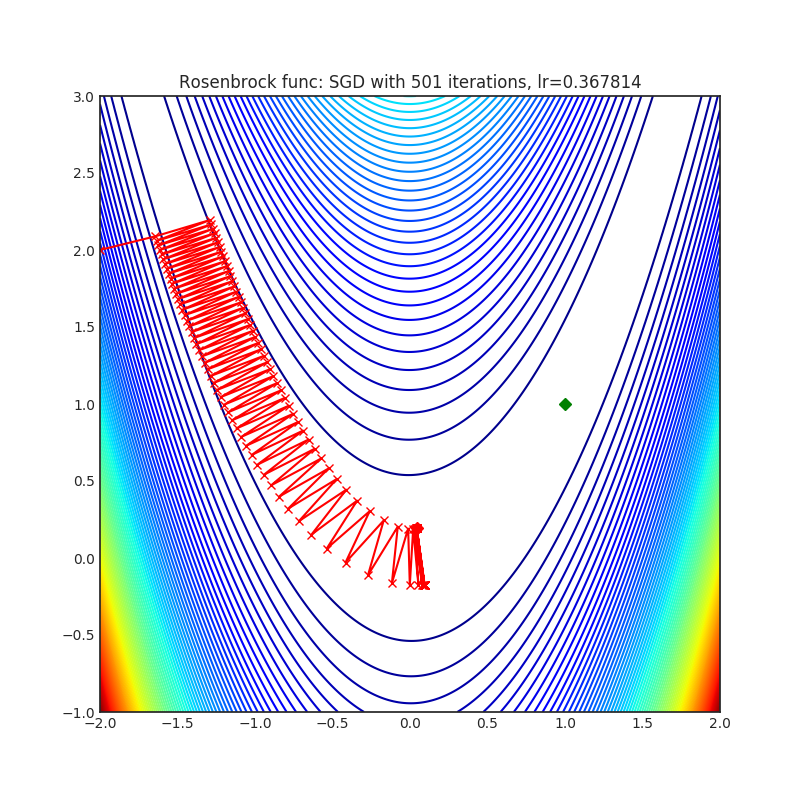
Visualizations help us to see how different algorithms deals with simple situations like: saddle points, local minima, valleys etc, and may provide interesting insights into inner workings of algorithm. Rosenbrock and Rastrigin benchmark functions was selected, because:

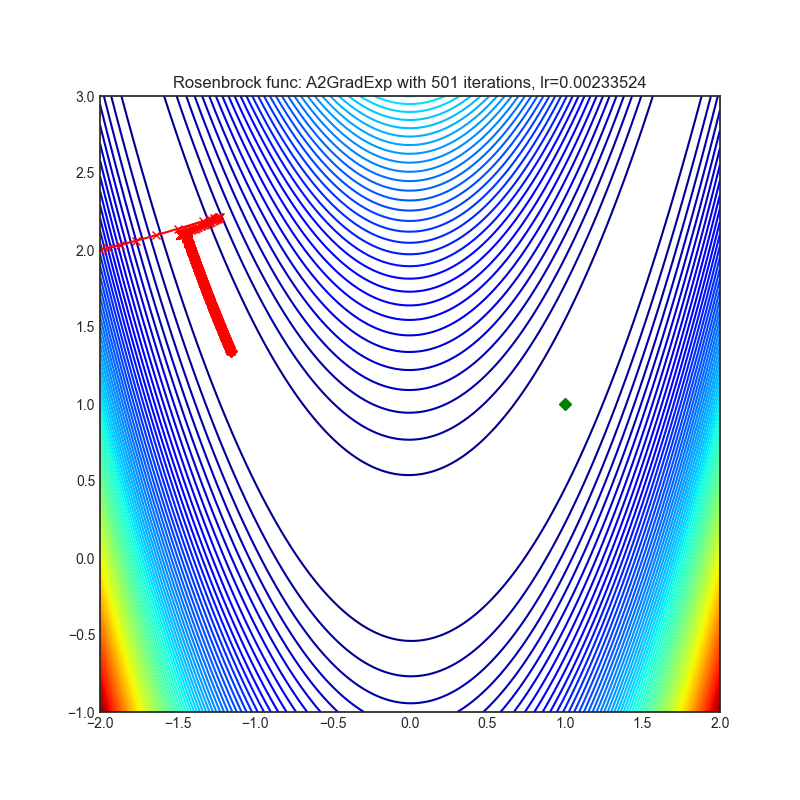
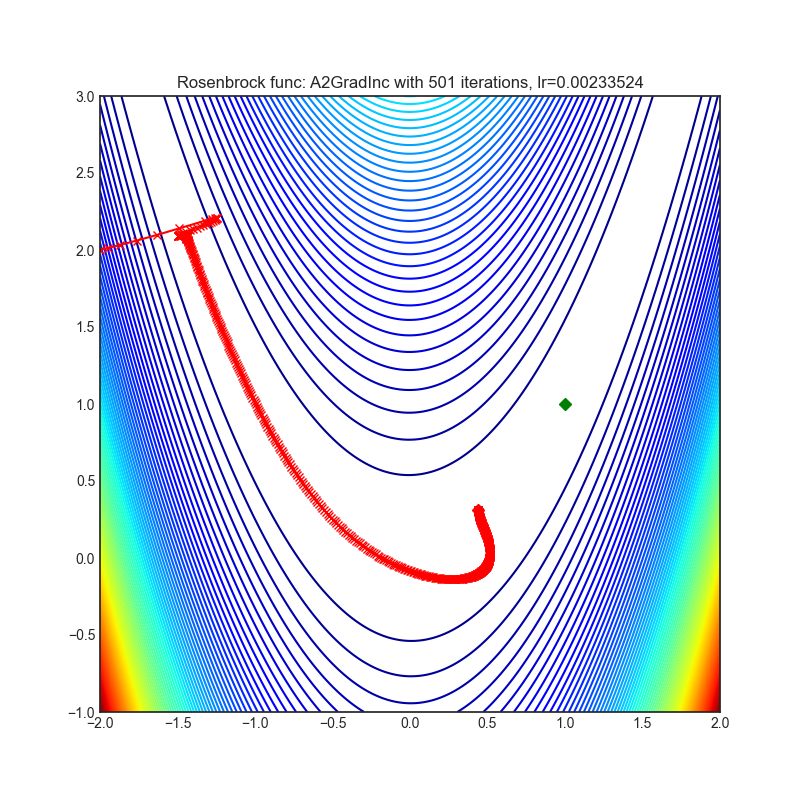
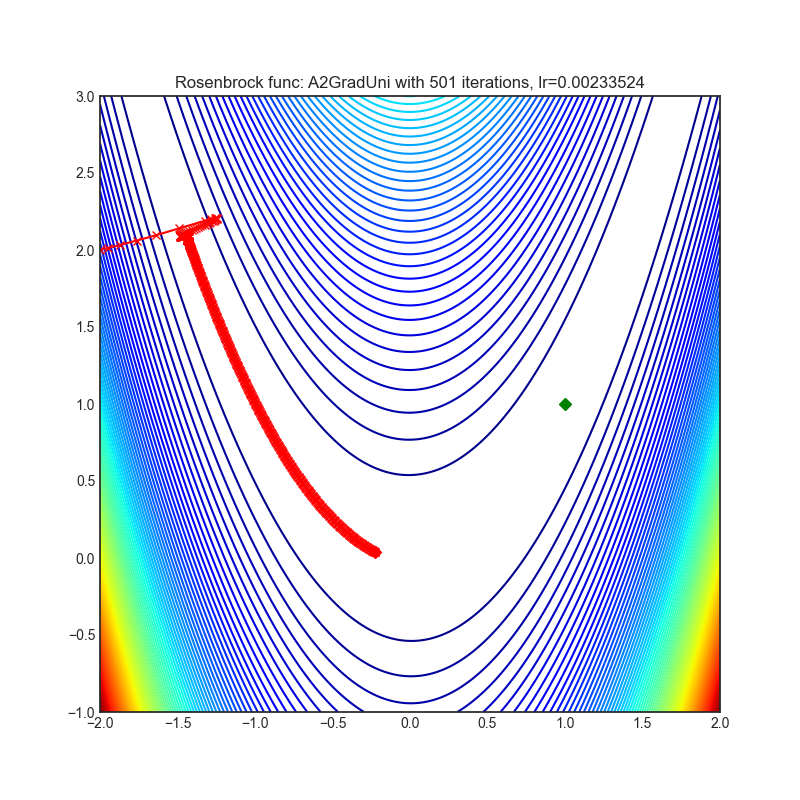
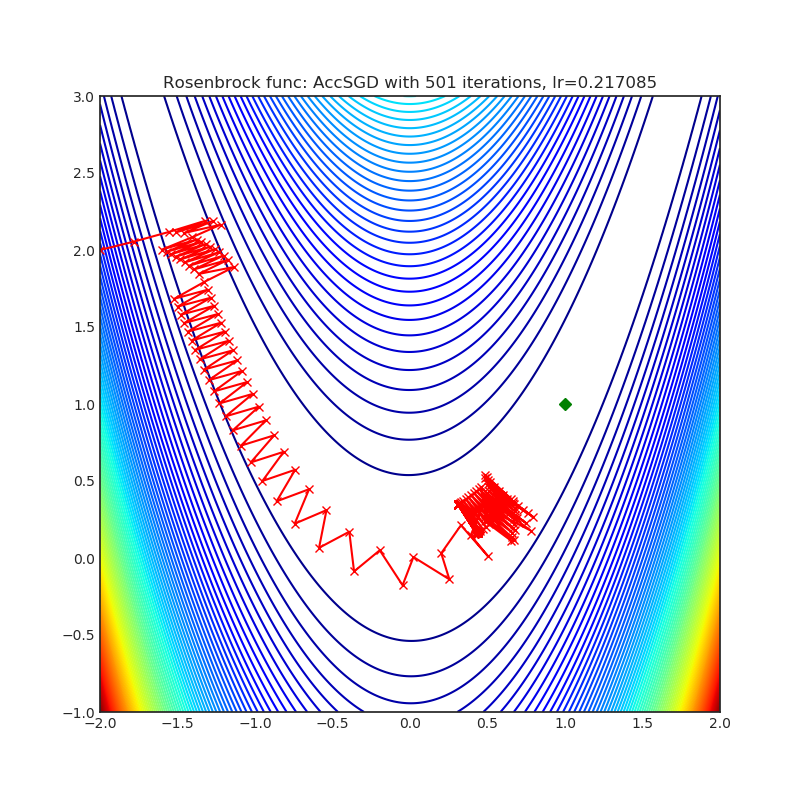
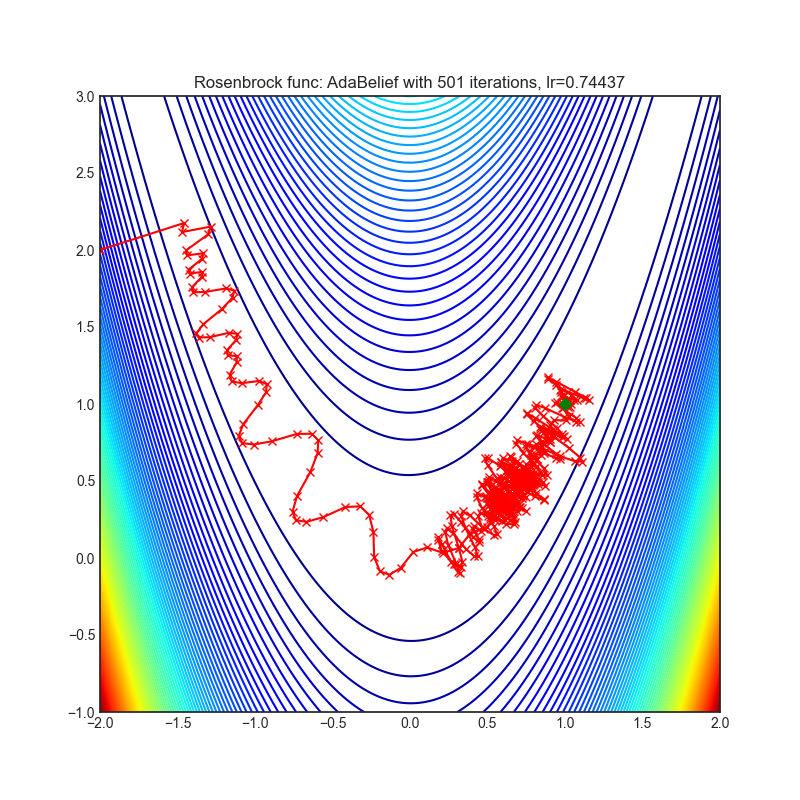
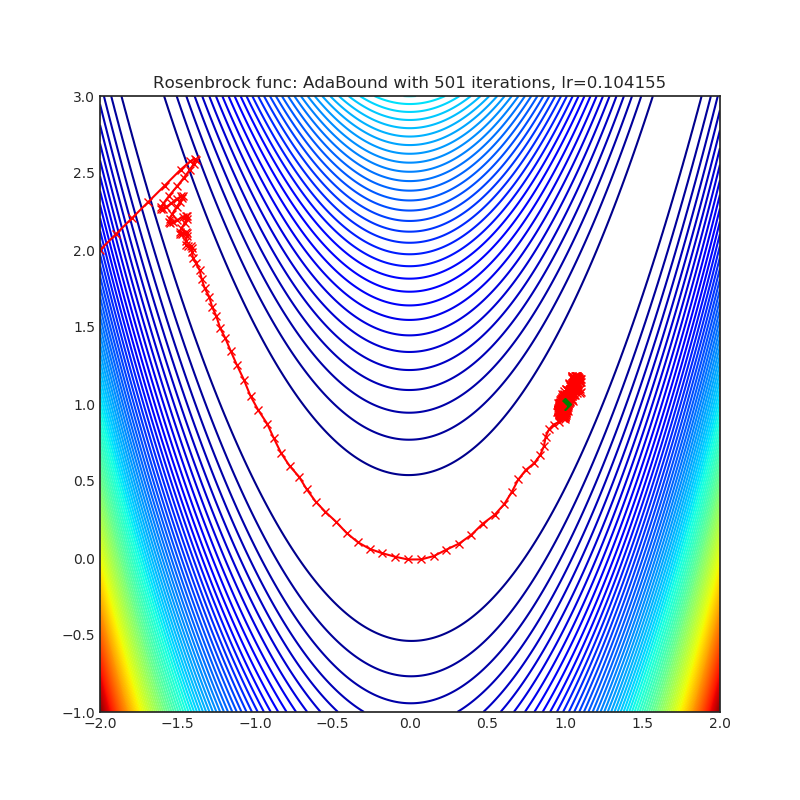
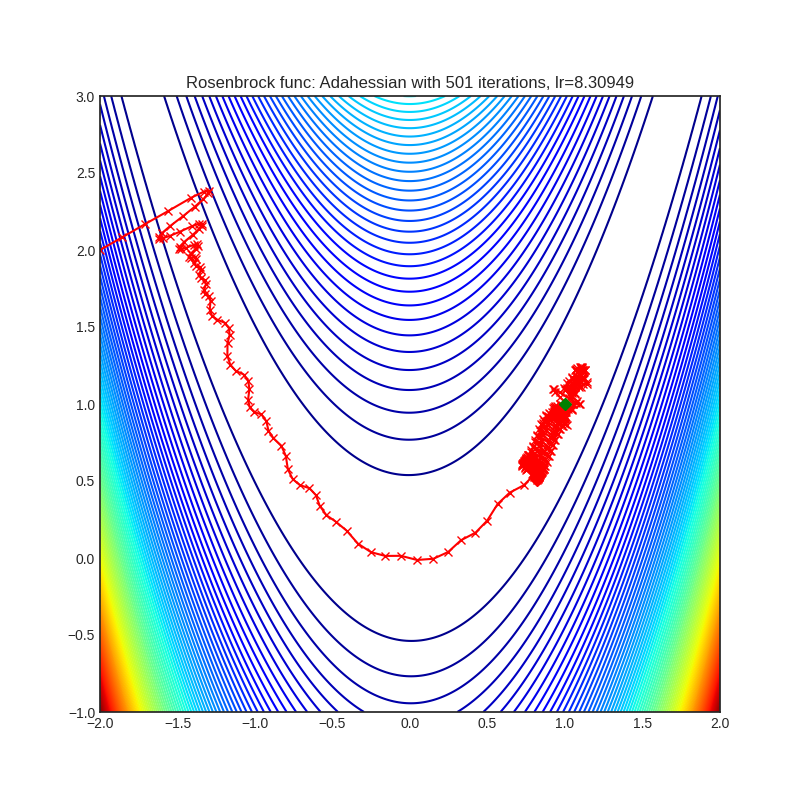
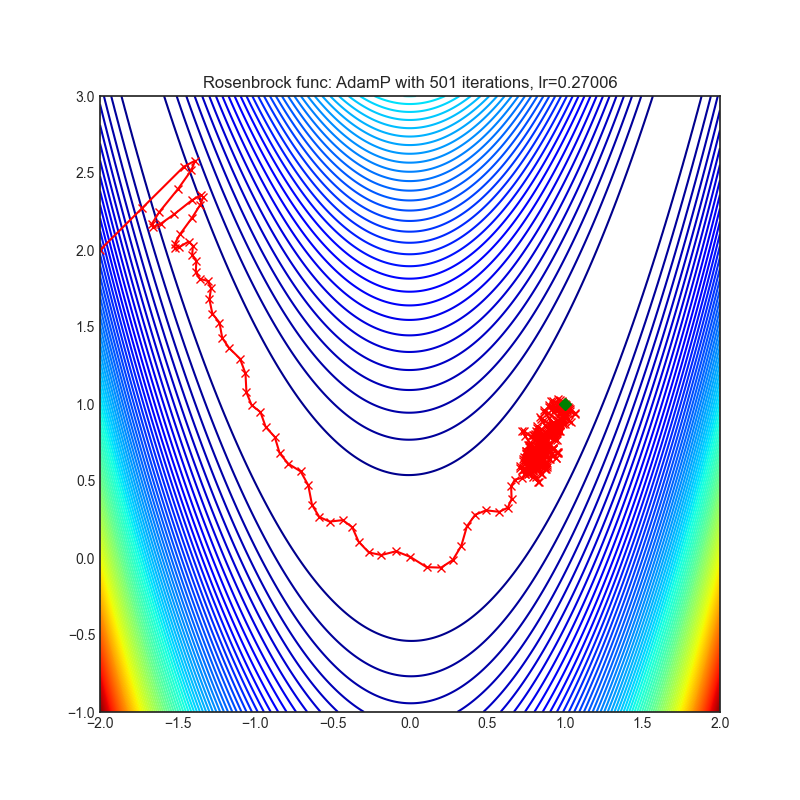
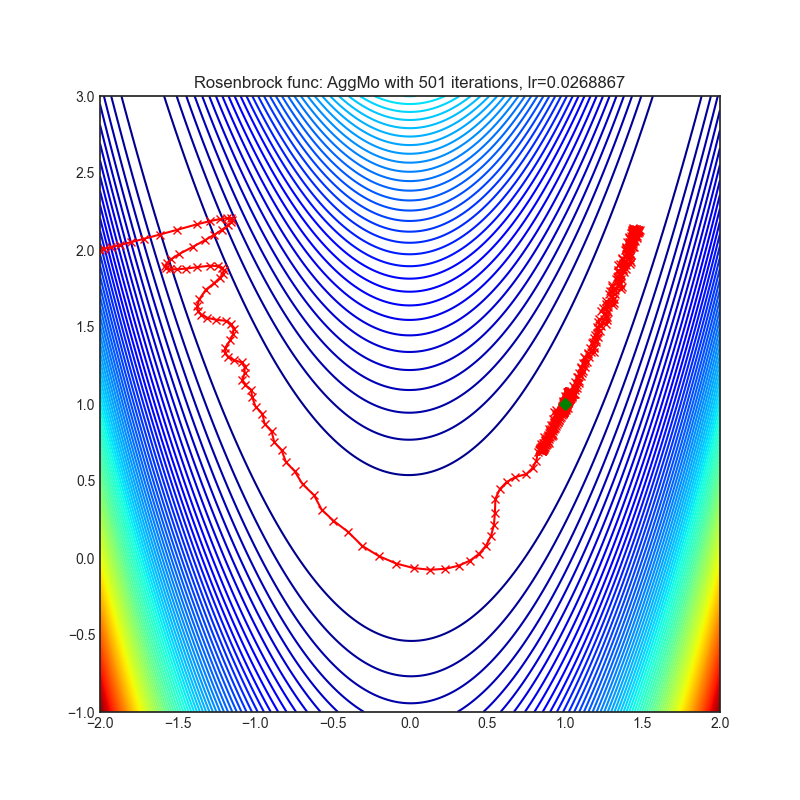
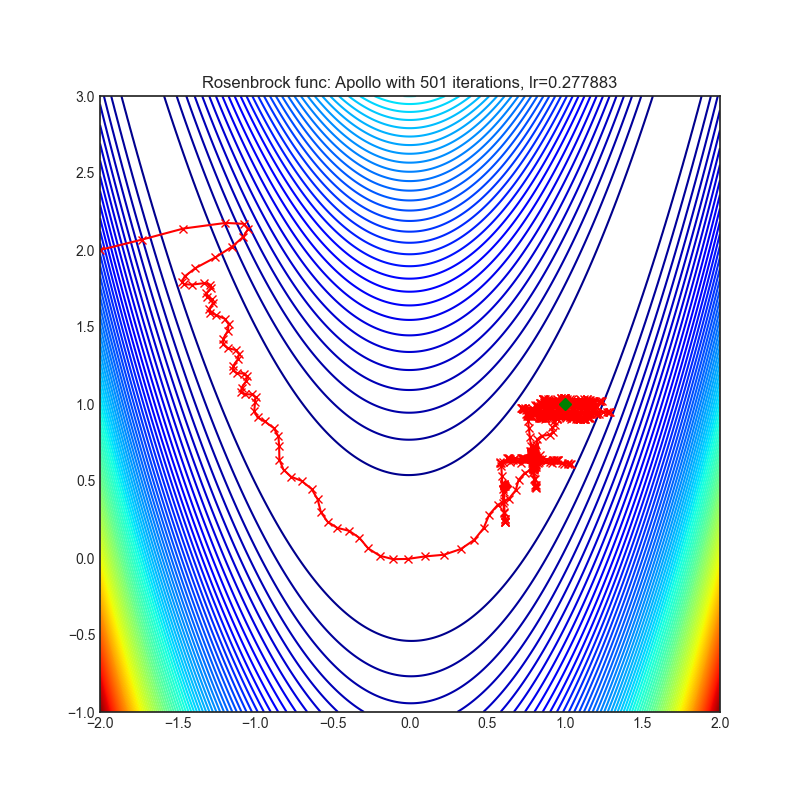
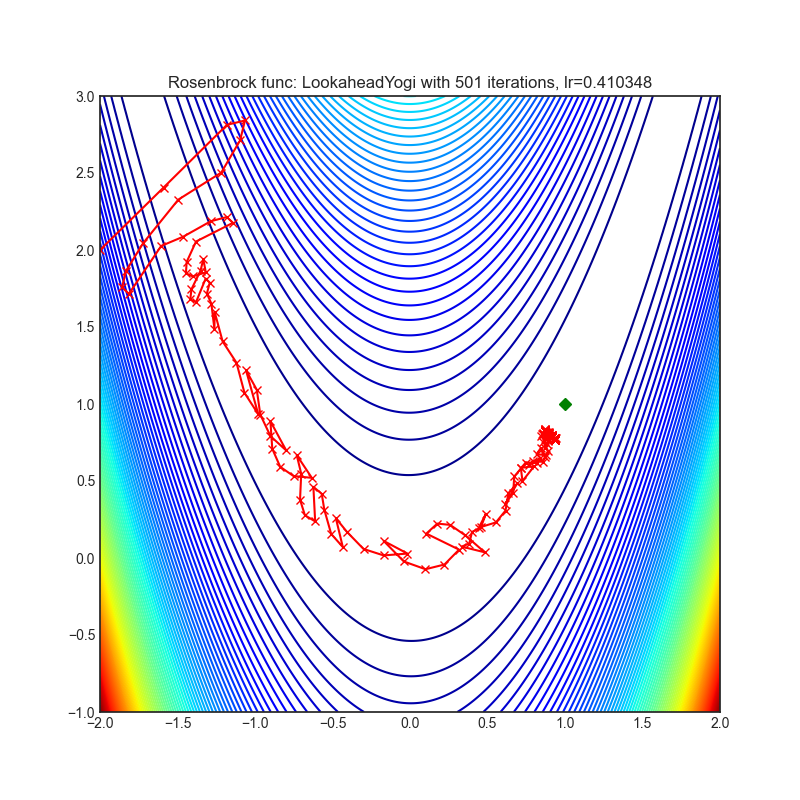
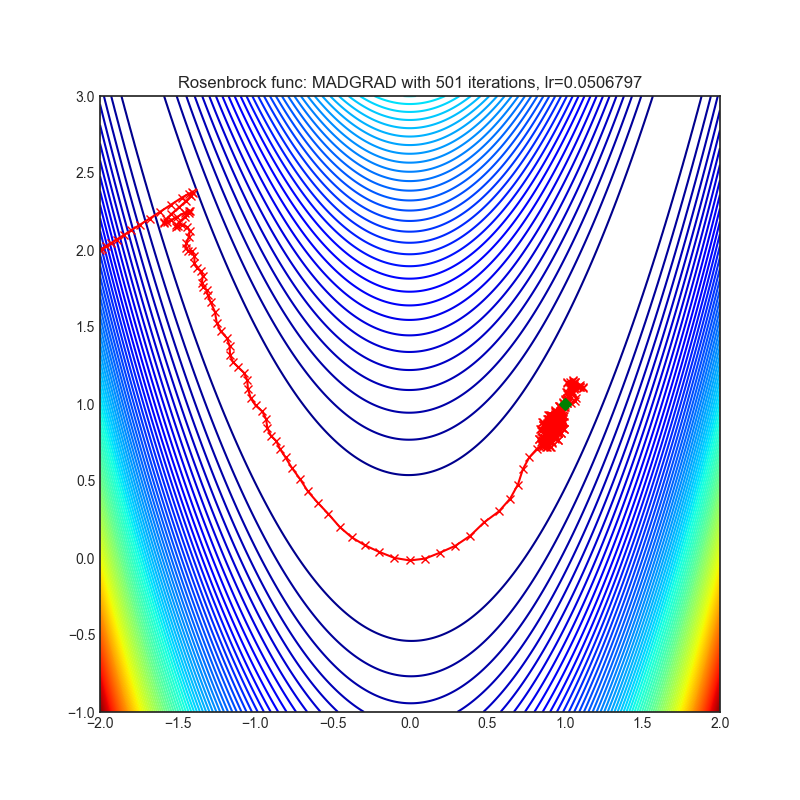
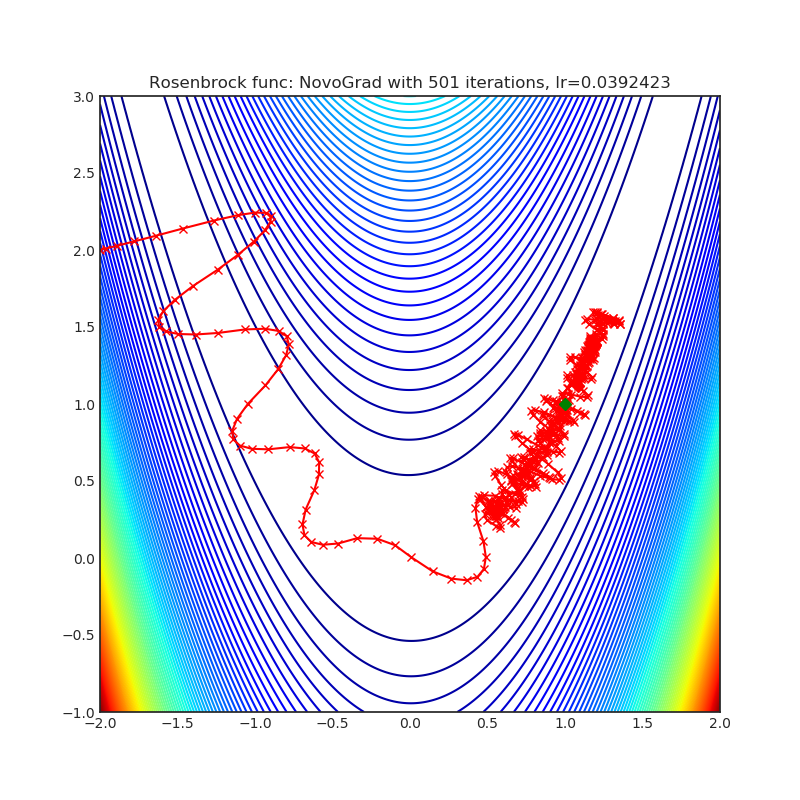
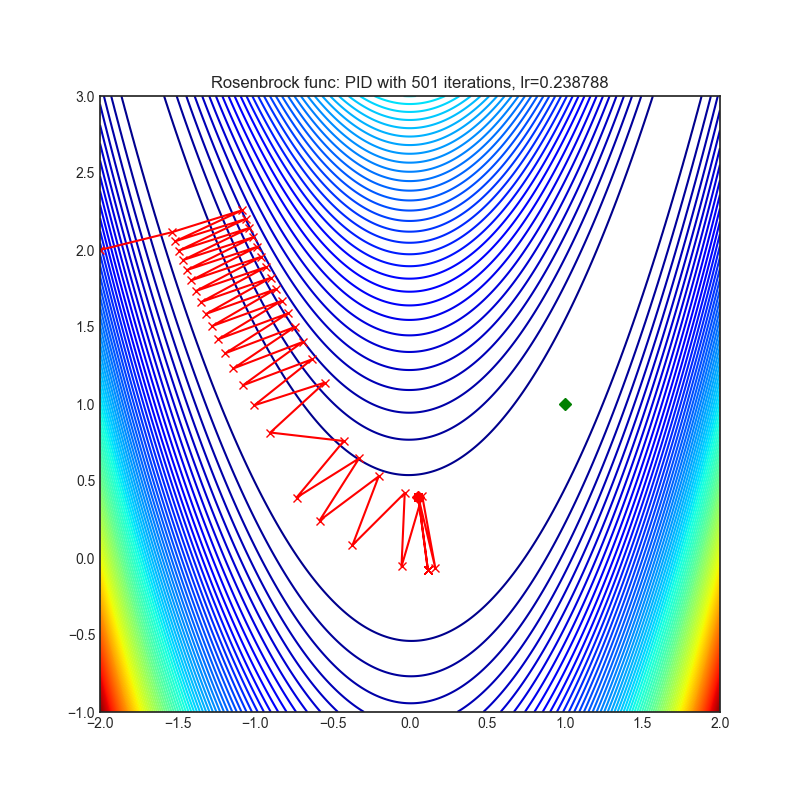
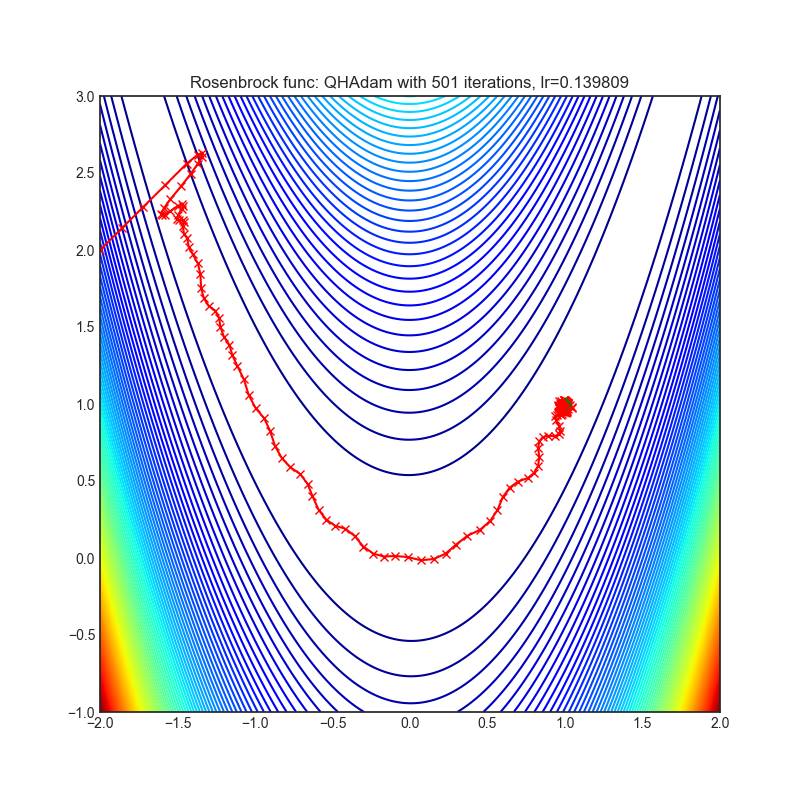
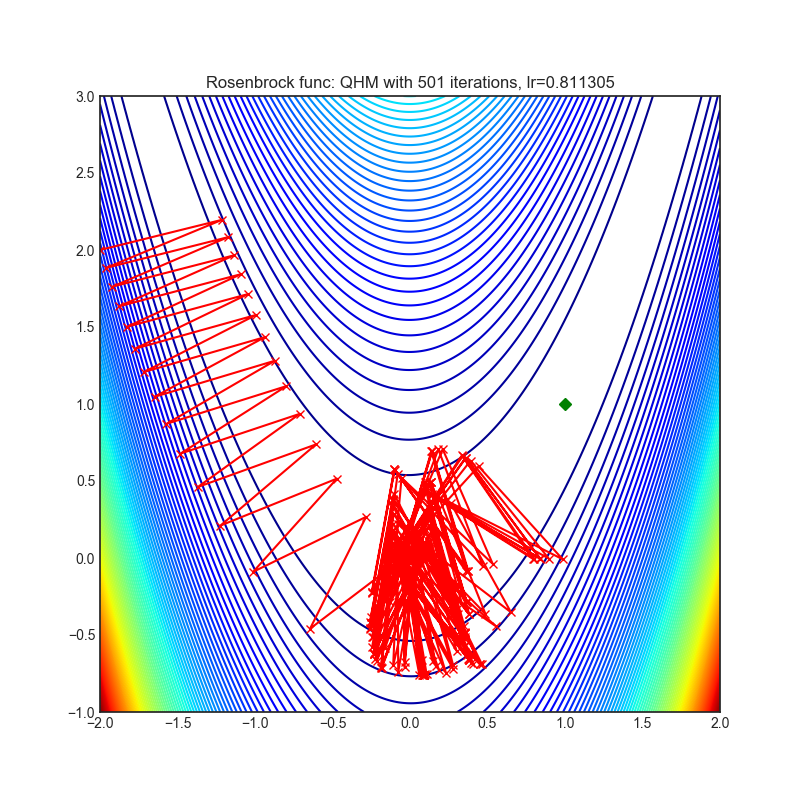
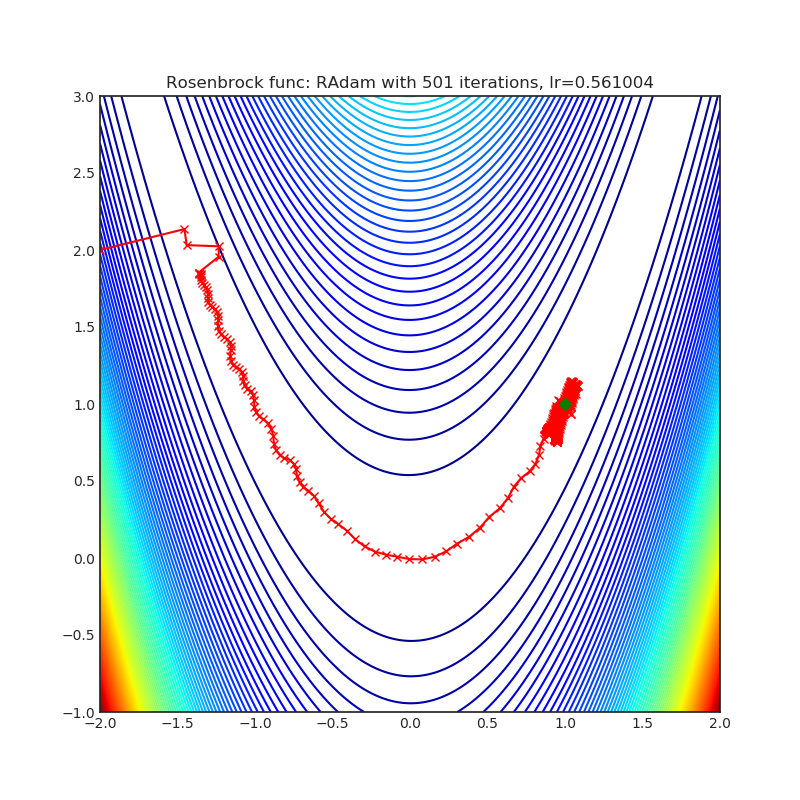
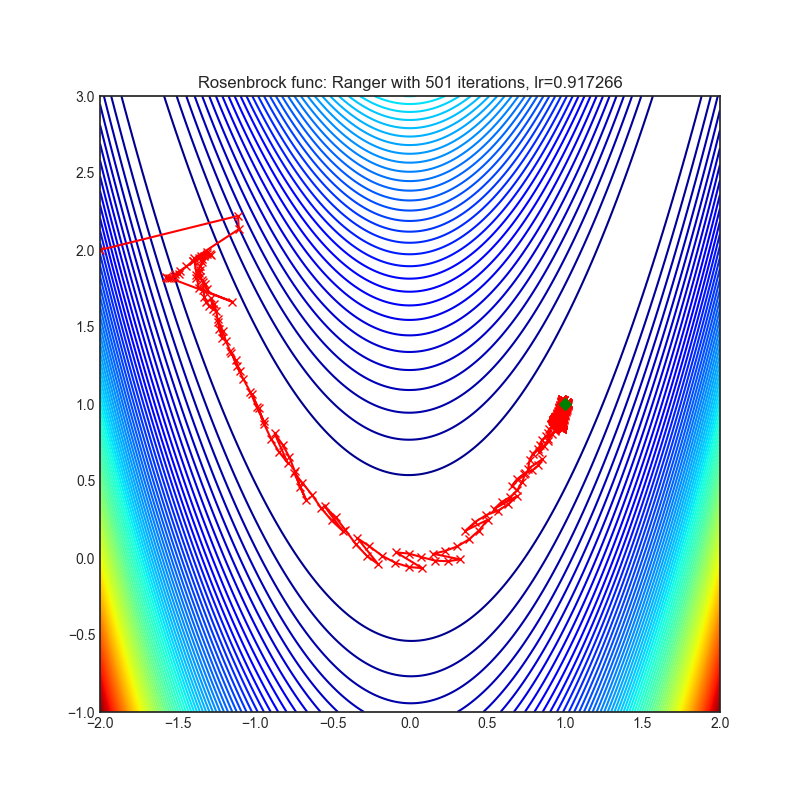
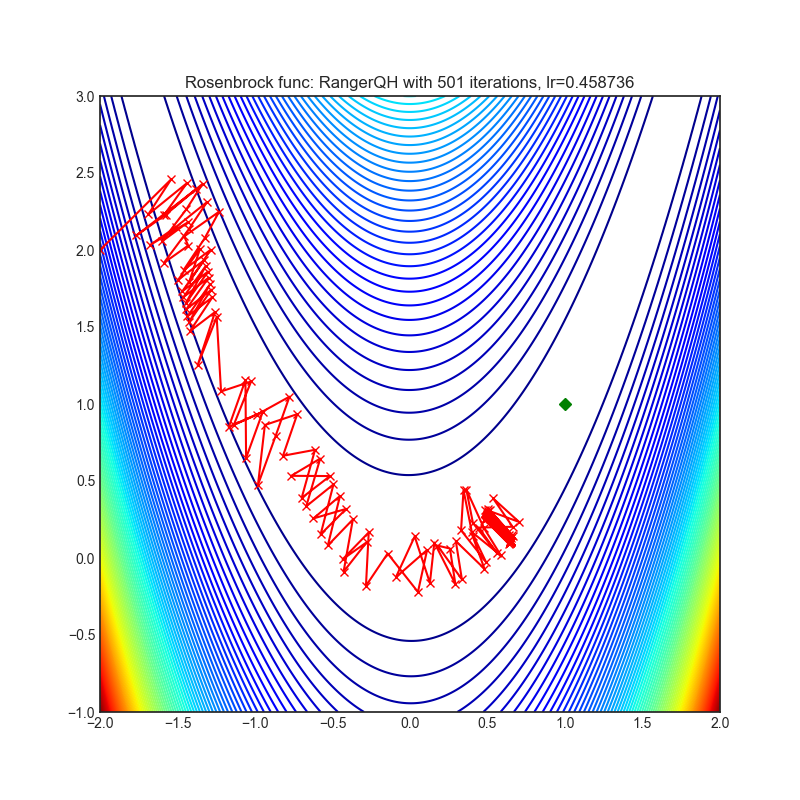
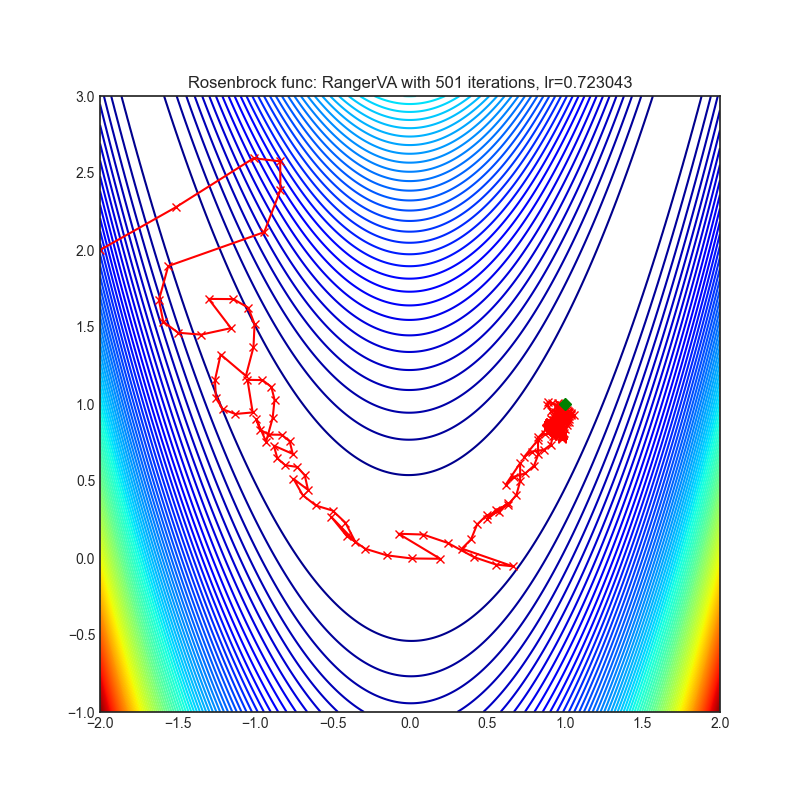
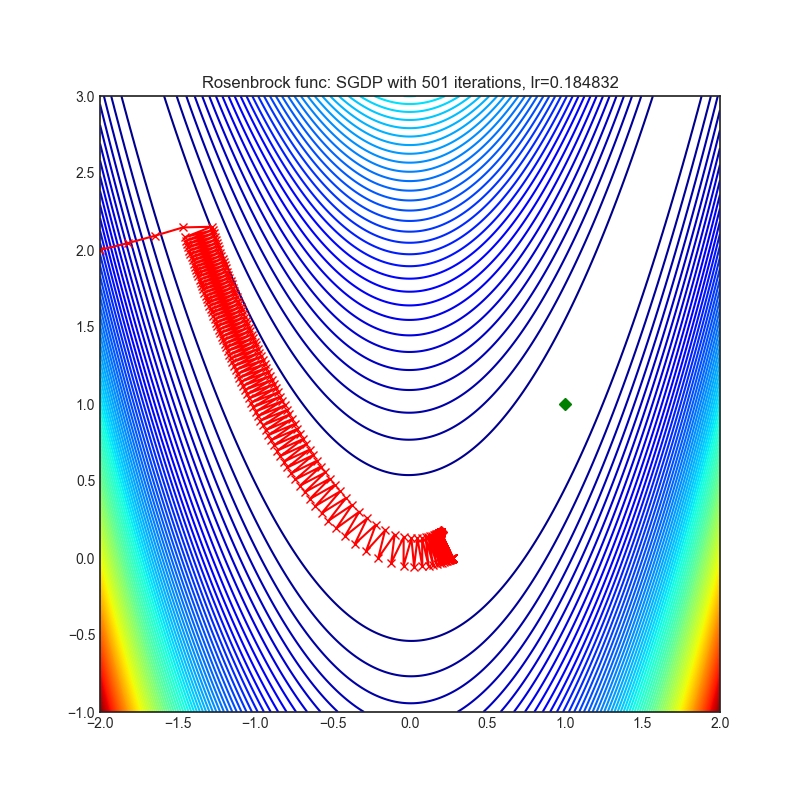
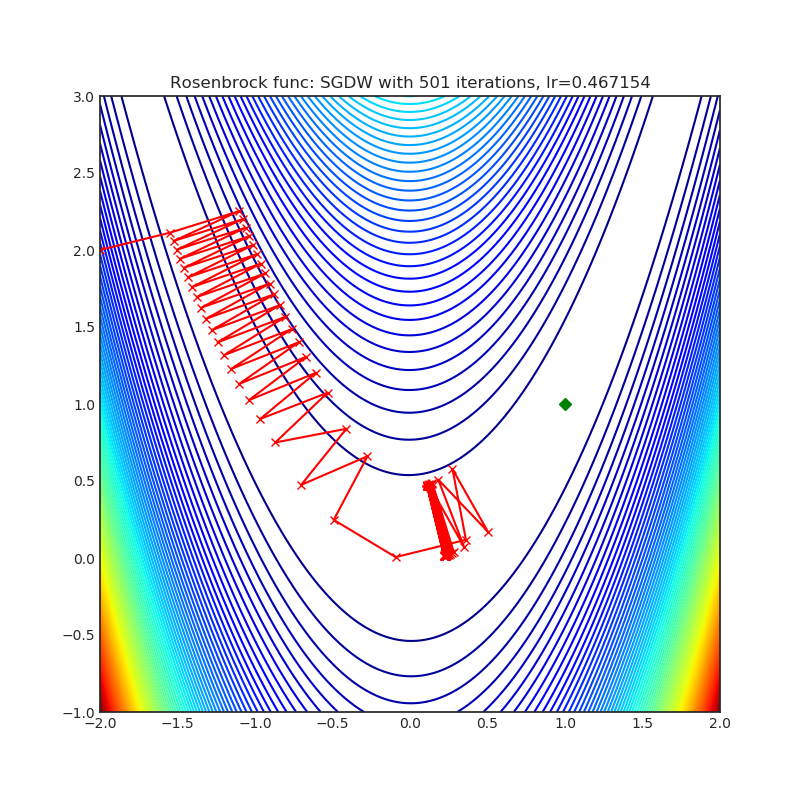
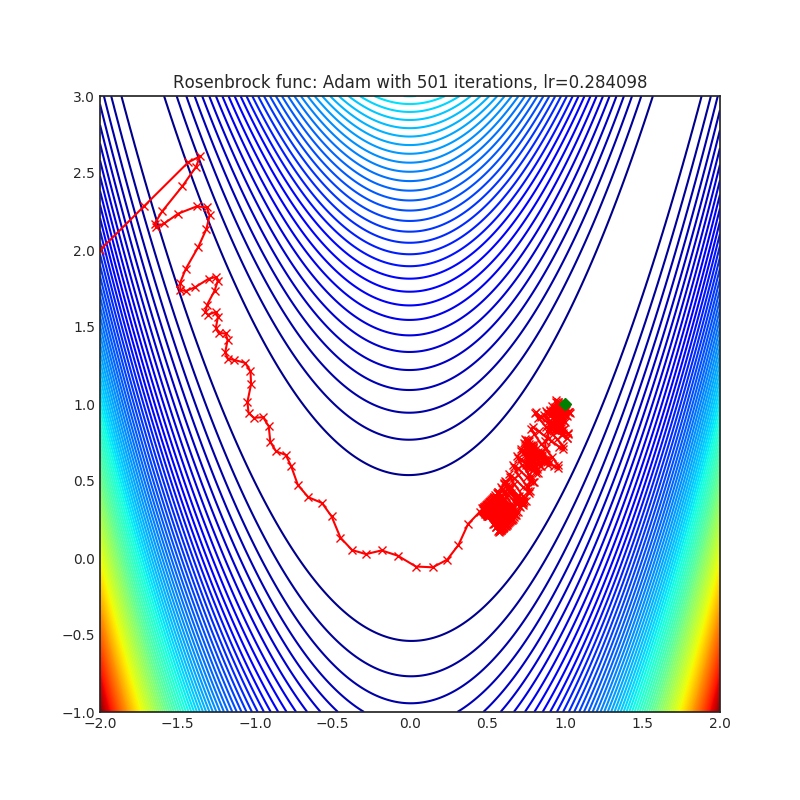
• Rosenbrock (also known as banana function), is non-convex function that has one global minima (1.0. 1.0). The global minimum is inside a long, narrow, parabolic shaped flat valley. To find the valley is trivial. To converge to the global minima, however, is difficult. Optimization algorithms might pay a lot of attention to one coordinate, and have problems to follow valley which is relatively flat.

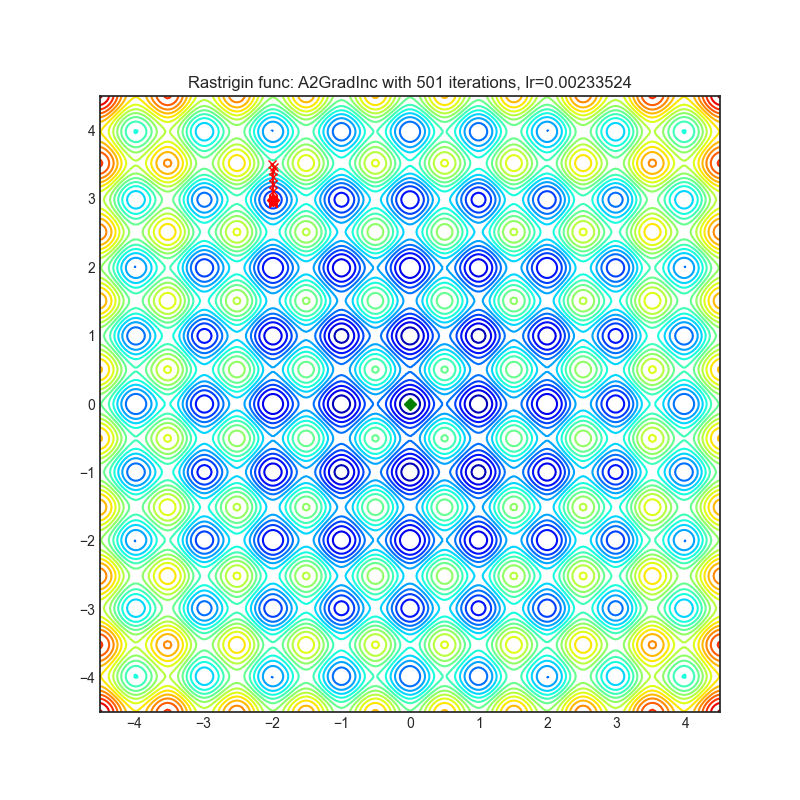
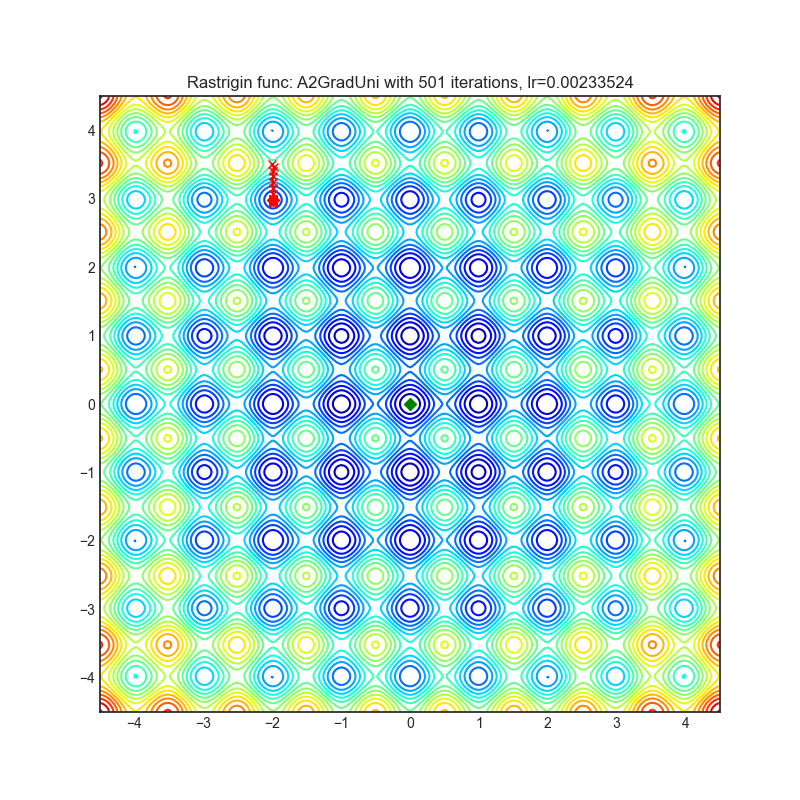
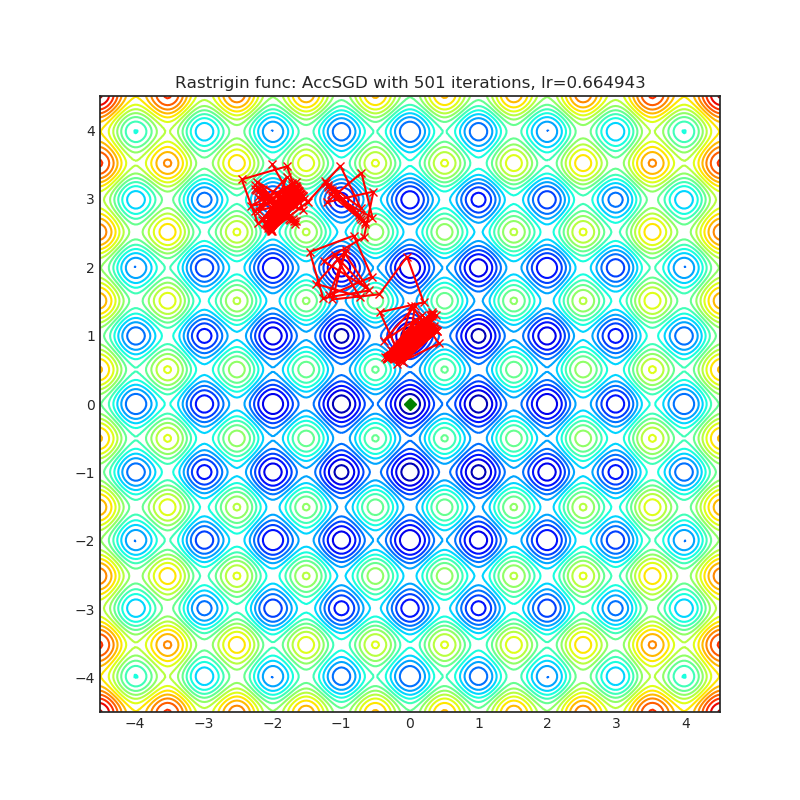
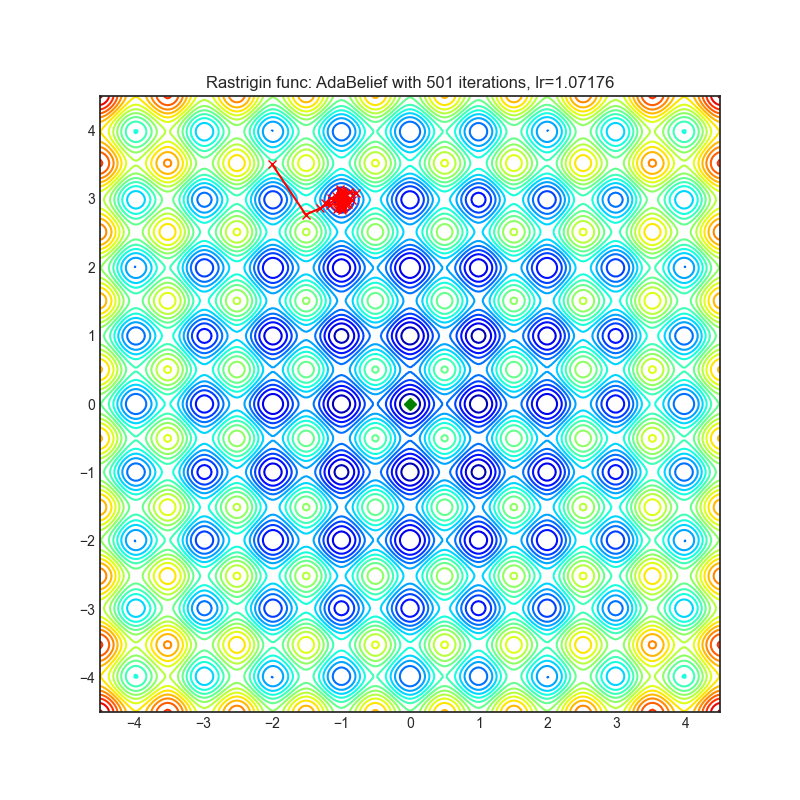
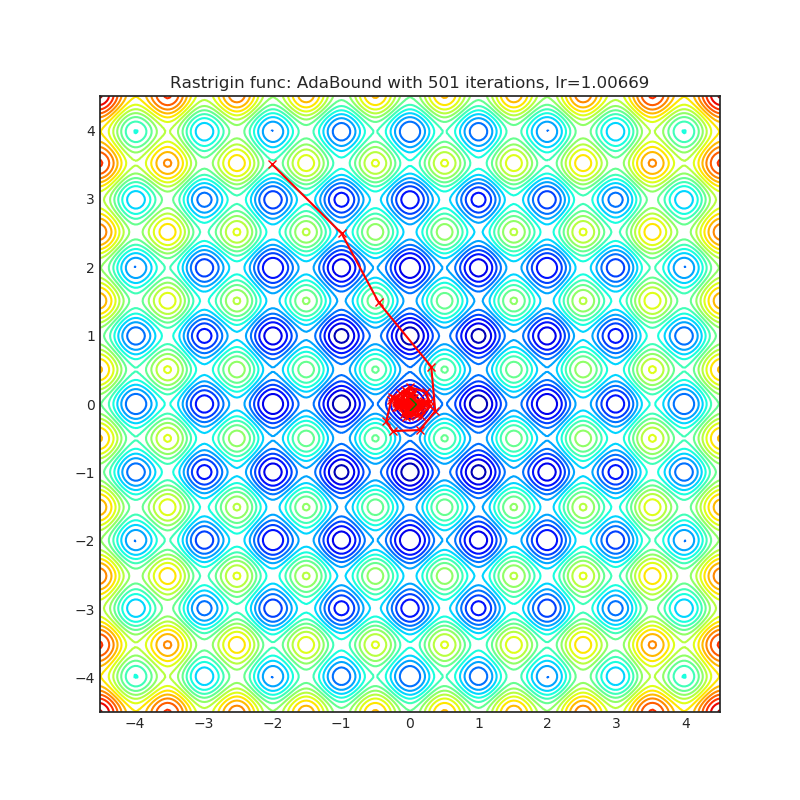
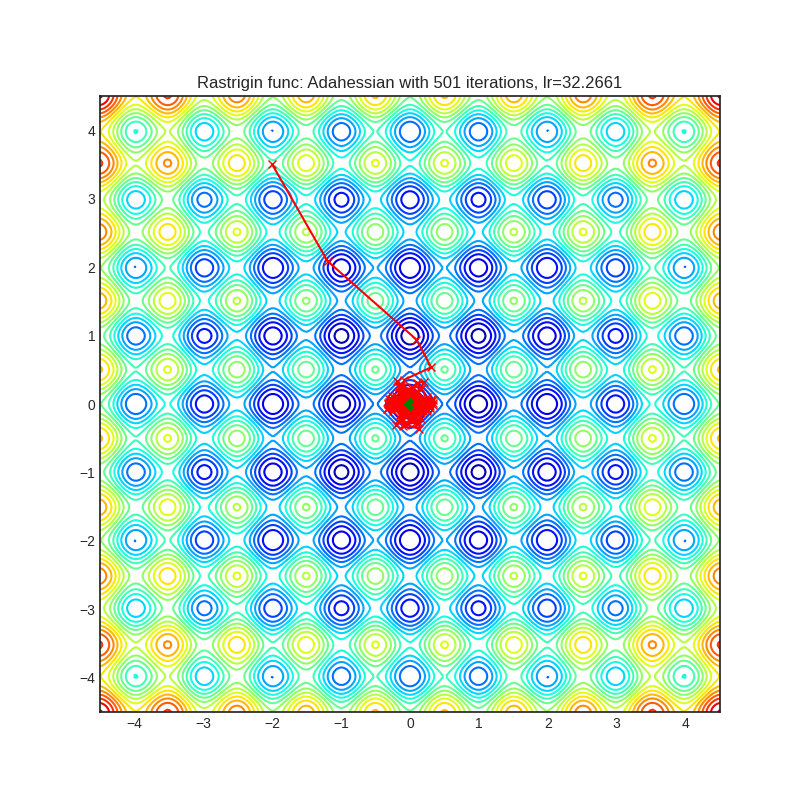
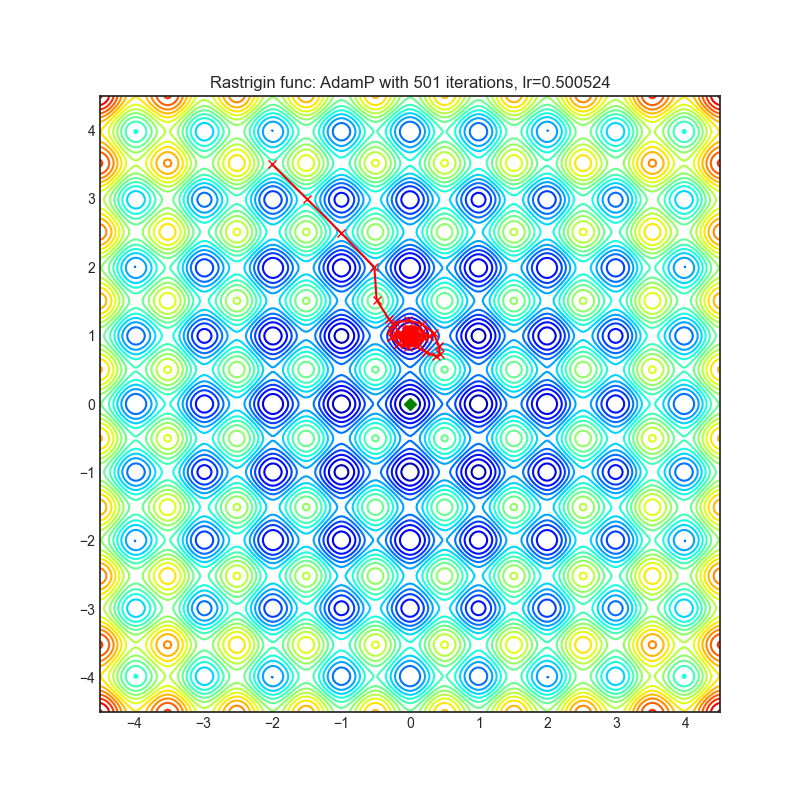
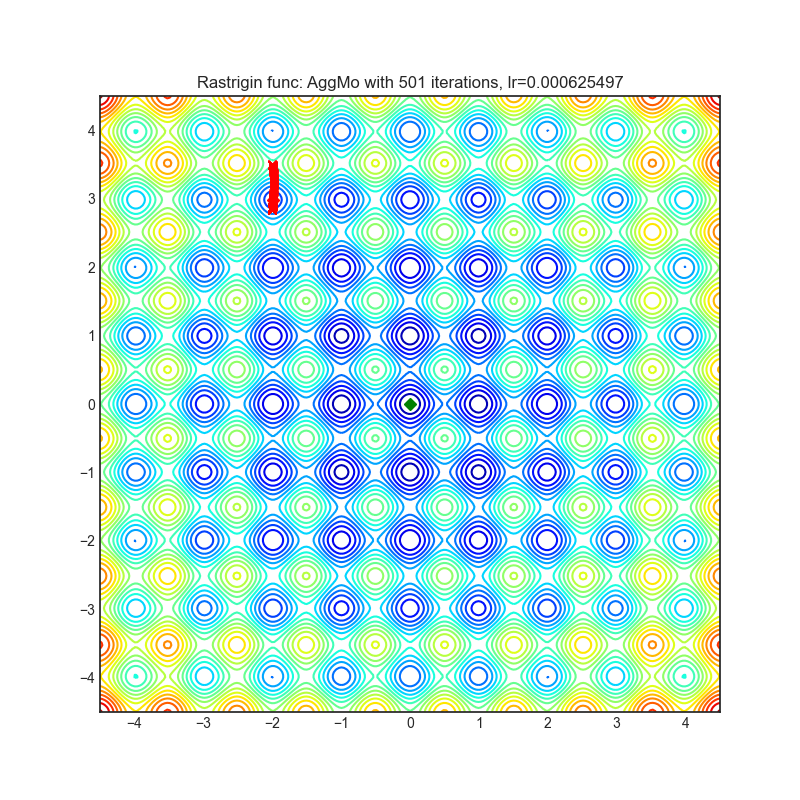
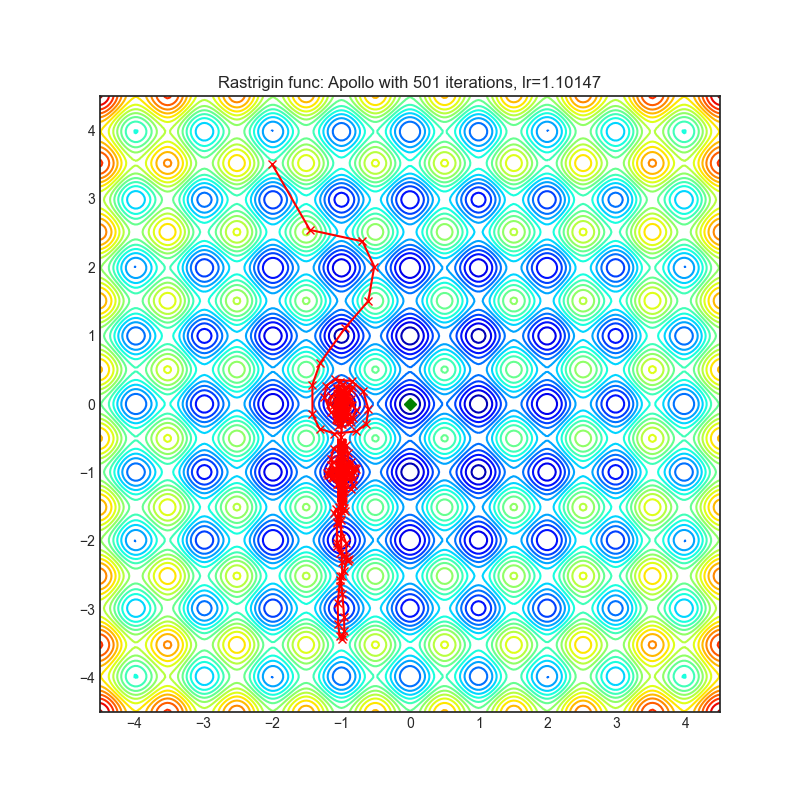
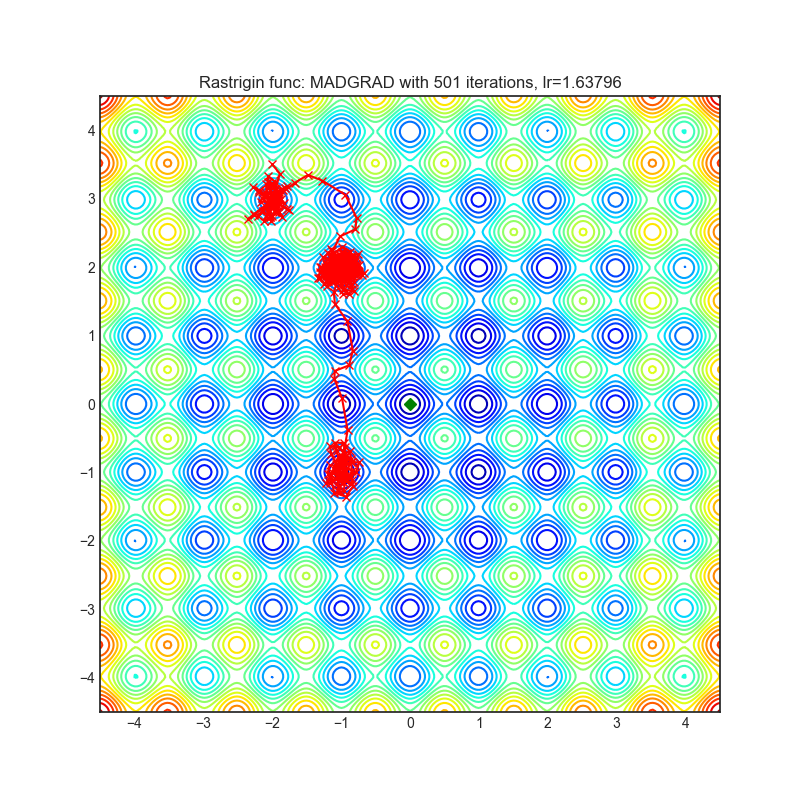
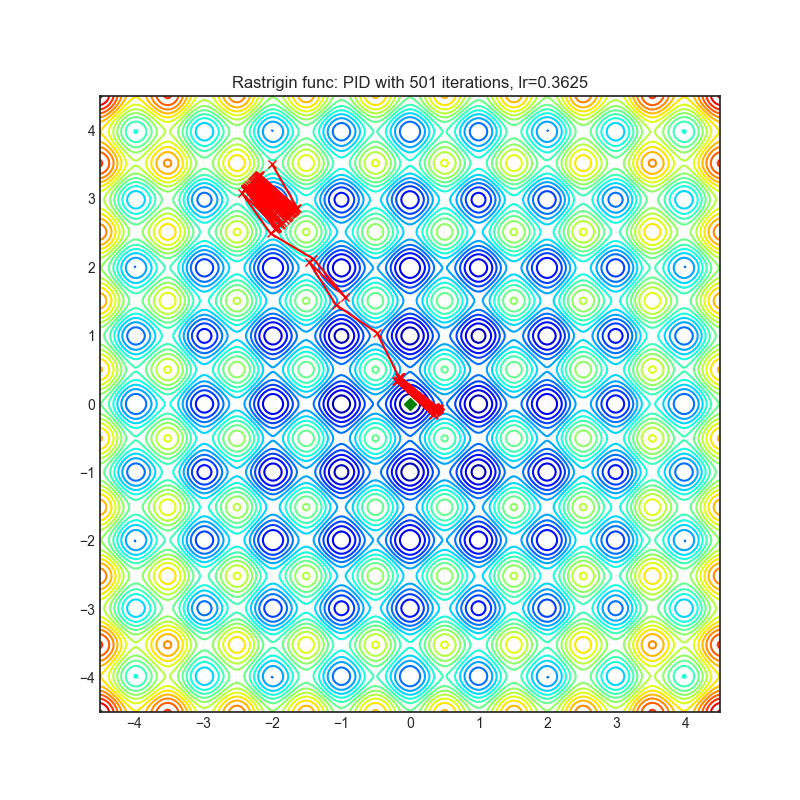
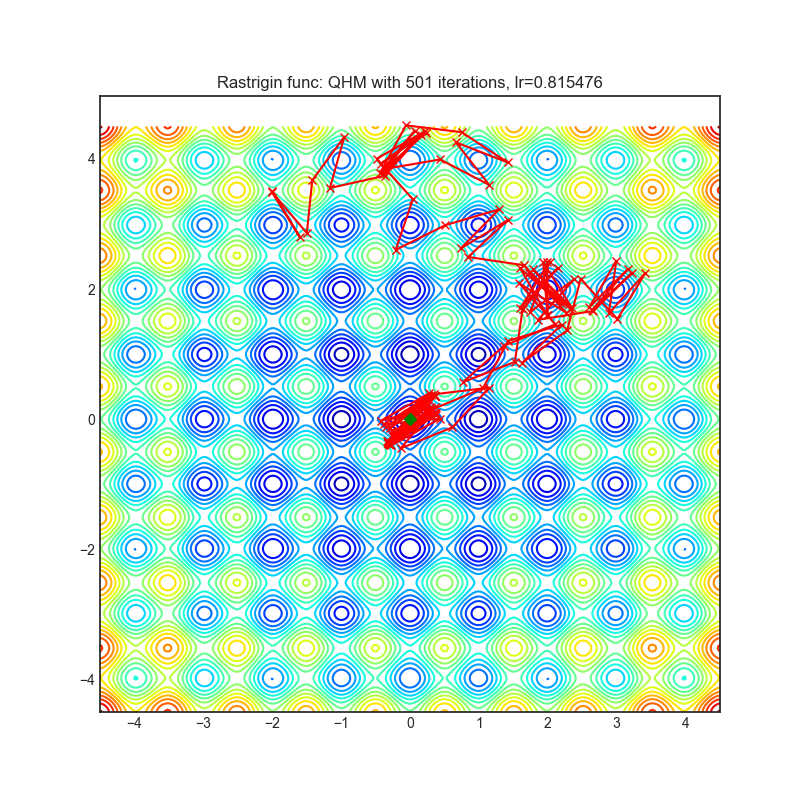
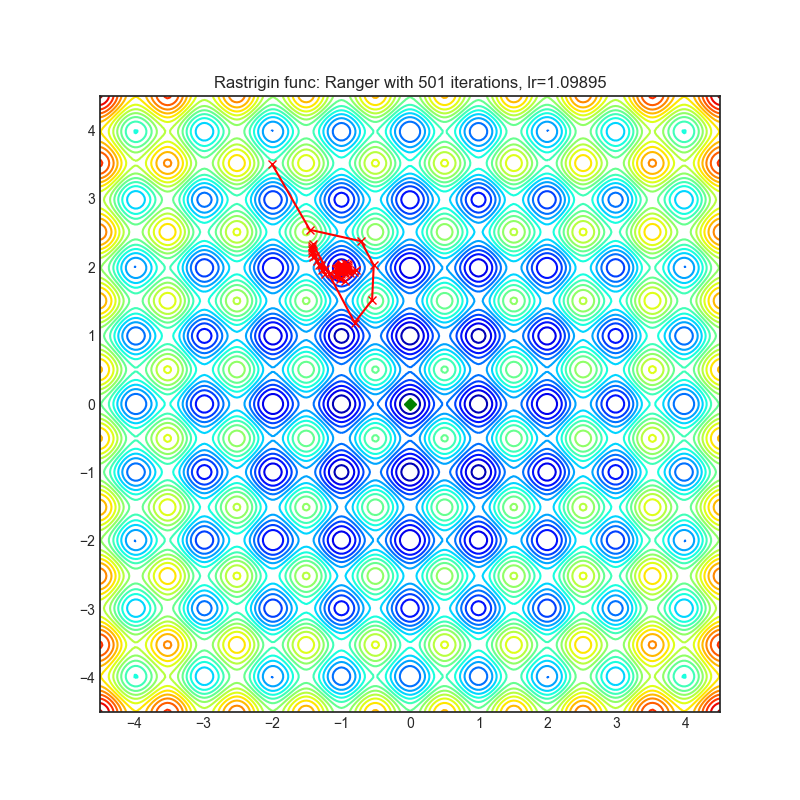
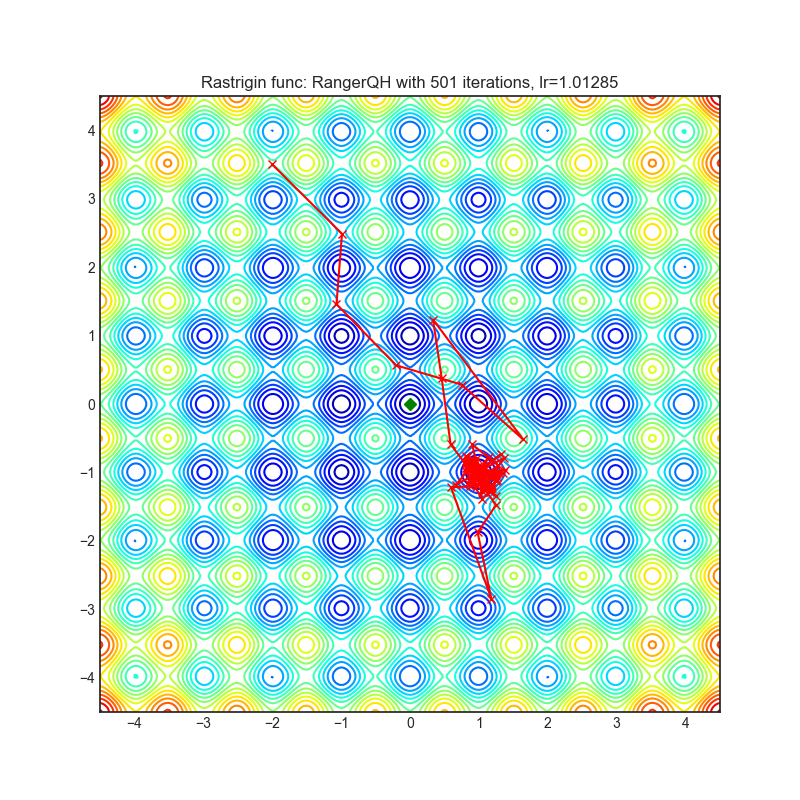
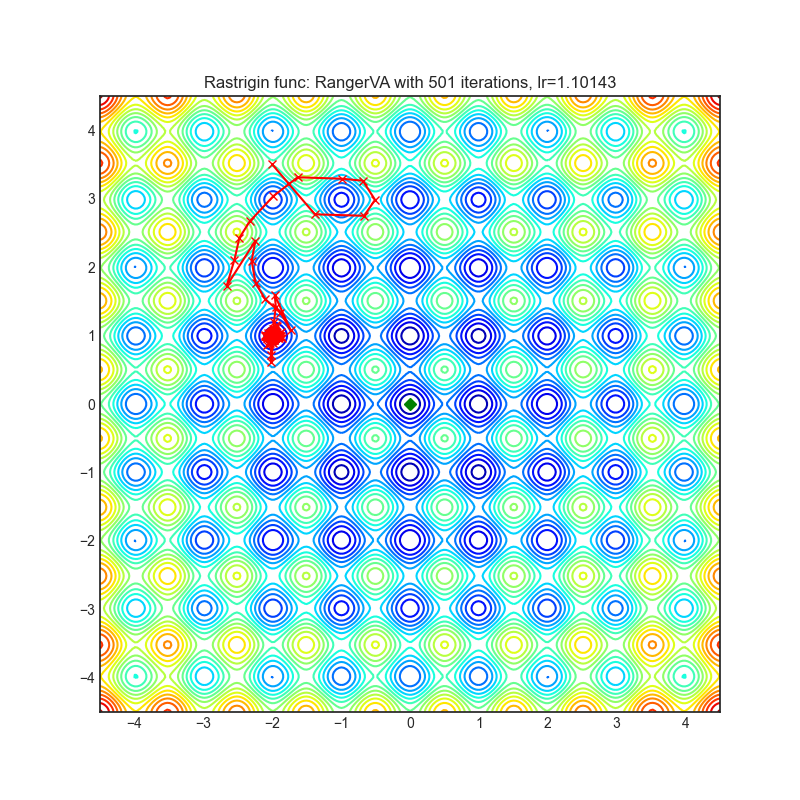
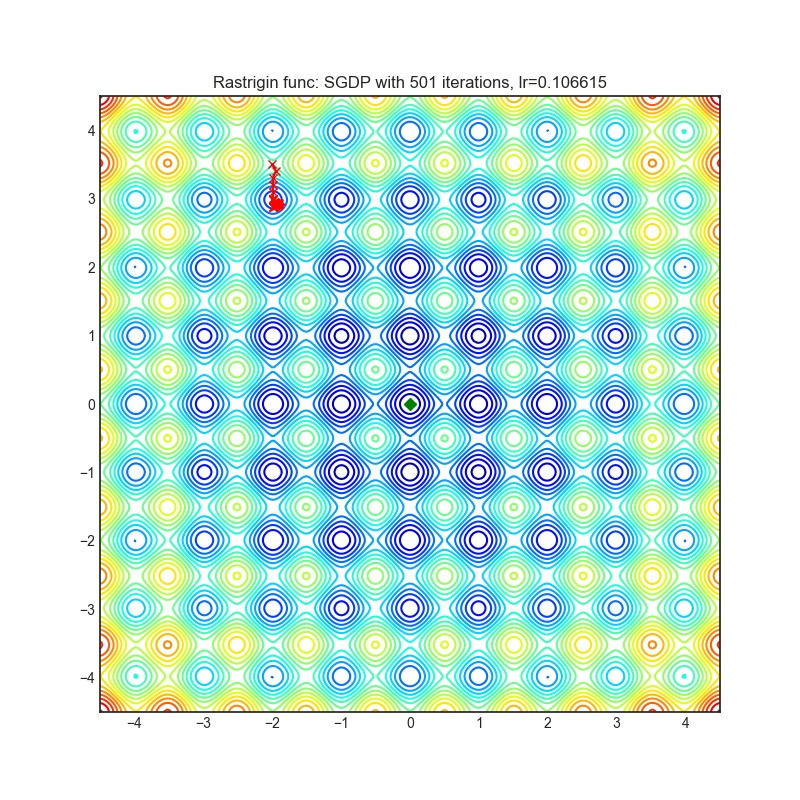
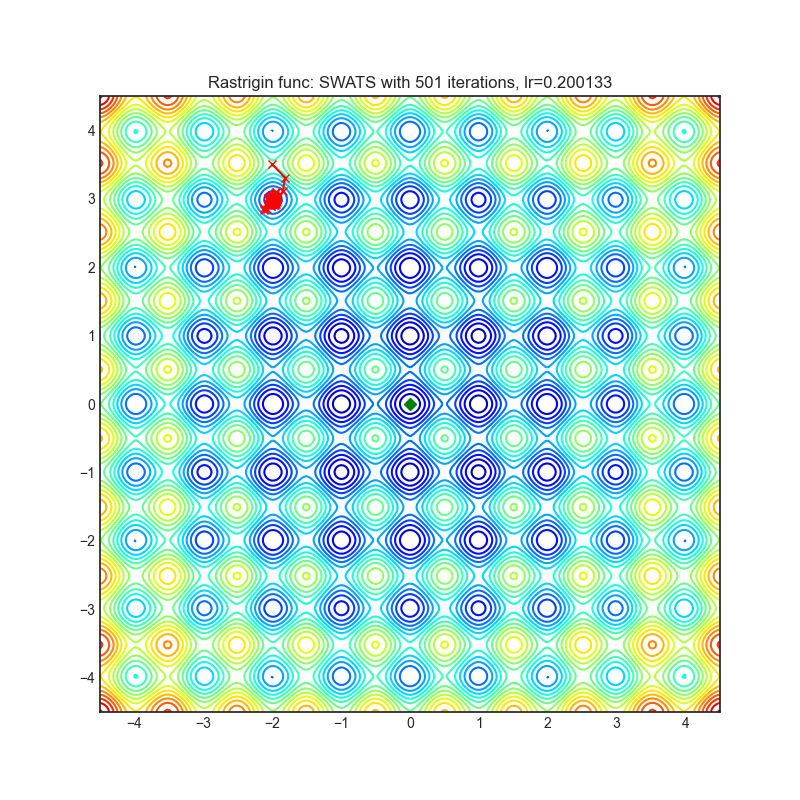
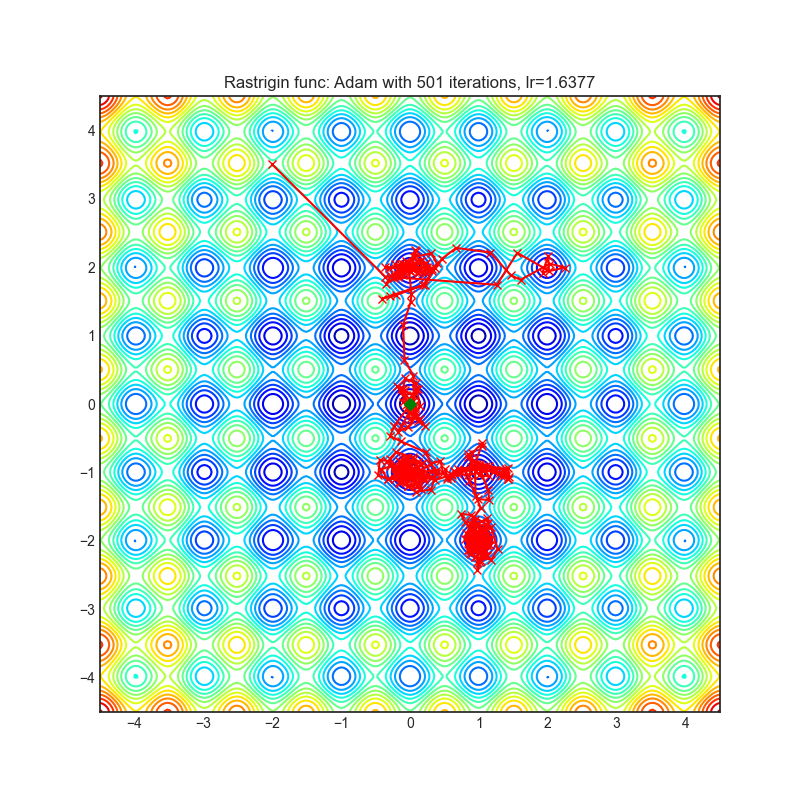
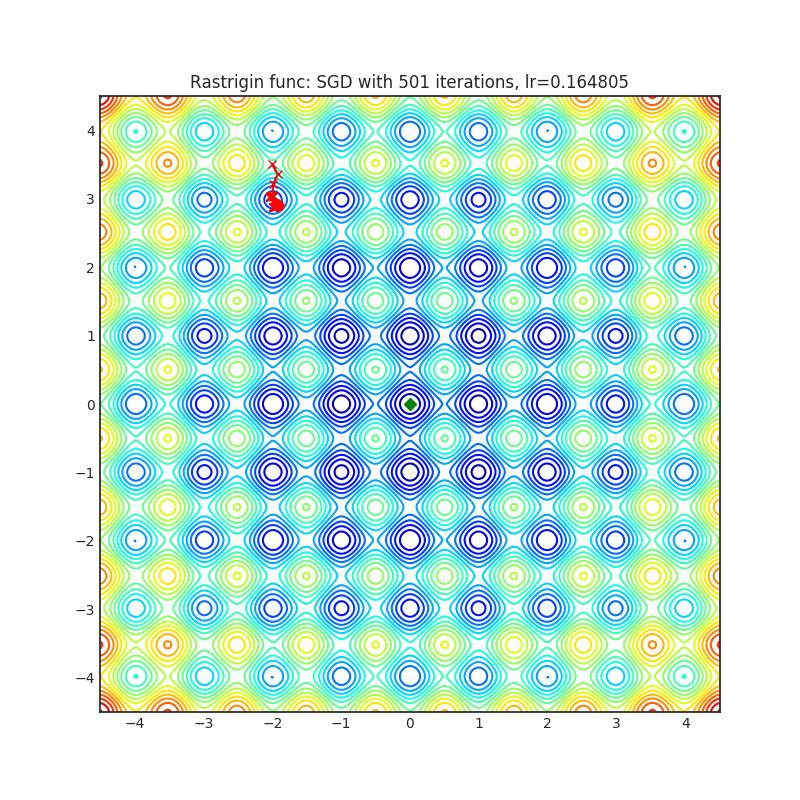
• Rastrigin function is a non-convex and has one global minima in (0.0, 0.0). Finding the minimum of this function is a fairly difficult problem due to its large search space and its large number of local minima.

  

Each optimizer performs 501 optimization steps. Learning rate is best one found by hyper parameter search algorithm, rest of tuning parameters are default. It is very easy to extend script and tune other optimizer parameters.

python examples/viz_optimizers.py

Warning

Do not pick optimizer based on visualizations, optimization approaches have unique properties and may be tailored for different purposes or may require explicit learning rate schedule etc. Best way to find out, is to try one on your particular problem and see if it improves scores.

If you do not know which optimizer to use start with built in SGD/Adam, once training logic is ready and baseline scores are established, swap optimizer and see if there is any improvement.

A2GradExp

import torch_optimizer as optim

# model = ...
optimizer = optim.A2GradExp(
    model.parameters(),
    kappa=1000.0,
    beta=10.0,
    lips=10.0,
    rho=0.5,
)
optimizer.step()

Paper: Optimal Adaptive and Accelerated Stochastic Gradient Descent (2018) [https://arxiv.org/abs/1810.00553]

Reference Code: https://github.com/severilov/A2Grad_optimizer

A2GradInc

import torch_optimizer as optim

# model = ...
optimizer = optim.A2GradInc(
    model.parameters(),
    kappa=1000.0,
    beta=10.0,
    lips=10.0,
)
optimizer.step()

Paper: Optimal Adaptive and Accelerated Stochastic Gradient Descent (2018) [https://arxiv.org/abs/1810.00553]

Reference Code: https://github.com/severilov/A2Grad_optimizer

A2GradUni

import torch_optimizer as optim

# model = ...
optimizer = optim.A2GradUni(
    model.parameters(),
    kappa=1000.0,
    beta=10.0,
    lips=10.0,
)
optimizer.step()

Paper: Optimal Adaptive and Accelerated Stochastic Gradient Descent (2018) [https://arxiv.org/abs/1810.00553]

Reference Code: https://github.com/severilov/A2Grad_optimizer

AccSGD

import torch_optimizer as optim

# model = ...
optimizer = optim.AccSGD(
    model.parameters(),
    lr=1e-3,
    kappa=1000.0,
    xi=10.0,
    small_const=0.7,
    weight_decay=0
)
optimizer.step()

Paper: On the insufficiency of existing momentum schemes for Stochastic Optimization (2019) [https://arxiv.org/abs/1803.05591]

Reference Code: https://github.com/rahulkidambi/AccSGD

AdaBelief

import torch_optimizer as optim

# model = ...
optimizer = optim.AdaBelief(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-3,
    weight_decay=0,
    amsgrad=False,
    weight_decouple=False,
    fixed_decay=False,
    rectify=False,
)
optimizer.step()

Paper: AdaBelief Optimizer, adapting stepsizes by the belief in observed gradients (2020) [https://arxiv.org/abs/2010.07468]

Reference Code: https://github.com/juntang-zhuang/Adabelief-Optimizer

AdaBound

import torch_optimizer as optim

# model = ...
optimizer = optim.AdaBound(
    m.parameters(),
    lr= 1e-3,
    betas= (0.9, 0.999),
    final_lr = 0.1,
    gamma=1e-3,
    eps= 1e-8,
    weight_decay=0,
    amsbound=False,
)
optimizer.step()

Paper: Adaptive Gradient Methods with Dynamic Bound of Learning Rate (2019) [https://arxiv.org/abs/1902.09843]

Reference Code: https://github.com/Luolc/AdaBound

AdaMod

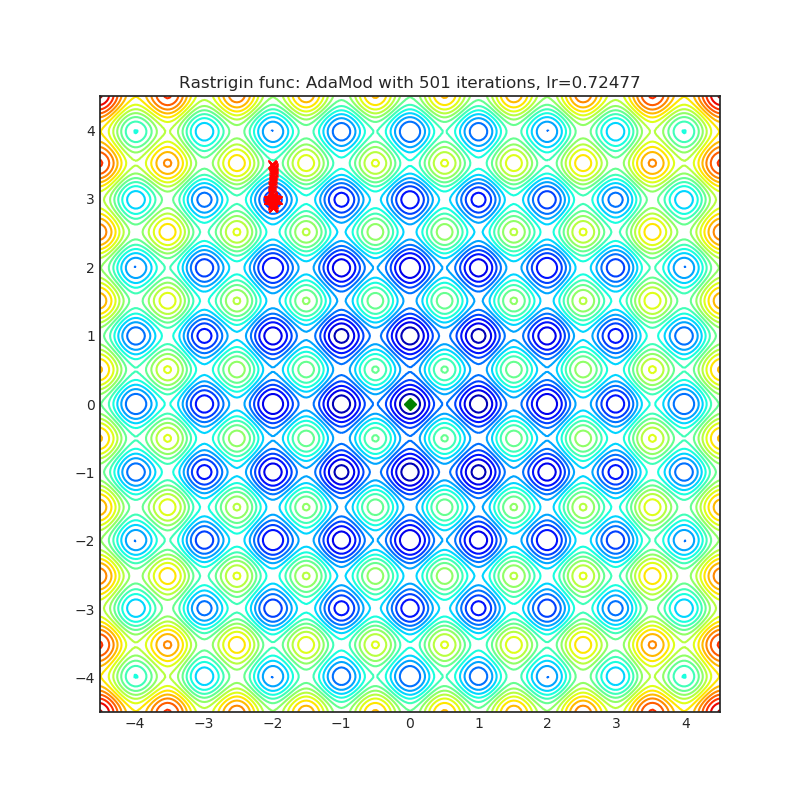
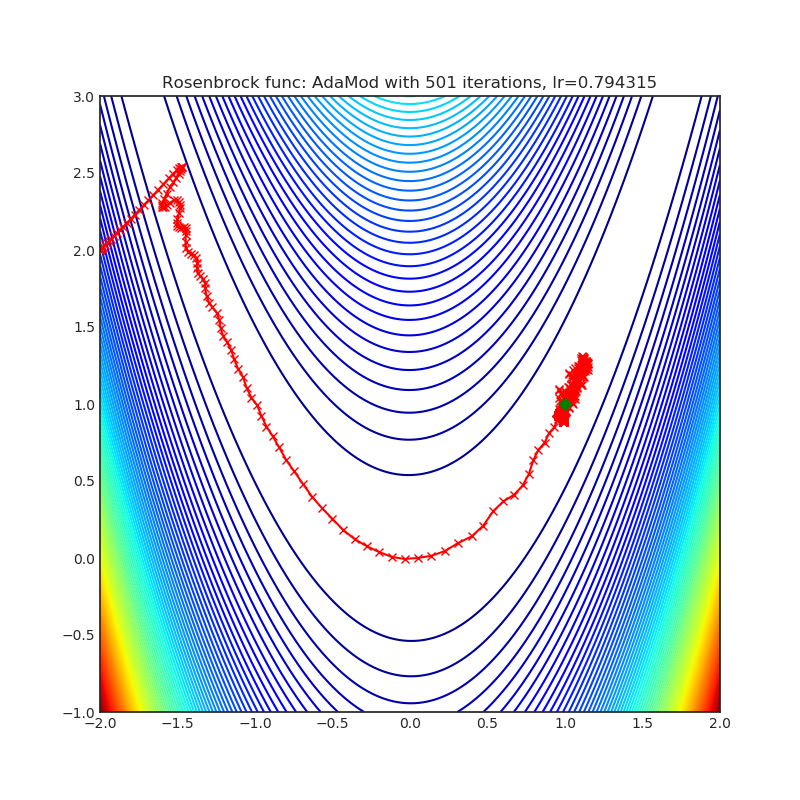
AdaMod method restricts the adaptive learning rates with adaptive and momental upper bounds. The dynamic learning rate bounds are based on the exponential moving averages of the adaptive learning rates themselves, which smooth out unexpected large learning rates and stabilize the training of deep neural networks.

import torch_optimizer as optim

# model = ...
optimizer = optim.AdaMod(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    beta3=0.999,
    eps=1e-8,
    weight_decay=0,
)
optimizer.step()

Paper: An Adaptive and Momental Bound Method for Stochastic Learning. (2019) [https://arxiv.org/abs/1910.12249]

Reference Code: https://github.com/lancopku/AdaMod

Adafactor

import torch_optimizer as optim

# model = ...
optimizer = optim.Adafactor(
    m.parameters(),
    lr= 1e-3,
    eps2= (1e-30, 1e-3),
    clip_threshold=1.0,
    decay_rate=-0.8,
    beta1=None,
    weight_decay=0.0,
    scale_parameter=True,
    relative_step=True,
    warmup_init=False,
)
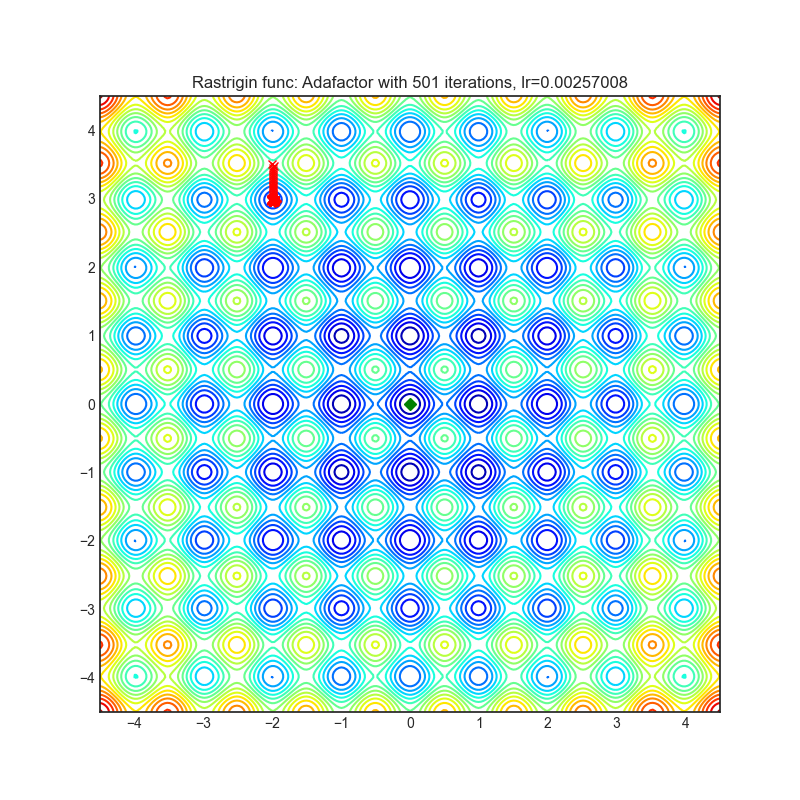
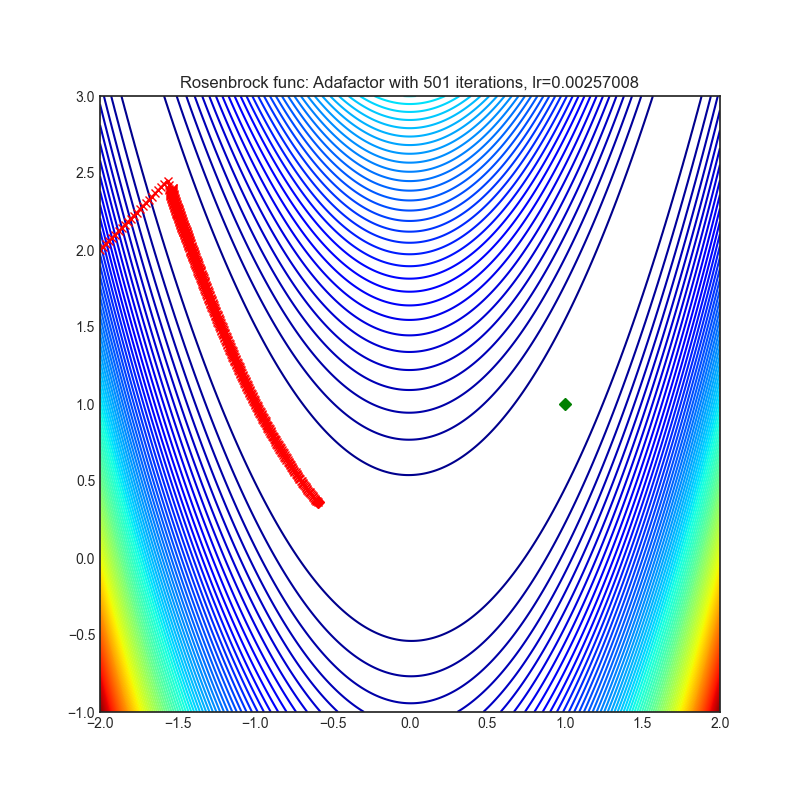
optimizer.step()

Paper: Adafactor: Adaptive Learning Rates with Sublinear Memory Cost. (2018) [https://arxiv.org/abs/1804.04235]

Reference Code: https://github.com/pytorch/fairseq/blob/master/fairseq/optim/adafactor.py

Adahessian

import torch_optimizer as optim

# model = ...
optimizer = optim.Adahessian(
    m.parameters(),
    lr= 1.0,
    betas= (0.9, 0.999),
    eps= 1e-4,
    weight_decay=0.0,
    hessian_power=1.0,
)
      loss_fn(m(input), target).backward(create_graph = True) # create_graph=True is necessary for Hessian calculation
optimizer.step()

Paper: ADAHESSIAN: An Adaptive Second Order Optimizer for Machine Learning (2020) [https://arxiv.org/abs/2006.00719]

Reference Code: https://github.com/amirgholami/adahessian

AdamP

AdamP propose a simple and effective solution: at each iteration of Adam optimizer applied on scale-invariant weights (e.g., Conv weights preceding a BN layer), AdamP remove the radial component (i.e., parallel to the weight vector) from the update vector. Intuitively, this operation prevents the unnecessary update along the radial direction that only increases the weight norm without contributing to the loss minimization.

import torch_optimizer as optim

# model = ...
optimizer = optim.AdamP(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-8,
    weight_decay=0,
    delta = 0.1,
    wd_ratio = 0.1
)
optimizer.step()

Paper: Slowing Down the Weight Norm Increase in Momentum-based Optimizers. (2020) [https://arxiv.org/abs/2006.08217]

Reference Code: https://github.com/clovaai/AdamP

AggMo

import torch_optimizer as optim

# model = ...
optimizer = optim.AggMo(
    m.parameters(),
    lr= 1e-3,
    betas=(0.0, 0.9, 0.99),
    weight_decay=0,
)
optimizer.step()

Paper: Aggregated Momentum: Stability Through Passive Damping. (2019) [https://arxiv.org/abs/1804.00325]

Reference Code: https://github.com/AtheMathmo/AggMo

Apollo

import torch_optimizer as optim

# model = ...
optimizer = optim.Apollo(
    m.parameters(),
    lr= 1e-2,
    beta=0.9,
    eps=1e-4,
    warmup=0,
    init_lr=0.01,
    weight_decay=0,
)
optimizer.step()

Paper: Apollo: An Adaptive Parameter-wise Diagonal Quasi-Newton Method for Nonconvex Stochastic Optimization. (2020) [https://arxiv.org/abs/2009.13586]

Reference Code: https://github.com/XuezheMax/apollo

DiffGrad

Optimizer based on the difference between the present and the immediate past gradient, the step size is adjusted for each parameter in such a way that it should have a larger step size for faster gradient changing parameters and a lower step size for lower gradient changing parameters.

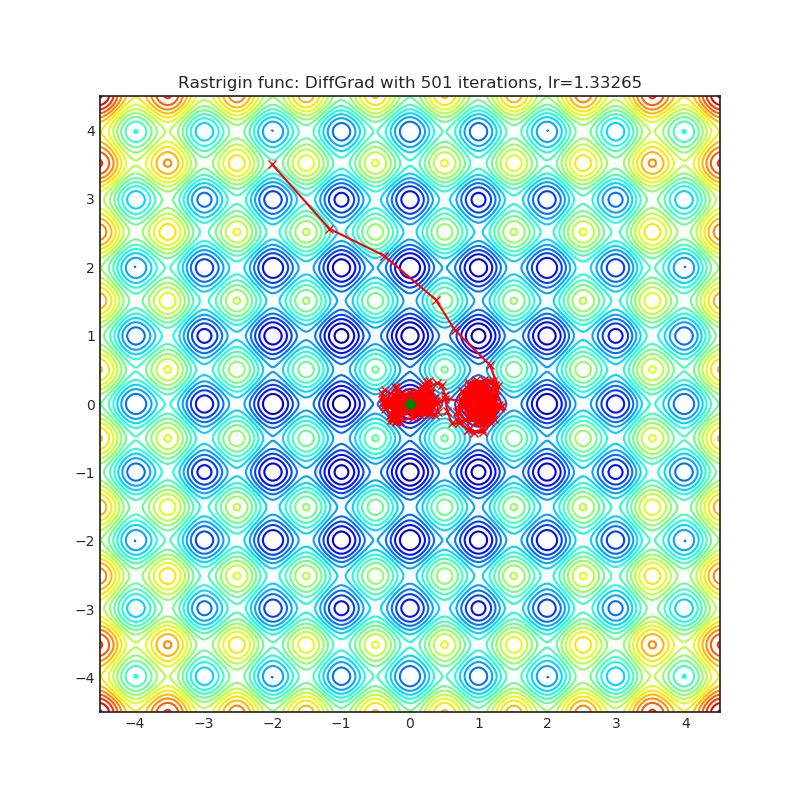
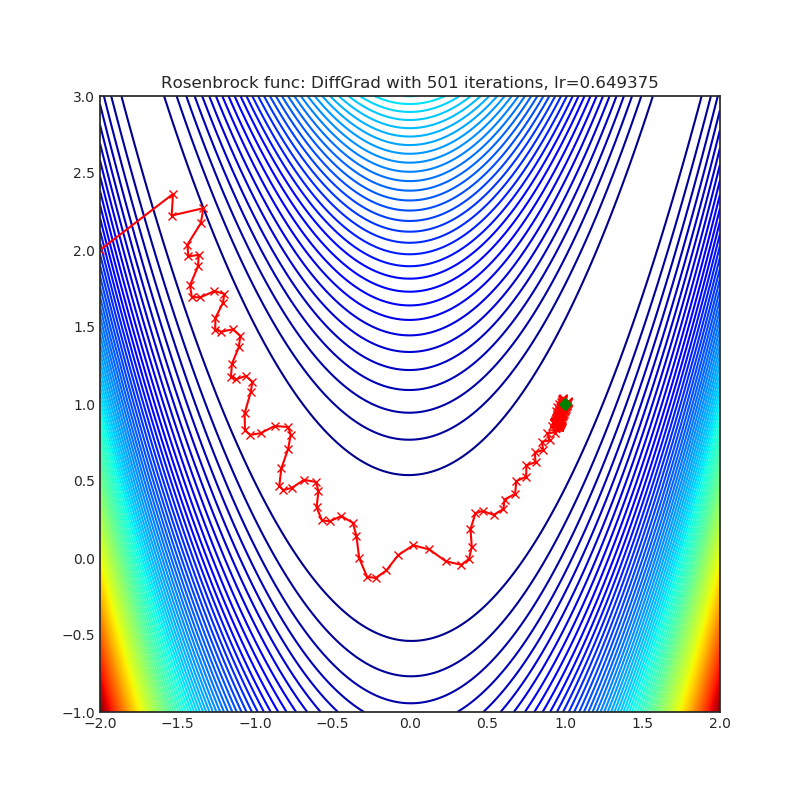
import torch_optimizer as optim

# model = ...
optimizer = optim.DiffGrad(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-8,
    weight_decay=0,
)
optimizer.step()

Paper: diffGrad: An Optimization Method for Convolutional Neural Networks. (2019) [https://arxiv.org/abs/1909.11015]

Reference Code: https://github.com/shivram1987/diffGrad

Lamb

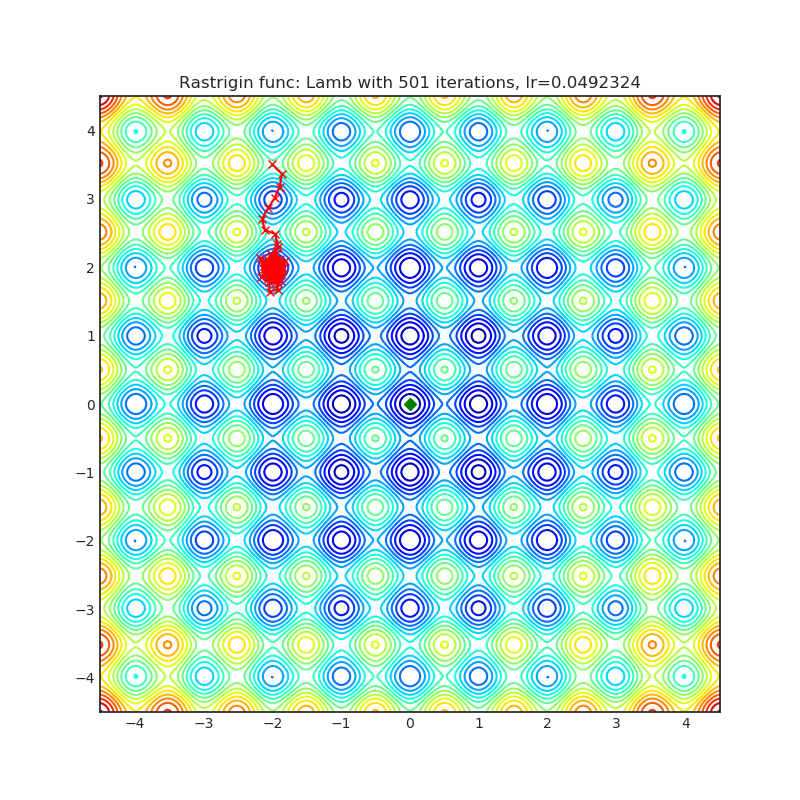
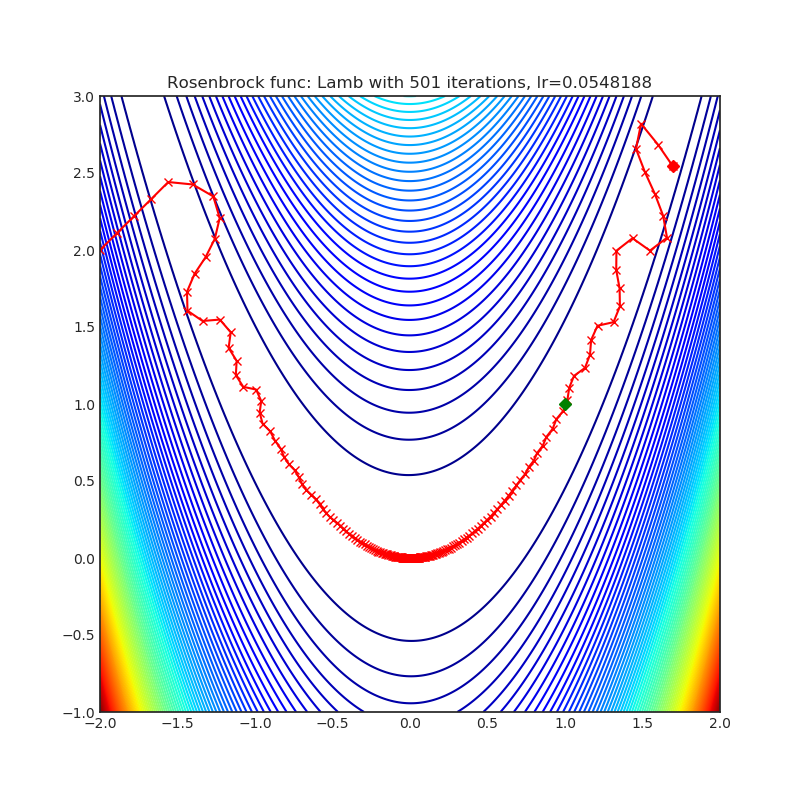
import torch_optimizer as optim

# model = ...
optimizer = optim.Lamb(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-8,
    weight_decay=0,
)
optimizer.step()

Paper: Large Batch Optimization for Deep Learning: Training BERT in 76 minutes (2019) [https://arxiv.org/abs/1904.00962]

Reference Code: https://github.com/cybertronai/pytorch-lamb

Lookahead

import torch_optimizer as optim

# model = ...
# base optimizer, any other optimizer can be used like Adam or DiffGrad
yogi = optim.Yogi(
    m.parameters(),
    lr= 1e-2,
    betas=(0.9, 0.999),
    eps=1e-3,
    initial_accumulator=1e-6,
    weight_decay=0,
)

optimizer = optim.Lookahead(yogi, k=5, alpha=0.5)
optimizer.step()

Paper: Lookahead Optimizer: k steps forward, 1 step back (2019) [https://arxiv.org/abs/1907.08610]

Reference Code: https://github.com/alphadl/lookahead.pytorch

MADGRAD

import torch_optimizer as optim

# model = ...
optimizer = optim.MADGRAD(
    m.parameters(),
    lr=1e-2,
    momentum=0.9,
    weight_decay=0,
    eps=1e-6,
)
optimizer.step()

Paper: Adaptivity without Compromise: A Momentumized, Adaptive, Dual Averaged Gradient Method for Stochastic Optimization (2021) [https://arxiv.org/abs/2101.11075]

Reference Code: https://github.com/facebookresearch/madgrad

NovoGrad

import torch_optimizer as optim

# model = ...
optimizer = optim.NovoGrad(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-8,
    weight_decay=0,
    grad_averaging=False,
    amsgrad=False,
)
optimizer.step()

Paper: Stochastic Gradient Methods with Layer-wise Adaptive Moments for Training of Deep Networks (2019) [https://arxiv.org/abs/1905.11286]

Reference Code: https://github.com/NVIDIA/DeepLearningExamples/

PID

import torch_optimizer as optim

# model = ...
optimizer = optim.PID(
    m.parameters(),
    lr=1e-3,
    momentum=0,
    dampening=0,
    weight_decay=1e-2,
    integral=5.0,
    derivative=10.0,
)
optimizer.step()

Paper: A PID Controller Approach for Stochastic Optimization of Deep Networks (2018) [http://www4.comp.polyu.edu.hk/~cslzhang/paper/CVPR18_PID.pdf]

Reference Code: https://github.com/tensorboy/PIDOptimizer

QHAdam

import torch_optimizer as optim

# model = ...
optimizer = optim.QHAdam(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    nus=(1.0, 1.0),
    weight_decay=0,
    decouple_weight_decay=False,
    eps=1e-8,
)
optimizer.step()

Paper: Quasi-hyperbolic momentum and Adam for deep learning (2019) [https://arxiv.org/abs/1810.06801]

Reference Code: https://github.com/facebookresearch/qhoptim

QHM

import torch_optimizer as optim

# model = ...
optimizer = optim.QHM(
    m.parameters(),
    lr=1e-3,
    momentum=0,
    nu=0.7,
    weight_decay=1e-2,
    weight_decay_type='grad',
)
optimizer.step()

Paper: Quasi-hyperbolic momentum and Adam for deep learning (2019) [https://arxiv.org/abs/1810.06801]

Reference Code: https://github.com/facebookresearch/qhoptim

RAdam

import torch_optimizer as optim

# model = ...
optimizer = optim.RAdam(
    m.parameters(),
    lr= 1e-3,
    betas=(0.9, 0.999),
    eps=1e-8,
    weight_decay=0,
)
optimizer.step()

Paper: On the Variance of the Adaptive Learning Rate and Beyond (2019) [https://arxiv.org/abs/1908.03265]

Reference Code: https://github.com/LiyuanLucasLiu/RAdam

Ranger

import torch_optimizer as optim

# model = ...
optimizer = optim.Ranger(
    m.parameters(),
    lr=1e-3,
    alpha=0.5,
    k=6,
    N_sma_threshhold=5,
    betas=(.95, 0.999),
    eps=1e-5,
    weight_decay=0
)
optimizer.step()

Paper: New Deep Learning Optimizer, Ranger: Synergistic combination of RAdam + LookAhead for the best of both (2019) [https://medium.com/@lessw/new-deep-learning-optimizer-ranger-synergistic-combination-of-radam-lookahead-for-the-best-of-2dc83f79a48d]

Reference Code: https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer

RangerQH

import torch_optimizer as optim

# model = ...
optimizer = optim.RangerQH(
    m.parameters(),
    lr=1e-3,
    betas=(0.9, 0.999),
    nus=(.7, 1.0),
    weight_decay=0.0,
    k=6,
    alpha=.5,
    decouple_weight_decay=False,
    eps=1e-8,
)
optimizer.step()

Paper: Quasi-hyperbolic momentum and Adam for deep learning (2018) [https://arxiv.org/abs/1810.06801]

Reference Code: https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer

RangerVA

import torch_optimizer as optim

# model = ...
optimizer = optim.RangerVA(
    m.parameters(),
    lr=1e-3,
    alpha=0.5,
    k=6,
    n_sma_threshhold=5,
    betas=(.95, 0.999),
    eps=1e-5,
    weight_decay=0,
    amsgrad=True,
    transformer='softplus',
    smooth=50,
    grad_transformer='square'
)
optimizer.step()

Paper: Calibrating the Adaptive Learning Rate to Improve Convergence of ADAM (2019) [https://arxiv.org/abs/1908.00700v2]

Reference Code: https://github.com/lessw2020/Ranger-Deep-Learning-Optimizer

SGDP

import torch_optimizer as optim

# model = ...
optimizer = optim.SGDP(
    m.parameters(),
    lr= 1e-3,
    momentum=0,
    dampening=0,
    weight_decay=1e-2,
    nesterov=False,
    delta = 0.1,
    wd_ratio = 0.1
)
optimizer.step()

Paper: Slowing Down the Weight Norm Increase in Momentum-based Optimizers. (2020) [https://arxiv.org/abs/2006.08217]

Reference Code: https://github.com/clovaai/AdamP

SGDW

import torch_optimizer as optim

# model = ...
optimizer = optim.SGDW(
    m.parameters(),
    lr= 1e-3,
    momentum=0,
    dampening=0,
    weight_decay=1e-2,
    nesterov=False,
)
optimizer.step()

Paper: SGDR: Stochastic Gradient Descent with Warm Restarts (2017) [https://arxiv.org/abs/1608.03983]

Reference Code: pytorch/pytorch#22466

SWATS

import torch_optimizer as optim

# model = ...
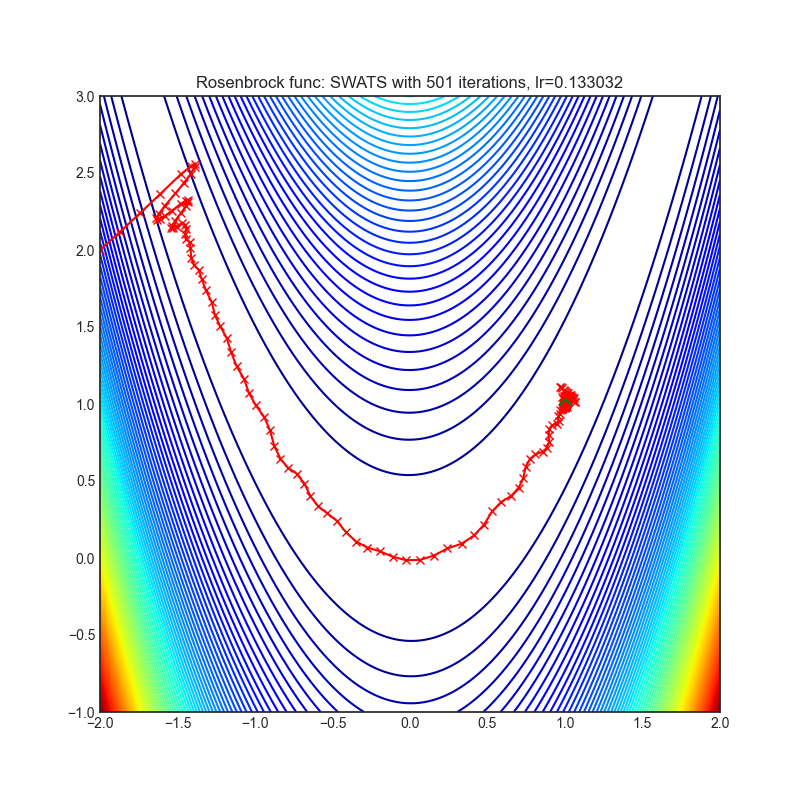
optimizer = optim.SWATS(
    model.parameters(),
    lr=1e-1,
    betas=(0.9, 0.999),
    eps=1e-3,
    weight_decay= 0.0,
    amsgrad=False,
    nesterov=False,
)
optimizer.step()

Paper: Improving Generalization Performance by Switching from Adam to SGD (2017) [https://arxiv.org/abs/1712.07628]

Reference Code: https://github.com/Mrpatekful/swats

Shampoo

import torch_optimizer as optim

# model = ...
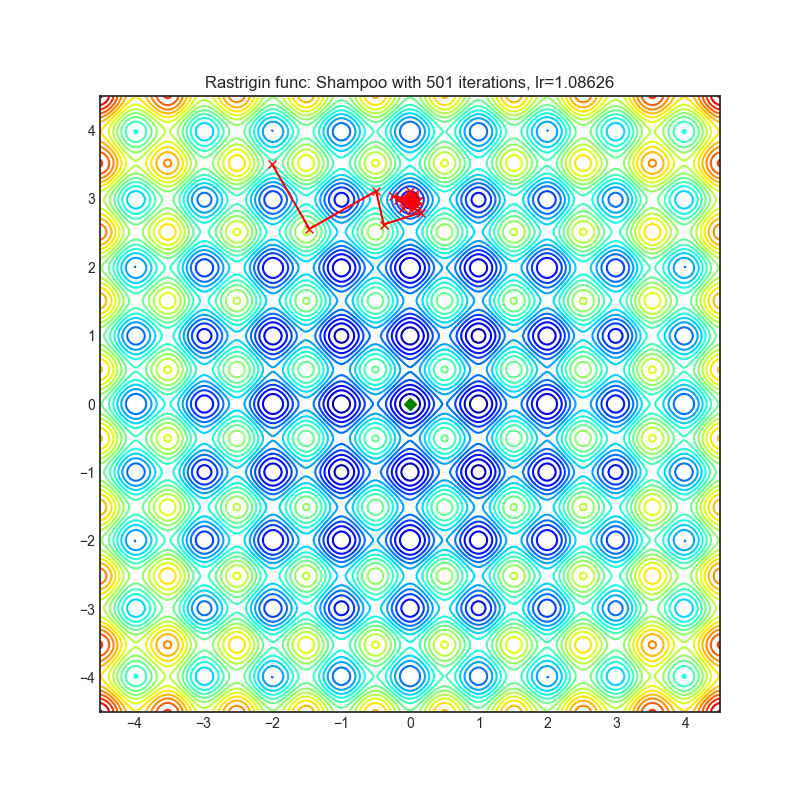
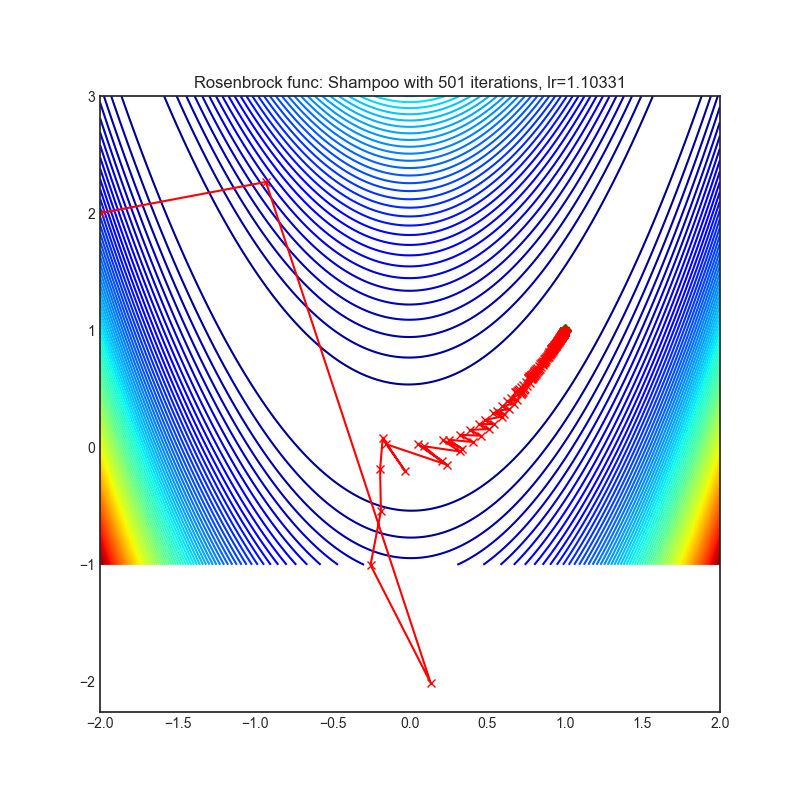
optimizer = optim.Shampoo(
    m.parameters(),
    lr=1e-1,
    momentum=0.0,
    weight_decay=0.0,
    epsilon=1e-4,
    update_freq=1,
)
optimizer.step()

Paper: Shampoo: Preconditioned Stochastic Tensor Optimization (2018) [https://arxiv.org/abs/1802.09568]

Reference Code: https://github.com/moskomule/shampoo.pytorch

Yogi

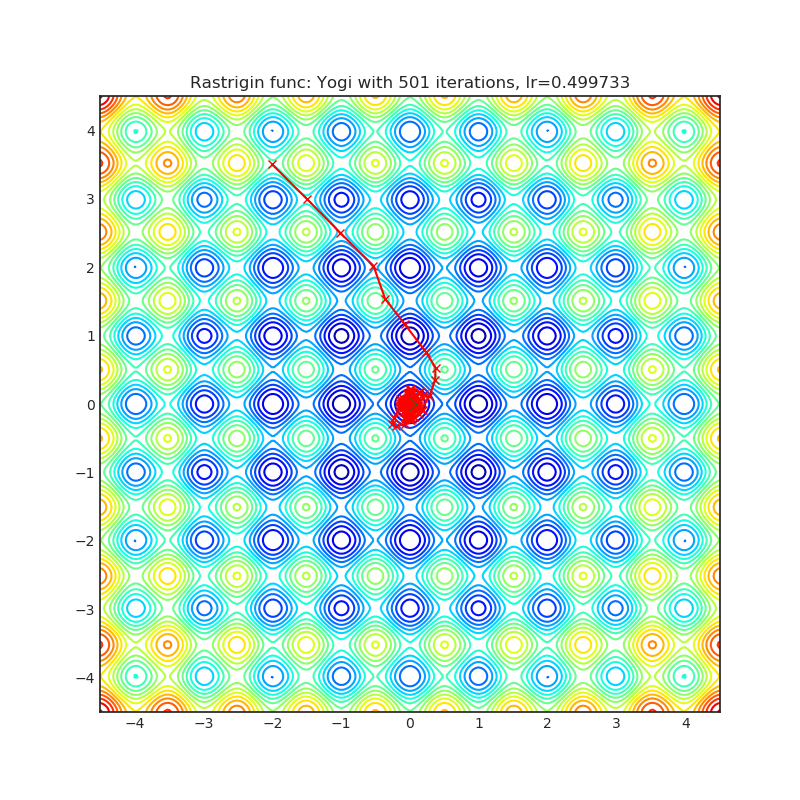
Yogi is optimization algorithm based on ADAM with more fine grained effective learning rate control, and has similar theoretical guarantees on convergence as ADAM.

import torch_optimizer as optim

# model = ...
optimizer = optim.Yogi(
    m.parameters(),
    lr= 1e-2,
    betas=(0.9, 0.999),
    eps=1e-3,
    initial_accumulator=1e-6,
    weight_decay=0,
)
optimizer.step()

Paper: Adaptive Methods for Nonconvex Optimization (2018) [https://papers.nips.cc/paper/8186-adaptive-methods-for-nonconvex-optimization]

Reference Code: https://github.com/4rtemi5/Yogi-Optimizer_Keras

Adam (PyTorch built-in)

SGD (PyTorch built-in)