[TOC]
在每轮迭代时,BGD计算所有样本的残差平方和,然后计算梯度并更新参数,结束本轮迭代。也就是说BGD算法中,每完成一轮迭代(观测完所有的训练样本)只能进行一次参数更新。
对应的算法伪代码:
for it in range(1000): # 1000次迭代
params_grad = evaluate_grad(loss_function, data)
params := params - learning_rate * params SGD每观测到一条数据,都会进行一次参数更新,当完成一轮迭代时,参数已经更新了m次(假设训练样本的样本容量为m,相比于BGD,SGD参数更新的速度更快。
对应的算法伪代码:
for it in range(1000): # 1000次迭代
shuffle(data)
for (x_i, y_i) in data: # 观测所有训练样本
params_grad = evaluate_grad(loss_function, x_i, y_i)
params := params - learning_rate * params | 算法 | 优点 | 缺点 |
|---|---|---|
| BGD | 每次都向着整体最优化方向 | 参数更新比较慢,训练速度慢 |
| SGD | 参数更新比较频繁,训练速度快,但会造成 cost function 有严重的震荡 | SGD的噪音较BGD要多,使得SGD并不是每次都向着整体最优化方向 |
BGD 可能会收敛到local minimal,当然 SGD 的震荡可能会跳出local minimal。
为了平衡训练时模型收敛的速度和收敛的稳定性,同时又能够充分利用深度学习库中高度优化的矩阵操作进行梯度计算,我们每一次采用n个样本进行计算,更新参数。
对应的算法伪代码:
for it in range(1000): # 1000次迭代
shuffle(data)
for mini_batch in get_mini_batch(data): # 观测所有训练样本
params_grad = evaluate_grad(loss_function, mini_batch)
params := params - learning_rate * params 不同特征对应的特征值范围不同,往往这些特征值对应的范围相差很大,例如在做房价预测任务中,房子占地面积(S)这个特征的范围可能是100-200平方米 ,但是房子离最近地铁站的距离(L)可能在5000-10000米之间,两个特征值范围之前的差距很大,这时候就可能会产生一些问题:(1)损失函数中L对损失函数的函数值的影响更大,那么模型其实就潜在假设,相比于S特征,L特征对房价的影响程度更大。但是我们并不想模型会有这样一个偏见,也就是对特征值的差异化对待,我们希望模型训练之后从数据中学习到特征值的差异化,我们希望模型将这个差异化对待体现在参数theta中。(2)模型训练的速度缓慢。例如,在多变量线性回归任务中,将按照以下算法对参数进行更新。 $$ \theta_j:=\theta_j-\alpha\frac {1} {m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{i})x_j ^{i} $$ 由于不同特征值对应的范围空间差异很大,在学习率一定的情况下,范围越大的特征对应的参数更新的速度更快,反之那些范围极小的特征对应的参数更新的速度就很慢。对照下面这张图。
首先看左边这张图,特征x1对应的范围远大于特征x2,也就是相比于x2,x1对损失函数的影响更大,x1对应参数w1的梯度值更大,在进行参数更新时,x1对应参数w1更新的速度更快。由图可以看出,固定w1时,w2的变化对损失函数的函数值影响不是很大,但是在固定w2时,w1的变化对损失函数的函数值影响非常大。所以左边这张图呈现扁平椭圆状,假设选定参数初始值在红线的起点位置,那么红线所画出来的就是参数更新的轨迹(每次朝等高线法向方向移动),参数更新时要走很多弯路,导致参数更新的很慢。反之,右图是我们在预处理中做过Feature Scaling之后,模型训练时参数的更新轨迹,x1特征值和x2特征值对应的范围相当,所以等高线更接近圆形,参数更新时,一直按着圆的半径方向走向loss funciton的global mimal。
将特征值尺度映射到0-1。
\mu是均值,\sigma是方差,将特征值映射到均值是0方差是1的标准高斯分布上。
- 假设函数:
- 损失函数:
$$ \frac {\partial J(\theta)} {\partial\theta_j}=-\frac 1 m \sum_{i=1}^{m}[y^{(i)}\frac {e^{-\theta^Tx^{(i)}}} {1+e^{-\theta^Tx^{(i)}}} x^{(i)}{j} -(1-y^{(i)})\frac 1 {1+e^{-\theta^Tx{(i)}}} x^{(i)}{j}] $$
$$ =-\frac 1 m \sum_{i=1}^{m}[y^{(i)}(1-h_\theta(x^{(i)}))x^{(i)}{j}-(1-y^{(i)})h\theta(x^{(i)})x^{(i)}_{j}] $$
- 参数更新公式:
- 向量化表示:
其中: $$ g(z)=\frac 1 {1+e^{-z}} $$
-
模型会为每个测试样本产生一个实值或概率预测,我们根据这个实值或概率预测将所有测试样本进行排序,“最可能”是正例的测试样本排在最前面,“最不可能”是正例的测试样本排在最后面。然后,在这个排序中选择一个截断点(cut point)或者阈值(threshold),将其分成两部分,前一部分被预测为正例,后一部分被预测为负例。一个好的模型能够将正例和负例区分开,也就是说,从测试样本中随机取一正例样本和一负例样本,一个好的模型能够保证正例样本所对应的实值或概率预测大于负例样本所对应的实值或概率预测。
-
例如,如图为一二分类模型的真实输出结果(已经根据输出的概率值对所有的测试样本进行排序)。
从测试样本中随机选择一个正例和一个负例,正例对应的概率值大于负例对应的概率值这个事件的概率为:
$$ \frac 3 41+\frac 1 4\frac 2 3=\frac {11} {12} $$
-
理解混淆矩阵
在评价分类模型性能的时候,可以使用多个指标,其中查准率(Precision)、查全率(Recall)和F1-Score是分类问题中经常使用的模型评价指标。如图为模型评价时使用到的混淆矩阵(Confusion Matrix)。其中每个统计量代表的含义如下:
• TN:预测值为负(Negative),真实值也为负(Negative),预测正确
• FN:预测值为负(Negative),真实值为正(Positive),预测错误
• FP:预测值为正(Positive),真实值为负(Negative),预测错误
• TP:预测值为正(Positive),真实值也为正(Positive),预测正确
首先,介绍查准率和查全率的计算公式: $$ Precision = \frac {TP} {TP + FP} $$
然后,引入两个概念,True Positive Rate(真阳率)和False Positive Rate(伪阳率): $$ TPRate = \frac {TP} {TP + FN}=\frac {TP} P $$
TPRate的意义是所有真实类别为1的样本中,预测类别为1的比例。
FPRate的意义是所有真实类别为0的样本中,预测类别为1的比例。
-
Why AUC?
ROC曲线的应用场景有很多,根据上述的定义,其最直观的应用就是能反映模型在选取不同阈值的时候其敏感性(sensitivity, FPR)和其精确性(specificity, TPR)的趋势走向。不过,相比于其他的P-R曲线(精确度和召回率),ROC曲线有一个巨大的优势就是,当正负样本的分布发生变化时,其形状能够基本保持不变,而P-R曲线的形状一般会发生剧烈的变化,因此该评估指标能降低不同测试集带来的干扰,更加客观的衡量模型本身的性能。假设负类样本数量扩大十倍,那么FP和TN的数量也会随之增大,这将影响到精确度。但ROC曲线的横纵坐标俩个值,FPRate只考虑第二行(FP和TN),N若增大10倍,则FP、TN也会成比例增加,并不影响其FPRate值,TPRate更是只考虑第一行(TP和FN),不会受到影响。
-
ROC曲线的绘制
该曲线的横坐标是伪阳率,即FPRate,纵坐标为真阳率,即TPRate。
当绘制完成曲线后,就会对模型有一个定性的分析,如果要对模型进行量化的分析,此时需要引入一个新的概念,就是AUC(Area under roc Curve)面积,就是指ROC曲线下的面积大小,而计算AUC值只需要沿着ROC横轴做积分就可以了。真实场景中ROC曲线一般都会在
这条直线的上方,所以AUC的取值一般在0.5~1之间。AUC的值越大,说明该模型的性能越好。
-
ROC曲线绘制实例
采用上文提到的例子,正例样本数P为4,负例样本数N为3。
我们首先将坐标轴X轴[0, 1]区间均分为3(N=3)份,Y轴[0, 1]区间均分为4(P=4)份。
- 当我们设定的阈值很大(例如1.00)时,所有的样本均被识别为负例,那么真阳率TPRate和FPRate均为0,对应于ROC曲线上的(0, 0)一点。
- 当我们适当地降低阈值(例如0.85),那么第一例测试样本会被判为正例,因为第一例测试样本本来就是正例,所以TPRate的值将增大,增大1/P=0.25,对应的(0, 0.25)将落在ROC曲线上。
- 当我们继续降低阈值(例如0.75),那么第二例测试样本会被判为正例,因为第二例测试样本本来就是正例,所以TPRate的值将继续增大,增大1/P=0.25,对应的(0, 0.50)将落在ROC曲线上。
- 继续降低阈值(例如0.65),那么第三例测试样本会被判为正例,因为第三例测试样本本来就是正例,所以TPRate的值将继续增大,增大1/P=0.25,对应的(0, 0.75)将落在ROC曲线上。
- 继续降低阈值(例如0.55),那么第四例测试样本会被判为正例,因为第四例测试样本本来是负例,所以FPRate的值将增大,增大1/N=1/3,对应的(1/3, 0.75)将落在ROC曲线上。
- 继续降低阈值(例如0.45),那么第五例测试样本会被判为正例,因为第五例测试样本本来就是正例,所以TPRate的值将增大,增大1/P=0.25,对应的(1/3, 1.00)将落在ROC曲线上。
- 继续降低阈值(例如0.35),那么第六例测试样本会被判为正例,因为第六例测试样本本来是负例,所以FPRate的值将增大,增大1/N=1/3,对应的(2/3, 1.00)将落在ROC曲线上。
- 继续降低阈值(例如0),那么第七例测试样本会被判为正例,因为第七例测试样本本来是负例,所以FPRate的值将增大,增大1/N=1/3,对应的(1.00, 1.00)将落在ROC曲线上。
根据上述步骤绘出的ROC曲线如图所示:
AUC面积和等于: $$ \frac 3 41+\frac 1 4\frac 2 3=\frac {11} {12} $$ 等于【从测试样本中随机选择一个正例和一个负例,正例对应的概率值大于负例对应的概率值这个事件的概率】。
-
AUC面积的意义
如果两条ROC曲线没有相交,我们可以根据哪条曲线最靠近左上角哪条曲线代表的学习器性能就最好。但是,实际任务中,情况很复杂,如果两条ROC曲线发生了交叉,则很难一般性地断言谁优谁劣。在很多实际应用中,我们往往希望把学习器性能分出个高低来。在此引入AUC面积。
在进行学习器的比较时,若一个学习器的ROC曲线被另一个学习器的曲线完全“包住”,则可断言后者的性能优于前者;若两个学习器的ROC曲线发生交叉,则难以一般性的断言两者孰优孰劣。此时如果一定要进行比较,则比较合理的判断依据是比较ROC曲线下的面积,即AUC(Area Under ROC Curve)。
-
对于AUC物理意义的理解
AUC是 ROC 曲线的面积,其物理意义是从所有正样本中随机挑选一个样本,模型将其预测为正样本的概率是 p1;从所有负样本中随机挑选一个样本,模型将其预测为正样本的概率是 p0。p1>p0的概率就是AUC的值。AUC考虑的是样本预测的排序质量,样本排序越混乱(正例和负例交错在一起,无法区分开),对应的AUC的值越低,模型的泛化性能越低;样本排序越整齐(正例和负例能够明显区分开),对应的AUC的值越高,模型的泛化性能越高。
-
AUC曲线有以下几个特点:
-
如果完全随机地对样本进行分类,那么p1 > p0的概率为0.5,则AUC=0.5。
-
AUC在样本不平衡条件下仍然适用。
例如在反欺诈场景中,假设正常用户为正类(约占99.99%),欺诈用户为负类(约占0.01%),如果使用准确率评估模型性能,那么模型只需要将所有用户都判为正常用户就可以获得99.99%的准确率,但是这显然不能满足我们的需求,无法检测出欺诈用户。这种情况下,如果使用AUC进行评估,因为所有的用户都被判为正类,所以FPRate和TPRate均为1,此时AUC的面积为0.5,从AUC指标可以看出这不是一个好的模型,其接近于随机分类。
-
AUC反应的是模型对于样本的排序能力(根据样本预测为正类的概率来排序)。例如,AUC=0.7,那么从正类样本中随机选择一个样本A,从负类样本中随机选择一个样本B,那么A被预测为正类的概率p1有百分之七十的把握比B被预测为正类的概率p0大。
-
-
一元微积分中导数与微分的关系 $$ y = f(x) $$
$$ df = f'(x)dx $$
-
多元微积分中梯度与微分的关系 $$ y = f(x_1, x_2, \ldots, x_n) $$
$$ df = \sum_{i=1}^{n}\frac{\part{f}}{\part{x_i}}dx_i=\frac{\part{f}^T}{\part{x}}dx \tag 0 $$
第一个等式,全微分公式;第二个等式,全微分等于梯度向量与微分向量的内积
-
假如说将所有的参数排列成一个矩阵,例如 $$ X = \left[\begin{matrix} x_{11} & x_{12} & x_{13} \ x_{21} & x_{22} & x_{23} \end{matrix}\right] $$
$$ df = \frac{\part{f}}{\part{x_{11}}}dx_{11}+\frac{\part{f}}{\part{x_{12}}}dx_{12}+\frac{\part{f}}{\part{x_{13}}}dx_{13}+\frac{\part{f}}{\part{x_{21}}}dx_{21}+\frac{\part{f}}{\part{x_{22}}}dx_{22}+\frac{\part{f}}{\part{x_{23}}}dx_{23} $$
把函数f对所有参数的偏导数,按照参数矩阵X的形状,对应元素对应放置,相应地可以组成一个“偏导数矩阵” $$ \frac{\part{f}}{\part{X}} = \left[\begin{matrix} \frac{\part{f}}{\part{x_{11}}} & \frac{\part{f}}{\part{x_{12}}} & \frac{\part{f}}{\part{x_{13}}} \ \frac{\part{f}}{\part{x_{21}}} & \frac{\part{f}}{\part{x_{22}}} & \frac{\part{f}}{\part{x_{23}}} \end{matrix}\right] $$
$$ \frac{\part{f}^T}{\part{X}}·dX = \left[\begin{matrix} \frac{\part{f}}{\part{x_{11}}} & \frac{\part{f}}{\part{x_{21}}} \ \frac{\part{f}}{\part{x_{12}}} & \frac{\part{f}}{\part{x_{22}}} \ \frac{\part{f}}{\part{x_{13}}} & \frac{\part{f}}{\part{x_{23}}} \end{matrix}\right] . \left[\begin{matrix} dx_{11} & dx_{12} & dx_{13} \ dx_{21} & dx_{22} & dx_{23} \end{matrix}\right] $$
$$ =\left[ \begin{matrix} \frac{\part{f}}{\part{x_{11}}}dx_{11}+\frac{\part{f}}{\part{x_{21}}}dx_{21} & * & * \
- & \frac{\part{f}}{\part{x_{12}}}dx_{12}+\frac{\part{f}}{\part{x_{22}}}dx_{22} & * \
- & * & \frac{\part{f}}{\part{x_{13}}}dx_{13}+\frac{\part{f}}{\part{x_{23}}}dx_{23} \end{matrix} \right] $$
-
所以函数f的全微分可以表示成(tr表示矩阵的迹,tr(A)表示矩阵A主对角元素上所有元素的和): $$ df = tr(\frac{\part{f}^T}{\part{X}}·dX) $$
-
矩阵微分的运算法则
- 加减法:$d(X \pm Y) = d(X) \pm d(Y)$
- 乘法:
$d(XY) = d(X)Y + Xd(Y)$ - 转置:
$d(X^T) = d(X)^T$ - 迹:
$d(tr(X)) = tr(d(X))$ - 逆:
$$ XX^{-1}=I\ d(XX^{-1}) =d(X)X^{-1}+Xd(X^{-1})\ = d(I)\ = 0 $$
$$ d(X^{-1}) = -X^{-1}dXX^{-1} $$
- 逐元素乘法:$d(X\bigodot Y) = dX\bigodot Y+ X\bigodot dY$
- 逐元素函数:$d(\sigma(X)) = \sigma'(X) \bigodot dX $
我们希望通过求出函数f的微分后,通过公式$df = tr(\frac{\part{f}^T}{\part{X}}·dX)$计算矩阵导数
-
迹技巧
-
标量套上迹:
$a = tr(a)$ -
转置:
$tr(A^T) = tr(A)$ -
线性:
$tr(A \pm B) = tr(A) \pm tr(B)$ -
矩阵乘法交换:
$tr(AB) = tr(BA)$ ,前提A与B^T形状相同关于第4点证明: $$ tr(AB) = \sum_{i=1}^{n}(AB){ii} \ = \sum{i=1}^{n}\sum_{j=1}^{n}a_{ij}b_{ji} \ = \sum_{j=1}^{n}\sum_{i=1}^{n}b_{ji}a_{ij} \ = tr(BA) $$
-
矩阵乘法,逐元素乘法交换 $$ tr(A^T(B\bigodot C))=\sum_{i,j}^{n}A_{ij}B_{ij}C_{ij}=tr((A\bigodot B)^TC) $$
-
-
复合函数
y = f(Y), Y = g(X)
假设我们已知$\frac {\part{f}} {\part{Y}}
$,如何求$ \frac {\part f} {\part X}$我们先用Y来表示f的全微分,然后再用$X$来表示微分$dY$ $$ df = tr(\frac{\part{f}^T}{\part{Y}}·dY) $$ 例如,当Y = AXB时(A和B是常量) $$ df = tr(\frac{\part{f}^T}{\part{Y}}·dY)\ = tr(\frac{\part{f}^T}{\part{Y}}·AdXB)\ = tr(B\frac{\part{f}^T}{\part{Y}}·AdX) \ = tr((A^T\frac{\part{f}^T}{\part{Y}}B^T)^TdX) $$ 得到 $$ \frac {\part f} {\part X} = A^T\frac{\part{f}^T}{\part{Y}}B^T $$
-
例子
-
$f = a^TXb$ ,另外shape(a) = m×1,shape(X) = m×n,shape(b) = n×1,a和b均为常量,求$\frac {\part f} {\part X}$?解: $$ df = d(a^TXb)\ = d(a^T)Xb + a^TdXb + a^TXd(b)\ = a^TdXb $$ 因为$df$是标量,所以$df=tr(df)$ $$ df = tr(df) = tr(a^TdXb)\ =tr(ba^TdX)\ =tr((ab^T)^TdX) $$ 对照$df = tr(\frac{\part{f}^T}{\part{X}}·dX)$得到$\frac {\part f} {\part X} = ab^T$
-
线性回归$L = ||X\omega-y||^2\$,求$\omega$的最小二乘估计,其中$y$是m×1维向量,$X$是m×n维,$\omega$是n×1维,L是标量 $$ L = ||X\omega-y||^2\ = (X\omega-y)^T(X\omega-y) \tag 1 $$
$$ dL = d(X\omega-y)^T(X\omega-y)+(X\omega-y)^Td(X\omega-y) \ \tag 2 = d(X\omega)^T(X\omega-y)+(X\omega-y)^TXd\omega \ = (d(Xw))^T(X\omega-y)+(X\omega-y)^TXd\omega \ = (Xd\omega)^T(X\omega-y)+(X\omega-y)^TXd\omega \ = 2(X\omega-y)^TXd\omega $$
因为$\omega$是向量(不是矩阵),根据本节中的公式0可得: $$ \frac {\part L} {\part w}^T = 2(X\omega-y)^TX \Rightarrow \frac {\part L} {\part w} = 2X^T(X\omega-y) $$ 令$\frac {\part L} {\part w}$=0得: $$ 2X^T(X\omega-y)=0 \ \Downarrow \ X^TX\omega-X^Ty = 0 \ \Downarrow \ \omega = (X^TX)^{-1}·(X^Ty) $$
-
$f = a^Te^{Xb}$ ,shape(a)=m×1,shape(X)=m×n,shape(b)=n×1,$f$是标量,求$\frac {\part f} {\part X}$ $$ df = d(a^Te^{Xb}) \ = a^Td(e^{Xb}) \ = a^T((e^{Xb})\bigodot (dXb)) \ = tr(a^T((e^{Xb})\bigodot (dXb))) \ = tr((a \bigodot e^{Xb})^Td(Xb)) \ = tr((a \bigodot e^{Xb})^TdXb) \ = tr(b(a \bigodot e^{Xb})^TdX) \ = tr(((a \bigodot e^{Xb}) b^T)^TdX) \ $$$\therefore \frac {\part f} {\part X}=(a \bigodot e^{Xb}) b^T$
-
-
参考:
-
分享:
- Author:
Cl´ement Rebuffel, Laure Soulier, Geoffrey Scoutheeten, and Patrick Gallinari
- Abstract:
将结构化数据转录为自然语言描述已成为一项具有挑战性的任务,称为“数据到文本”。这些结构通常会重新组合多个元素及其属性。大多数尝试都依赖于将元素线性化为序列的翻译的编码器/解码器方法。但是,这丢失了大多数数据中包含的结构信息。在这项工作中,我们提出使用分层模型来克服此限制,该模型在元素级别和结构级别对数据结构进行编码。在RotoWire数据集上的评估显示了我们模型w.r.t.在定性和定量指标上的有效性。
- Why:
一方面,目前大多数的研究工作都是集中在解码器部分,对于数据仅仅是简单地线性化处理。 另一方面,大多数在编码器部分采用RNN(包括GRU和LSTM),这就需要顺序输入数据,这种编码无序数据的方式影响了学习效果。
- What:
Encoder:a two-level Transformer architecture with key-guided hierarchical attention
Decoder:a two-layers LSTM network with a copy mechanism [引用]
- How:
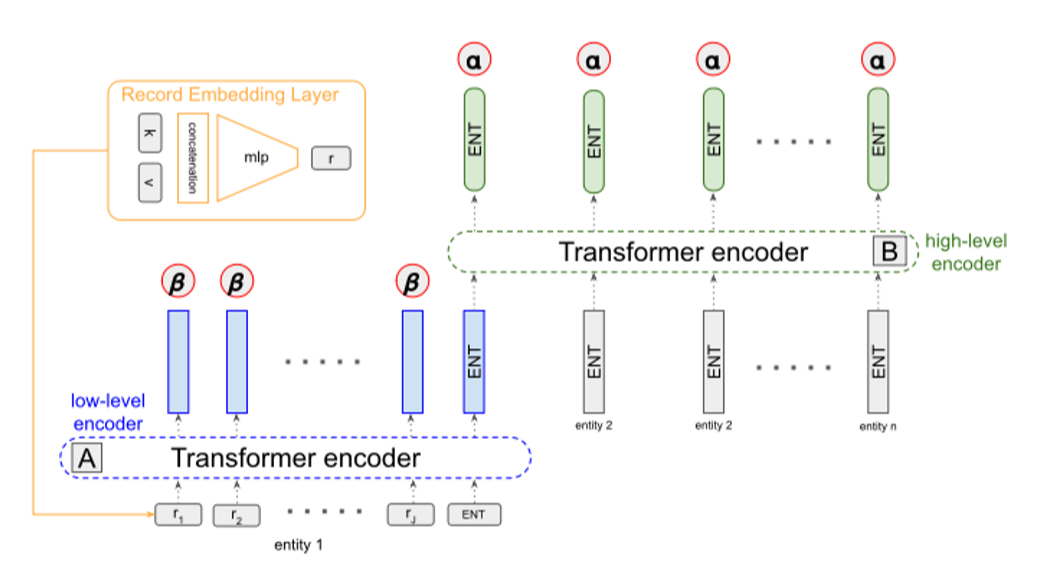
该文的主要贡献和研究是在编码器部分。作者首先将数据集处理为key-value形式的键值对记录r_(i,j),而实体e_i={r_(i,1),r_(i,2),…,r_(i,J)}则是与该实体(人名或者团队名)相关的记录的集合,总的数据结构表示为s={e_1,e_2,…,e_I},每条数据表示为(s,y),其中y表示人工撰写的参考文本。 为了获取数据的结构信息,作者引入两层Transformer分别对记录和实体进行编码,并且通过hierarchical attention机制得到编码器的上下文语境再反馈给解码器。
Low-level encoder:通过transformer比较不同记录r_(i,j)从而得到各个记录的隐藏层表示h_(i,j)。
High-level encoder:与low-level encoder相似,通过transformer比较不同底层实体表示h_i从而得到各个实体对应的隐藏层状态e_i。对所有实体得出的隐藏层状态e_i进行求平均值得到编码器最终的输出z,并用于解码器的初始化。
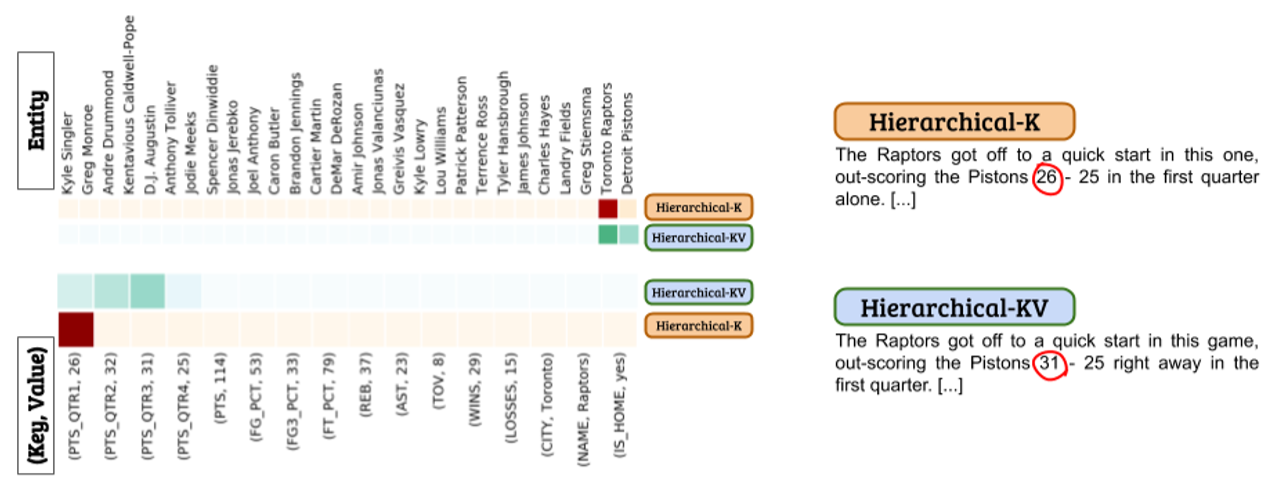
\alpha表示实体层(high)的注意力分值,\beta表示记录层(low)的注意力分值,与传统分层注意力机制不同的是,\beta如果只关注记录(key,value)中的key效果会比关注整个记录更好,value会造成噪音影响。如下图所示,同时关注key和value会使得模型无法准确地选择最恰当的数据。
- Result:
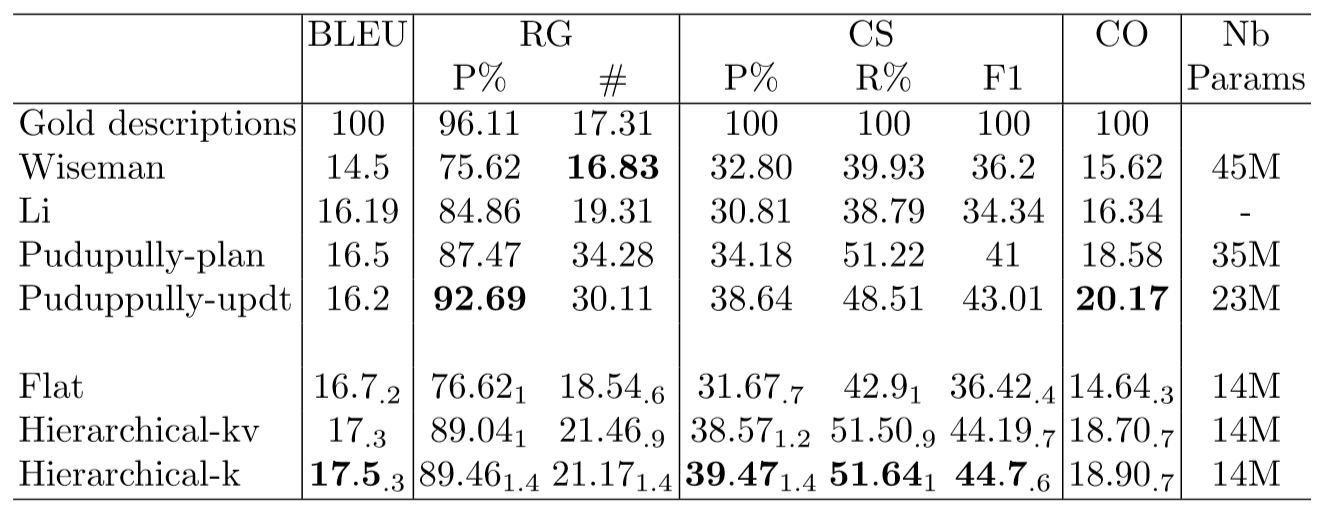
Wiseman是一种标准的带拷贝机制的编码器-解码器结构的模型。
Li是一种标准的带延迟拷贝机制的编码器-解码器结构的模型。
Puduppully-plan是先生成plan再根据其生成文本的模型。
Puduppully-updt是具有动态实体表示模块的编码器-解码器结构的模型(分层注意力机制)。
Flat是本文中编码器部分采用Transformer替换RNN的标准的编码器-解码器结构的模型。
Hierarchical-kv是本文中编码器部分采用对key和value都关注的分层Transformer的模型。
Hierarchical-k是本文中编码器部分采用只关注key的分层Transformer的模型。
通过比较Flat与Hierarchical-k/Hierarchical-kv模型,可以看出对结构化数据进行分层编码比直接顺序输入结构化数据的效果更好。 通过比较Hierarchical-k与Hierarchical-kv模型,可以看出只关注key而忽略value的效果更好,关注value可能会造成噪音效果。 通过比较Flat与Wiseman模型,可以看出Transformer应该比RNN更适合于结构化的数据。 通过比较Hierarchical-k/Hierarchical-kv与Li、Puduppully-plan模型,可以看出在编码器部分获取结构化信息比在解码器部分预测结构化信息效果更好。 通过比较Hierarchical-k与Puduppully-updt模型,可以看出Puduppully-updt在CO和RG-P%指标上更好而在其他指标上则相对较差,并且Hierarchical-k模型对数据的结构化信息只需要编码一次就可全程通用而Puduppully-updt则需要不断更新实体表示明显增加了计算的复杂度,Hierarchical-k模型显得更轻量且以更人性化的方式获得准确的流畅描述。
事实上,Hierarchical-k与Puduppully-updt有很大的相似之处,二者都在各自的模型中引入了分层注意力机制,通过先关注实体再关注实体对应的记录来获取数据的结构化信息,不同的是前者将该分层思想应用于编码器部分而后者则应用于解码器部分。另外,前者采用Transformer来替换后者所采用的RNN(LSTM)并且在分层注意力机制中选择性去除对value的关注。
PDF:https://github.com/endpaper/endpaper.github.io/blob/master/PDF/Factorization-Machines.pdf
PPT:https://github.com/endpaper/endpaper.github.io/blob/master/PPT/Factorization-Machines.pdf
PDF:https://github.com/endpaper/endpaper.github.io/blob/master/PDF/ffm.pdf ppt:https://github.com/endpaper/endpaper.github.io/blob/master/PPT/ffm.pdf