Vector codec benchmarks

We compare the vector codecs on a few datasets that hopefully are representative of real use cases.

For all cases, the procedure is the same: we instantiate the codec with an index_factory. Then we train it on 1M representative vectors. Then we evaluate:

the reconstruction error on an independent set of 1M vectors. The reconstruction is the average L2 error (non squared) after encoding and decoding back. Note that some codecs do not support reconstruction (ITQ) in a meaningful way.
the symmetric similarity search accuracy (as 1-nearest-neighbor recall at rank 1). We use 10k vectors, that we encode/decode and search the nearest neighbors in the 1M previous vectors (that are also encoded/decoded). This reflects how much the codec destroyed the discriminative ability of vectors. For binary codecs, we use the Hamming distance to evaluate this.
the asymmetric similarity search accuracy. This is the same as above, except that the queries are not encoded. This reflects a use case where query vectors that are immediately available are compared against encoded vectors from a database.

We report these measures in tables, sorted by increasing code size. We also show plots of the symmetric search accuracy. The codecs we tested were chosen from a reasonable set of baselines. It is possible that a bit more of fine-tuning can increase their performance.

These experiments have not been updated to include additive quantization options, which currently offer the best accuracy vs. memory usage tradeoffs. Please refer to the additive quantizers wiki for results on these.

SIFT1M

This is a very classical academic dataset of 1M SIFT vectors in 128D. The vectors come encoded as bytes, so it does not make sense to use more than 128 bytes to encode it.

The table below reports the most interesting operating points:

factory key	code size	codec size	recons error	sym recall @ 1	asym recall @ 1	decode time
ITQ64,LSH	8	48.7 k	-	0.051	-	-
OPQ8_48,PQ8	8	72.2 k	308.2	0.141	0.220	0.23
PCAR24,ZnLattice1x54_6	8	77.3 k	364	0.101	0.145	0.20
OPQ8_48,PQ8x10	10	216 k	301.5	0.215	0.302	0.25
OPQ8_48,PQ8x12	12	792 k	297.1	0.282	0.353	0.27
Pad128,ITQ128,LSH	16	129 k	-	0.129	-	-
OPQ16_64,PQ16	16	96.2 k	138.8	0.307	0.412	0.23
OPQ16_64,PQ16x10	20	288 k	125.9	0.428	0.504	0.28
OPQ16_64,PQ16x12	24	1.03 M	118.7	0.523	0.567	0.34
Pad256,ITQ256,LSH	32	514 k	-	0.223	-	-
PCAR64,SQ4	32	97.9 k	121.2	0.481	0.540	0.22
PCAR96,ZnLattice4x54_6	32	114 k	98.18	0.468	0.572	0.60
OPQ32_128,IVF16384,PQ32	34	8.19 M	61.86	0.612	0.666	0.14
OPQ32_128,PQ32x10	40	576 k	56.2	0.649	0.718	0.57
OPQ32_128,Residual2x14,PQ32x10	44	8.56 M	45.34	0.727	0.764	0.11
OPQ32_128,Residual2x14,PQ32x12	52	10.1 M	36.2	0.789	0.809	0.11
OPQ32_128,Residual2x14,PQ32x14	60	16.1 M	29.55	0.835	0.850	0.14
SQ4	64	1105	42.19	0.740	0.780	0.03
OPQ64_256,PQ64x10	80	1.13 M	17.32	0.878	0.896	1.04
SQ6	96	1105	9.904	0.928	0.942	0.06
OPQ64_256,PQ64x12	96	4.13 M	10.12	0.922	0.933	1.25
PCAR128,SQ8	128	131 k	3.201	0.968	0.977	0.38
SQ8	128	1105	2.468	0.976	0.979	0.04
SQfp16	256	81	0	0.992	0.992	0.03

nan means that the operation does not make sense (ITQ cannot reconstruct). The decode time is indicated as seconds to decode 1M vectors on a full machine (48 threads).

We can make the following observations:

ITQ64,LSH is a very calssical binary hash. For all operating points, it is outperformed by the product quantizer variants and even the scalar quantizer.
PQ variants give very good similarity search results. However, note that the pre-processing (OPQx) requires to store a rotation matrix in the codec, which can make it large.
for a given PQ size (eg. PQ16) increasing the number of bits per quantizer (beyond the default 8) is a good way to scale up the accuracy for a modest increase of code size
residual codecs improve a bit over the PQ, but they are a lot slower to encode, and they require even more training data
SQ8 does not give 100% accuracy as it should because of quantization artifacts.
OPQ and PCA matrices for this large datasets are bulky to store in the codec. Note that PCA matrices (but not OPQ) are stored twice, because the raw eigenvalues are kept. Hence, for a PCA with input dimension d, it is possible to subtract d*d*4 bytes from the codec size.
the lattice quantizer is better than ITQ but not as good as the scalar quantizer. This may be because the parameters were not optimized for such short vectors

Resnet50

This is a dataset of 2048-dim vectors produced by the average pooling layer of a resnet50. The vectors come from the repository low-shot-with-diffusion.

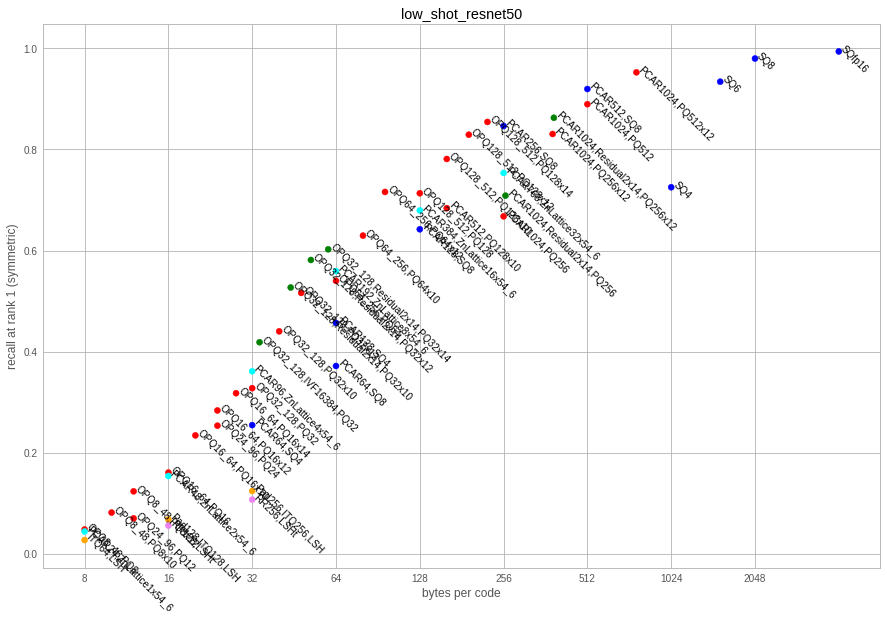
factory key	code size	codec size	recons error	sym recall @ 1	asym recall @ 1	encode time	decode time
ITQ64,LSH	8	536 k	-	0.028	-	42.41	-
OPQ8_48,PQ8	8	432 k	11.14	0.049	0.086	18.95	1.91
PCAR24,ZnLattice1x54_6	8	16.2 M	12.67	0.045	0.060	18.93	1.21
OPQ8_48,PQ8x10	10	576 k	10.89	0.082	0.129	23.43	1.95
OPQ24_96,PQ12	12	864 k	10.29	0.071	0.129	14.53	0.94
OPQ8_48,PQ8x12	12	1.13 M	10.8	0.124	0.171	40.86	0.79
Pad128,ITQ128,LSH	16	1.07 M	-	0.069	-	41.59	-
RR128,LSHt	16	1 M	-	0.056	-	18.27	-
OPQ16_64,PQ16	16	576 k	10.14	0.161	0.214	13.93	0.89
OPQ16_64,PQ16x10	20	768 k	9.904	0.235	0.278	15.74	0.86
OPQ16_64,PQ16x12	24	1.5 M	9.779	0.284	0.316	21.72	0.92
OPQ16_64,PQ16x14	28	4.5 M	9.717	0.318	0.342	45.72	0.92
Pad256,ITQ256,LSH	32	2.26 M	-	0.125	-	43.74	-
PCAR96,ZnLattice4x54_6	32	16.8 M	8.84	0.361	0.408	22.24	1.20
PCAR64,SQ4	32	16.5 M	9.96	0.255	0.291	14.65	0.84
OPQ32_128,IVF16384,PQ32	34	9.13 M	7.783	0.419	0.486	23.32	0.86
OPQ32_128,PQ32x10	40	1.5 M	7.773	0.440	0.496	29.70	1.37
OPQ32_128,Residual2x14,PQ32x10	44	9.5 M	7.571	0.527	0.569	46.01	1.00
OPQ32_128,PQ32x12	48	3 M	7.566	0.516	0.554	32.23	1.22
OPQ32_128,Residual2x14,PQ32x12	52	11 M	7.472	0.582	0.609	57.47	0.91
OPQ32_128,Residual2x14,PQ32x14	60	17 M	7.415	0.603	0.615	95.27	0.71
OPQ64_256,PQ64	64	2.25 M	5.801	0.540	0.609	17.50	1.47
PCAR128,SQ4	64	17 M	7.763	0.457	0.515	14.18	1.03
OPQ64_256,PQ64x10	80	3 M	5.367	0.630	0.691	28.46	1.87
OPQ64_256,PQ64x12	96	6 M	5.134	0.716	0.756	47.76	1.93
OPQ128_512,PQ128	128	4.5 M	4.159	0.713	0.752	19.18	4.18
PCAR128,SQ8	128	17 M	7.404	0.642	0.647	15.39	1.03
PCAR384,ZnLattice16x54_6	128	19 M	4.688	0.679	0.737	19.05	2.75
OPQ128_512,PQ128x10	160	6 M	3.769	0.781	0.811	29.75	3.30
OPQ128_512,PQ128x12	192	12 M	3.564	0.829	0.851	76.59	4.11
OPQ128_512,PQ128x14	224	36 M	3.428	0.854	0.873	309.20	9.02
PCAR256,SQ8	256	18 M	4.861	0.846	0.850	38.03	1.40
PCAR1024,Residual2x14,PQ256	260	89 M	3.6	0.709	0.769	60.21	4.64
PCAR1024,Residual2x14,PQ256x12	388	104 M	2.529	0.863	0.890	181.39	4.76
PCAR512,SQ8	512	20 M	3.233	0.919	0.921	18.14	4.00
PCAR1024,PQ512x12	768	40 M	2.01	0.953	0.955	192.48	13.30
SQ4	1024	16.1 k	3.534	0.725	0.760	50.48	0.57
SQ8	2048	16.1 k	0.2162	0.980	0.982	16.80	0.58
SQfp16	4096	81	0.004493	0.994	0.994	15.67	0.53

Observations:

ITQ is again largely outperformed
in high dimensions, the PQ codecs are easily > 100MB just to store the codec itself. The encoding time can also be prohibitive.
in high dimensions, the scalar quantizer options are interesting, especially because they do not need large codecs
the residual codecs are a bit better than the scalar ones
the lattice quantizer is competitive with OPQ variants for low bit rates (up to 32). It is much cheaper to train but a lot more expensive to code and decode.

reconstruction error plot

For comparison, here is the reconstruction error plot. The recall measures and reconstruction are heavily correlated: the lower the reconstruction error, the better the retrieval performance.

Sentence embeddings

This is a dataset with 1024-dim German sentences from the LASER toolkit.

factory key	code size	codec size	recons error	sym recall @ 1	asym recall @ 1	encode time	decode time
ITQ64,LSH	8	276 k	-	0.025	-	43.36	-
OPQ8_48,PQ8	8	240 k	0.04436	0.034	0.062	9.93	1.82
PCAR24,ZnLattice1x54_6	8	4.1 M	0.04515	0.030	0.038	9.56	1.75
OPQ8_48,PQ8x10	10	384 k	0.04405	0.052	0.080	13.59	0.47
OPQ24_96,PQ12	12	480 k	0.04337	0.054	0.101	7.58	0.63
OPQ8_48,PQ8x12	12	960 k	0.04384	0.070	0.090	33.32	0.47
Pad128,ITQ128,LSH	16	580 k	-	0.063	-	32.96	-
OPQ16_64,PQ16	16	320 k	0.04318	0.098	0.127	13.10	0.52
OPQ16_64,PQ16x10	20	512 k	0.04292	0.126	0.143	10.93	0.65
OPQ16_64,PQ16x12	24	1.25 M	0.04278	0.141	0.157	15.56	0.66
OPQ24_96,PQ24	24	480 k	0.04203	0.155	0.202	40.63	0.59
OPQ16_64,PQ16x14	28	4.25 M	0.0427	0.151	0.160	102.27	0.59
Pad256,ITQ256,LSH	32	1.25 M	-	0.121	-	33.70	-
OPQ32_128,PQ32	32	640 k	0.04111	0.206	0.255	18.77	0.83
PCAR64,SQ4	32	4.26 M	0.04323	0.090	0.116	16.19	0.51
PCAR96,ZnLattice4x54_6	32	4.38 M	0.04168	0.201	0.222	8.69	0.81
OPQ32_128,IVF16384,PQ32	34	8.63 M	0.04079	0.242	0.275	82.16	0.42
OPQ32_128,PQ32x10	40	1 M	0.04071	0.258	0.288	22.44	0.79
OPQ32_128,Residual2x14,PQ32x10	44	9 M	0.04055	0.289	0.305	34.87	0.41
OPQ32_128,PQ32x12	48	2.5 M	0.04052	0.292	0.307	91.29	0.89
OPQ32_128,Residual2x14,PQ32x14	60	16.5 M	0.04038	0.315	0.322	94.09	0.41
OPQ64_256,PQ64	64	1.25 M	0.03845	0.363	0.421	12.66	1.44
PCAR128,SQ4	64	4.51 M	0.04125	0.189	0.230	13.19	0.71
PCAR64,SQ8	64	4.26 M	0.0426	0.166	0.165	17.95	0.54
OPQ64_256,PQ64x10	80	2 M	0.03791	0.435	0.469	111.14	1.75
OPQ64_256,PQ64x12	96	5 M	0.03767	0.473	0.498	213.54	1.64
OPQ128_512,PQ128	128	2.5 M	0.0355	0.534	0.599	16.70	3.06
PCAR384,ZnLattice16x54_6	128	5.51 M	0.03623	0.554	0.596	10.71	1.80
OPQ128_512,PQ128x10	160	4 M	0.03497	0.630	0.668	25.14	3.18
OPQ128_512,PQ128x12	192	10 M	0.03467	0.680	0.713	68.92	3.09
OPQ128_512,PQ128x14	224	34 M	0.03452	0.711	0.729	338.22	7.07
PCAR1024,PQ256	256	9.01 M	0.01069	0.646	0.700	122.88	7.62
PCAR256,SQ8	256	5.01 M	0.03747	0.528	0.528	10.69	1.08
PCAR768,ZnLattice32x54_6	256	7.01 M	0.03314	0.724	0.780	12.76	3.42
PCAR1024,Residual2x14,PQ256x12	388	88 M	0.004612	0.839	0.867	208.75	3.67
PCAR1024,PQ512	512	9.01 M	0.003313	0.881	0.901	33.06	8.53
PCAR512,SQ8	512	6.01 M	0.03431	0.768	0.768	11.32	2.00
PCAR1024,PQ512x12	768	24 M	0.001003	0.965	0.970	227.62	13.56
SQ6	768	8273	0.003924	0.843	0.872	22.25	0.47
SQ8	1024	8273	0.0009623	0.955	0.965	18.18	0.27
SQfp16	2048	81	1.041e-05	0.999	0.999	37.52	0.28

Observations:

Although the dataset is lower-dimensional than the resnet50 embeddings, the raw retrieval performance is lower, so it is also more difficult to index.
Encoding times can be quite prohibitive for residual codecs.
the lattice quantizer is very competitive in this setting. It obtains competitive accuracies with the PQ variants.

The evaluation code is in bench_standalone_codec.py with driver script run_on_cluster.bash.

The plots were produced with this notebook