【Hackathon 6th No.39】XPINN 迁移至 PaddleScience (PaddlePaddle#849)

* add XPINNs example * comment * add conf file * refine code * fix comment * fix data type * fix data type * Update examples/xpinn/plotting.py * Update examples/xpinn/conf/xpinn.yaml * refine code * refine doc * refine doc * fix doc * fix bugs --------- Co-authored-by: HydrogenSulfate <490868991@qq.com>
huohuohuohuohuo123 · May 30, 2024 · ce050a3 · ce050a3
1 parent 452ba2f
commit ce050a3
Show file tree

Hide file tree

Showing 5 changed files with 1,151 additions and 0 deletions.
diff --git a/docs/zh/examples/xpinns.md b/docs/zh/examples/xpinns.md
@@ -0,0 +1,184 @@
+# Extended Physics-Informed Neural Networks (XPINNs)
+
+=== "模型训练命令"
+
+    ``` sh
+    # linux
+    wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/XPINN/XPINN_2D_PoissonEqn.mat -P ./data/
+
+    # windows
+    # curl https://paddle-org.bj.bcebos.com/paddlescience/datasets/XPINN/XPINN_2D_PoissonEqn.mat --output ./data/XPINN_2D_PoissonEqn.mat
+
+    python xpinn.py
+
+    ```
+
+## 1. 背景简介
+
+求解偏微分方程（PDE）是一类基础的物理问题，随着人工智能技术的高速发展，利用深度学习求解偏微分方程成为新的研究趋势。[XPINNs（Extended Physics-Informed Neural Networks）](https://doi.org/10.4208/cicp.OA-2020-0164)是一种适用于物理信息神经网络（PINNs）的广义时空域分解方法，以求解任意复杂几何域上的非线性偏微分方程。
+
+XPINNs 通过广义时空区域分解，有效地提高了模型的并行能力，并且支持高度不规则的、凸/非凸的时空域分解，界面条件是简单的。XPINNs 可扩展到任意类型的偏微分方程，而不论方程是何种物理性质。
+
+精确求解高维复杂的方程已经成为科学计算的最大挑战之一，XPINNs 的优点使其成为模拟复杂方程的适用方法。
+
+## 2. 问题定义
+
+二维泊松方程：
+
+$$ \Delta u = f(x, y),  x,y \in \Omega \subset R^2$$
+
+## 3. 问题求解
+
+接下来开始讲解如何将问题一步一步地转化为 PaddleScience 代码，用深度学习的方法求解该问题。
+为了快速理解 PaddleScience，接下来仅对模型构建、方程构建、计算域构建等关键步骤进行阐述，而其余细节请参考 [API文档](../api/arch.md)。
+
+### 3.1 数据集下载
+
+如下图所示，数据集包含计算域的三个子区域的数据：红色区域的边界和残差点；黄色区域的界面；以及绿色区域的界面。
+
+<figure markdown>
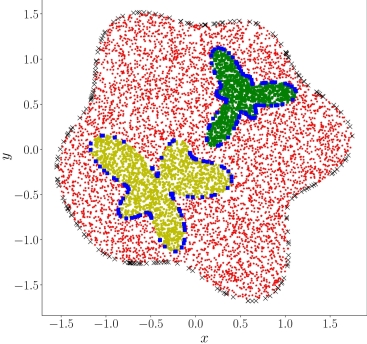+  ![](https://ai-studio-static-online.cdn.bcebos.com/27ef9bddb0604ef58007f9be6a3364ac0336f476ac894233a6f6b1c97ab68c5c)
+  <figcaption>二维泊松方程的三个子区域</figcaption>
+</figure>
+
+计算域的边界表达式如下。
+
+$$ \gamma =1.5+0.14 sin(4θ)+0.12 cos(6θ)+0.09 cos(5θ), θ \in [0,2π) $$
+
+红色区域和黄色区域的界面的表达式如下。
+
+$$ \gamma_1 =0.5+0.18 sin(3θ)+0.08 cos(2θ)+0.2 cos(5θ), θ \in [0,2π)$$
+
+$$ \gamma_2 =0.34+0.04 sin(5θ)+0.18 cos(3θ)+0.1 cos(6θ), θ \in [0,2π) $$
+
+执行以下命令，下载并解压数据集。
+
+``` sh
+wget -nc https://paddle-org.bj.bcebos.com/paddlescience/datasets/XPINN/XPINN_2D_PoissonEqn.mat -P ./data/
+```
+
+### 3.3 模型构建
+
+在本问题中，我们使用神经网络 `MLP` 作为模型，在模型代码中定义三个 `MLP` ，分别作为三个子区域的模型。
+
+``` py linenums="301"
+--8<--
+examples/xpinn/xpinn.py:301:302
+--8<--
+```
+
+模型训练时，我们将使用 XPINN 方法分别计算每个子区域的模型损失。
+
+<figure markdown>
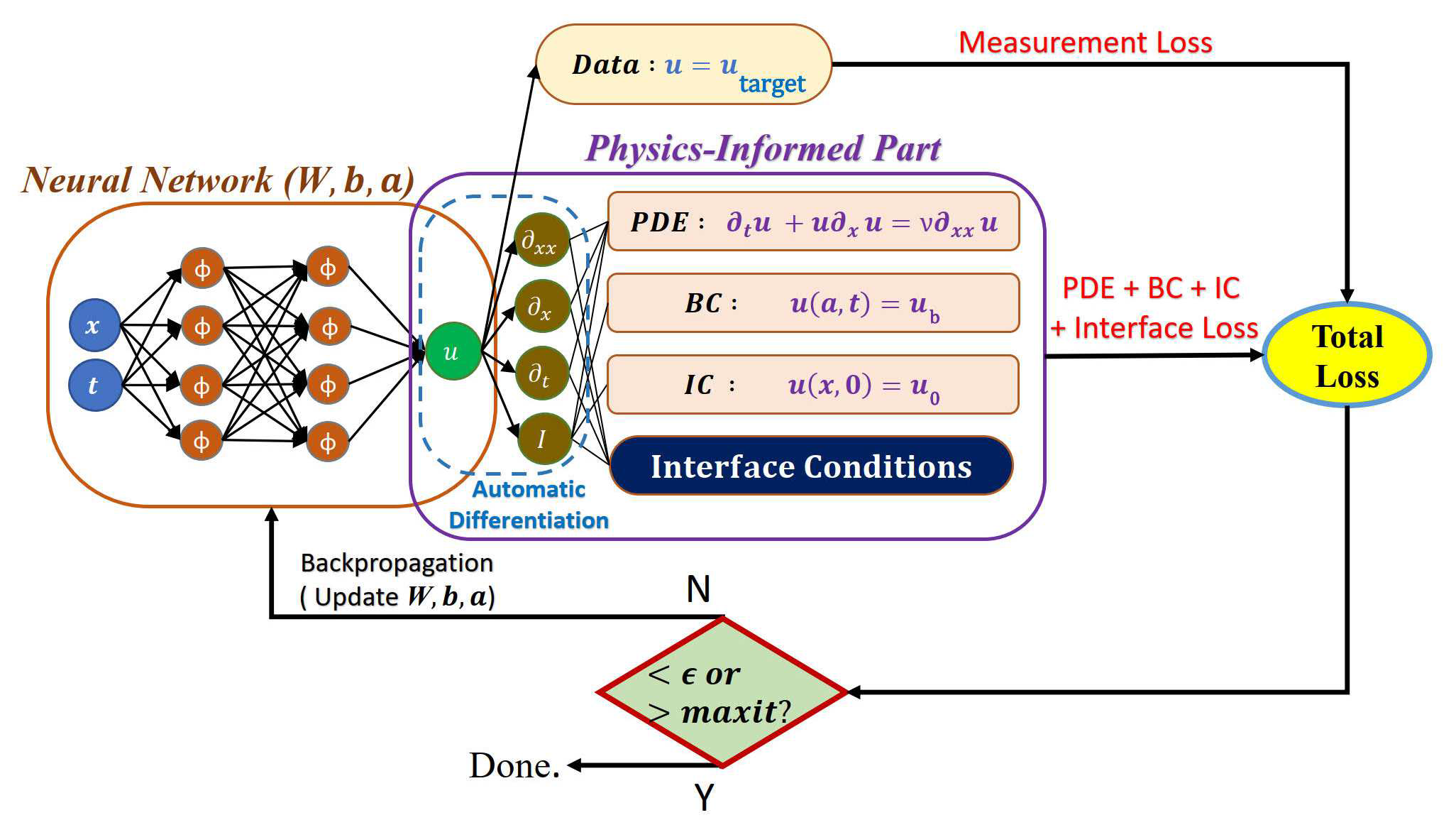+  ![](https://ai-studio-static-online.cdn.bcebos.com/d30ac172809343c5ac9d2b44d3657efd8e30949fd8f44174bf6221e14c31f6bf)
+  <figcaption>XPINN子网络的训练过程</figcaption>
+</figure>
+
+### 3.4 约束构建
+
+在本案例中，我们使用监督数据集对模型进行训练，因此需要构建监督约束。
+
+在定义约束之前，我们需要指定数据集的路径等相关配置，将这些信息存放到对应的 YAML 文件中，如下所示。
+
+``` yaml linenums="43"
+--8<--
+examples/xpinn/conf/xpinn.yaml:43:44
+--8<--
+```
+
+接着定义训练损失函数的计算过程，调用 XPINN 方法计算损失，如下所示。
+
+``` py linenums="130"
+--8<--
+examples/xpinn/xpinn.py:130:191
+--8<--
+```
+
+最后构建监督约束，如下所示。
+
+``` py linenums="304"
+--8<--
+examples/xpinn/xpinn.py:304:311
+--8<--
+```
+
+### 3.5 超参数设定
+
+设置训练轮数等参数，如下所示。
+
+``` yaml linenums="83"
+--8<--
+examples/xpinn/conf/xpinn.yaml:83:88
+--8<--
+```
+
+### 3.6 优化器构建
+
+训练过程会调用优化器来更新模型参数，此处选择较为常用的 `Adam` 优化器。
+
+``` py linenums="337"
+--8<--
+examples/xpinn/xpinn.py:337:338
+--8<--
+```
+
+### 3.7 评估器构建
+
+在训练过程中通常会按一定轮数间隔，用验证集(测试集)评估当前模型的训练情况，因此使用 `ppsci.validate.SupervisedValidator` 构建评估器。
+
+``` py linenums="324"
+--8<--
+examples/xpinn/xpinn.py:324:335
+--8<--
+```
+
+评估指标为预测结果和真实结果的 RMSE 值，这里需自定义指标计算函数，如下所示。
+
+``` py linenums="194"
+--8<--
+examples/xpinn/xpinn.py:194:219
+--8<--
+```
+
+### 3.8 模型训练
+
+完成上述设置之后，只需要将上述实例化的对象按顺序传递给 `ppsci.solver.Solver`，然后启动训练。
+
+``` py linenums="340"
+--8<--
+examples/xpinn/xpinn.py:340:357
+--8<--
+```
+
+### 3.9 结果可视化
+
+训练完毕之后程序会对测试集中的数据进行预测，并以图片的形式对结果进行可视化，如下所示。
+
+``` py linenums="360"
+--8<--
+examples/xpinn/xpinn.py:360:384
+--8<--
+```
+
+## 4. 完整代码
+
+``` py linenums="1" title="cfdgcn.py"
+--8<--
+examples/xpinn/xpinn.py
+--8<--
+```
+
+## 5. 结果展示
+
+下方展示了对计算域中每个点的预测值结果、参考结果和相对误差。
+
+<figure markdown>
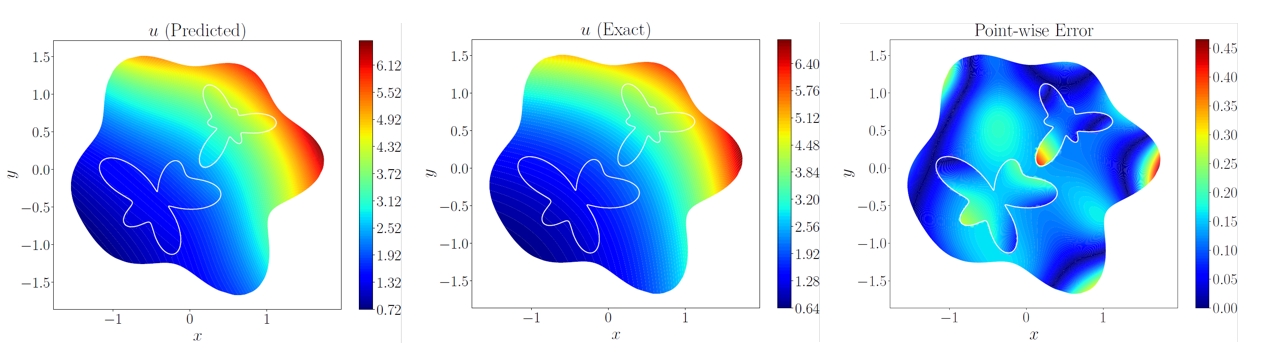+  ![](https://ai-studio-static-online.cdn.bcebos.com/3f3b0dda860041009c7f87aae099871d85dc9694bd924608afa0af2c6101d37e)
+  <figcaption>预测结果和参考结果的对比</figcaption>
+</figure>
+
+可以看到模型预测结果与真实结果相近，若增大训练轮数，模型精度会进一步提高。
+
+## 6. 参考文献
+
+* [A.D.Jagtap, G.E.Karniadakis, Extended Physics-Informed Neural Networks (XPINNs): A Generalized Space-Time Domain Decomposition Based Deep Learning Framework for Nonlinear Partial Differential Equations, Commun. Comput. Phys., Vol.28, No.5, 2002-2041, 2020.](https://doi.org/10.4208/cicp.OA-2020-0164)
diff --git a/examples/xpinn/conf/xpinn.yaml b/examples/xpinn/conf/xpinn.yaml
@@ -0,0 +1,122 @@
+hydra:
+  run:
+    # dynamic output directory according to running time and override name
+    dir: outputs_xpinn/${now:%Y-%m-%d}/${now:%H-%M-%S}/${hydra.job.override_dirname}
+  job:
+    name: ${mode} # name of logfile
+    chdir: false # keep current working direcotry unchaned
+    config:
+      override_dirname:
+        exclude_keys:
+          - TRAIN.checkpoint_path
+          - TRAIN.pretrained_model_path
+          - EVAL.pretrained_model_path
+          - mode
+          - output_dir
+          - log_freq
+  callbacks:
+    init_callback:
+      _target_: ppsci.utils.callbacks.InitCallback
+  sweep:
+    # output directory for multirun
+    dir: ${hydra.run.dir}
+    subdir: ./
+
+# general settings
+mode: train # running mode: train/eval
+seed: 134
+output_dir: ${hydra:run.dir}
+log_freq: 20
+
+# model settings
+MODEL:
+  num_boundary_points: 200 # Boundary points from subdomain 1
+  num_residual1_points: 5000 # Residual points in three subdomain 1
+  num_residual2_points: 1800 # Residual points in three subdomain 2
+  num_residual3_points: 1200 # Residual points in three subdomain 3
+  num_interface1: 100 # Interface points along the two interfaces
+  num_interface2: 100
+  layers1: [2, 30, 30, 1]
+  layers2: [2, 20, 20, 20, 20, 1]
+  layers3: [2, 25, 25, 25, 1]
+
+# set training data file
+DATA_FILE: "./data/XPINN_2D_PoissonEqn.mat"
+
+# training settings
+TRAIN:
+  input_keys:
+    [
+      "residual1_x",
+      "residual1_y",
+      "residual2_x",
+      "residual2_y",
+      "residual3_x",
+      "residual3_y",
+      "interface1_x",
+      "interface1_y",
+      "interface2_x",
+      "interface2_y",
+      "boundary_x",
+      "boundary_y",
+    ]
+  label_keys: ["boundary_u_exact"]
+  alias_dict:
+    {
+      "residual1_x": "x_f1",
+      "residual1_y": "y_f1",
+      "residual2_x": "x_f2",
+      "residual2_y": "y_f2",
+      "residual3_x": "x_f3",
+      "residual3_y": "y_f3",
+      "interface1_x": "xi1",
+      "interface1_y": "yi1",
+      "interface2_x": "xi2",
+      "interface2_y": "yi2",
+      "boundary_x": "xb",
+      "boundary_y": "yb",
+      "boundary_u_exact": "ub",
+      "residual_u_exact": "u_exact",
+      "residual2_u_exact": "u_exact2",
+      "residual3_u_exact": "u_exact3",
+    }
+  epochs: 501
+  iters_per_epoch: 1
+  save_freq: 50
+  eval_during_train: true
+  eval_freq: 50
+  learning_rate: 0.0008
+  pretrained_model_path: null
+  checkpoint_path: null
+
+# evaluation settings
+EVAL:
+  label_keys:
+    [
+      "boundary_u_exact",
+      "residual_u_exact",
+      "residual2_u_exact",
+      "residual3_u_exact",
+    ]
+  alias_dict:
+    {
+      "residual1_x": "x_f1",
+      "residual1_y": "y_f1",
+      "residual2_x": "x_f2",
+      "residual2_y": "y_f2",
+      "residual3_x": "x_f3",
+      "residual3_y": "y_f3",
+      "interface1_x": "xi1",
+      "interface1_y": "yi1",
+      "interface2_x": "xi2",
+      "interface2_y": "yi2",
+      "boundary_x": "xb",
+      "boundary_y": "yb",
+      "boundary_u_exact": "ub",
+      "residual_u_exact": "u_exact",
+      "residual2_u_exact": "u_exact2",
+      "residual3_u_exact": "u_exact3",
+    }
+  batch_size: 1
+  pretrained_model_path: null
+  eval_with_no_grad: false