Mandelbrot Kata

This a little programming exercise using the fractal domain, in particular the Mandelbrot Set.

Detailed explanations about the Mandelbrot Set can be found here: https://en.wikipedia.org/wiki/Mandelbrot_set

The goals of the kata are:

• Understand a little bit the mathematical concepts behind fractals.
• Apply Test-First Programming approach.
• Improve OO programming skills.

In order to finish the kata you have to draw two versions of the Mandelbrot fractal:

• ASCII graph: see file mandelbrot-160x160.txt
• Image (background white and mandelbrot set in black): see file mandelbrot-160x160.png

Math

Basically, there is a mathematical formula for complex number:

f(x) = z² + c

where z and c are complex number.

The Mandelbrot set is the set of complex numbers c for which the function does not diverge when iterated from z=0. Than means, given a c complex number, if you apply the formula to that number n times using the previous result as the new z number, that c belongs to Mandelbrot Set if the sequence does not diverge.

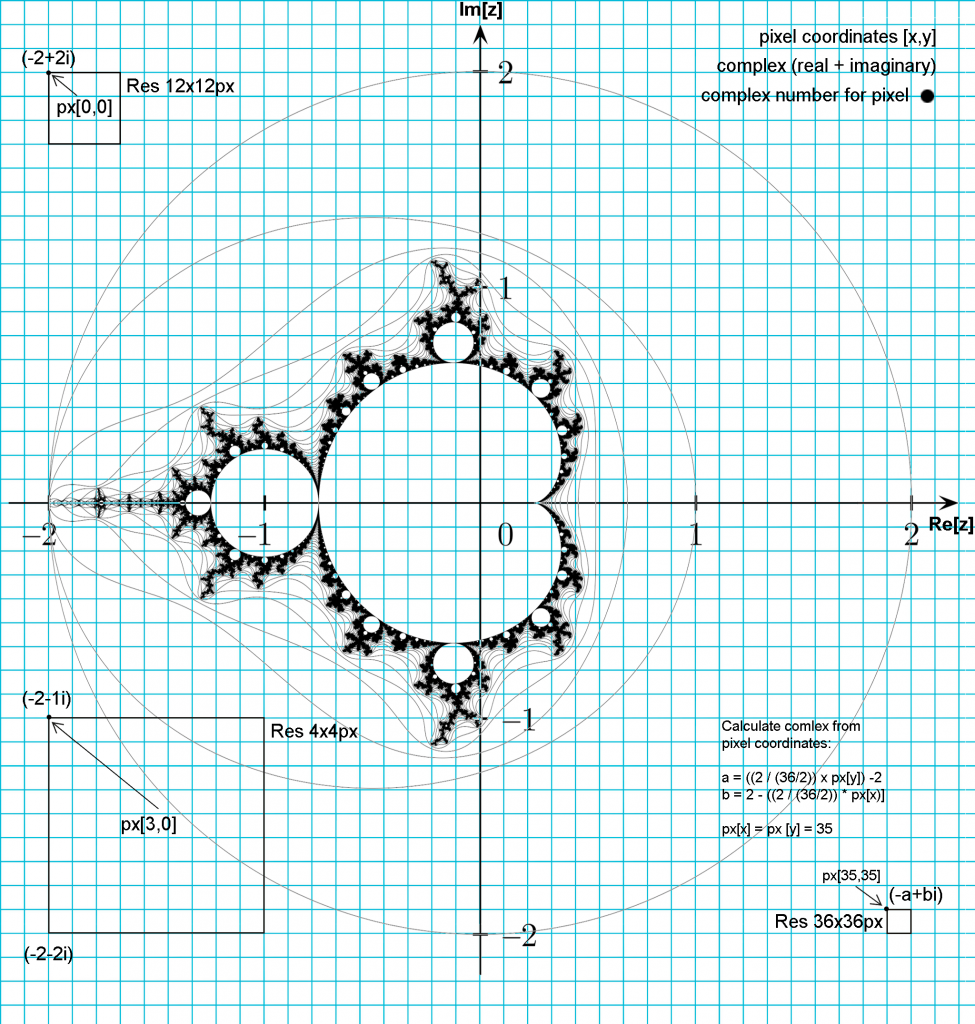
You can represent those complex number in a graph where x-axis is the real part of the complex number and y-axis is the imaginary part.

Drawing the fractal

You have to draw the portion of the graph between -2 and 2 real and imaginary parts. Mandelbrot Set is inside those limits.

Prerequisites

PHP

PHP 7.4

Installation

PHP without docker

composer install

PHP with docker

docker build -t php-mandelbrot .
docker run -it --rm \
	-v "$PWD":/usr/src/app \
	-w /usr/src/app \
	-u $(id -u ${USER}):$(id -g ${USER}) \
	php-mandelbrot \
    composer install

Running the tests

PHP without docker

./vendor/bin/phpunit

PHP with docker

docker run -it --rm \
	-v "$PWD":/usr/src/app \
	-w /usr/src/app \
	-u $(id -u ${USER}):$(id -g ${USER}) \
	php-mandelbrot

Execute only one test class

docker run -it --rm \
	-v "$PWD":/usr/src/app \
	-w /usr/src/app \
	-u $(id -u ${USER}):$(id -g ${USER}) \
	php-mandelbrot \
    ./vendor/bin/phpunit --filter 'MandelbrotFormulaShould'

Acknowledgments

• This kata was inspired by: https://github.com/edyoung/gnofract4d

Similar projects

• https://github.com/ziqbal/mandelbrot

Performance

It's very bad. It's not the goal of the project.

For 8192px image:

• Size: 8192x8192px
• Iter: 200
• Decimal precision: 28
• Time: 179m (2,98h)
• Performance: 0,17ms/px
• Min number step: 0,00048828125 (4/8192)

For 16384px image:

• Size: 16384x16384px
• Iter: 200
• Decimal precision: 28
• Time: 673m (11,21h)
• Performance: 0,17ms/px
• Min number step: 0,000244140625 (4/16384)

TODO

Increase performance:

• Use PHP parallel
• Symmetry real axis.
• Mapping from pixel to complex number only for one image corner. Calculate next pixel complex from previous complex number.

More fun:

• Auto zoom.
• Build only the image for a tile.
• Add color map (grey scale).
• Add JS GUI like this: https://github.com/cslarsen/mandelbrot-js

Arbitrary precision:

• Test it with numbers greater than PHP float precision.