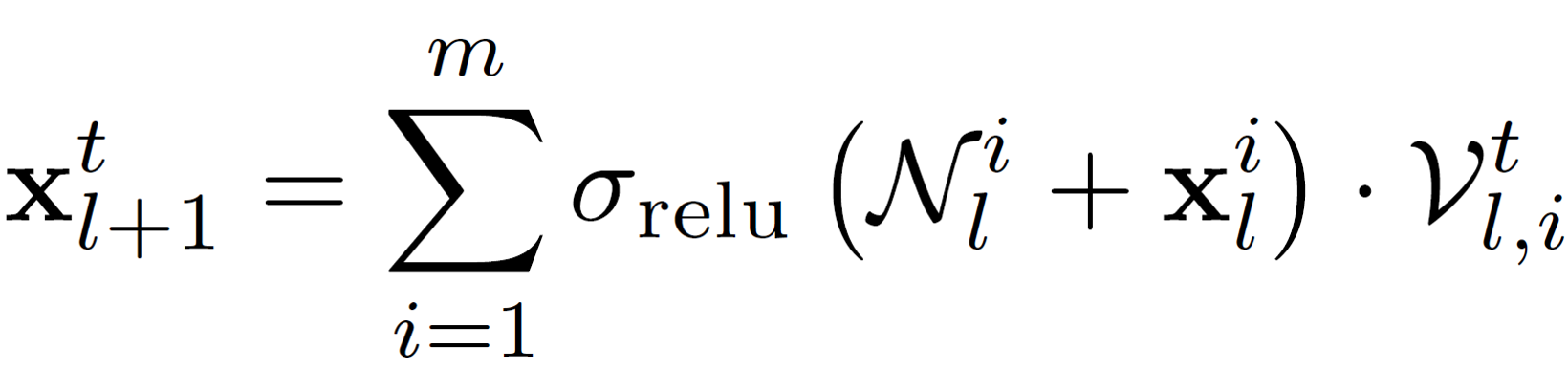Annoucement: This repo is outdated. Please refer to the new PNN repo here: https://github.com/juefeix/pnn.pytorch.update
The demo code in our original PNN repo was meant to showcase a working PNN module in a minimalist way, with much shortened training cycle. Unfortunately, the default smoothing flag in computing test accuracy was erroneous, as I have acknowledged in my initial Reddit reply. This default flag resulted in higher-than-actual accuracy, and mislead me to pick a variant of PNN with 7x7 filters in the first layer instead of 3x3 filters (which improves performance), for our public repo.
There is an easy fix to improve the model posted in our original PNN repo. We just need to change 4 lines of code and it should reach the same performance level as in the updated PNN repo. Here is what you need to do.
-
(1) Change the default smoothing flag to
Falsein/plugins/monitor.py, see here. The line should be changed todef __init__(self, smoothing=False, smoothness=0.7):. -
(2) Resetting LR scheduling in
train.pyfor longer training cycles, see here. The line should be changed toreturn self.lr * ((0.2 ** int(epoch >= 150)) * (0.2 ** int(epoch >= 250)) * (0.2 ** int(epoch >= 300)) * (0.2 ** int(epoch >= 350)) * (0.2 ** int(epoch >= 400))). -
(3-4) Using 3x3 conv for the first PNN layer in
/models/naiveresnet.py, see here. The line should be changed tonn.Conv2d(nchannels,nfilters,kernel_size=3,stride=1,padding=1,bias=False),. Next, comment out Line 95. Finally, add a linepool = 4after Line 96 for setting the proper average pool kernel size.
The original code portion will be kept untouched for exhibition purpose for now.
PyTorch implementation of CVPR'18 - Perturbative Neural Networks http://xujuefei.com/pnn.html
https://arxiv.org/pdf/1806.01817v1.pdf
Marios Savvides
Carnegie Mellon University and Michigan State University
Understanding Perturbative Neural Networks (PNN)
Convolutional neural networks are witnessing wide adoption in computer vision systems with numerous applications across a range of visual recognition tasks. Much of this progress is fueled through advances in convolutional neural network architectures and learning algorithms even as the basic premise of a convolutional layer has remained unchanged. In this paper, we seek to revisit the convolutional layer that has been the workhorse of state-of-the-art visual recognition models. We introduce a very simple, yet effective, module called a perturbation layer as an alternative to a convolutional layer. The perturbation layer does away with convolution in the traditional sense and instead computes its response as a weighted linear combination of non-linearly activated additive noise perturbed inputs. We demonstrate both analytically and empirically that this perturbation layer can be an effective replacement for a standard convolutional layer. Empirically, deep neural networks with perturbation layers, called Perturbative Neural Networks (PNNs), in lieu of convolutional layers perform comparably with standard CNNs on a range of visual datasets (MNIST, CIFAR-10, PASCAL VOC, and ImageNet) with fewer parameters.
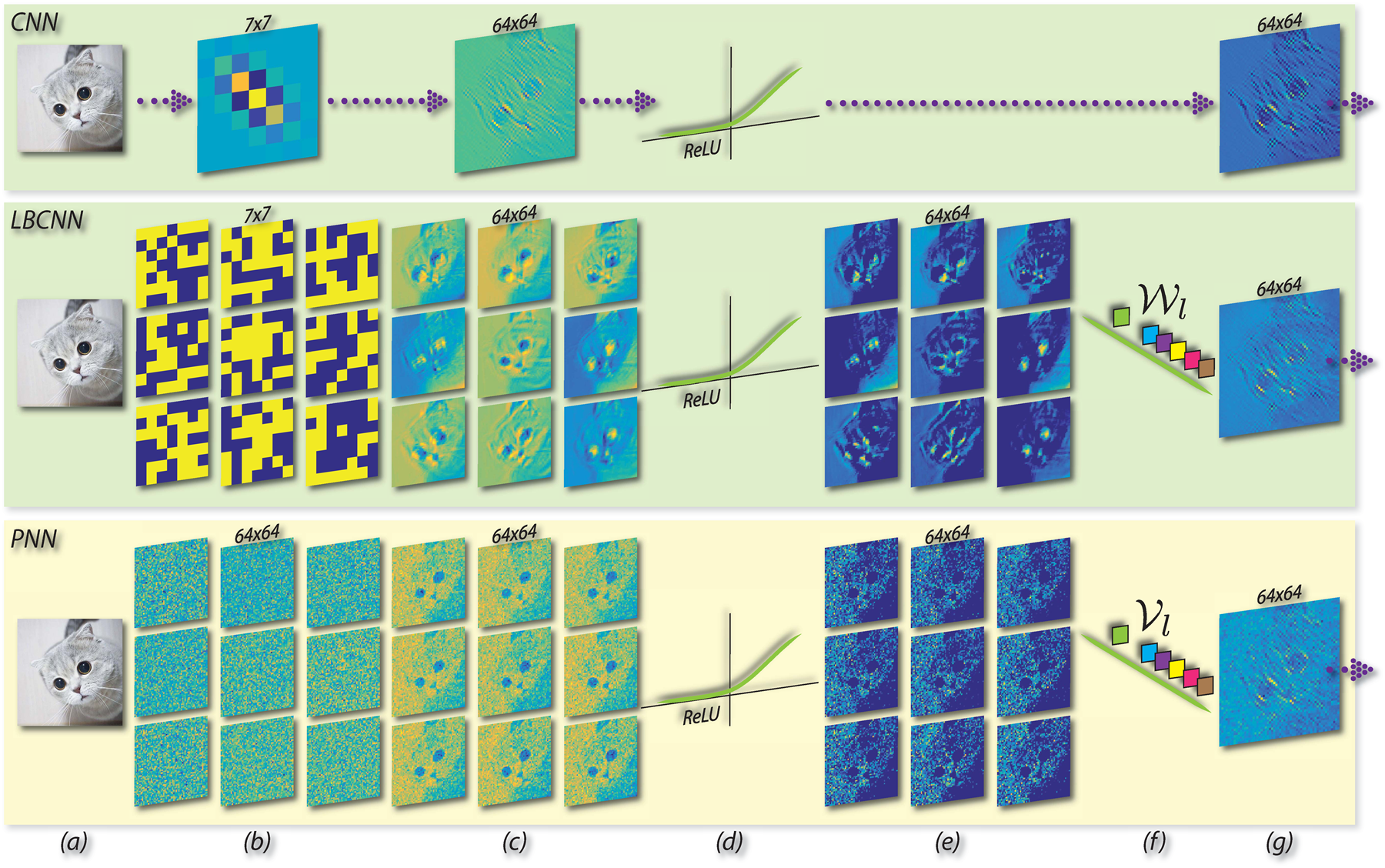
In Local Binary Convolutional Neural Networks (LBCNN), CVPR'17, convolving with a binary filter is equivalent to addition and subtraction among neighbors within the patch. Similarly, convolving with a real-valued filter is equivalent to the linear combination of the neighbors using filter weights. Either way, the convolution is a linear function that transforms the center pixel x5 to a single pixel in the output feature map, by involving its neighbors. Can we arrive at a simpler mapping function?
Basic modules in CNN, LBCNN, and PNN. Wl and Vl are the learnable weights for local binary convolution layer and the proposed perturbation layer respectively. For PNN: (a) input, (b) fixed non-learnable perturbation masks, (c) response maps by addition with perturbation masks, (d) ReLU, (e) activated response maps, (f) learnable linear weights for combining the activated response maps, (g) feature map.
N^i is the i-th random additive perturbation mask. The linear weights V are the only learnable parameters of a perturbation layer.
Perturbation residual module.
-
Novel deep learning model in lieu of convolutional layers
-
Theoretical analysis on relating PNN and CNN
-
A macro view: we have shown that PNN layer can be a good approximation for any CNN layer.
-
A micro view: we have shown that convolution operation behaves like additive noise under mild assumptions.
-
-
On-par performance with standard CNNs (ImageNet, CIFAR-10, MNIST, and Pascal VOC)
- Felix Juefei-Xu, Vishnu Naresh Boddeti, and Marios Savvides, Perturbative Neural Networks,
- To appear in IEEE Computer Vision and Pattern Recognition (CVPR), 2018.
@inproceedings{juefei-xu2018pnn,
title={{Perturbative Neural Networks}},
author={Felix Juefei-Xu and Vishnu Naresh Boddeti and Marios Savvides},
booktitle={IEEE Computer Vision and Pattern Recognition (CVPR)},
month={June},
year={2018}
}
The code base is built upon PyTorchNet.
PyTorch 0.4.0
CIFAR-10
PNN (~92-93% after 80 epochs, no test-time image flipping)
python main.py --net-type 'noiseresnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 10 --learning-rate 1e-4