This repo houses the new PNN code, along with our responses to the issue raised in the recent Reddit discussion. The code is based on Michael Klachko’s repo with slight modification in model.py and main.py. All changes are marked.
TL;DR (1) alleged performance drop (~5%) is primarily due to various inconsistencies in Michael Klachko’s implementation of PNN and suboptimal choices of hyper-parameters. (2) the practical effectiveness of PNN method stands.
Recent Reddit Discussion: I tried to reproduce results from a CVPR18 paper, here's what I found
Michael Klachko's re-implementation and his findings
The original PNN Repository (will be kept untouched)
Based on our analysis, the alleged performance drop (~5%) is primarily due to various inconsistencies in Michael Klachko’s implementation of PNN and suboptimal choices of hyper-parameters.
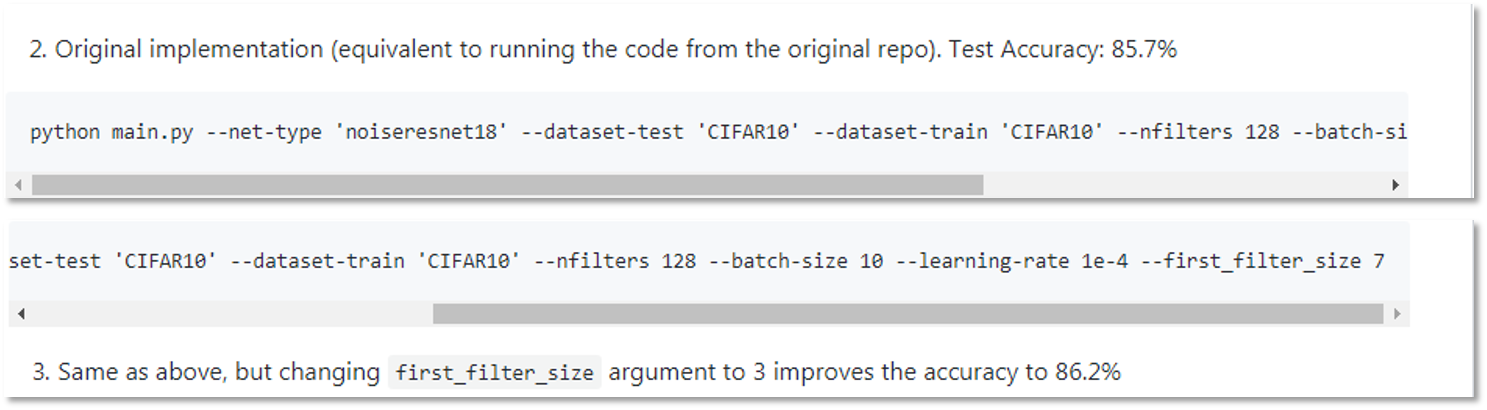
With the sub-optimal PNN implementation and hyper-parameters, MK's implementation gets ~85-86% on CIFAR-10, and a 5% drop in performance is observed as shown in the following snapshot from his repo.
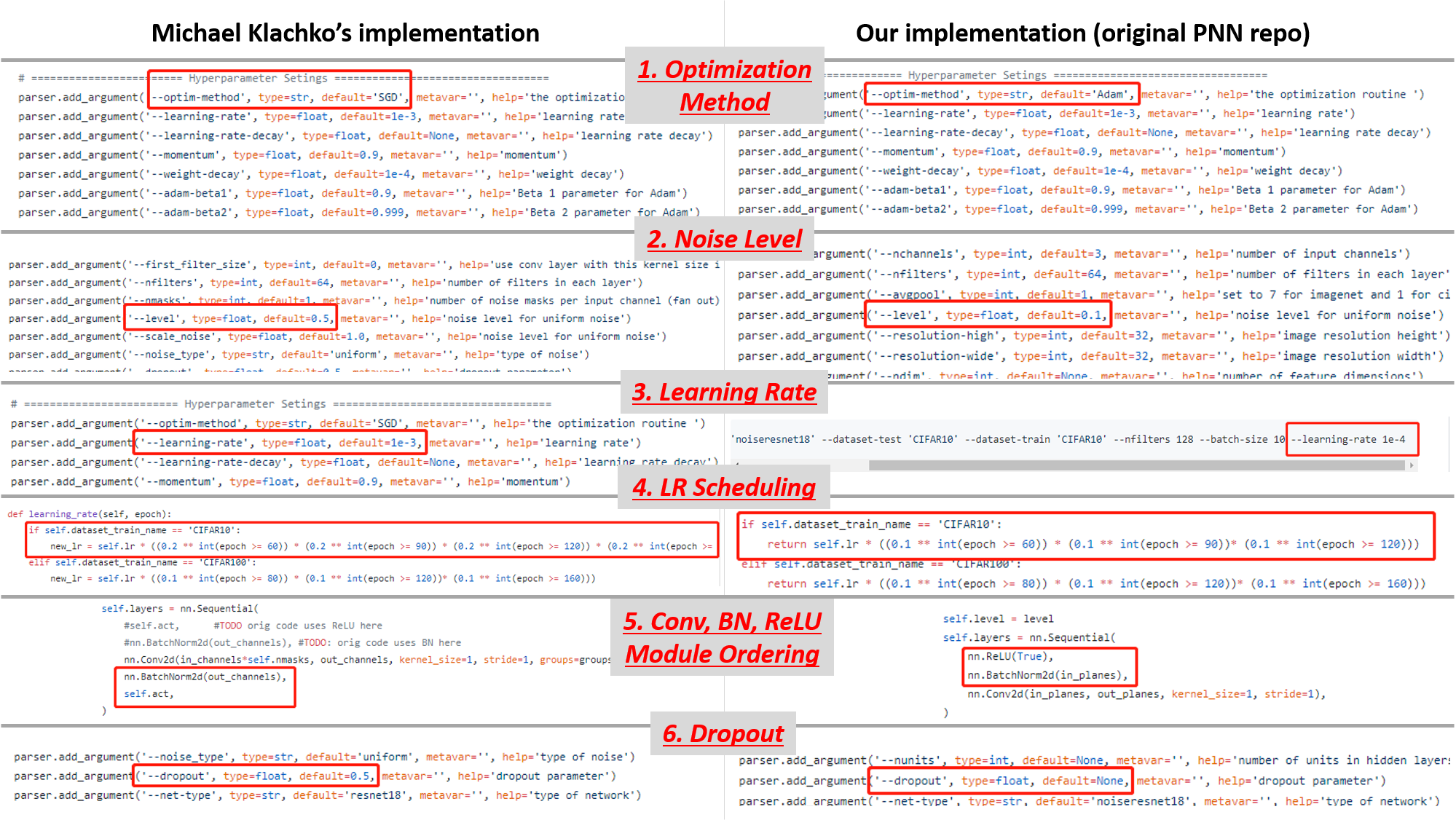
Comparing MK's implementation with ours, we are able to spot the following inconsistencies:
- The optimization method is different: MK uses SGD, ours uses Adam.
- The additive noise level is different: MK uses 0.5, ours uses 0.1.
- The learning rate is different: MK uses 1e-3, ours uses 1e-4.
- The learning rate scheduling is different: MK uses this, ours uses this.
- The Conv-BN-ReLU module ordering is different: MK uses this, ours uses this.
- The dropout use is different: MK uses 0.5, ours uses None.
The visual summary of the various inconsistencies are shown in the following figure. MK's implementation is on the left hand side, and ours is on the right hand side.
Among these inconsistencies, based on our limited number of trials, the first two (optimization method and noise level) have the most negative impact on the PNN performance. The choice of optimization method is indeed very important and on smaller scale experiments, each optimization method (SGD, Adam, RMSProp, etc.) will traverse the optimization landscape quite differently. The choice of additive noise level is also very important, and we will come back to that in Section 3.
So, let's see how PNN performs after setting the correct hyper-parameters. Keeping the same number of noise masks (--nfilters 128), we are able to reach 90.35%, as opposed to MK's ~85-86% accuracy reported in his repo.
python main.py --net-type 'noiseresnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 128 --batch-size 10 --learning-rate 1e-4 --first_filter_size 3 --level 0.1 --optim-method Adam --nepochs 450
As of now, most of the re-evaluation of the CVPR experiments are done. There is a very small portion of the experiments that are affected by the erroneous default flag in the smoothing function. For those affected, there is a small drop in performance and can be compensated for by increasing the network parameters (e.g. # of noise masks). We will update the results in the arxiv version of the PNN paper.
The content below this line was not covered in the original CVPR paper.
The content to be discussed next was not originally covered in our CVPR paper and was meant to be further explored and discussed in subsequent follow-up work of PNN. One of the topics is applying perturbative noise at all layers, including the very first layer.
In our CVPR version of PNN, the first layer uses 3x3 or 7x7 spatial convolution as feature extraction and all subsequent layers use the perturbative noise modules, as can be seen from our original PNN repo. Since MK has tried and implemented all-layer perturbative noise version of the PNN, we think it is helpful to provide our insights as well.
According to MK's repo (snapshot shown below), PNN with all uniform noise in all layers (including the first layer) achieves an accuracy of 72.6% accuracy on CIFAR-10. Here we provide one naive solution (without changing too much from MK's implementation) that can reach ~85-86% accuracy. We want to point out that this is still one of the many on-going research topics regarding PNN and we will report findings in our subsequent follow-up work.
We create a duplicate class called class PerturbLayerFirst(nn.Module) from class PerturbLayer(nn.Module) in order to treat the first-layer noise module differently from the noise modules in the rest of the layers. Most of the modification happens within class PerturbLayerFirst(nn.Module) as well as class PerturbResNet(nn.Module).
The main idea for the fix is that:
-
We need many more noise masks. Using 3 highly correlated (RGB channel) base images for creating 128 or 256 noise perturbed response maps is simply not enough. See here for the fix.
-
Choice of noise level is sub-optimal and needs to be amplified for the first layer. The first layer input and subsequent layers undergo different normalization in MK's implementation, and the dynamic range is quite different. See here for the fix.
So, after the modification, PNN with all-layer noise perturbation modules can reach 85.92%, as opposed to MK's 72.6% accuracy reported in his repo. As a sneak peek, by controlling the noise level at various layers in an optimal way, we are able to obtain higher accuracy. We will provide more details after further analysis.
python main.py --net-type 'perturb_resnet18' --dataset-test 'CIFAR10' --dataset-train 'CIFAR10' --nfilters 256 --batch-size 20 --learning-rate 1e-4 --first_filter_size 0 --filter_size 0 --nmasks 1 --level 0.1 --optim-method Adam --nepochs 450
As I have discussed in the PNN paper as well as in its supplementary, we obtain a relation between the noise level and the convolutional filter size, i.e. how many neighbors are taken into consideration when computing local convolution operation. In the context of PNN, one can think of the additive noise as the parameters of a mapping function that takes the one pixel on the input map to the corresponding one pixel on the output response map, just like in traditional convolution, within each local patch, the convolution operation would map the center pixel to a corresponding pixel in the response map, by involving all the neighbors of the center pixel through dot product with filter weights.
Both of these mapping functions can be thought of as a feature extraction method, or a way of taking measures. If the noise level is too small, we are not taking effective measures of the input. On the other hand, if the noise level is too big, the noise overshadows the signal and meaningful information from the input is lost. Therefore, having the correct amount of noise is crucial for PNN to work.
In the very first work of PNN, we still determine the noise level empirically.
During my final year of PhD studies, I have devoted some of my research effort to exploring new methods in deep learning that are statistically efficient and adversarially robust. This line of research started with our Local Binary Convolutional Neural Networks (LBCNN) paper in CVPR 2017. In LBCNN, we tried to answer this question: do we really need learnable spatial convolutions? It turns out, we don't. Non-learnable random convolution using binary or Gaussian filters + learnable channel pooling works just as well. Following this, the next natural question to ask is: do we really need spatial convolutions at all? Maybe another feature extraction technique (as simple as additive noise) + learnable channel pooling will work just as well? This is what the PNN paper is trying to shed some light on.
A quick detour. In fact, the first script to run in this repo already uses non-learnable random convolution in the first layer for PNN. Please see Line 513 in model.py. Readers can comment that line out, and it will then return to normal learnable convolution for the first layer. They reach the same level of accuracy.
The hybrid between learnable channel pooling (for combining response maps) and non-learnable convolutional filters allows us to rethink the role of convolutional filters in deep CNN models. Through various visual classification tasks, I have seen comparable performance between LBCNN and CNN. The feasibility of LBCNN may have shed some lights on the potentiality that we can get by without needing learnable convolutional filters, and random convolution with immutable filters and learnable channel pooling is all it takes to learn effective image representations.
Based on these observations, one natural way going forward is to completely replace the random convolution operation. Within each local patch, since it is a linear operation that involves neighbors of the center pixel and a set of random filter weights via dot product for creating a scalar output that somehow carries the local information i.e., mapping the center pixel to the corresponding output pixel in the response map, the simplest possible linear operation, as a replacement, can be additive random noise. This is the motivation behind the follow-up work of PNN, where I introduce a very simple, yet effective, module called a perturbation layer as an alternative to a convolutional layer. The perturbation layer does away with convolution in the traditional sense and instead computes its response as a weighted linear combination of non-linearly activated additive noise perturbed inputs.
Our experience with LBCNN shows that random feature extraction via random convolution together with learnable channel pooling in deep neural networks are able to learn effective image features, and we view the additive random noise in PNN as one simplest way of such random feature extraction.
As I am finishing up writing this markdown document, I can’t help reflect on what a journey the last 2 months have been. I had to admit, when MK decided to go public on Reddit, I was in a bit of a shock, especially after I had already agreed to look into that issue. Within a week, this post caught the attention of multiple mainstream tech/AI media in China. The post was shared across Chinese social media including news articles discussing this issue with over 1 million views. Some articles and comments were harsh, but some were reasonable and impartial. Tenacious as I am, I can’t say that I was not under pressure.
But I came to realize one thing, that as a researcher, standing up to public scrutiny is not an option, but a responsibility. For that, I really want to thank Michael, not only for spending the time and effort to re-create and verify a published method, but more importantly, speaking up when things did not match up. I firmly believe that it is through these efforts that we as a community can make real progress.
Also, I want to say a few words to young researchers just entering the field, or college students (high schoolers, yes!) who are about to enter the field of AI. Things like this do happen, but you should never be discouraged from open-sourcing your code or doing open research. This is the core reason our field of AI advances so fast. During my recent trip back to China, I get a chance to meet with a high school senior who was fervently talking to me about implementation details of Batch Normalization and Group Normalization. I was truly amazed. For all the young AI researchers and practitioners out there, I truly encourage you to think out of the box, don’t settle on the doctrines, explore the unexplored, travel the less traveled, and most importantly, do open research and share your code and findings. That way, you are helping the community move forward, even if it’s just one inch at a time.
So, let us keep searching, researching, and sharing.
Felix
Nov. 24, 2018
-
PNN Project Page: Perturbative Neural Networks (PNN)
-
Felix Juefei-Xu, Vishnu Naresh Boddeti, and Marios Savvides, Perturbative Neural Networks, in Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR), 2018.
-
@inproceedings{juefei-xu2018pnn,
title={{Perturbative Neural Networks}},
author={Felix Juefei-Xu and Vishnu Naresh Boddeti and Marios Savvides},
booktitle={IEEE Computer Vision and Pattern Recognition (CVPR)},
month={June},
year={2018}
}