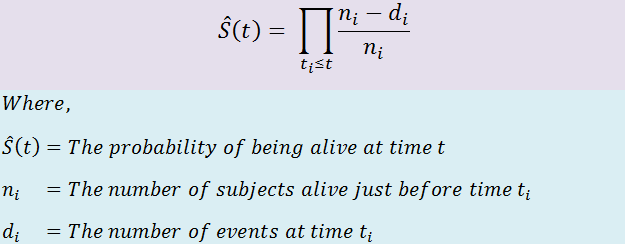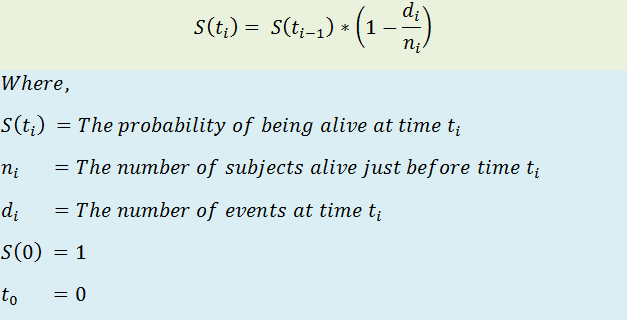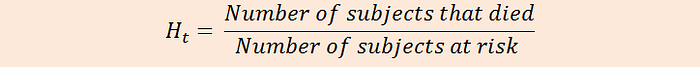Lung Cancer Survival Analysis

Table of Contents

• Project Objective
• Methods
• Technologies
• Getting Started
• Project Description
• Models Results
  • Kaplan-Meier Estimator
  • Nelson-Aalen
  • Log-Rank Test
  • Cox Regression
• License

Project Objective

The objective of the project is to estimate the time-to-death for patients diagnosed with lung cancer.

Methods

• Data Visualization
• Survival Analysis
  • Kaplan-Meier Estimator
  • Nelson-Aalen Estimator
  • Log-Rank Test
  • Cox's Proportional Hazard Model

Technologies

• Jupyter Notebook
• Python 3.8.1
• Python Packages
  • pandas
  • numpy
  • lifelines KaplanMeierFitter
  • lifelines NelsonAalenFitter
  • lifelines logrank_test
  • lifelines CoxPHFitter
• Python Virtual Environment

Getting Started

1. If necessary, install the python3-venv package using the following command: sudo apt install python3.8-venv
2. Create a virtual environment with: python3 -m venv survival-wkspc
3. cd into the survival-wkspace folder
4. Activate the environment: source bin/activate
5. Install python packages: python3 -m pip -r requirements.txt

Project Description

In oncology, typical questions to be answered are:

• What is the impact of specific clinical characteristics on patients' survival?
  • EG: Is there a difference between people who have high blood sugar and those who do not?
• What is the probability that an individual survives a specific time?
  • EG: Given a set of cancer patients, what is the probability that a patient will be alive at that time if some set of time has passed?
• What, if any, are the differences in survival between groups of patients?
  • EG: Compare the effects of two different treatments.

Survival Analysis Fundamentals:

• Survival Time - The amount of time until an event
  • Events could be birth, death, product failure, etc...
• Relapse - A deterioration in the subject's state of health after a temporary improvement
• Progression - The process of developing or moving gradually towards a more advanced state
• Data Censoring - Occurs when observations do not experience the event of interest
  • EG: In the study of a product's failure, some products might not fail
  • Right Censoring - Occurs when the subject under observation does not or has not yet experienced the event
    • EG: When studying death, a patient might still be alive
  • Left Censoring - Occurs when the event cannot be observed
    • EG: The event could have occurred before the study began
  • Interval Censoring - Occurs when the data is for a specific time interval
    • EG: The event of interest might occur before or after, but not during the study

Two related probabilities are used to analyze survival data:

1. Survival Function (S)
   • Defined as the probability that a subject survives from the diagnosis of a disease to a specified future time, t
   • Focuses on the survival of a subject
   • EG: S(200) = 0.7 means that after 200 days, a subject's probability of survival is 0.7
   • Kaplan-Meier Estimator is used to find the survival probability of a subject
2. Hazard Function (H)
   • Defined as the a subject under observation at time t has an event at time t
   • Focuses on the death of a subject
   • EG: H(200) = 0.7 means that on or after 200 days, the probability of death is 0.7
   • NOTE: The Hazard Function gives us the cumulative probability

Models Results

Kaplan-Meier Estimator

• Is a non-parametric statistic used to estimate the survival function from the lifetime data
• Often used to measure the fraction of patients living for a specific time after treatment or diagnosis
• These plots help to visualize survival curves

The probability of survival at time ti, S(ti), is calculated as follows:

More simply:

TODO: Talky stuff here

Nelson-Aalen Estimator

• Is a non-parametric statistic used to estimate hazard rates
• Often used to measure the fraction of patients who have died for at or by a specified time after treatment or diagnosis
• Aggregate information regarding survival can be visualized using the Nelson-Aalen hazard function, h(t). The hazard function gives us the probability that a subject under observation at time t has an event of interest at that time
• NOTE: The hazard rate CANNOT be found by transforming the survival rate

The cumulative probability of hazard at time t, H(t), is calculated as follows:

To calculate non-cumulative hazard probability at a specified time, t:

Log-Rank Test

• Is a hypothesis test that is used to compare the survival distributions of two samples with the goal of determining if there is any significant difference between the groups compared.
• The null hypothesis states that there is no significant difference between groups being studied.

Cox's Proportional Hazard Regression

• Is a regression model used, generally, by medical researchers to determine the relationship between the survival time of a subject and one or more predictor variables. It helps us to determine how different parameters such as age, sex, weight, height, etc.. affect the survival time of a subject.
• Unlike the Kaplan-Meier Estimator, the Nelson-Aalen Estimator, and the Log-Rank Test, Cox's Proportional Hazard Regression Analysis works for both categorical and non-categorical predictors.
• In short, it is used to determine how different factors impact the event of interest.
• Hazard Ratio (HR)
  • HR = value of exp(bi) from the Hazard Function
  • HR = 1 : No Effects
  • HR < 1 : Reduction in Hazard
  • HR > 1 : Increase in Hazard