This repository is based on Scipy's integrate module. The Radau method implemented in Scipy for solving ordinary differential equations (ODEs) is adapted to allow for the solution of differential-algebraic equations (DAEs) up to index 3.
This is done by introducing a mass matrix M and solving the following equation:
M dX/dt = f(t,X)
To use this package, execute the following command :
python setup.py develop
which will install the package as a development package, i.e. directly referring to the You can also install it as a normal package :
python setup.py install
But you loose the ability to modify the code on the fly without reinstalling the package...
To use the modified integrator:
from scipyDAE.radauDAE import RadauDAE
scipy.integrate.solve_ivp(..., method=RadauDAE)
Refer to the examples and to the documentation for more information.
Various test problems are given:
-
pendulum (index 3, 2, 1 or 0 DAE)
-
transistor amplifier (index-1 DAE with singular mass-matrix)
-
Roberston chemical system (stiff DAE of index 1, or stiff ODE formulation)
-
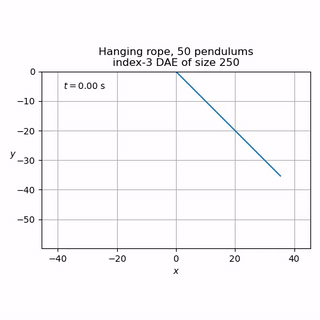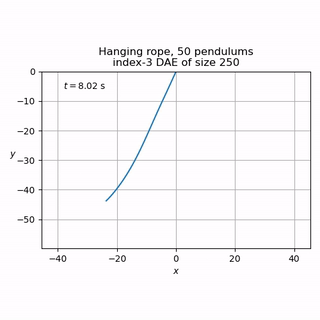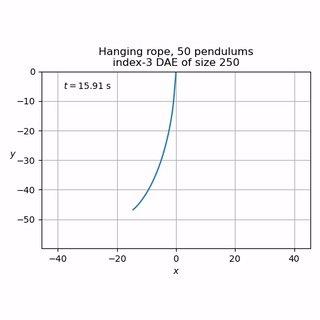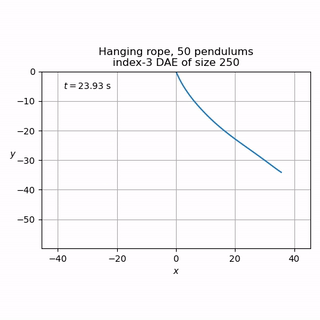
"recursive" pendulum (index-3 DAE of size n, n being the number of serially connected pendulums)
The latter may be used to simulate simple ropes, for example:
or even compute the "free falling chain" problem.
This modification of Radau will hopefully be pushed to Scipy after some further testing :)
Further DAE integrators with time adaptation (ESDIRKs) will be implemented based on Scipy's solver class. A test case with a DAE from a discretised PDE will also be added.
A very good reference to read: E. Hairer and G. Wanner, Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Equations 2nd Revised Edition 1996