Hidden Dimensions
Goal: Explore properties of Latent spaces to facilitate domain knowledge extraction in unsupervised/semi-supervised set-ups.
Data domains: Text and Image. Later on Graphs.
Applications:
- By discovering how to create Well-Clustered latent spaces, we can enable the extraction of Domain Constructs and Domain Concepts.
- Examples:
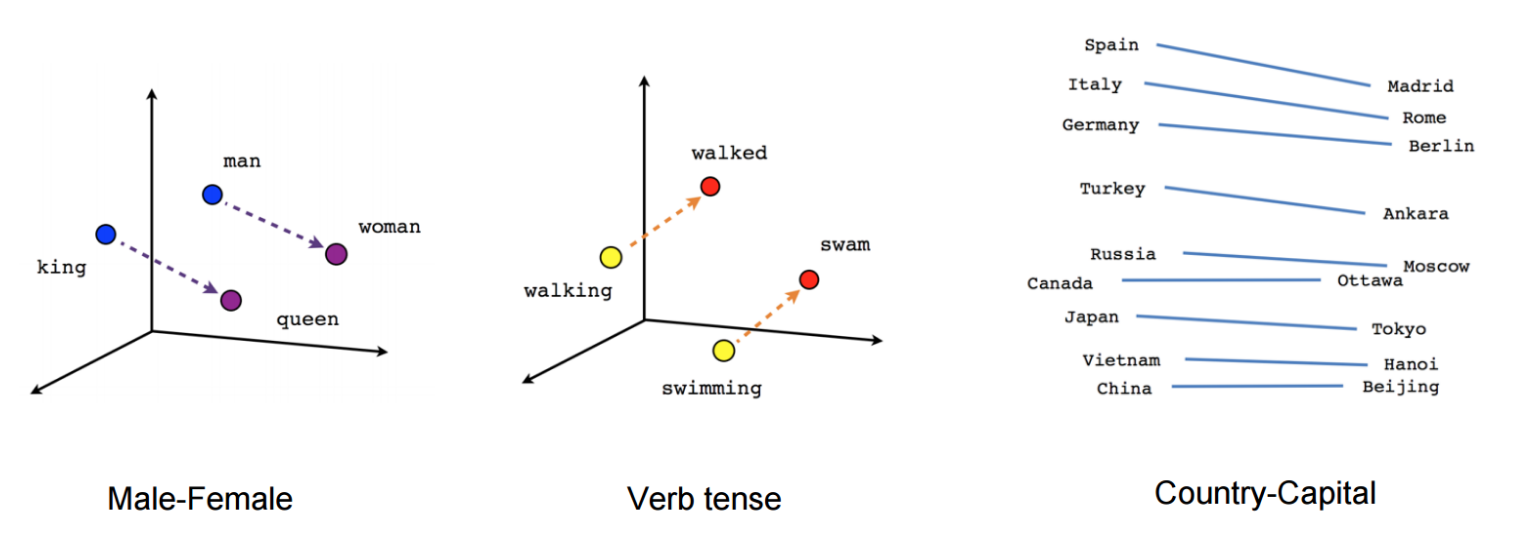
- Vector Directions in Word Embeddings
- Arithmetic on Image Embeddings
- By designing Algorithms for Navigation in a Meaningful latent space, we can imitate a generative process which might resemble abstract reasoning.
- Examples:
- Extracting hierarchies and relationships between objects from an image through traversal of sub-images directly in the latent space (Image embeddings);
- Writing code on top of pre-defined functionality by expanding parse trees directly in the latent space (Graph embeddings);
- The analogy to the human mind is that latent representations are thoughts derived from perceptual information.
- The navigation in the latent space then corresponds to thinking about thoughts, a mechanism which allows us to generate relevant actions which derive from an abstract representation of a situation, rather than exact copies of actions performed in the past in a similar situation.
Applications linked to our past research:
- Clustering Computer Programs based on Spatiotemporal Features
- Aster Project: AST derived Code Representations for General Code Evaluation and Generation
- Clustering and Visualisation of Latent Representations
- Learning Semantic Web Categories by Clustering and Embedding Web Elements
| Representation | Description |
|---|---|
 Wikipedia, Autoencoder |
The latent representation in a typical autoencoder is a kind of black box or bottleneck inside a system that optimizes the information compression of the input data constrained by minimizing the data reconstruction error. |
| Clustering | Data defined by some measurements. Example: position, color. |
 |
Discover structure in the data: |
| yellow dots | - left upper part |
| red dots | - left lower part |
| blue dots | - right lower part |
| (K-means) | Assigns N observations to K clusters. Number of clusters needs to be known beforehand. |
| - randomly pick representatives of clusters | |
| - assign datapoints to nearest representative | |
| - re-pick representatives based on newly formed cluster (closest to mean point) | |
| - re-iterate |
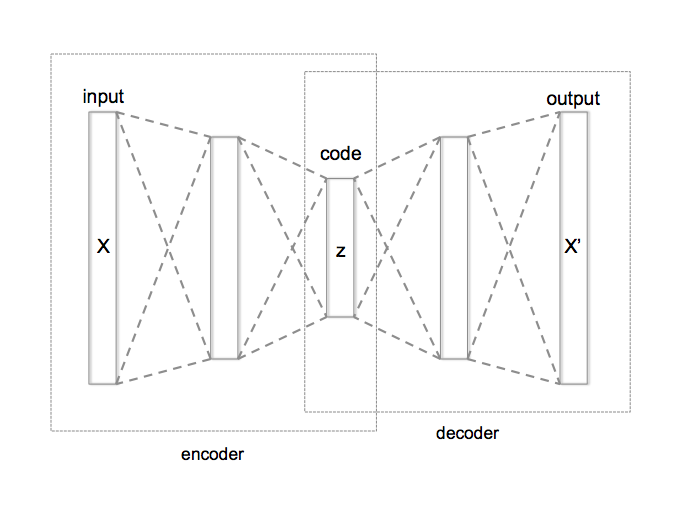
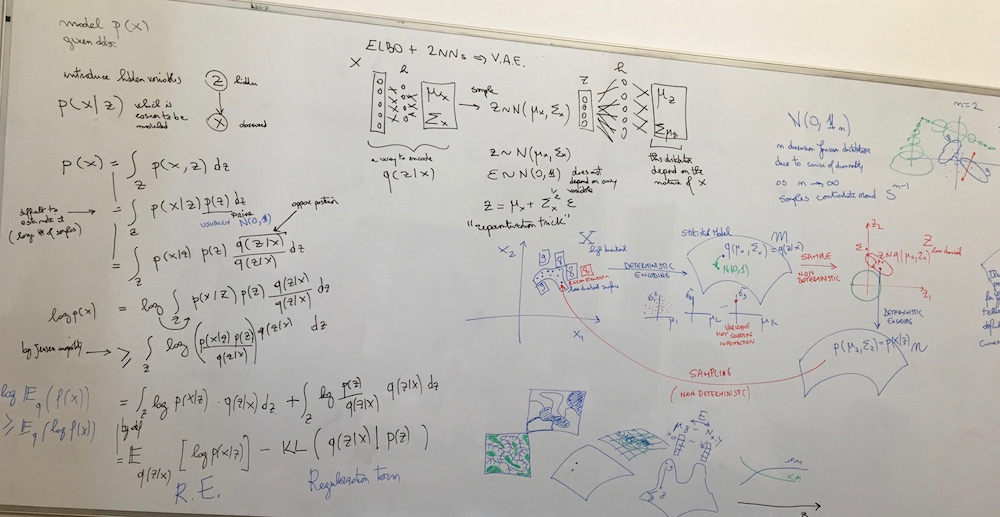
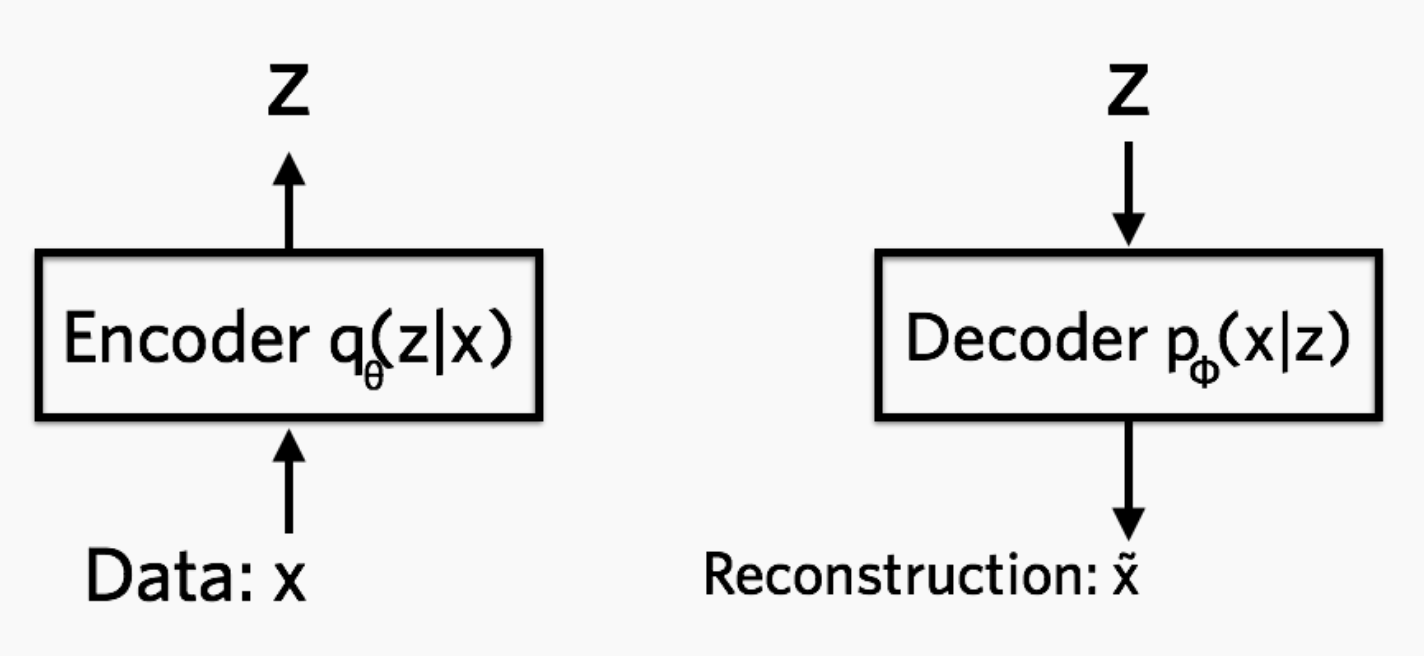
Idea: Model latent variable as a variable drawn from a learned probability distribution.
Result: By comparison to the autoencoder the latent space is continuous and interpolation between samples is possible. See VAE tutorial 1 for more explanations on this topic.
Key-words: Prior, posterior, probability distribution, log-likelihood, jensen inequality, re-parametrization trick, sampling from a distribution.
| Representation | Description |
|---|---|
 from VAE tutorial 2 |
Encoder: q models probability of hidden variable given data, Decoder: p models data probability given hidden variable |
 |
 |
|---|---|
| VAE Derivation: | VAE Properties: |
| Loss function consists of 2 terms - Reconstruction Error: how well samples are reconstructed from hidden variable, KL Divergence: penalizes data points from occupying distant regions in the latent space. | Encoding sample is deterministic. Then z is drawn from probability distribution q(z | x). Reconstructed ~x is also drawn from probability distribution p(x | z). |
| Representation | Description |
|---|---|
 |
Self-Organizing Maps are artificial neural networks where neurons are represented as cells in a grid. |
| competitive learning: neurons compete for activation - selection of best matching unit (BMU) | adaptive learning: neurons "spread knowledge" to their neighbouring neurons when activated - weights are adapted |
| Each input that we feed in the network will activate the neuron with the most similar weights to the input. | Each activation changes the surrounding neurons by adjusting their weights to be closer to the activated neuron. The closer the surrounding neuron is to the activated one, the stronger the adjustment is. |
Variables and Algorithm
- s = current iteration, L = iteration limit, D = input dataset
- t = index of vector in dataset, W = weight vectors
- v = index of node in the map, u = index of best matching unit
- theta(u,v,s) = neighbourhood function between u & v at iteration s
- alpha(s) = learning rate at iteration s
- Randomize W
- Pick D(t)
- Traverse each node v in the map
- Compute (euclidean) distance between W(v) and D(t)
- Record v with minimum distance as u
- Update W in the neighbourhood of the BMU (including itself) by pull them closer to the D(t)
- W(v,s+1) = W(v,s) + theta(u,v,s) * alpha(s) * (D(t) - W(v,s))
- Increase s and repeat while s < L
By exploring properties/biases of latent spaces, we can address the interpretability problem in DNNs [C1].
 |
 |
|---|---|
| Word2Vec (Mikolov et al. (2013)) | DCGAN (Radford et al. (2015)) |
| By training a binary classifier which predicts if two words are in context, word embeddings with properties representing gender and tense result. | Adversarial learning on image generation from random vectors results in latent representations obeying simple arithmetic. |
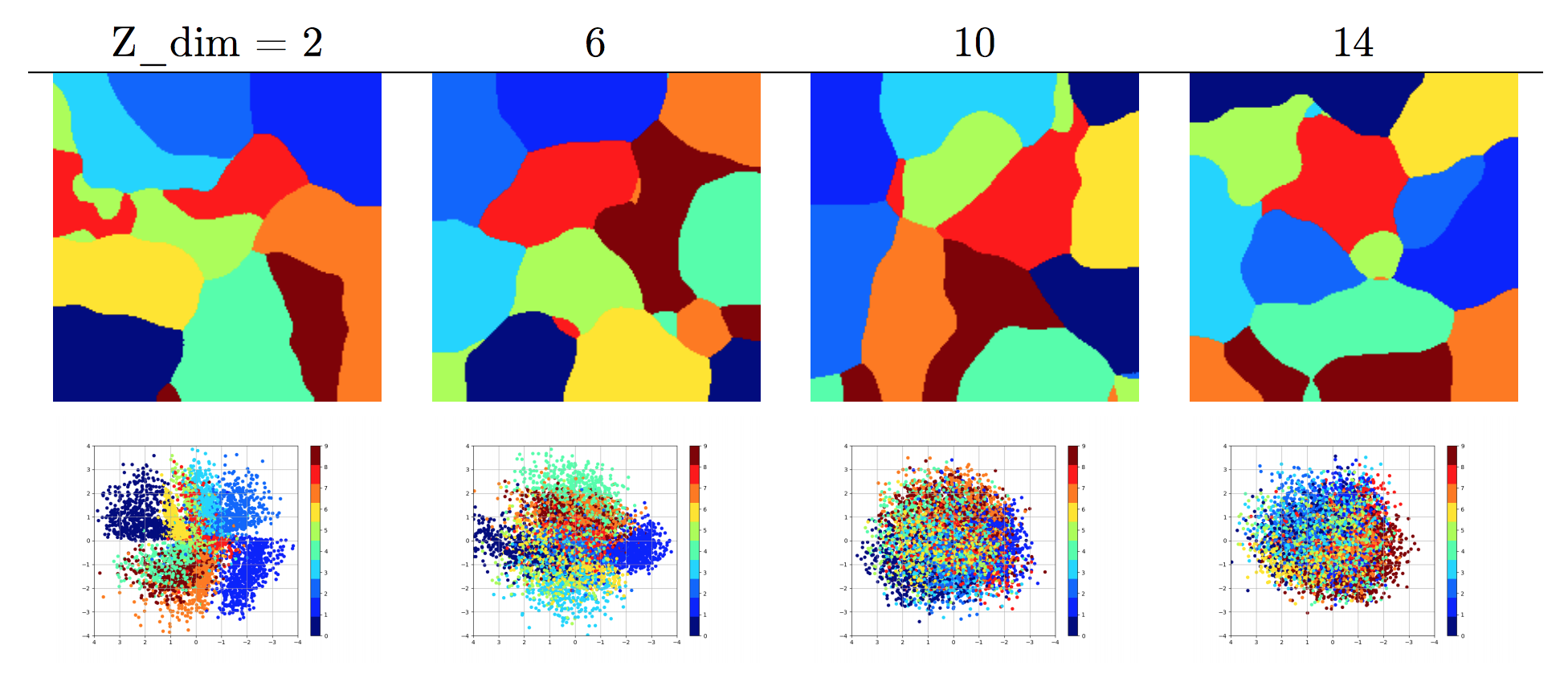
Description:
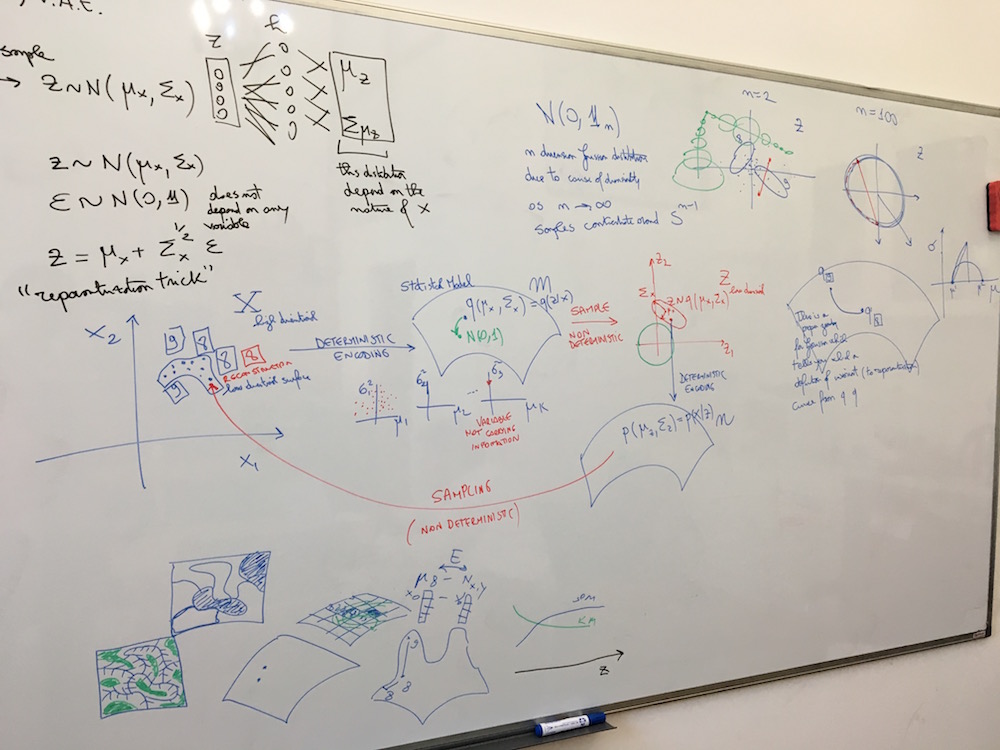
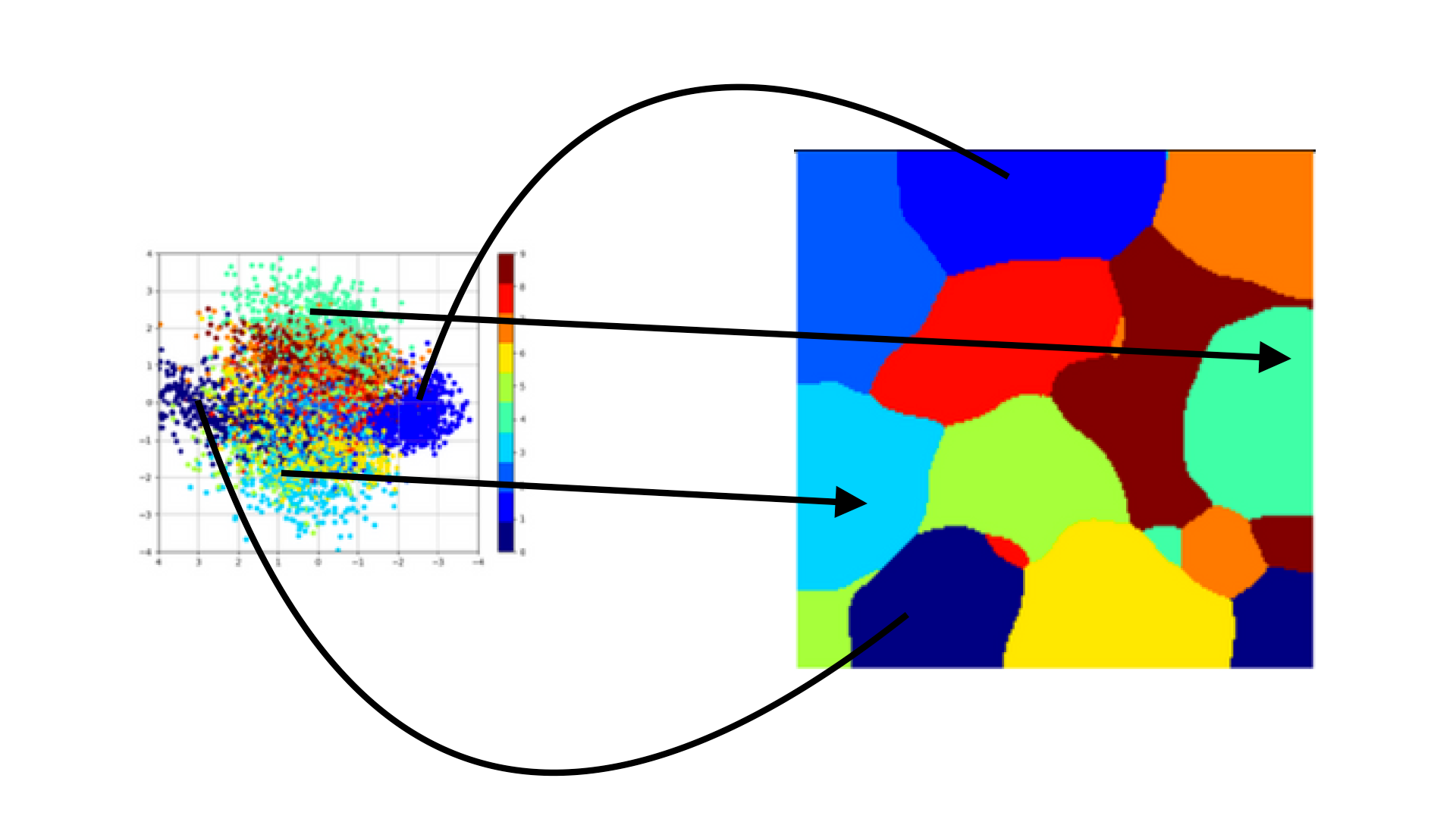
- SOM clustering (first row) and PCA (second row) 2D projection of latent MNIST as learnt by a VAE
- Z_dim = 2, latent representation of samples, no projection
- latent space becomes denser as Z_dim increases (see PCA)
- latent space can be remodeled (density changes) through topological projection (see SOM)
Observations regarding data complexity:
- only k principle components obtained from Z (latent space) will be meaningful (in the case of MNIST k between 10 and 20)
- clusters are well-formed even with limited training (based on homogeneity & silhouette scores and manual evaluation)
| Projection | Sub-spaces |
|---|---|
 |
 |
| VAE creates a very dense space, which is an advantage for continuity (eg. interpolation), but what about border regions? | Sub-spaces of the SOM-clustered latent space can be observed through the U-matrix - brighter border regions between clusters. |
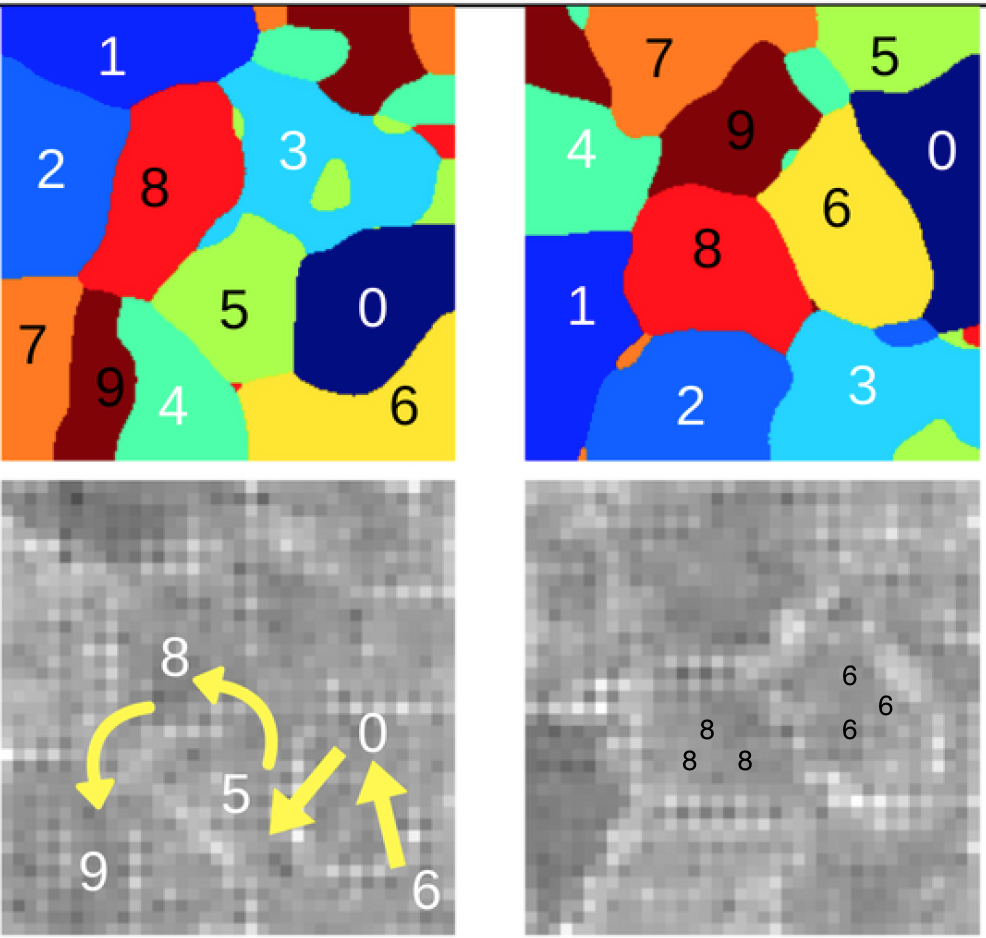
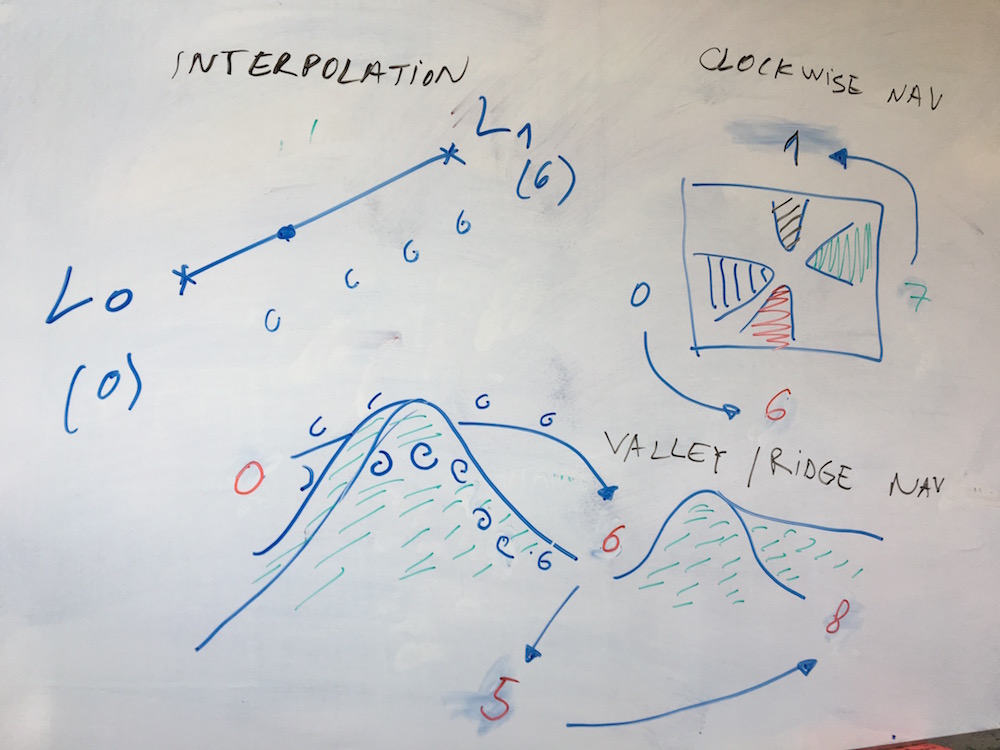
Application to latent interpolation:
- continuity means that we can have a smooth transition from a representation of the handwritten-digit 8 to a representation of handwritten-digit 6
- a common way to perform interpolation is the linear one, which assumes the latent representations to be in a euclidean space, where straight lines can be drawn from any point to any other point
- depending on the meaning of the latent representations, other distance measures and interpolation types might be necessary
- for the VAE case, the latent space is a manifold on gaussian distributions (see Fisher-Rao and Wasserstein geometries [M1])
Application to semi-supervised/few-shots learning:
- enclose landmarks (convex hull) defined by few labeled samples (few-shot learning) on clusters formed from latent representations of unlabeled data
- also, for data that belongs conceptually to the same class, yet exhibits variability in labels, clusters can help us identify similarities in these labels
 |
 |
|---|---|
| Latent Arithmetic: Do sub-images form hierarchical clusters or separate clusters in the latent space? Can header and container be added (with a learnt operator, in the latent representation) to output the latent resulting page? Can algorithms for navigation in the tree structure be directly implemented in the latent space? | Latent Navigation: Linear interpolation between Z of samples; Clock-wise rotation (interpolation on a curved surface); Valley/ridge navigation on projected surface of latent space - valleys/ridges can be found by clustering: dense regions form valleys, while sparse regions determine ridges (topology map). |
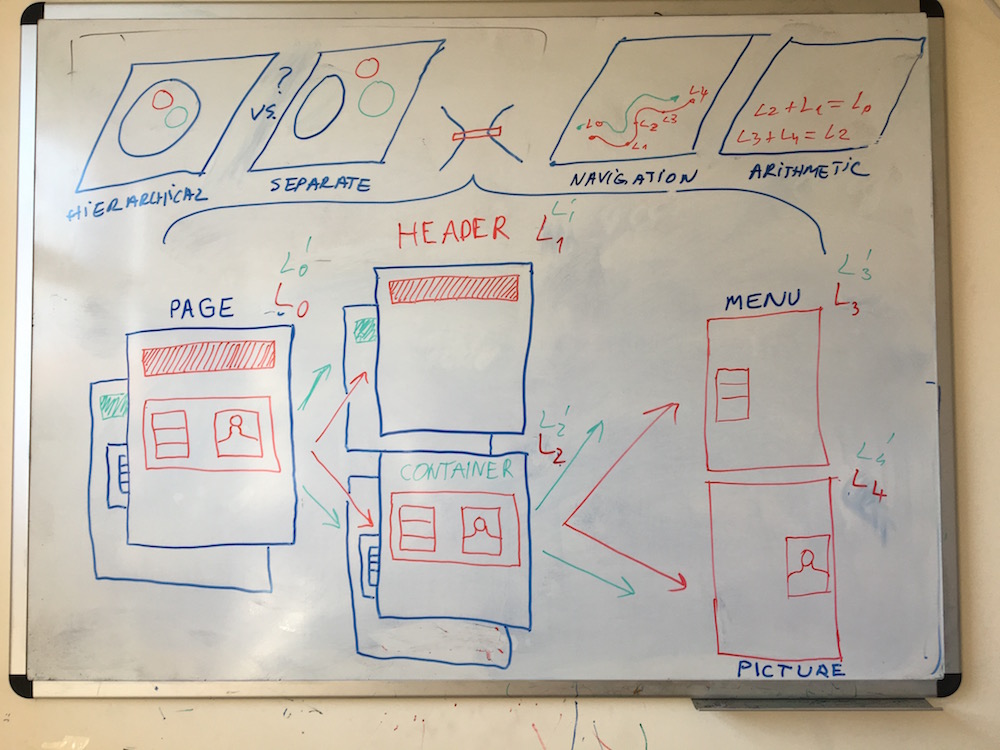
Application to structure extraction:
- suppose we would like to reconstruct the hierarchical data model that rendered an image
- examples range from screenshots of graphical interfaces to photo-realistic scenes
- in graphical interfaces: decompose a web page into main web elements - header and container with a left menu and a right grid with 3 buttons
- in photo-realistic scenes: a group of 3 people inside a car without doors on the right lane of a highway
- can a model trained with parts and segmented sub-parts shape the latent space such that decomposition of parts into sub-parts is possible?
- interpolation and composition as starting experiments, then structure extraction
Data domain: synthetic, image
Dataset:
- 28 x 28 x 3 sized images
- 2 labels: shape and color
- shapes: square, circle, triangle
- colors: red, green, blue
| Sample | Description | Sample | Description |
|---|---|---|---|
 |
red square |  |
red triangle |
 |
blue circle |  |
red circle |
 |
green square |  |
blue triangle |
 |
green triangle |  |
blue square |
Primary Goal:
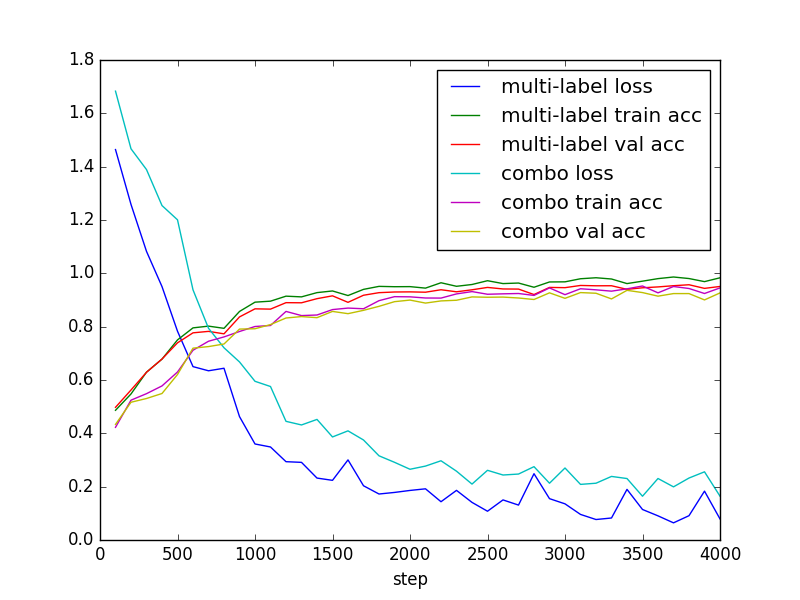
- explore multi-label, multi-class classification problem
- 3 options:
- multi-label (multiple logit sets)
- combination of labels (one logit set, each logit is a combo)
- one neural-network for each label
Secondary Goal:
- inspect learned features in intermediate CNN layers
| Primary Results | Primary Conclusions |
|---|---|
 |
Multi-label performs slightly better than combinations of all labels. The total number of logits add in the case of multi-label, but multiplies in the case of combinations. |
Data domain: synthetic, image and text
Dataset:
- 56 x 56 x 3 sized images
- 2 figures per image, obtained by concatenation of shape-color figures
- 2 relations: "above" and "next_to"
- for the latent arithmetic extension, also add images with only one figure
| Sample | Description |
|---|---|
 |
green square above blue square |
 |
green triangle above red square |
 |
blue circle next_to red square |
 |
green square next_to blue triangle |
Primary Goal: Test RNN for textual description of scenes.
Secondary Goal: Use attentional RNN to visualize the parts of the image the model looks at in order to generate a certain word in the description.
Resources: See [A1, A2] for visual attention models and [A3, A4] for text attention models.
Extension: Latent arithmetic with figures. What is the relation between the latent representation of an image with a circle on top of a square and the latent representation of sub-parts of the image (the image of a circle and the image of a square)?
More complex spatial relations:
| Sample | Description |
|---|---|
 |
3 circles, 1 square, 5 triangles |
 |
3 large red squares, one square on top of the other |
 |
2 large red squares, 3 triangles on top |
 |
2 circles, 2 squares and 5 triangles |
Data domain: synthetic, image and text
Purpose: Test mock models for CLEVR with less data.
Data domain: natural, image and text
| Sample | Description |
|---|---|
 |
3D objects rendered in a scene. Questions test spatial reasoning. |
| Questions | Answers |
| Are there an equal number of large things and metal spheres? | Yes |
| What size is the cylinder that is left of the brown metal thing that is left of the big sphere? | Large |
Premise: Question types include attribute identification, counting, comparison, spatial relationships, and logical operations.
Primary Question: Can we group similar questions together?
Secondary Question: Can we generate new questions that are relevant?
The dataset is a great subject for the application of Relational Networks [G1], which belong to the family of Graph Nets.
Tutorials:
Models that work well for this dataset could be extended to do some sort of programming through the following links.
Primary Idea: Question asking
- When writing code, programmers often ask questions about the state of the program and from the answers infer the next steps to take in order to accomplish their goal.
- For instance, in the world of objects, we might ask which figures to swap such that a certain order relation is satisfied.
Topics to explore further: which questions do you ask yourself when writing code/solutions to programming tasks?
Secondary Idea: Tangible programming
- A more concrete example would be to group objects in a sequence such that similar colors are consecutive.
- This would translate into asking a lot of questions similar to the ones showcased by the CLEVR dataset
Topics to explore further: tangible interfaces, embodied cognition and interaction.
Third Idea: Logical questions modeled through programming
- Does the first object have the same color as the second one?
- More generally, does the object on position i have the same color as the object in position i + 1
- Where is the first object to have red color? Are there any objects colored with red at all?
Fourth Idea: Causal inference from answers to logical questions
- If object on third position is yellow and object on sixth position is blue, swapping the two will result in which color on 6th position?
- Does the initial color on 6h position even matter?
- What if a pattern of movements always results the same output? How can such patterns be found?
- Can an agent model optimal behavior and generate such patterns?
- Model three levels proposed in the ladder of causation by Pearl [P1]: Association, Intervention and Counterfactuals
- Does curiosity help?
Data domain: synthetic, image, tree and text
| Webpage | Element masks |
|---|---|
 |
 |
Description: This dataset was used to compare the results of models which infer html code from web page screenshots. An initial experiment compared the end-to-end network (pix2code) with a neural network for web elements segmentation and a tree decoding based on overlaps.
Extension: Latent arithmetic with web elements
| Header | + | Menu | + | Grid | = | Page |
|---|---|---|---|---|---|---|
 |
+ |  |
+ |  |
= |  |
Data domain: natural, image
Primary Idea: Clustering of latent representation
Secondary Idea: Latent interpolation
Third Idea: Few-shots learning after unsupervised training
[A1] Recurrent Models of Visual Attention, V. Mnih et al, 2014
[A2] Show, Attend and Tell: Neural Image Caption Generation with Visual Attention, K. Xu et al, 2016
[A3] Neural Machine Translation by jointly Learning to Align and Translate, D. Bahdanau et al, 2015
[A4] Effective approaches to Attention-based Neural Machine Translation, M. Luong et al, 2015
[C1] Cognitive Psychology for Deep Neural Networks: A Shape Bias Case Study, S. Ritter et al, 2017
[G1] A simple neural network module for relational reasoning, A. Santoro et al, 2017
[M1] A Comparison between Wasserstein Distance and a Distance Induced by Fisher-Rao Metric in Complex Shapes Clustering , A. De Sanctis and S. Gattone, 2017
[P1] [The Book of Why: The New Science of Cause and Effect] Judea Pearl, 2018.