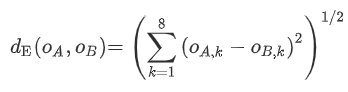Five Degree-of-Freedom Grain Boundary Interpolation

Code related to meshing, interpolation, and distance calculations of grain boundaries by representing 5DOF of grain boundaries as grain boundary octonions (GBOs) and mapping them into a Voronoi Fundamental Zone (VFZ). (https://github.com/sgbaird-5DOF/interp)

^{Figure adapted based on table of contents from DOI: 10.1016/j.commatsci.2021.110756 (a) 2D analogy of a Grain Boundary Octonion Voronoi Fundamental Zone (GBO-VFZ) with dark blue points within the VFZ, with the VFZ defined by the reference point (white) and Oh point group. (b) grain boundary energy (GBE) values plotted continuously between two arbitrary grain boundary octonions (i.e. changes in all 5DOF). (c) Hexagonally binned parity plot of GPR predictions colored by number of points per bin, log colorscale.}

We go over dependencies, getting started instructions including installation, basic usage, distance calculations, plotting, and using custom datasets. Finally, we go over the file dependencies (no additional installation needed), short descriptions of various files in the repository, advanced installation, and citing information.

To quickly navigate the README table of contents, use the table of contents button at the top-left of the GitHub README window.

Dependencies

MATLAB Version

MATLAB R2019b or higher (mainly for the arguments ... end syntax checking at the beginning of functions, which is used extensively throughout).

R2007a - R2019a

I suggest removing the arguments ... end syntax for any functions that use this and replacing it with corresponding inputParser() and varargin code to deal with variable input arguments, default parameter values, and repeating arguments. Alternatively, you could remove the arguments ... end syntax lines for each function and update every place that the function is called so that all input arguments are specified. Open up an issue if you need more details on this. Other functions may need to be replaced if they aren't available in early MATLAB versions.

MATLAB Toolboxes

Statistics and Machine Learning Toolbox (for Gaussian Process Regression: fitrgp(), fitrgp.predict())
Parallel Computing Toolbox (parfor, optional)
Symbolic Math Toolbox (optional, for numStabBary.m)

Files

See File dependencies for a list of files that interp5DOF.m depends on.

Getting Started

Quick Installation

The quickest way to install the code is downloading and unzipping the latest release or latest version, add all subfolders of interp to the path via addpath(genpath(".")), and make sure it's working by running interp5DOF_test. For additional details or development instructions, see advanced installation.

Basic Usage

See interp5DOF.m, which is a high-level function for Gaussian Process Regression (GPR), barycentric, nearest neighbor (NN), and inverse-distance weighting (IDW) interpolation. This involves importing/generating data and computing an interpolation.

interp5DOF.m can be called in other functions/scripts to produce interpolation results using 5DOF misorientation/boundary plane normal pairs (qm/nA) and grain boundary property values. It was written with loosely similar input/output structure to the MATLAB built-in function interpn() involving input points and values, query points and values, and options.

For a short description of the various functions included in this repository, see Contents.m or this section.

Simple Example Data

Separate from interp5DOF_test.m, the following is a fast, bare-bones example to show the basic input/output format of interp5DOF.m. See also get_cubo.m

cd code/
addpath(genpath("."))
npts = 100;
qm = get_cubo(npts); nA = normr(rand(npts,3)); %random (qm,nA) pairs
propList = 1:npts; %property values
qm2 = get_cubo(npts); nA2 = normr(rand(npts,3)); %random (qm,nA) pairs
method = 'gpr'; %interpolation method
[propOut,interpfn,mdl,mdlpars] = interp5DOF(qm,nA,propList,qm2,nA2,method)

Test functions

Most functions have a corresponding "test" function (e.g. hsphext_subdiv.m --> hsphext_subdiv_test.m, interp5DOF.m --> interp5DOF_test.m) which gives simple usage example(s). These are useful for debugging, visualizations, and understanding the functions without having to do a full run which could be time-consuming. This also allows for the non-test function code to be more succinct, as certain plotting routines can be moved to the test function instead. The various test functions generally run to completion within a few seconds, and the parameters can generally be changed freely (e.g. dimension, number of points). Some test functions have specific plotting routines for 1-sphere (2D) and 2-sphere (3D) cases since a 7-sphere is difficult to visualize and interpret (n-sphere). For example, see sphbary_test.m and toBPFZ_test.m.

Distance Calculations

If you only want to (manually) compute distances in the VFZ sense, first you need to map all GBs into a VFZ.

npts = 100;
o = get_ocubo(npts); %generate some random data
o = get_octpairs(o); %symmetrize (using default reference GBO), vecnorm(o(1,:)) == ~sqrt(2)
o = normr(o); % normalize

At this point, you can get the VFZ pairwise distance matrix via:

pd = pdist(o);
mat = squareform(pd);

The units will be the same as is given by eq.(1) from DOI: 10.1016/j.commatsci.2021.110756.

To convert to the traditional GBO distance, multiply $d_E$ by a factor of 2.

Alternatively, pdist2() may be of interest if you want pairwise distances between two sets of points, or vecnorm() if you want to calculate distances between two lists of GBOs:

npts2 = 100;
o1 = get_ocubo(npts1);
o1 = get_octpairs(o1);
o1 = normr(o1);

o2 = get_ocubo(npts2);
o2 = get_octpairs(o2);
o2 = normr(o2)

d = vecnorm(o1-o2,2,2); %o1 and o2 need to be the same size

If you want the "true" minimum distances (i.e. essentially the same implementation as GB_octonion_code, but vectorized and parallelized), you may use GBdist4.m directly with two sets of GBOs.

d = GBdist4(o1,o2,dtype="norm");

It depends on the application, but if you want to compute large pairwise distance matrices that are nearly identical to the traditional GBO distances, I recommend using the ensembled VFZ distance via ensembleGBdist.m with K >= 10.

d = ensembleGBdist(o,o2,dtype="omega")

This will be much faster than using GBdist4.m. For reference, this corresponds to (from the main paper when K==10):

This is distinct from ensembleVFZO.m, which takes the average interpolated property from K different VFZs.

Open an issue if you have something you'd like to do or something you'd like to clarify, but can't figure out among the (many) options and functions in the interp repo. With a few details, there's a good chance I can offer some suggestions that will save a lot of time.

Plots

Most plots in the paper are produced in the script: plotting.m. First, you need to create a dummy folder:

mkdir interp/code/interp5DOF-paper/figures/

The larger file dependencies, gitID-0055bee_uuID-475a2dfd_paper-data6.mat and gpr46883_gitID-b473165_puuID-50ffdcf6_kim-rng11.mat can be downloaded at figshare and have the following citation:

@misc{baird_homer_fullwood_johnson_2021, title={Five Degree-of-Freedom Grain Boundary Interpolation}, url={https://figshare.com/articles/dataset/gitID-0055bee_uuID-475a2dfd_paper-data6_mat/14405924/3}, DOI={10.6084/m9.figshare.14405924.v3}, abstractNote={These are larger MATLAB .mat files required for reproducing plots from the sgbaird-5DOF/interp repository for grain boundary property interpolation. gitID-0055bee_uuID-475a2dfd_paper-data6.mat contains multiple trials of five degree-of-freedom interpolation model runs for various interpolation schemes. gpr46883_gitID-b473165_puuID-50ffdcf6_kim-rng11.mat contains a Gaussian Process Regression model trained on 46883 Fe simulation GBs.}, publisher={figshare}, author={Baird, Sterling and Homer, Eric R and Fullwood, David and Johnson, Oliver K.}, year={2021}, month={Apr} }

Data Preparation

Input GBs can take on the following forms:

misorientation (qm) / boundary plane normal (nA) pairs
octonions (o)

Prediction GBs have a 2 appended, as in qm2. The inputs are stacked vertically (i.e. 1st row corresponds to 1st GB, 2nd row to 2nd GB, etc.).

Data can be converted between forms/conventions using the various rotation functions available in the repository (modified versions of GB Octonion Code). See also:

For an example of converting real literature data for Ni and Fe grain boundaries to octonions, see code/Kim2oct.m.

Active vs. Passive Rotation Convention

Active rotation is specified with an input parameter 'epsijk' == 1 and is the default used throughout the work. Passive rotation, in theory, can be specified via epsijk == -1 which should be propagated throughout the entire codebase via the top-level input, but this has not undergone the same extensive testing as the active rotation convention. To convert from the passive to the active rotation convention, I suggest converting the GB into octonion form and applying qinv.m to each grain boundary, that is:

o = [qinv(o(1:4,:) qinv(o(5:8,:))];

or simply

o = oflip(o);

parfor loops

Parfor loops are used by default where there is potential for significant speed-up. A parfor-compatible text progress bar is encoded into many of these. Adding disp() or fprintf() inside the parfor loop (aside from what's already inside the nested text progress bar function) may cause odd behavior on the command line output, but should not affect the integrity of the code execution. Because the parfor-compatible text progress bars need to be nested functions, in order to deal with the inability to add variables to static workspaces while debugging, you can either assign variables to "ans" (a special variable that is still accessible), output statements directly to the command line terminal (no variable assignment). Alternatively, you can comment the nested function, nUpdateProgress().

If the parallel computing toolbox is not installed, the parfor loops will execute as regular for loops. If the parallel computing toolbox is installed and you only want to use a single core, start a parallel pool with only one core before running any of the functions via parpool(1). The loop will still run internally as a parfor loop, however. A parfor loop with a single core and parallel computing toolbox should not run any slower than a regular for loop as long as they are contained within functions. A parfor loop executed within a script, however, is likely to result in significant slow-down.

To debug within a parfor loop, simply change it to a for loop while debugging and change it back afterwards. I added "parfor compatible" as a comment next to the parfor statements. Thus, you can use MATLAB find files (Ctrl+Shift+F) to search for the keyword "parfor compatible" (including quotes) in order to keep track of which parfor loops have been changed to for loops. If you make changes and an error arises, it is possible it will only give useful information at the top-level where the parfor started, hence the debugging suggestion above.

File dependencies

Take a look at parseReqFiles_test.m for generating a list of file dependencies for interp5DOF.m (below) or other files.

Contents.m (short descriptions)

Version as of Nov 3, 2020. See Contents.m for latest version.

File (.m)	Description
`addpathdir.m`	add folders of filenames using addpath() and dir()
`allcomb.m`	All combinations (Cartesian Product)
`axpolytope.m`	Indices of a polytope with vertices on every axis and every intersection of every plane formed by axes.
`axpolytope_test.m`	generate vertices on the axes of a polytope in n-D
`chebycenter.m`	Compute Chebyshev center of polytope Ax <= b.
`constant_colorbar.m`	script to generate a colorbar with constant limits
`constructGBMatrices.m`	Make Olmsted GB matrices for GB5DOF using labframe quaternion/normal inputs
`correctdis.m`	convert to disorientation (for plotting)
`cprnd.m`	Draw from the uniform distribution over a convex polytope.
`datagen.m`	generate octonion data for various literature datasets (or
`datagen_setup.m`	setup for generating octonion data (random or from literature)
`datagen_test.m`	test generation of octonion data
`degdelaunayn.m`	compute delaunay triangulation of d-1 hyperplane in d-dimensions
`disorientation.m`	determines the unique misorientation between two adjacent
`DisplayRequiredFunctions.m`	List required files and toolboxes. Displays them in the command window or console window (if deployed).
`dynamicCellExample.m`	Dynamically creating a nested cell structure (unfinished/deprecated)
`facet_subdiv.m`	Project a facet from n-dimensional space to a simplex in n-1
`facet_subdiv_test.m`	SUBDIV_TEST e.g. subdivide a d-1 or d-2 simplex (e.g. triangle or line in 3D Cartesian coordinates) and plot
`findgeometry.m`	FINDGEOMETRY: Output the misorientation FZ geometry of a point given a quaternion (e.g. 'OAB').
`findgeometry_test.m`	test findgeometry for 'OAB', 'OBCE', 'OADE', etc. of misorientation FZ
`fz_inserter.m`	Compute misorientations in the fundamental zone for two lists of orientations
`GB5DOF.m`	computes the energy of an arbitrary boundary in FCC metals (BRK energy function)
`GB5DOF_setup.m`	Compute 5DOF GB energy from BRK function
`GB5DOF_setup_test.m`	GB5DOF_setup test
`GBdist2.m`	troubleshooting for GBdist() (deprecated)
`GBdist3.m`	troubleshooting for GBdist() (deprecated)
`GBdist4.m`	modified version of GBdist function by CMU group. Keeps o1 constant.
`GBdist4_r2018a.m`	arguments
`GBdistdis.m`	modified version of GBdist() (deprecated)
`GBdistEucl.m`	modified version of GBdist() for Euclidean distances (deprecated)
`GBlab2oct.m`	convert lab coordinate grain boundareis to octonions
`GBlab2oct_test.m`	Test from GB Octonion Tutorial script
`GBoct2five.m`	(incorrect, derivation error, 2020-11-03) Inverse operation of GBfive2oct.m (GB_octonion_code), output "five" struct
`GBoct2five_r2018a.m`	arguments
`GBoct2five_test.m`
`GBoct2five_test2.m`
`GBpair.m`	(deprecated) Method 1: Find o3 that has the minimum summed distances, o1-->o3, and o2-->o3.
`GBpair2.m`	deprecated
`GBpair_r2018a.m`	arguments
`GBpair_test.m`	test
`gcfpos.m`	get current figure position and copy to clipboard
`get_cubo.m`	get n quaternions from randomly or uniformly sampled cubochoric points
`get_cubo_r2018a.m`	arguments
`get_errmetrics.m`	get various error metrics for measured data relative to
`get_failed.m`	find failed jobs (under construction)
`get_failed_test.m`	test getfailed.m
`get_fname.m`	Get a filename to load or save (deprecated, specific to old naming scheme)
`get_interp.m`	Interpolate query point values based on spherical or planar barycentric coords in a mesh
`get_octpairs.m`	Get a set of octonions that are symmetrized with respect to a fixed reference GB (rng seed == 10)
`get_octpairs2.m`	deprecated version of get_octpairs()
`get_octpairs_r2018a.m`	arguments
`get_octpairs_test.m`	get_octpairs test
`get_ocubo.m`	get octonions formed by pairs of quaternions from randomly or uniformly sampled cubochoric points.
`get_ocubo_r2018a.m`	arguments
`get_ocubo_test.m`	get_ocubo test
`get_omega.m`	calculate octonion distance
`get_omega_r2018a.m`	arguments
`get_repsets.m`	Find sets of points with at least a degeneracy of n
`get_repsets_test.m`	nonunique test
`get_sympairs.m`	get all combinations (pairs) of operators for a point group
`get_sympairs_r2018a.m`	arguments
`hsphext_subdiv.m`	Hypersphere exterior hull subdivision.
`hsphext_subdiv_test.m`	hypersphere exterior hull subdivision test
`hypercube.m`	Calculate vertices and convex hull triangulation of a hypercube
`hypercube_test.m`	hypercube test
`hyperquadrant.m`	Generate n-dimensional Ellipsoid or Sphere
`hypersphere.m`	Generate n-dimensional Ellipsoid or Sphere
`hypersphere_subdiv.m`	Subdivide a "spherical" convex hull and collapse the triangulation.
`hypersphere_subdiv_test.m`
`hypersphereSetup.m`	wrapper function for hypersphere.m, includes 'orthant' option
`inBPFZ.m`	return logical of which boundary plane normals are in BP fundamental zone
`InCubicFZ.m`	Test whether or not a set of rodrigues vectors is within the cubic misorientation fundamental zone.
`inhull.m`	tests if a set of points are inside a convex hull
`inhull_setup.m`	wrapper function for inhull (deprecated)
`inmisFZ.m`	check which rodrigues vectors fall inside the misorientation fundamental zone via vert2con (FEX)
`inmisFZ_test.m`	inmisFZ test
`insertrows.m`	Insert rows into a matrix at specific locations
`interp5DOF.m`	Convert misorientation and boundary plane normal 5DOF input
`interp5DOF_setup.m`	setup for interpolating five-degree-of-freedom property
`interp5DOF_test.m`	interp5DOF test
`interpplot.m`	Create parity plot with 5DOF plots on side (deprecated)
`intersect_facet.m`	Find intersection of ray with facet using barycentric coordinates.
`intersect_facet_test.m`	intersect facet test
`ismembc_test.m`	ismembc vs. ismember test
`knninterp.m`	compute linear interpolation using hyperplane fitted to k-nearest neighbors
`knninterp_test.m`	knninterp test
`mesh5DOF.m`	generate "five" and "o" for a five degree-of-freedom fundamental zone (deprecated)
`meshBP.m`	generate boundary plane (BP) fundamental zone mesh for a
`meshBP_test.m`	test meshBP
`meshFZ.m`	mesh the misorientation fundamental zone (issues with tetgen)
`meshgen.m`	generate octonions randomly or from literature (deprecated)
`meshgen_test.m`
`misFZcon.m`	get constraints for misorientation fundamental zone (misFZ)
`misFZcon_test.m`	misFZcon test
`mustBeSqrt2Norm.m`	check that first octonion in list has norm == sqrt(2) and each quaternion has norm == 1
`mustContainFields.m`	check fieldnames(S) and make sure every checkname exists
`myismember.m`	do an ismembertol by rows with set precision and tolerance
`n2c.m`	t = num2cell(pts,1)
`n2cplot.m`	convert rows of points to cells of points, convenient for plotting.
`normr.m`	normalizes vectors row-by-row. Outputs zero vector if zero vector input (shadowed by Computer Vision Toolbox)
`numStabBary.m`	a numerically stable barycentric approach in high dimensions
`numStabBary_example.m`
`numSubplots.m`	Calculate how many rows and columns of sub-plots are needed to neatly display n subplots
`Oh_pg.m`	Oh point group load/testing function
`optimize_zeta.m`	Minimize the pairwise distance matrix of a set of GBs w.r.t. zeta (twist angle via U(1) symmetry)
`optimize_zeta_r2018a.m`	arguments
`optimize_zeta_test.m`	optimize_zeta test
`optimize_zeta_test_r2018a.m`	optimize_zeta test
`orthoplex.m`	Find indices and convex hull triangulation of an orthoplex
`orthoplex_test.m`	orthoplex test
`OSLERP_setup.m`	script to call OSLERP (deprecated)
`OSLERP_setup2.m`	another script to call OSLERP (deprecated)
`osymset.m`	get symmetrically equivalent octonions
`osymset_r2018a.m`	arguments
`osymsets.m`	Get symmetrically equivalent octonions (osymsets) for each octonion in a list of octonions
`osymsets_r2018a.m`	arguments
`parityplot.m`	Create a parity plot and pass options to (scatter() or hexscatter()) and refline().
`parseReqFiles.m`	parse required files & products using fileseparator sep
`parseReqFiles_test.m`	parseMyFiles_test
`pd_sse.m`	get the error of a pairwise distance matrix relative to the true pairwise distance matrix
`pd_sse_r2018a.m`	arguments
`plot5DOF.m`	plotting five degree-of-freedom parameters in misorientation and boundary plane spaces
`plotFZrodriguez.m`	define the FZ vertices
`plotFZrodriguez_test.m`	PLOTFZRODRIGUEZ_TEST
`plotFZrodriguez_vtx.m`	plotFZrodriguez with 'A','B','C','D','E','O' vertices
`proj_down.m`	project down by removing null dimensions (i.e. a rotation and translation) via singular value decomposition
`proj_down_r2018a.m`	arguments
`proj_down_test.m`
`proj_up.m`	project up (restore null dimensions) using "USV" struct from proj_down.m
`projfacet2hyperplane.m`	project facet vertices onto a hyperplane defined by nvec
`projfacet2hyperplane_test.m`	project facet to hyperplane test
`projray2hyperplane.m`	Project ray (pt) from unit hypersphere to tangent hyperplane at another point (nvec)
`projray2hyperplane_test.m`	project ray to hyperplane test
`projray2hypersphere.m`	project ray to hypersphere, compute barycentric coordinates, compute intersecting facet
`projray2hypersphere_test.m`	project ray to hypersphere test
`randOctParityData.m`	submit sets of jobs to supercomputer or run locally for interp5DOF()
`readNODE.m`	Read vertex positions from .node file, .node files are used by Stellar and Triangle
`rescale_test.m`	rescale test (test of built-in function)
`rotationmat3D.m`	creates a rotation matrix based on axis and angle
`RotMatrix.m`	N-dimensional Rotation matrix
`roundp.m`	rounds values in x to n digits past the decimal sign.
`run.m`	runRun MATLAB script
`run2.m`	run test
`sbatch_setup.m`	setup for SLURM sbatch submissions (deprecated)
`simplex_subdiv.m`	Compute the subdivision cartesian coordinates of a simplex
`slightRot.m`	rotate points slightly in every dimension
`slightRot_test.m`	slight rotation matrix test
`sphbary.m`	compute spherical barycentric coordinates of a facet or simplex [1]
`sphbary_setup.m`	sphbary coords and intersections for points
`sphbary_test.m`	spherical barycentric coordinates test
`sphconvhulln.m`	Compute the "convex hull" on a spherical surface
`sphconvhulln_test.m`	spherical convhulln test
`sphere_stereograph.m`	compute the stereographic image of points on a sphere.
`sphere_stereograph_inverse.m`	compute stereographic preimages of points.
`sphere_stereograph_test.m`	sphere stereograph test
`sphere_stereographic_inverse_testsphere.m`
`stereographic inverse test.m`
`sphtri_subdiv.m`	Subdivision scheme that segments the triangle formed by vertices of a spherical triangle
`sphtri_subdiv_test.m`
`sqrt2norm.m`	take a set of octonions and give each row norm == sqrt(2) if (norm == 1) \|\| (norm == sqrt(2))
`sqrt2norm_r2018a.m`	arguments
`symaxis.m`	Return the symmetry axes (if multiple) and the geometry given a quaternion
`symaxis_test.m`	{
`tblvertcat.m`	vertically catenate tables with different variables, filling in dummy values as needed
`tblvertcat_test.m`	tblvertcat_test
`testForGBFZSymmetryPlot.m`
`toBPFZ.m`	Rotate an arbitrary boundary plane normal for quaternion into standard boundary plane fundamental zone
`tofiveFZ.m`	Take 5DOF data and rotate it into misorientation and boundary plane fundamental zones.
`tricollapse.m`	collapse triangulation of points (i.e. a triangulation involving repeat points).
`vecpair2rmat.m`	Compute a (non-unique) rotation matrix to go from v1 to v2.
`vert2con.m`	convert a set of points to the set of inequality constraints
`vert2lcon.m`	An extension of Michael Kleder's vert2con function, handles degeneracy
`write_video.m`	write a set of images to a video named movname with some defaults
`write_video_test.m`
`zeta_min2.m`	ZETA_MIN Alternative version of CMU group function zeta_min(), vectorized by Sterling Baird
`zeta_min2_r2018a.m`	arguments
`GBoct2mat.m`	convertion grain boundary octonions to orientation matrices (unfinished)
`Kim2oct.m`	load Kim2011 dataset, convert to norm-symmetrized octonions
`avgrepeats.m`	average values for duplicate points, remove all but one from degenerate set
`avgrepeats_test.m`	avgrepeats test
`bugtest.m`	checking a "bug" (turns out actually intended) with arguments..end syntax
`el2po.m`	elevation angles to polar angles
`el2po_test.m`	po2el_test
`get_alen.m`	get arclength of sphere (acos of dot product)
`get_charlbl.m`	get character labels, e.g. '(a)', '(b)', ... for figures.
`get_five.m`	generate random cubochoric misorientation and random boundary plane normal pairs
`get_knn.m`	k-nearest neighbor points, distances, mean, and std
`get_walltimefn.m`	get a function handle for computing interp5DOF SLURM walltimes (e.g. 'gpr')
`hexscatter.m`	A scatter-plot substitutegenerate a density plot using hexagonal patches.
`idw.m`	inverse-distance weighting interpolation
`idw_tovar.m`	Original inverse distance weight function by Andrew Tovar
`multiparity.m`	create tiled parity plots using cell parity data
`multixyplots.m`	create tiled xy-plots from variables in a table
`nnhist.m`	nearest neighbor distance histogram
`nnhist_test.m`	nnhist test
`padcat.m`	concatenate vectors with different lengths by padding with NaN
`paperfigure.m`	call figure in centimeters and with appropriate size
`papertext.m`	do a text() command for the figure labels '(a)', '(b)', etc. for num == 1, 2, etc.
`plotting.m`	plotting script for interp5DOF paper
`po2el.m`	convert polar angles to elevation angles
`qlab2qm.m`	Convert lab/sample frame quaternions of grain A and grain B and
`qmA2nA.m`	QLAB2FIVE Convert lab/sample frame quaternions of grain A and grain B and
`quivplot.m`	plot three quivers in the x-hat, y-hat, and z-hat directions
`savefigpng.m`	save a figure and print the figure as 300 DPI .png
`sphplot.m`	plot a simple sphere for visualization purposes
`tblfilt.m`	filter a table based on a struct of parameters (deprecated, see built-in findgroups() and splitapply())
`tblfilt_test.m`	parfilter_test
`test_voronoisphere.m`	Script to test voronoisphere (modified from original (Bruno Luong) by Sterling Baird)
`toBPFZ_test.m`
`vcell_solidangle.m`	Compute the solid angles of All voronoi cell
`voronoisphere.m`	Compute the voronoi's diagram of points on the spheres S^2
`xyplot.m`	make an errorbar xyplot using a table (tbl) and output (G) from findgroups()
`xyplots.m`	plot multiple datasets on the same axes using a "master" table and findgroups()

Advanced Installation

Basic steps:

Step 0: download the code
Step 1: set interp/ as working directory
Step 2: add subfolders to path (addpath(genpath('.'))) and run interp5DOF_test.m to verify it works

Platform-specific directions

Windows

Step 0: Download the code
Download GitHub Desktop and Git Bash. For Git Bash, the default installation options should be fine. I prefer to use Atom as the text editor which has some slick integrations with git. Login to GitHub Desktop and make a dummy repository via Ctrl+N so that you can open Git Bash via GitHub Desktop. Then clone and/or fork https://github.com/sgbaird-5DOF/interp.git by opening the Git Bash command line (i.e. Menubar --> Repository --> "Open in Git Bash") or

Ctrl+`

then run the following command in the directory where you want the interp directory to appear:

git clone --recurse-submodules https://github.com/sgbaird-5DOF/interp.git

Alternatively, you can try cloning directly in GitHub Desktop or via the "Open in GitHub Desktop" button under , but it will likely throw an error, and it may not correctly clone the MATslurm submodule by the time it reaches that error. MATslurm is a bare minimum requirement for running interp5DOF.m. Attempt at your own risk.

Step 1: open MATLAB and navigate to navigate to interp-5DOF/code/

matlab
cd interp-5DOF/code/

Step 2: Add subfolders to path and run interp5DOF_test.m

>> addpath(genpath('.'))

>> interp5DOF_test

Linux

Step 0: download the code

git --recurse-submodules https://github.com/sgbaird-5DOF/interp.git

Step 1: open MATLAB and navigate to navigate to interp-5DOF/code/
matlab

>> cd interp-5DOF/code/

Step 2: Add subfolders to path and run interp5DOF_test.m

>> addpath(genpath('.'))

>> interp5DOF_test

Troubleshooting

See cloning a repository and git submodules for more information or other options such as using GitHub Desktop (Windows, Linux, etc.) or downloading a .zip file. Forking, pull requests, and opening of issues are welcome/encouraged. Note that the .zip files will not contain submodules, which means that you'll need to download any submodules individually if you go that route (bare minimum would be the MATslurm repository). Instead of downloading a .zip file, I suggest instead downloading and using GitHub Desktop. If you run into issues with the repository, you can download a lightweight version of interp5DOF.m and its dependencies, unzip it, and read README.txt for instructions, but please open up an issue in the GitHub repo if you do run into trouble with the repo. That way, you can get the most recent updates and others can benefit from it.

Adding as Submodule

If you wish to add the interp repository as a submodule to your own repository, first navigate to where you would like the submodule to appear, and then run the following commands in git bash:

git submodule add https://github.com/sgbaird-5DOF/interp.git
git submodule update --init --recursive

Then commit/push your changes.

If you later need to remove the submodule from your repository (or need to start over), you will need to do the following:

Run git rm --cached <submodule name>
Delete the relevant lines from the .gitmodules file.
Delete the relevant section from .git/config.
Commit
Delete the now untracked submodule files.
Remove directory .git/modules/<submodule name> (Source)

Citing

Baird, S. G.; Homer, E. R.; Fullwood, D. T.; Johnson, O. K. Five Degree-of-Freedom Property Interpolation of Arbitrary Grain Boundaries via Voronoi Fundamental Zone Framework. Computational Materials Science 2021, 200, 110756. https://doi.org/10.1016/j.commatsci.2021.110756.

Baird, S. G.; Homer, E. R.; Fullwood, D. T.; Johnson, O. K. Towards a Quantitative Cartography of the Grain Boundary Energy Landscape: Paths and Correlations; preprint; Chemistry, 2021. https://doi.org/10.26434/chemrxiv-2021-ds0ml.

GB_octonion_code

Chesser, I., Francis, T., De Graef, M., & Holm, E. A. (2020). Learning the Grain Boundary Manifold: Tools for Visualizing and Fitting Grain Boundary Properties. Acta Materialia. https://doi.org/10.2139/ssrn.3460311

Francis, T., Chesser, I., Singh, S., Holm, E. A., & De Graef, M. (2019). A geodesic octonion metric for grain boundaries. Acta Materialia, 166, 135–147. https://doi.org/10.1016/j.actamat.2018.12.034

Name		Name	Last commit message	Last commit date
Latest commit History 2,441 Commits
.github/workflows		.github/workflows
code		code
data		data
parameters		parameters
results		results
.gitattributes		.gitattributes
.gitignore		.gitignore
.tokeignore		.tokeignore
Comparison.png		Comparison.png
LICENSE		LICENSE
README.md		README.md
_config.yml		_config.yml
oct50000.mat		oct50000.mat

Provide feedback

Saved searches

Use saved searches to filter your results more quickly

Repository files navigation

Five Degree-of-Freedom Grain Boundary Interpolation

Dependencies

MATLAB Version

R2007a - R2019a

MATLAB Toolboxes

Files

Getting Started

Quick Installation

Basic Usage

Simple Example Data

Test functions

Distance Calculations

Plots

Data Preparation

Active vs. Passive Rotation Convention

parfor loops

File dependencies

Contents.m (short descriptions)

Advanced Installation

Basic steps:

Platform-specific directions

Windows

Linux

Troubleshooting

Adding as Submodule

Citing

About

Releases 3

Packages

Contributors 4

Languages

License

sgbaird-5DOF/interp

Folders and files

Latest commit

History

Repository files navigation

Five Degree-of-Freedom Grain Boundary Interpolation

Dependencies

MATLAB Version

R2007a - R2019a

MATLAB Toolboxes

Files

Getting Started

Quick Installation

Basic Usage

Simple Example Data

Test functions

Distance Calculations

Plots

Data Preparation

Active vs. Passive Rotation Convention

parfor loops

File dependencies

Contents.m (short descriptions)

Advanced Installation

Basic steps:

Platform-specific directions

Windows

Linux

Troubleshooting

Adding as Submodule

Citing

About

Topics

Resources

License

Stars

Watchers

Forks

Releases 3

Packages 0

Contributors 4

Languages

Packages