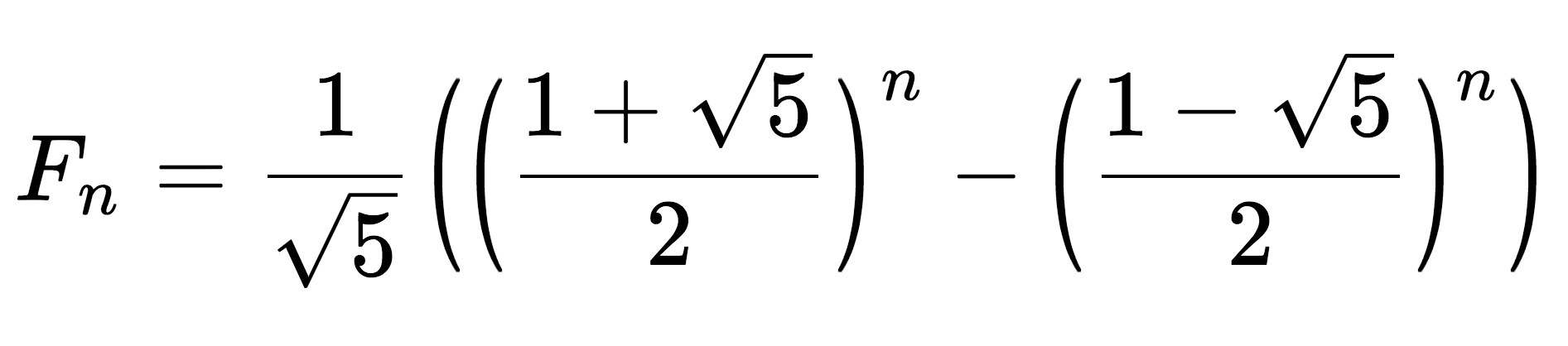Competative Programming = (Maths) + (Theoretical knowledge of algorithm design) + (Implementation with a good programming skill).
| Data Type | Bits | Value Range | or |
|---|---|---|---|
| int | 32 | -2x10^9 ... 2x10^9 | -2x10^31 ... 2x10^31 - 1 |
| long long (suffix ll) | 64 | -9x10^18 ... 9x10^18 | -2x10^63 ... 2x10^63 - 1 |
| double | 64 | -9x10^18 ... 9x10^18 | -2x10^63 ... 2x10^63 - 1 |
| long double | 80 | Accurate for absolute value > 2^53 | -2x10^79 ... 2x10^79 - 1 |
| __int128_t (g++) | 128 | -10^38 ... 10^38 | -2x10^127 ... 2x10^127 - 1 |

| Input size | Required time complexity : assuming a time limit of [1 second] |
|---|---|
| n <= 10 | O(n!) |
| n <= 20 | O(2^n) |
| n <= 500 | O(n^3) |
| n <= 5000 | O(n^2) |
| n <= 10^6 | O(nlogn) or O(n) |
| n is large | O(1) or O(logn) |
| Complexity Classes | Relation with input (n) |
|---|---|
| O(1) | The running time of a constant-time algorithm does not depend on the input size. |
| O(logn) | A logarithmic algorithm often halves the input size at each step.[Divided by the base] |
| O(sqrt(n)) | A square root algorithm is slower than O(logn) but faster than O(n). |
| O(n) | This is often the best possible time complexity, because it is usually necessary to access each input element at least once before reporting the answer. |
| O(nlogn) | This time complexity often indicates that the algorithm sorts the input. Another possibility is that the algorithm uses a data structure where each operation takes O(logn) time. |
| O(n^2) | A quadratic algorithm often contains two nested loops. |
| O(n^3) | A cubic algorithm often contains three nested loops. |
| O(2^n) | This time complexity often indicates that the algorithm iterates through all subsets of the input elements. |
| O(n!) | This time complexity often indicates that the algorithm iterates through all permutations of the input elements. |

- vector - Uses general arrays
- string - Is a vector
- set - Uses balanced binary tree [O(logn)]
- unordered_set - Uses hashing [O(1)]
- multiset - Allows multiple values in set, binary tree
- unordered_multiset - Allows multiple values, hashing
- indexed_set - POLICY BASED data structure, set with indexes [O(logn) Not present in STL]
- map - Uses balanced binary tree [O(logn)]
- unordered_map - Uses hashing [O(1)]
- bitset - Array of bits, require less memory
- stack - Can access only top element[O(1)]
- queue - Can add at last an remove from front[O(1)]
- deque - Vector with both fron and back push-pop, slower than vector
- priority_queue - min and max heap [insertion and removal takes O(logn) retrival take O(1)]
- Kadane’s algorithm
- Merge Sort
- Binary Search
// Binary Search template for implementation int k = 0; for (int b = n/2; b >= 1; b /= 2) { while (k+b < n && array[k+b] <= x) k += b; } if (array[k] == x) { // x found at index k }
- Huffman coding
- Memoization
- Bellman–Ford, SPFA algorithm
- Dijkstra’s algorithm
- Floyd–Warshall algorithm
- Kruskal’s algorithm with Union-find structure
- Prim’s algorithm
- Kosaraju’s algorithm
- C++ standard library functions based on binary search and work in logarithmic time:
• lower_bound(startpointer,endpointer,value) returns a pointer to the first array element whose value is at least x.
• upper_bound(startpointer,endpointer,value) returns a pointer to the first array element whose value is larger than x.
• equal_range(startpointer,endpointer,value) returns both above pointers.- The g++ compiler provides the following functions for counting bits:
The above functions only support int numbers, there are also long long versions of the functions available with the suffix ll.
• __builtin_clz(x): the number of zeros at the beginning of the number
• __builtin_ctz(x): the number of zeros at the end of the number
• __builtin_popcount(x): the number of ones in the number
• __builtin_parity(x): the parity (even or odd) of the number of ones- Modular Arithmetic
- Sum Formulas - Series : Faulhaber’s formula, AP, GP and Harmonic
- Set Theory
- Logic
- Functions
- Factorials
- Fibbonacci Numbers : Binet's Formula
- Logarithms
- Brute force: Getting Subsets and Permutations
- Backtracking and Pruning
- Meet in the middle search
- Greedy Algorithms
- Dynamic Programming
- Minimum/Maximum query: Sparse Table method
- Sum queries: Prefix Sum Algorithm, Difference array - Binary indexed tree: Fenwick tree
- Segment tree : Sum,Minimun,Maximum - Index compression
- Basics of a Graph and Tree : Keywords and Terms
- Representation : Adjacency list, Matrix, Edge list
- Traversal : Deapth-first Search - bipertiteness-cycles-connectivity check, Breadth-first Search [O(n+e)] | Preorder,Postorder,Inorder
- Directed Graph : Topological sort
- A property of logarithms is that the number of digits of an integer x in base b is [logb(x) + 1]
- A useful property of logarithms is that logk(x) equals the number of times we have to divide x by k before we reach the number 1
- The newline "\n" in c++ works faster than endl, because endl always causes a flush operation
- A time complexity is only an estimate of efficiency, because it hides the constant factors.
- NP-hard problems are an important set of problems, for which no polynomial algorithm is known
- A useful concept when analyzing sorting algorithms is an inversion: a pair of array elements (array[a],array[b]) such that a < b and array[a] > array[b], i.e., the elements are in the wrong order.
- Counting sort is a very efficient algorithm but it can only be used when the constant c is small enough, so that the array elements can be used as indices in the bookkeeping array.
- An important use for binary search is to find the position where the value of a function changes
- An iterator is a variable that points to an element in a data structure.
- If the value of a key is requested but the map does not contain it, the key is automatically added to the map with a default value.
- Heap structure is much simpler than a balanced binary tree.
- Bit representation of 25 is 11001, which corresponds to the subset {0,3,4}
- Using the and operation, we can check if a number x is even because x & 1 = 0 if x is even, and x & 1 = 1 if x is odd. More generally, x is divisible by 2^k exactly when x & (2^k-1) = 0.
- Note that x << k corresponds to multiplying x by 2^k, and x >> k corresponds to dividing x by 2^k rounded down to an integer.
- A number of the form 1 << k has a one bit in position k and all other bits are zero, so we can use such numbers to access single bits of numbers. In particular, the kth bit of a number is one exactly when x & (1 << k) is not zero.
- The formula x | (1 << k) sets the kth bit of x to one, the formula x & ~(1 << k) sets the kth bit of x to zero, and the formula x ^ (1 << k) inverts the kth bit of x.
- The formula x & (x-1) sets the last one bit of x to zero, and the formula x &-x sets all the one bits to zero, except for the last one bit. The formula x | (x-1) inverts all the bits after the last one bit.
- A positive number x is a power of two exactly when x & (x-1) = 0.
- It is difficult to find out if the nodes in a graph can be colored using k colors so that no adjacent nodes have the same color. Even when k = 3, no efficient algorithm is known but the problem is NP-hard
 ShankarLohar |
|---|
https://cses.fi/book/book.pdf