-
Notifications
You must be signed in to change notification settings - Fork 130
Graph model
Reactive programming is a declarative paradigm. The programmer defines how to calculate something, but the control flow to run these calculations is implicitly handled by a runtime engine.
The dependency relations between reactive values form a graph which models the dataflow.
Each reactive value is a node and edges denote dependency relations.
If an edge exists from a to b that means a will propagate its changes to b.
In other words, after a node changed, all its successors will be updated.
To give an example, let a, b and c be arbitrary reactive values.
x is another reactive value that combines the former through use a binary operation +, which can be applied to reactive operands:
x = (a + b) + c;This is the matching dataflow graph:

The graph data structures are not directly exposed by the API; they are accessible through lightweight proxies instead. Such a proxy is essentially a shared pointer to the heap-allocated node. The concrete type of the node is hidden behind the proxy.
One observation made from the previous example is that not all nodes in the graph are bound to a proxy; the temporary sub-expression a + b results in a node as well.
If a new node is created, it takes shared ownership of its dependencies, because it needs them to calculate its own value. This prevents the a + b node from disappearing.
The resulting reference graph is similar to the dataflow graph, but with reverse edges (and as such, a DAG as well):
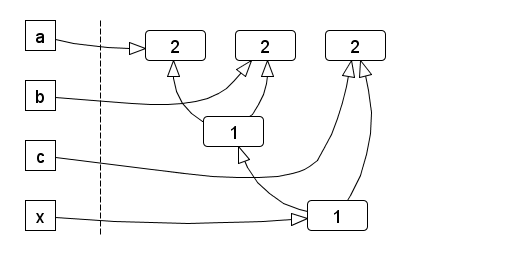
The number inside each node denotes its reference count. On the left are the proxy instances exposed by the API.
Assuming the handles for a, b and c would go out of scope but x remains, the reference count of all nodes is still 1, until x disappears as well.
Once that happens, the graph is deconstructed from the bottom up.
As stated before, a reactive graph is not constructed explicitly, but rather a result of declaring reactives and their dependencies.
It is generally not possible to construct cyclic graphs. Attempting to do so as shown in the following example will result in an error:
SignalT<U> a;
SignalT<U> b;
a = MakeSignal(b, ...);
b = MakeSignal(a, ...);b is still invalid at the time of construction, because it's not linked to any node. As such, the code will compile, but fail a runtime assertion.
The exception to this rule are higher order reactives:
VarSignalT<U> in = MakeVar<D>(...);
VarSignalT<SignalT<U>> outer = MakeVar<D>(a);
SignalT<U> flat = Flatten(outer);
// Cycle
outer <<= flat;Creating cyclic graphs results in undefined behaviour.
A closed, self-contained reactive system would ultimately be useless, because there's no way to get information in or out. In other words, we need to be able to
- react to changes from the outside world;
- propagate effects to the outside world.
The outside world here just means the larger context of the program the reactive system is part of.
To address the first requirement, we introduce designated input nodes at the root of the graph.
They are the input interface of the reactive system and can be manipulated imperatively.
This allows straightforward integration of a reactive system with an imperative program.
At first glance, propagating changes to the outside world doesn't appear to be a problem.
Reactive values are often declared in terms of functions that calculate their values, so inside these functions we could apply side-effects (i.e. output).
The problem is that this violates functional purity.
Consequently, it can no longer be assumed that its safe to execute a function with side-effects in parallel or that the number of times it is executed is irrelevant.
To avoid this, we move all side-effects to designated output nodes, whose sole purpose is to cause the former.
By definition, these nodes don't have any successors. Analogously to input nodes, they are the output interface of the reactive system.
Having a closed reactive system with well-defined interfaces is a first step towards designing a modular components, but having a single reactive system is