-
-
Notifications
You must be signed in to change notification settings - Fork 188
OpenCL Kernels
This is where you'll find information on the non-trivial OpenCL kernels. This documentation serves as a complement to the code documentation and holds the images that are linked in the code comments.
The basic idea for the inverse calculation is explained here or in the report.
If we calculate lower triangular inverses of A1 and A2 to get C1 and C2, we can calculate the remaining C3 submatrix by calculating C3 = -C2*A3*C1. In Short:
-
diag_inv: CalculateC1andC2. -
inv_lower_tri_multiply: Calculatestemp = C2*A3and -
neg_rect_lower_tri_multiplyCalculates-temp*C1.
This wiki is a work in progress. If you have suggestions or feel that any of the other OpenCL kernels need additional explanation, please mention it on our forums on.
This document serves as a guide for explaining the batch algorithms for lower triangular matrix inversion on the GPU. See this paper for more details than what is explained below. The kernels are required for efficient computation of Cholesky decompositions on the GPU, which are used in a variety of Stan models (especially Gaussian Processes). The most efficient algorithm for Cholesky decomposition (with gradients) on the GPU involves breaking the target matrix up into several lower triangular blocks, all of which need have the inverses calculated for them.
This is what the recursive structure looks like:
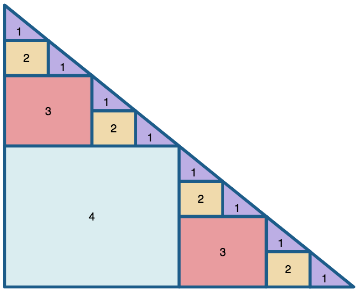
Several kernels are used to break the subdivision into “parts” (as written in the code) easier, and allows us to take the inverses. There are 3 steps and a helper kernel called “batch_identity,” up first.
A is the input matrix and tmp_inv is the output of the batch_identity kernel. After the kernel is executed the input matrix A has lower triangular inverses calculated on submatrices on the diagonal: [0:TB, 0:TB], [TB:2*TB, TB:2*TB], [2*TB:3*TB, 2*TB:3*TB], ... where TB is the size of the thread block.
If TB is equal or larger than the input matrix A, the result of this kernel is the complete lower triangular inverse of A.
More often, TB is smaller than A. In that case this kernel calculates the inverse on the smaller blocks of A across the diagonal. An example of such an instance is given in the image below. diag_inv calculates the inverse in the blue colored triangles on the diagonal.
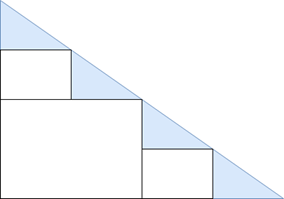
This kernel is run with threads organized in a single dimension. If we want to calculate N blocks of size TB across the diagonal we spawn N x TB threads with TB used as the thread block size. We therefore have N blocks of threads.
neg_rect_lower_tri_multiply(__global double* A, __global double* temp, const int A_rows, const int rows)
inv_lower_tri_multiply and neg_rect_lower_tri_multiply are special cases of matrix multiplication. The differences of these 2 kernels compared to the multiply() kernel:
- multiplying submatrices in the input matrix A
- multiple matrix multiplications in parallel
- optimizations due to lower triangular input (sub)matrices
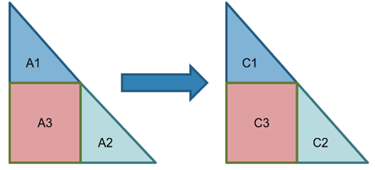
This is the simplest case for these steps. Generally, diag_inv computes more a larger number of inverses. For the example below, inverse_lower_tri_multiply and neg_rect_lower_tri_multiply are repeated 3 times. First to calculate the four submatrices labeled with 2 in parallel, then the two submatrices labeled with 3 and finally calculate the submatrix labeled with 4.

Both kernels are executed using (N, N, m) threads, where N is the size of the input matrices (size of submatrices labeled 1 when calculating submatrices labeled with 2; size of submatrices 1 and 2 when calculating submatrices labeled with 3;...). m is the number of results that we need to calculate (4, 2 and 1 in the above case).
Step 2 code ( code that is the same as in the multiply() kernel is omitted):
The code is explained in the below case, where we want to calculate 2 blue submatrices.
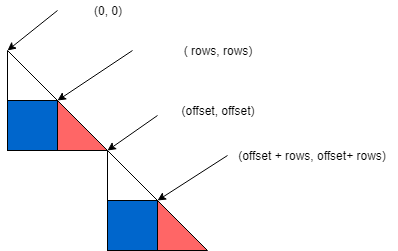
// The ID of the resulting matrix.
int result_matrix_id = get_global_id(2);
// Calculate offset, which is ID* rows *2 (see image above).
int offset = result_matrix_id * rows * 2;
const int thread_block_row = get_local_id(0);
const int thread_block_col = get_local_id(1);
result_matrix_id and the global thread row and column are used to assign the matrix element the thread will calculate. The first assigns which of the blue submatrices is selected, while row and column determine which element inside the submatrix will be calculated in the thread.
const int global_thread_row
= THREAD_BLOCK_SIZE * get_group_id(0) + thread_block_row;
const int global_thread_col
= THREAD_BLOCK_SIZE * get_group_id(1) + thread_block_col;
When transferring data to the local memory, each thread transfers 1 element. Threads that are assigned elements above the diagonal assign zeros to avoid unnecessary global memory accesses. The C2_global_col and row determines the element in the red triangle that the thread will transfer to the local memory. The same is
const int C2_global_col
= offset + rows + tiled_j + w * THREAD_BLOCK_SIZE_COL;
const int C2_global_row = offset + global_thread_row + rows;
const int A3_global_col
= offset + global_thread_col + w * THREAD_BLOCK_SIZE_COL;
const int A3_global_row = tiled_i + rows + offset;
The local ids determine which memory location in the local memory the threads transfer the values from the global memory for both submatrices.
const int local_col = thread_block_col + w * THREAD_BLOCK_SIZE_COL;
const int local_row = thread_block_row;
// Element above the diagonal will not be transferred.
if (C2_global_col <= C2_global_row) {
C2_local[local_col][local_row]
= A[C2_global_col * A_rows + C2_global_row];
} else {
C2_local[local_col][local_row] = 0;
}
A3_local[local_col][local_row]
= A[A3_global_col * A_rows + A3_global_row];
Finally, the result is stored in a temporary matrix that stores all resulting submatrices in a contiguous memory space.
batch_offset is the global offset for each resulting submatrix. the temp_global_row and temp_global_col determine the element inside the submatrix
const int batch_offset = result_matrix_id * rows * rows;
const int temp_global_row = global_thread_row;
for (int w = 0; w < WORK_PER_THREAD; w++) {
// each thread saves WORK_PER_THREAD values
const int temp_global_col
= global_thread_col + w * THREAD_BLOCK_SIZE_COL;
temp[batch_offset + temp_global_col * rows + temp_global_row] =
acc[w];
}
In the step 3 kernel, the ideas are the same. The only difference is that one of the input submatrices is retrieved from temp and the results are stored in the matrix A.
Home | Users | Developers