-
Notifications
You must be signed in to change notification settings - Fork 14
exam_12
- Архипов С.С.
- Абрамов А.С.
1. Диаграммы Исикавы, их назначение и возможности применения при объектно-ориентированном подходе к анализу и проектированию.
Диаграмма Исикавы, или диаграмма «рыбьей кости» (англ. Fishbone Diagram), или причинно-следственная диаграмма (англ. Cause and Effect Diagram), или диаграмма анализа корневых причин — один из основных инструментов измерения, оценивания, контроля и улучшения качества производственных процессов.
Диаграмма Исикавы — графический способ исследования и определения наиболее существенных причинно-следственных взаимосвязей между факторами и последствиями в исследуемой ситуации или проблеме.
Такая диаграмма позволяет выявить ключевые взаимосвязи между различными факторами и более точно понять исследуемый процесс. Диаграмма способствует определению главных факторов, оказывающих наиболее значительное влияние на развитие рассматриваемой проблемы, а также предупреждению или устранению действия данных факторов.
Схема находит широкое применение при разработке новой продукции, с целью выявления потенциальных факторов, действие которых вызывает общий эффект.
Вид диаграммы при рассмотрении поля исследуемой проблемы действительно напоминает скелет рыбы (глаза обычно движутся слева направо, как при чтении строки текста). Проблема обозначается основной стрелкой. Факторы, которые усугубляют проблему, отражают стрелками, покосившимися к основной вправо, а те, которые нейтрализуют проблему — с наклоном влево. При углублении уровня анализа к стрелкам факторов могут быть добавлены стрелки влияющих на них факторов второго порядка и т. д. (Рис. 1)
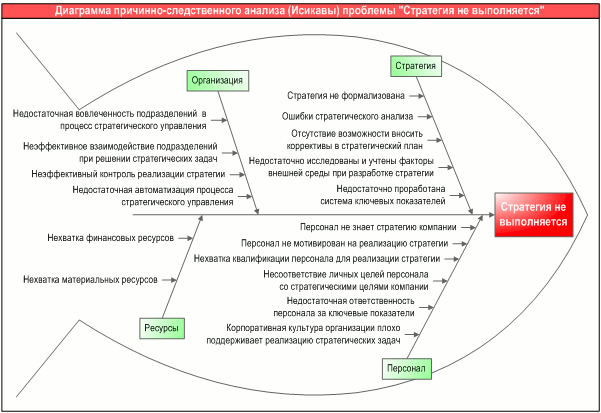
Рис.1 Общий вид диаграммы Исикавы
Диаграмма Исикавы имеет преимущества:
- помогает наглядно показать связи между полученным результатом и вызвавшими его причинами;
- позволяет провести анализ цепочки факторов, воздействующих на проблему[8].
Первый шаг. Необходимо максимально четко определить предмет изучения или проблему, лаконично описать её и записать формулировку на рабочее поле в прямоугольнике с правой или левой стороны. От прямоугольника влево (вправо) нужно провести прямую горизонтальную линию(Рис.2).

Рис.2 Метод построения диаграммы Исикавы — проблема и категории
Второй шаг. Над горизонтальной линией и под ней указываются группы факторов, влияющих на результат. Обычно в список групп входят так называемые «люди», «методы», «механизмы», «материалы», «контроль» и «среда»(Рис.3).

Рис.3 Диаграмма Исикава категории и причины
«люди» — группа причин, обусловленных состоянием и возможностями человека, то есть влиянием человеческого фактора.
Например — уровень опыта, физические кондиции, способности, мотивация, состояние здоровья и прочие;
«методы» — группа причин, обусловленных тем, каким образом делается работа, также сюда включают всё, что относится к точности или производительности отдельных операций процесса или его стадий;
«механизмы» — группа причин, связанных с используемым оборудованием, оснасткой, которые использованы в процессе; например, наличие и состояние рабочего и измерительного инструмента, применение каких-то дополнительных устройств;
«материалы» включает в себя факторы, определяющие измеримые параметры и качества материала, участвующего в процессе; Например, температура, состав, упругость, влажность, вязкость или твердость;
«контроль» включает в себя обстоятельства, влияющие на надежное и своевременное обнаружение ошибочных действий;
«среда» — группа, включающая все значимые условия, обусловленные внешней средой и влияющие на процесс и результат действий; например, давление, температура воздуха, воды, степень освещенности;
Необязательно использовать в рамках одного исследования все категории сразу, но нежелательно ограничиваться одной или двумя. Нужно исходить из соображений разумной достаточности[1].
Третий шаг. Выбранные категории вписываются в прямоугольники, от них проводятся наклонные линии к уже имеющейся горизонтали(Рис.4).

Рис.4 Распределение причин по группам-категориям
Четвертый шаг. Причины изучаемой проблемы или действующие факторы распределяются по установленным категориям («люди», «механизмы» и т. д.) и указываются на диаграмме в виде линий, примыкающих к линиям категорий.
Пятый шаг. Необходимо разложить каждую из причин на составляющие. Для этого по поводу каждой причины нужно задать себе вопрос – «В связи с чем это случилось?»
Ответы нужно фиксировать в виде ветвей более низкого уровня. Детализация причин должна продолжаться до тех пор, пока не будет найдена «корневая» причина.
Второстепенные причины в диаграмме Исикавы
Примечание. В некоторых источниках рекомендуется выделять факторы, позитивно влияющие на результат и негативные факторы. С этой целью линии, обозначающие их связь с категорией, проводят в разных направлениях, например, «позитив» налево либо изнутри от осевой линии, «негатив» — направо либо снаружи к оси — как на рисунке. Это непринципиально, можно делать так как удобно, выделять факторы цветом линий или не выделять их вообще.
Шестой шаг. Из числа первопричин выделяются наиболее значимые факторы, которые влияют на изучаемую проблему(Рис.5).

Рис.5 Диаграмма Исикавы позитивные и негативные факторы
2. Равномерное, нормальное и экспоненциальное распределения, типовые приемы и способы их применения в задачах имитационного моделирования.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их появления.
Имитационное моделирование — метод исследования, при котором изучаемая система заменяется моделью, с достаточной точностью описывающей реальную интересующую систему, с которой проводятся эксперименты с целью получения информации об этой системе. Такую модель можно «проиграть» во времени интересующее количество раз[8]. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.
Равномерное распределение, также известное как прямоугольное - распределение, в котором значения случайной величины с двух сторон ограничены отрезком [a,b] и в границах интервала имеют одинаковую вероятность. Это означает, что в в данном интервале плотность вероятности постоянна[2]. Плотность вероятности задаётся законом
Равномерное распределение бывает двух типов - дискретное и непрерывное.
Дискретное
- a и b принадлежат к целым числам;
- n - число значений в распределении, оно конечно и его можно представить как b-a.
- Пример: подбрасывание монеты, бросок игральной кости[7].
- График плотности вероятностей представлен на рисунке 1.

Рис. 1. График плотности вероятностей для дискретной случайной величины
Непрерывное
- a и b принадлежат к действительным числам
- Значения f(x) в крайних точках a и b участка (a, b) не указываются, так как вероятность попадания в любую из этих точек для непрерывной случайной величины равна нулю.
- Способы генерации чисел:
- Аппаратный - числа формируются специальным внешним устройством;
- Табличный - случайные числа в виде таблицы из достоверного источника;
- Алгоритмический - формирование случайных чисел при помощи программно реализованных алгоритмов.
- Равномерным распределением часто моделируют время ожидания транспорта, ошибки округления в пределах цены деления.
- График плотности вероятностей представлен на рисунке 2.

Рис. 2. График плотности вероятностей для непрерывной случайной величины
Нормальное распределение, также известное как распределение Гаусса или распределение Гаусса-Лапласа - распределение вероятностей, для одномерного варианта плотность вероятности которого задаётся законом 
- μ - значение математического ожидания, среднее значение, медиана, мода:
- Может принимать значения от -∞ до +∞;
- При изменении кривая сдвигается вдоль оси х.
- σ - значение среднеквадратичного отклонения, стандартное отклонение/разброс (σ² — дисперсия):
- Может принимать значения от 0 до ∞;
- При увеличении параметра кривая растекается вдоль оси х, при стремлении к 0 сжимается вокруг среднего значения, так как параметр характеризует разброс, рассеяние[7].
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием(μ) 0 и стандартным отклонением(σ) 1.

Рис. 3 График плотности вероятностей
Играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех, такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий. Типичное применение нормального закона в анализе, например, телекоммуникационных данных – моделирование сигналов, описание шумов, помех, ошибок, трафика[3].
Экспоненциальное распределение - распределение вероятностей, подчиняющееся закону распределения 

Рис. 4. Плотность вероятностей экспоненциального распределения
Области применения:
- Задачи в теории массового обслуживания, экспоненциальное распределение описывает распределение наработки на отказ сложных изделий, время безотказной работы элементов радиоэлектронной аппаратуры. X - например, время ожидания при техническом обслуживании;
- Задачи в теории надежности, часто используют для прогнозирования надежности в период нормальной эксплуатации изделий, когда постепенные отказы еще не проявились и надежность характеризуется внезапными отказами. Здесь X - например, срок службы радиоэлектронной аппаратуры[6].
Взаимосвязь между первым и вторым вопросами можно наблюдать в объектно-ориентированном подходе на этапе анализа и/или проектирования при построении моделей. Т.е. модель строится в виде диаграммы Исикавы, а позитивные и негативные факторы на "ребрах" модели оцениваются с помощью равномерного, нормального или экспоненциального распределения.
- Диаграммы Исикавы и ее применение [Электронный ресурс] - http://point-v.ru/stati/diagramma-isikavyi.html, (дата обращения 12.05.2019).
- Равномерное распределение [Электронный ресурс] - http://statistica.ru/theory/ravnomernoe-raspredelenie/, (дата обращения 12.05.2019).
- Нормальное распределение [Электронный ресурс] - http://www.machinelearning.ru/wiki/index.php?title=Нормальное_распределение#.D0.A1.D0.B2.D0.BE.D0.B9.D1.81.D1.82.D0.B2.D0.B0, (дата обращения 12.05.2019).
- Экспоненциальное распределение и его свойства [Электронный ресурс] - http://statistica.ru/theory/eksponentsialnoe-raspredelenie/, (дата обращения 12.05.2019).
- Экспоненциально распределенная случайная величина [Электронный ресурс] - https://www.matburo.ru/ex_tv.php?p1=tvexp, (дата обращения 12.05.2019).
- Надежность технических систем и техногенный риск: учебное пособие [Электронный ресурс] - http://window.edu.ru/catalog/pdf2txt/883/36883/13896?p_page=2, (дата обращения 12.05.2019).
- Закон распределения случайных величин. Нормальное распределение. Показательное распределение. Равномерное распределение. Некоторые другие виды распределения. [Электронный ресурс] - https://studfiles.net/preview/996709/page:7/, (дата обращения 12.05.2019).
- Википедия - свободная энциклопедия [Электронный ресурс] - https://ru.wikipedia.org/wiki/, (дата обращения 12.05.2019).
