CamTools: Camera Tools for Computer Vision

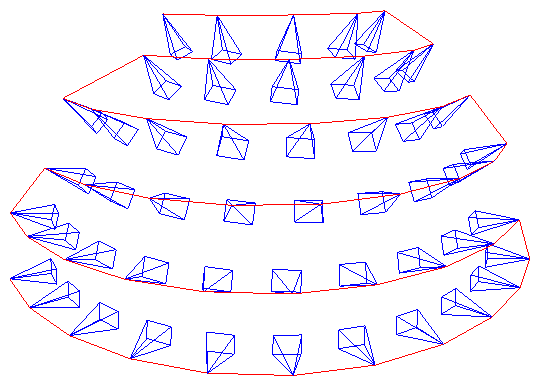
CamTools is a collection of tools for handling cameras in computer vision. It can be used for plotting, converting, projecting, ray casting, and doing more with camera parameters. It follows the standard camera coordinate system with clear and easy-to-use APIs.

What can you do with CamTools?

1. Plot cameras. Useful for debugging 3D reconstruction and NeRFs!

   import camtools as ct
   import open3d as o3d
   cameras = ct.camera.create_camera_frustums(Ks, Ts)
   o3d.visualization.draw_geometries([cameras])

   

2. Convert camera parameters.

   pose = ct.convert.T_to_pose(T)     # Convert T to pose
   T    = ct.convert.pose_to_T(pose)  # Convert pose to T
   R, t = ct.convert.T_to_R_t(T)      # Convert T to R and t
   C    = ct.convert.pose_to_C(pose)  # Convert pose to camera center
   K, T = ct.convert.P_to_K_T(P)      # Decompose projection matrix P to K and T
                                      # And more...

3. Projection and ray casting.

   # Project 3D points to pixels.
   pixels = ct.project.points_to_pixel(points, K, T)
   
   # Back-project depth image to 3D points.
   points = ct.project.im_depth_to_points(im_depth, K, T)
   
   # Ray cast a triangle mesh to depth image given the camera parameters.
   im_depth = ct.raycast.mesh_to_im_depth(mesh, K, T, height, width)
   
   # And more...

4. Image and depth I/O with no surprises.

   Strict type checks and range checks are enforced. The image and depth I/O APIs are specifically designed to solve the following pain points:

   • Is my image of type float32 or uint8?
   • Does it have range [0, 1] or [0, 255]?
   • Is it RGB or BGR?
   • Does my image have an alpha channel?
   • When saving depth image as integer-based .png, is it correctly scaled?

   ct.io.imread()
   ct.io.imwrite()
   ct.io.imread_detph()
   ct.io.imwrite_depth()

5. Command-line tools ct (runs in terminal).

   # Crop image boarders.
   ct crop-boarders *.png --pad_pixel 10 --skip_cropped --same_crop
   
   # Draw synchronized bounding boxes interactively.
   ct draw-bboxes path/to/a.png path/to/b.png
   
   # For more command-line tools.
   ct --help

   

6. And more.

   • Solve line intersections.
   • COLMAP tools.
   • Points normalization.
   • ...

Installation

To install CamTools, simply do:

pip install camtools

Alternatively, you can install CamTools from source with one of the following methods:

git clone https://github.com/yxlao/camtools.git
cd camtools

# Installation mode, if you want to use camtools only.
pip install .

# Editable mode, if you want to modify camtools on the fly.
pip install -e .

# Editable mode and dev dependencies.
pip install -e .[dev]

# Help VSCode resolve imports when installed with editable mode.
# https://stackoverflow.com/a/76897706/1255535
pip install -e .[dev] --config-settings editable_mode=strict

# Enable torch-related features (e.g. computing image metrics)
pip install camtools[torch]

# Enable torch-related features in editable mode
pip install -e .[torch]

Camera coordinate system

A homogeneous point [X, Y, Z, 1] in the world coordinate can be projected to a homogeneous point [x, y, 1] in the image (pixel) coordinate using the following equation:

$$ \lambda \left[\begin{array}{l} x \\ y \\ 1 \end{array}\right]=\left[\begin{array}{ccc} f_{x} & 0 & c_{x} \\ 0 & f_{y} & c_{y} \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{llll} R_{00} & R_{01} & R_{02} & t_{0} \\ R_{10} & R_{11} & R_{12} & t_{1} \\ R_{20} & R_{21} & R_{22} & t_{2} \end{array}\right]\left[\begin{array}{c} X \\ Y \\ Z \\ 1 \end{array}\right]. $$

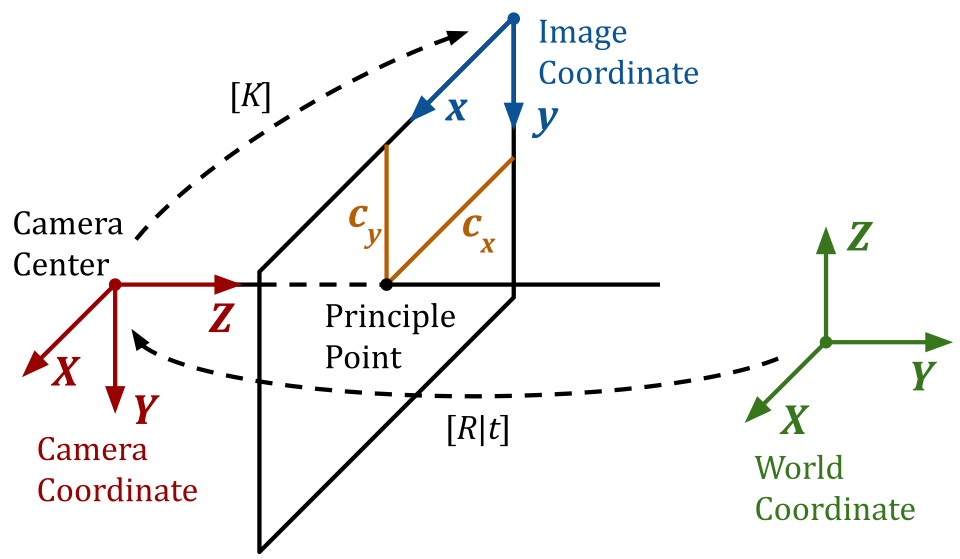
We follow the standard OpenCV-style camera coordinate system as illustrated at the beginning of the README.

• Camera coordinate: right-handed, with $Z$ pointing away from the camera towards the view direction and $Y$ axis pointing down. Note that the OpenCV convention (camtools' default) is different from the OpenGL/Blender convention, where $Z$ points towards the opposite view direction, $Y$ points up and $X$ points right. To convert between the OpenCV camera coordinates and the OpenGL-style coordinates, use the conversion functions:
  • ct.convert.T_opencv_to_opengl()
  • ct.convert.T_opengl_to_opencv()
  • ct.convert.pose_opencv_to_opengl()
  • ct.convert.pose_opengl_to_opencv()
• Image coordinate: starts from the top-left corner of the image, with $x$ pointing right (corresponding to the image width) and $y$ pointing down (corresponding to the image height). This is consistent with OpenCV. Pay attention that the 0th dimension in the image array is the height (i.e., $y$) and the 1st dimension is the width (i.e., $x$). That is:
  • $x$ <=> $u$ <=> width <=> column <=> the 1st dimension
  • $y$ <=> $v$ <=> height <=> row <=> the 0th dimension
• K: (3, 3) camera intrinsic matrix.

  K = [[fx,  s, cx],
       [ 0, fy, cy],
       [ 0,  0,  1]]

• T or W2C: (4, 4) camera extrinsic matrix.

  T = [[R  | t   = [[R00, R01, R02, t0],
        0  | 1]]    [R10, R11, R12, t1],
                    [R20, R21, R22, t2],
                    [  0,   0,   0,  1]]

  • T is also known as the world-to-camera W2C matrix, which transforms a point in the world coordinate to the camera coordinate.
  • T's shape is (4, 4), not (3, 4).
  • T is the inverse of pose, i.e., np.linalg.inv(T) == pose.
  • The camera center C in world coordinate is projected to [0, 0, 0, 1] in camera coordinate.
• R: (3, 3) rotation matrix.

  R = T[:3, :3]

  • R is a rotation matrix. It is an orthogonal matrix with determinant 1, as rotations preserve volume and orientation.
    • R.T == np.linalg.inv(R)
    • np.linalg.norm(R @ x) == np.linalg.norm(x), where x is a (3,) vector.
• t: (3,) translation vector.

  t = T[:3, 3]

  • t's shape is (3,), not (3, 1).
• pose or C2W: (4, 4) camera pose matrix. It is the inverse of T.
  • pose is also known as the camera-to-world C2W matrix, which transforms a point in the camera coordinate to the world coordinate.
  • pose is the inverse of T, i.e., pose == np.linalg.inv(T).
• C: camera center.

  C = pose[:3, 3]

  • C's shape is (3,), not (3, 1).
  • C is the camera center in world coordinate. It is also the translation vector of pose.
• P: (3, 4) the camera projection matrix.
  • P is the world-to-pixel projection matrix, which projects a point in the homogeneous world coordinate to the homogeneous pixel coordinate.
  • P is the product of the intrinsic and extrinsic parameters.

    # P = K @ [R | t]
    P = K @ np.hstack([R, t[:, None]])

  • P's shape is (3, 4), not (4, 4).
  • It is possible to decompose P into intrinsic and extrinsic matrices by QR decomposition.
  • Don't confuse P with pose. Don't confuse P with T.
• For more details, please refer to the following blog posts: part 1, part 2, and part 3.

Contributing

• Follow Angular's commit message convention for PRs.
  • This applies to PR's title and ultimately the commit messages in main.
  • The prefix shall be one of build, ci, docs, feat, fix, perf, refactor, test.
  • Use lowercase.
• Format your code with black. This will be enforced by the CI.

Build with CamTools

If you use CamTools in your project, consider adding one of the following badges to your project.