On the Versatile Uses of Partial Distance Correlation in Deep Learning - Official PyTorch Implementation

On the Versatile Uses of Partial Distance Correlation in Deep Learning
Xingjian Zhen, Zihang Meng, Rudrasis Chakraborty, Vikas Singh European Conference on Computer Vision (ECCV), 2022.

Update:

• Fixed typo in Partial_Distance_Correlation.ipynb from Peasor_Correlation() to Pearson_Correlation()
• Reimplementation in TensorFlow in TF_Partial_Distance_Correlation.ipynb
• Reimplementation in TF_Diverge_Training module

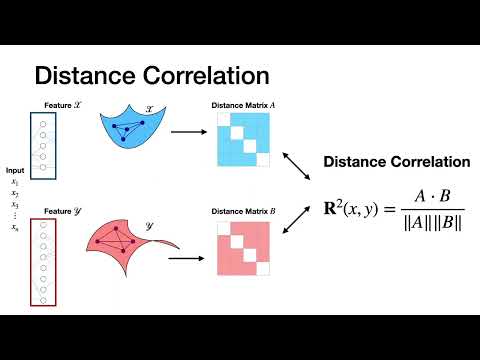
Abstract: Comparing the functional behavior of neural network models, whether it is a single network over time or two (or more networks) during or post-training, is an essential step in understanding what they are learning (and what they are not), and for identifying strategies for regularization or efficiency improvements. Despite recent progress, e.g., comparing vision transformers to CNNs, systematic comparison of function, especially across different networks, remains difficult and is often carried out layer by layer. Approaches such as canonical correlation analysis (CCA) are applicable in principle, but have been sparingly used so far. In this paper, we revisit a (less widely known) from statistics, called distance correlation (and its partial variant), designed to evaluate correlation between feature spaces of different dimensions. We describe the steps necessary to carry out its deployment for large scale models -- this opens the door to a surprising array of applications ranging from conditioning one deep model w.r.t. another, learning disentangled representations as well as optimizing diverse models that would directly be more robust to adversarial attacks. Our experiments suggest a versatile regularizer (or constraint) with many advantages, which avoids some of the common difficulties one faces in such analyses.

Please also go check the project webpage

Results

Independent Features Help Robustness (Diverge Training)

Table 1: The test accuracy (%) of a model $f_2$ on the adversarial examples generated using $f_1$ with the same architecture. "Baseline": train without constraint. "Ours": $f_2$ is independent to $f_1$. "Clean": test accuracy without adversarial examples.

Dataset	Network	Method	Clean	FGM $\epsilon=0.03$	PGD $\epsilon=0.03$	FGM $\epsilon=0.05$	PGD $\epsilon=0.05$	FGM $\epsilon=0.10$	PGD $\epsilon=0.10$
CIFAR10	Resnet 18	Baseline	89.14	72.10	66.34	62.00	49.42	48.23	27.41
CIFAR10	Resnet 18	Ours	87.61	74.76	72.85	65.56	59.33	50.24	36.11
ImageNet	Mobilenet-v3-small	Baseline	47.16	29.64	30.00	23.52	24.81	13.90	17.15
ImageNet	Mobilenet-v3-small	Ours	42.34	34.47	36.98	29.53	33.77	19.53	28.04
ImageNet	Efficientnet-B0	Baseline	57.85	26.72	28.22	18.96	19.45	12.04	11.17
ImageNet	Efficientnet-B0	Ours	55.82	30.42	35.99	22.05	27.56	14.16	17.62
ImageNet	Resnet 34	Baseline	64.01	52.62	56.61	45.45	51.11	33.75	41.70
ImageNet	Resnet 34	Ours	63.77	53.19	57.18	46.50	52.28	35.00	43.35
ImageNet	Resnet 152	Baseline	66.88	56.56	59.19	50.61	53.49	40.50	44.49
ImageNet	Resnet 152	Ours	68.04	58.34	61.33	52.59	56.05	42.61	47.17

Informative Comparisons between Networks (Partial Distance Correlation)

Table 2: Partial DC between the network $\Theta_X$ conditioned on the network $\Theta_Y$ , and the ImageNet class name embedding. The higher value indicates the more information.

Network $\Theta_X$	Network $\Theta_Y$	$\mathcal{R}^2(X, GT)$	$\mathcal{R}^2(Y, GT)$	$\mathcal{R}^2(X|Y, GT)$	$\mathcal{R}^2((Y|X), GT)$
ViT$^1$	Resnet 18$^2$	0.042	0.025	0.035	0.007
ViT	Resnet 50$^3$	0.043	0.036	0.028	0.017
ViT	Resnet 152$^4$	0.044	0.020	0.040	0.009
ViT	VGG 19 BN$^5$	0.042	0.037	0.026	0.015
ViT	Densenet121$^6$	0.043	0.026	0.035	0.007
ViT large$^7$	Resnet 18	0.046	0.027	0.038	0.007
ViT large	Resnet 50	0.046	0.037	0.031	0.016
ViT large	Resnet 152	0.046	0.021	0.042	0.010
ViT large	ViT	0.045	0.043	0.019	0.013
ViT+Resnet 50$^8$	Resnet 18	0.044	0.024	0.037	0.005
Resnet 152	Resnet 18	0.019	0.025	0.013	0.020
Resnet 152	Resnet 50	0.021	0.037	0.003	0.030
Resnet 50	Resnet 18	0.036	0.025	0.027	0.008
Resnet 50	VGG 19 BN	0.036	0.036	0.020	0.019

Note Accuracy: 1. 84.40%; 2. 69.76%; 3. 79.02%; 4. 82.54%; 5. 74.22%; 6. 75.57%; 7. 85.68%; 8. 84.13%

Disentanglement

Visualization

Quantitive measurement (distance correlation between residual and attribute of interest)

Table 3: DC between residual attributes (R) and attributes of interest, if we use the ground truth CLIP labeled data to measure the attribute of interest. Range from 0 to 1, and smaller is better.

age vs R.	gender vs R.	ethnicity vs R.	hair color vs R.	beard vs R.	glasses vs R
0.0329	0.0180	0.0222	0.0242	0.0219	0.0255

Table 4: DC between residual attributes (R) and attributes of interest, if we use in-model classifier to classify the attribute of interest. Range from 0 to 1, and smaller is better.

age vs R.	gender vs R.	ethnicity vs R.	hair color vs R.	beard vs R.	glasses vs R
0.0430	0.0124	0.0376	0.0259	0.0490	0.0188

Requirements

Training

Please refer to each different directory for detailed training steps for each experiment.

Citation

@inproceedings{zhen2022versatile,
  author    = {Zhen, Xingjian and Meng, Zihang and Chakraborty, Rudrasis and Singh, Vikas},
  title     = {On the Versatile Uses of Partial Distance Correlation in Deep Learning},
  booktitle = {Proceedings of the European conference on computer vision (ECCV)},
  year      = {2022}
}

If you use distance correlation for disentanglement, please give credit to the following paper: Measuring the Biases and Effectiveness of Content-Style Disentanglement which discusses a nice demonstration of distance correlation helps content style disentanglement. We were not aware of this paper when we wrote the paper last year and thank Sotirios Tsaftaris for communicating his findings with us.