-
Notifications
You must be signed in to change notification settings - Fork 558
System Introduction
Graph is a generic data structure with strong expressivity to characterize entities and their interactions in real world, and have beed employed extensively in various areas, such as the friend network in social area, the user and item network in e-commerce area, the communication network in telecommunication area, the transaction network in financial area, the drug molecular network in medical area, etc. Unlike grid-like data such as text, speech, and image, which can be easily embedded into a Euclidean space and naturally fit to the existing deep learning frameworks, graph is a non-European data and can not directly apply to existing deep learning models. Thus, it is necessary to specially design the graph-oriented neural network frameworks for graph learning.
Graph learning algorithms like graph neural networks (GNN) combine end-to-end learning with inductive reasoning and are very likely to solve the problems that current deep learning frameworks cannot handle, such as relation reasoning, interpretability, etc. The representation, computation, and generalization of structural knowledge in graph learning are the key to achieving human-like AI.
Euler is a large-scale distributed graph learning system. It can work with deep learning tools like TensorFlow or X-Deep Learning and support users to train models on very complex heterogeneous graphs with billions of nodes and tens of billions of edges. The core capabilities of Euler system are as follows:
- Large-scale distributed graph learning. In industry, the real graph often contains billions of nodes and tens of billions of edges. It is infeasible to carry out single-machine training on such large-scale graphs. Euler allows graph segmenting and efficient and stable distributed training, and thus easily supports the very large-scale graph learning.
- Heterogeneous graph embedding. In most cases, the real-world graphs are very complex with multi-typed nodes and edges and rich side information, which makes it difficult for some recently-proposed graph neural networks to learn effective embeddings. Euler provides heterogeneous operators for graph structure storage and graph computation and side information learning, and thus perfectly supports the embedding learning on heterogeneous graphs.
- Combination of graph learning and deep learning. Deep learning has proven to be useful in many industrial applications, such as search, recommendation, advertising, etc. It is desirable to augment the model performance by combining graph learning with deep learning. Euler supports mini-batch training based on deep learning samples and achieves jointly training by directly use the graph embeddings as the input to deep neural networks.
- Layered abstraction and flexible extensity. Euler system is abstracted to three layers: algorithm interface layer, graph operator layer, and graph engine layer. Based on the multi-layered abstraction, users can quickly develop a graph learning model on Euler system. In fact, Euler has already provided many built-in algorithms for everyone to use directly.
As shown in Figure 1, Euler system is abstracted to three layers: distributed graph engine layer, graph operator of Middle Tier, Built-in algorithm interface layer. We describe each layer in detail as follows.
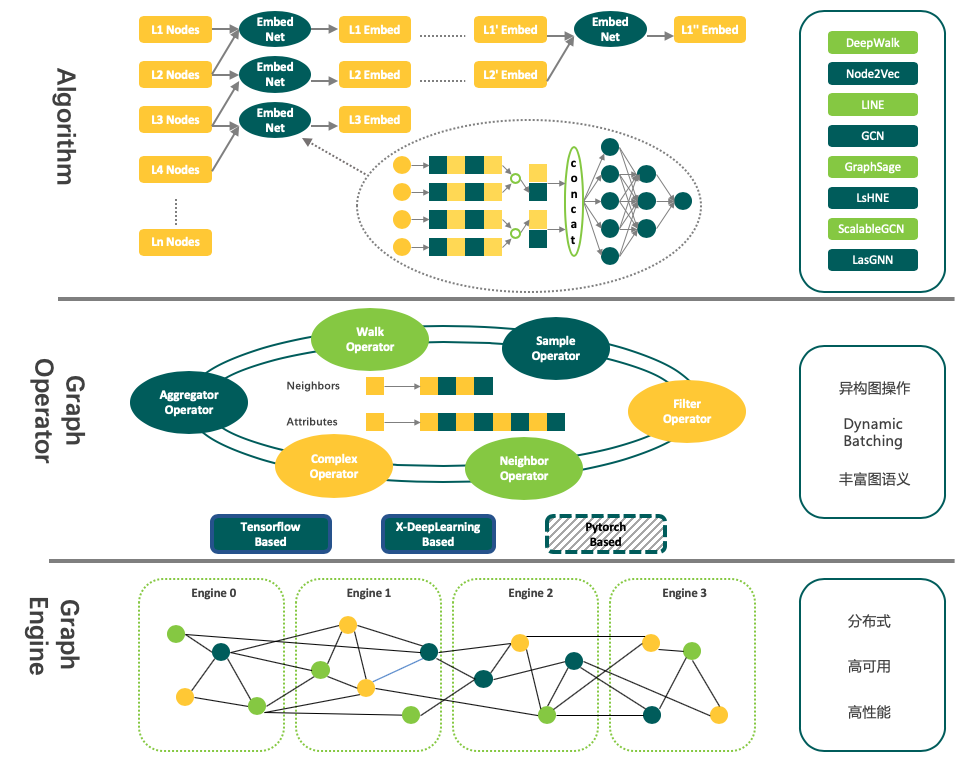
Figure 1 Euler architecture
To support our massive business, we must address the challenge of the very large-scale graph storage and computation, and the complexity of heterogeneous graphs with multi-typed nodes and edges and their attributes. Our distributed graph engine in Euler is optimized for large-scale graph storage, distributed parallel graph computation and heterogeneous graphs to ensure efficient and effective performance in industrial scenarios.
- To store large-scale graphs with billions of nodes and tens of billions of edges, Euler adopts distributed storage architecture. When a graph is loaded, it will be divided into multiple subgraphs inside the graph engine layer of Euler, and then each computation node will severally load one or several subgraphs.
- To make full use of the capability of each computation node, the operation for original graph is decomposed into multiple sub-graph operations performed by each node in parallel. In this way, with more nodes added, we will get better service capabilities. Moreover, Euler supports for multiple replicas. Therefore, users can flexibly balance the number of shards and replicas to achieve better service capabilities. We also optimize the graph storage structure and graph operations for graph embedding. As a result, the performance in single machine has been improved several times.
- It is essential for many complex business scenarios to handle heterogeneous graphs with multi-typed nodes and edges and attributes. To achieve heterogeneous graph computation, the underlying storage is organized according to different types of nodes and edges. Then, we can efficiently support heterogeneous graph operations.
Although we have built in many superior algorithms, it is not easy to satisfy all the needs of customers for the diversity of graph learning algorithms and the complexity of real-world business. Therefore, we design some flexible and powerful graph operators based on the underlying graph engine of Euler, and all of these operators support heterogeneous graph computation. Users can use them to quickly build own models to meet specific business requirements.
First, the distributed graph engine of Euler provides C++ API to support all graph operations. By leveraging the C++ API to visit graph engine, we can easily add graph operators based on a deep learning framework like TensorFlow or Alibaba's X-Deep Learning. The code released in this version are based on TensorFlow framework and we will extend to other deep learning frameworks like PyTorch in future work.
Thanks to the flexibility of graph operators, the deep learning framework can interact with Euler in each mini-batch, and dynamically expand and organize training samples. In this way, Euler not only supports the traditional graph-specific learning model, but can also incorporate the ability of graph learning into traditional learning tasks and achieve end-to-end training. We classify the provided graph operators into several categories as follows according to their capabilities.
- Global weighted sampling for nodes and edges. This is mainly used for randomly generating mini-batch samples and negative sampling.
- Neighbor operation for a given node. This is the core capability of graph computation, including weighted sampling of neighbors, top K weighted selecting of neighbors, etc.
- Nodes'/edges' attribute lookup. This allows a model to use richer side information rather than just ID features of nodes/edges.
Considering the facilitation for users and the usability of the framework, we have built in a bunch of state-of-the-art graph learning models and our internal superior algorithms. For all of them, we have conducted extensive tests to ensure the efficiency and effectiveness. The performances of open-released models are aligned with the results in their original papers. Users can directly load their own data to Euler syetem to use these built-in algorithms without any development work. For details of the built-in algorithms, please see the paper links in the table below.
Note that the LsHNE model and LasGNN model are specifically designed for complex heterogeneous graphs and have been widely applied to many real business in Alibaba. We also extract the rich heterogeneous data in Alibaba and open it for researchers. You can download the data in here.
| Name | Algorithm Type | In House | Description |
|---|---|---|---|
| DeepWalk | random walk | no | Unsupervised algorithm with unbiased random walk. |
| Node2Vec | random walk | no | Deploying a biased-random walk to balance the breadth-first (BFS) and depth-first (DFS) graph searches. |
| LINE | other | no | Unsupervised algorithm preserving 1st-order and 2nd-order proximities. |
| GCN | neighbor aggragation | no | Semi-supervised algorithm which defines a convolution operator to directly operate graph-structured data. |
| GraphSAGE | neighbor aggragation | no | Generalized model from GCN by introducing neighbor sampling and aggragation. |
| GAT | neighbor aggragation | no | Graph neural network model which operates graph-structured data by leveraging masked self-attentional layers. |
| LsHNE | random walk | yes | Random walk in heterogeneous graphs |
| LasGNN | neighbor aggragation | yes | Semi-supervised large-scale heterogeneous graph convolutional network learning method. |
| Scalable-GCN | neighbor aggragation | yes | A method to accelerate GCN training. |